Электротехника. 06 Лекция. Электрические цепи однофазного синусоидального тока. Синусоидальный ток и основные характеристики
 Скачать 111 Kb.
|
|
Электрические цепи однофазного синусоидального тока. §1. Синусоидальный ток и основные характеристики. Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону.  (1)Максимальное значение тока называют амплитудой, обозначим её  ,  - п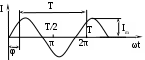ериод колебаний, - это время, за которое совершается одно полное колебание.Ч  астота равна числу колебаний за 1 секунду. Частоту  измеряют в герцах (Гц), угловая частота это: её измеряют в Радиан/сек или с-1. Аргумент синуса, т.е.  называют фазой.Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой (Im); угловой частотой (ω); начальной фазой (φ). В РФ и Европе в электросети частота 50 Гц, а в США – 60 Гц. §2. Среднее действующее значение синусоидально изменяющейся величины. Под средним значением синусоидально изменяющейся величины понимают её среднее значение за полпериода. Среднее значение тока:  Аналогично:  . .Обычно используется понятие действующего значения синусоидально изменяющейся величины (его называют эффективным или среднеквадратичным). Действующее значение тока: 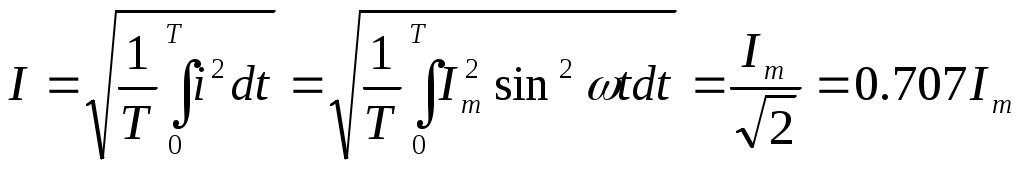 Аналогично действующее значение ЭДС и напряжения:  и  .Действующее значение синусоидального тока I численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток. Количество теплоты, выделенное за один период синусоидального тока:  .Тепло, выделенное за это же время постоянным током, равно:  , тогда или  ;Большинство измерительных приборов показывают действующее значение измеряемой величины. §3. Представление синусоидальных функций в виде комплексных переменных. Л 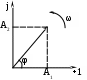 юбое комплексное число имеет действительную (Re) и мнимую (Im) часть и может быть представлено графически: по оси абсцисс (оси Х (+1)) откладывают действительную часть, по оси ординат (оси Y (j)) – мнимую часть  .Формула Эйлера:   , гдеА – называют модулем (длиной) вектора. Алгебраическая форма:  . ;  Положительным направлением вращения вектора А считается вращение против часовой стрелки. Для упрощения принято на комплексной плоскости изображать вектора синусоидально изменяющихся величин для момента времени  . Тогда вектор  равен: ,где  - комплексная величина, модуль которой равен  , а угол, под которым вектор проведён к оси +1 на комплексной плоскости, равен начальной фазе φ. Обозначим действительную часть  : и мнимую:  .Таким образом, синусоидально изменяющийся ток i(1) может быть представлен:  Величину называют комплексной амплитудой тока i(1). Комплексная амплитуда изображает ток i на комплексной плоскости для момента времени ωt=0.Рассмотрим 2 примера на переход от мгновенного значения тока i(1) к комплексной амплитуде и от комплексной амплитуды к мгновенному значению. Пример 1. Ток  . Тогда  , а  .Пример 2. Комплексная амплитуда тока  , тогда мгновенное значение тока равно: Под комплексным действующим значением тока 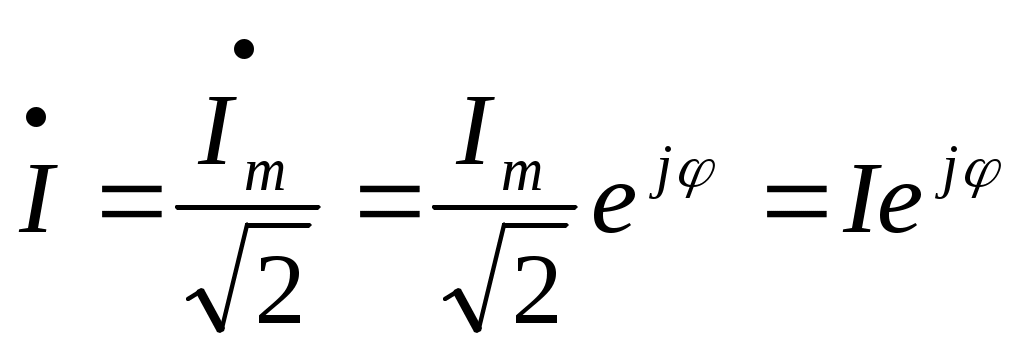 понимают величину: .Пример 3. Записать выражение комплексного действующего значения тока для примера 1.  |