1. Комплексное число в алгебраической форме записи.
Комплексным числом в алгебраической форме записи называется выражение вида z=a+ib , где а и b вещественные числа, I – мнимая единица, равная по определению i= 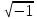 , , 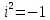 , a,b ϵ R. а – вещественная часть комплексного числа, b – мнимая часть компл. числа. Принято записывать мнимую часть комплексного числа как b=Im(z), а действительную а=Re(z) , a,b ϵ R. а – вещественная часть комплексного числа, b – мнимая часть компл. числа. Принято записывать мнимую часть комплексного числа как b=Im(z), а действительную а=Re(z)
z=a+ib и z=a-ib – сопряжённые
Два комплексных числа z1=a1+ib1, z2=a2+ib2 равны друг другу, когда равны их мнимые и вещественные части z1=z2, когда a1=a2, b1=b2
|
10. Методы интегрирования (Интегрирование по частям).
Рассмотрим произведение 2х функций u=u(x) и v=v(x). Возьмем дифференциал произведения: d(u*v)=vdu+udv ∫𝑢𝑑𝑣=𝑢𝑣−∫𝑣𝑑𝑢. Здесь| du=u’dx, v=∫𝑑𝑣|
Выделяют основные 3 типа интеграла, берущихся по частям:
1. Под знаком интегралла многочлен
Pn(x)= e^x, a^kx, cos(kx), sin(kx)
здесь за u берем Pn(x),
а dv= e^kx, a^kx, cos(kx), sin(kx)
2. Pn(x)=ln(x), arctg x, arccos x, arcsin x, arcctg x. Здесь за u берем: ln(x), arctg x, arccos x,arcsin x, arcctg x
а за dv берем все остальное, то есть Pn(x) dx
3. У нас даны две функции, одну из функций берем за u, другую за dv.
Основное правило выбора u и dv:
За u принимается та часть функции, кот. при дифференцировании упрощается, а за dv та часть подынтегрального выражения, которая легко интегрируется.
|
Интегрирование тригонометрических функций.
Универсальная подстановка:
t=tg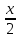
Универсальная подстановка для вида:
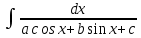
t=tg 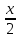
sin x= 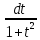
cos x= 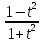
dx= 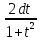
|
2. Геометрическое изображение комплексного числа.
Каждому компл. числу z=a+ib можно поставить в соответствии точку на плоскости М(a,b).
П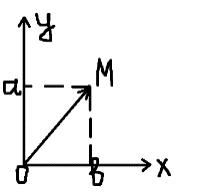 ри этом ось ОХ наз-ся вещественной, ОУ-мнимой. При изображении к.ч. на пл-ти ХОУ на пл-ти ставится знак z и пл-ть наз-ся пл-тью комплексного переменного. ри этом ось ОХ наз-ся вещественной, ОУ-мнимой. При изображении к.ч. на пл-ти ХОУ на пл-ти ставится знак z и пл-ть наз-ся пл-тью комплексного переменного.
Иногда бывает удобно изображать не в виде точки, а в виде радиус-вектора.
|
47. Задачи, приводящие к тройному интегралу.
Пусть дано тело в пространстве объема V с непрерывно распределенной плотностью: ƍ=ƍ(x,y,z). Поставим задачу найти массу этого тела.
Разобьем его произвольно на части с объемами ΔVi . в каждой из этих частей выберем произвольную точку Pi(xi,yi) и будем считать, что в данной конкретной части тела плотность постоянна и равна значению плотности в этой точке:ƍi=ƍ(xi,yi,zi).
Тогда массу каждого такого участка приближенно можно сосчитать:mi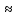 ƍ(xi,yi,zi)*ΔVi. ƍ(xi,yi,zi)*ΔVi.
Тогда масса всего тело приблизительно равна сумме этих произведений:
m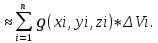
Чем больше n, тем точнее вычисления. Поэтому за точнее значение массы берут:
M= 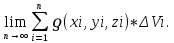
|
Интегрирование функций линейного аргумента.
Пусть F(x) - первообразная для функции f(x), то есть
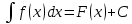 , тогда , тогда
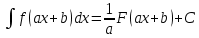 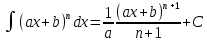 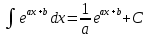
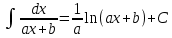
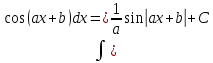 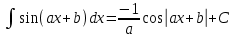
|
3. Показательная и тригонометрическая формы комплексного числа.
Возьмём на плоскости точку М(a,b), введём полярную систему координат совместив полярную ось с осью ОХ, а полюс с началом координат, тогда точка М будет иметь полярные координаты М(ϕ,r)
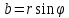 , , 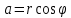 , ,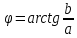 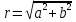 , , 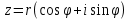 – тригонометрическая форма, r – полярный радиус точки М (модуль комплексного числа), ϕ – его аргумент. – тригонометрическая форма, r – полярный радиус точки М (модуль комплексного числа), ϕ – его аргумент. 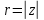
Применяя формулу Эйлера:
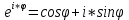
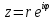 – показательная форма. – показательная форма.
|
8. Основные свойства неопр.интеграла.
1) Пост.множитель выносится за знак интеграла
2) Неопр. Интеграл алгеб.суммы конечного числа функций равен алгеб.сумме неопр.интегралов
3) Дифференциал от неопр.интеграла равен подинтегральному выражению
4) Производная неопр.интеграла равна подинтегральной функции
|
7.Таблица неопределенных интегралов:
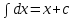 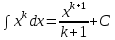
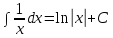 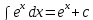
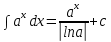 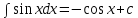 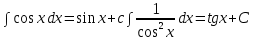
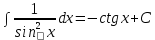 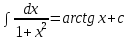
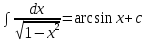 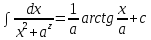
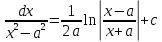 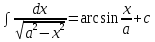
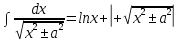 +c +c 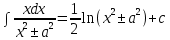
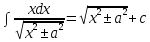 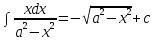
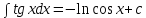 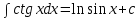
|
5. Действие над к.ч. (Возведение в степень, извлечение корня). Для того чтобы возвести компл. число в целую полож. степень n используют бином Ньютона. 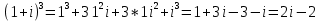
Для возведения в степень удобно использовать тригонометр. и показат. формы
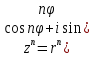 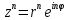
Извлечение корня. n – целое полож. число, nϵN Формула Мавра 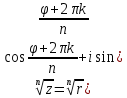 , k=0,1,2,…,n-1 , k=0,1,2,…,n-1
|
9. Методы интегрирования (Интегрирование разложением, метод замены)
С помощью свойств неопределенного интеграла и таблицы интегралов от элементарных функций становится возможным отыскание первообразных для несложных алгебраических выражений.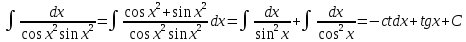
Метод замены. Часто удается упростить вычисление неопр.интеграла введнием новой переменной t, x=φ(t), dx=dφ(t)=φ’(t)dt
∫𝑓(𝑥)𝑑𝑥=∫𝑓(𝜑(𝑡))=𝜑′(𝑡)𝑑𝑡
Часто эту формулу используют в обратном направлении. Если под знаком интеграла есть сложная функция и как множитель производной её аргумента, то удобно вводить замену, заменяя новой переменной значение аргумента: ∫𝑓(𝜑(𝑥))∗𝜑′(𝑥)𝑑𝑥=|𝑡=𝜑(𝑥),𝑑𝑡=𝜑′(𝑥)𝑑𝑥|=
∫𝑓(𝑡)𝑑𝑡
|
13. Разложение правильной рациональной дроби на сумму простейших. 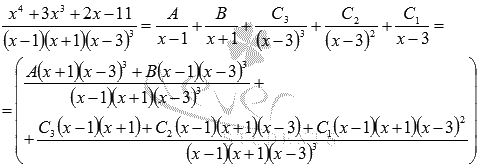
Расписываем числители через коэф A,B и С
Выписываем равенство числителей изначальной дроби и той, что состоит из коэф.
Находим A,B и С
Подставляем их и вычисляем интеграл
|
28. Дифференциальные уравнения 1 порядка. Общие понятия. Определение: Диф. Уравнением называется равенство связывающим независимую переменную, неизвестную функцию от этой переменной и её производные или диференциалы. Диф. уравнения разделят по следующим категориям: 1) По порядкам (порядком диф. ур. называется порядок входящей в него старшей производной) 2) Диф. ур. могут быть линейными и нелинейными. В лин. диф. ур. функция и её производная входят в 1 степень и не умножаются друг на друга. 3) Уравнения могут быть обыкновенными и в частных производных. Если неизвестная функция зависит от 1 переменной, то обыкновенная, если от нескольких – то частная производная. Определение: Диф. ур. 1 порядка называется равенство, связывающее независимую переменную х, неизвестную функцию от этой переменной y и её 1 производную. В общем виде F(x,y,y’)=0. Если из уравнения можно выразить y’=f(x,y), то ур. называется разрешённым относительно 1 производной. Часто ур. 1 порядка записывают в виде P(x,y)dx+Q(x,y)dy=0. Решить диф. ур это значит найти функцию y=ϕ(x) при подставлении которого в уравнение получается истинное равенство
|
29. Дифференциальные уравнения 1 порядка с разделяющимися переменными. Если решение диф. уравнения неоднозначно и может содержать различные постоянные y=f(x,c), c=const, то его называют общим. Одним из простейших видов дифференциальных уравнений является дифференциальное уравнение первого порядка, не содержащее искомой функции: y’=f(x) 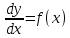 dy=f(x)dx dy=f(x)dx 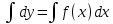 y=F(x)+C Решением содержащим С называется общим решением, при подстановке вместо С числа получаем частное решение. На практике для нахождения частного решения задают так называемое начальное условие y(x0)=y0. Теорема о существовании и единстве решения. y=F(x)+C Решением содержащим С называется общим решением, при подстановке вместо С числа получаем частное решение. На практике для нахождения частного решения задают так называемое начальное условие y(x0)=y0. Теорема о существовании и единстве решения.
Пусть функция f(x,y) и её частная производная по y определена и непрерывная в некоторой области G изменяя переменные х и у, тогда какова бы не была (x0,y)ϵG существует единственное решение y=ϕ(x) удовлетворяющего условию ϕ(x0)=y0
|
51. Тройной интеграл в цилиндрических координатах.
Положение точки в пространстве можно задавать с помощью цилиндрических координат P(r,ϕ, z), где z-аппликата точки Р, r,ϕ-полярные координаты точки P’, кот. Яв-ся проекцией точки Р на пл-ть ХОУ.
Если проекция Ω на пл-ть ХОУ в область Д имеет границы, кот-ые удобно задавать в полярных координатах r=r1(ϕ) r=r2(ϕ)
Φ=α ϕ=β, то тройной интеграл в фоормуле 5 удобно переписать:
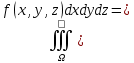
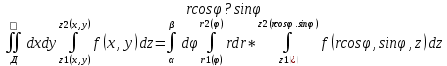 (6) (6)
Тройной интеграл от единицы численно равен объему области:
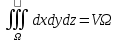
|
4. Действие над к.ч. (сложение, умножение, дедение)
1) Суммой двух компл. чисел называется компл. число, которое получается по правилу складываются отдельно вещественные, отдельно мнимые части. z1+z2=(a1+a2)+i(b1+b2)
2) Разностью 2-х компл. чисел z1 и z2 называется компл. число, которое получается по правилу вычитаются отдельно вещественные, отдельно мнимые части.
z1-z2=(a1-a2)+i(b1-b2)
3) Произведением двух компл. чисел называется компл. число, которое получается по правилу умножения многочленов, причём i^2=-1
z1*z2=(a1+ib1)(a2+ib2) Замечание i^3=-i, i^4=1, i^4k=1, i^(4k+1)=i, i^(4k+2)=-1, i^(4k+3)=-i. Если комп. числа заданы в тригонометрической форме, то z1z2=r1r2(cos(ϕ1+ϕ2)+isin(ϕ1+ϕ2)), если в показательной, то z1z2=r1r2e^(i(φ1+φ2))
4) Частным от деления двух компл. чисел называется компл. число, которое получается по правилу z1/z2=(a1+ib1)/(a2+ib2)=((a1+ib1)(a2-ib2))/((a2+ib2)(a2-ib2))
Если числа заданы в тригон. Или показат. формах, то их модули деляться, а аргументы вычитаются
z1/z2=r1/r2(cos(ϕ1-ϕ2)+isin(ϕ1-ϕ2)) z1/z2=r1/r2 e^(i(φ1-φ2))
|
6. Понятие первообразной и неопределенный интеграл. Геометрический смысл.
Процесс отыскания функции по её известной производной или дифференциалу наз-ся интегрированием, а сама функция наз-ся первообразной.
f(x)=(F(x))’ fxdx=dF(x)
Теорема
Пусть F(X)-первообразная для функции f(x). Тогда любая другая первообразная этой функции Ф(х) будет отличаться от F(x) на постоянное слагаемое:
Ф(x)=F(x)+qC, C-const.
Множество всех первообразных функции f(x) наз-ся её неопределенным интегралом и обозначается: ∫𝑓(𝑥)𝑑𝑥=𝐹(𝑥)+𝐶
Здесь ∫– знак неопр. Интеграла, f(х)- подинтегральная функция, f(x)dx-подинтегральное выражение. Процесс нахождения функции по её известной производной называется интегрированием.
Геометрическая интерпретация неопр.интеграла или его физ.смысл.
Геометрически неопр.интеграл представляет собой семейство кривых с уравнениями y=F(x)+C, которые получается друг из друга путем сдвига кривых вдоль оси ОУ:
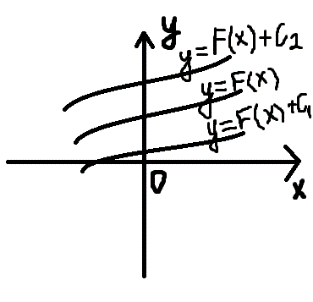
|
Интегрирование простейших рациональных дробей.
Рациональной дробью наз-ся частное от деления 2х многочленов.
Если степень числителя больше или равно степени знаменателя, рац. дробь-неправильная.
если наоборот-правильная.
Всякую неправильную рац.дробь можно предстваить в виде суммы многочлена и правильной рац.дроби:
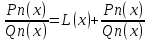
Таким образом, интегрирование неправильной рац.дроби сводится к делению многочлена и правильной рац.дроби.
Всякую правильную рац.дробь можно представить в виде суммы конечного числа правильных рац.дробей след. 4х типов:
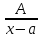 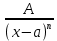
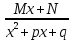 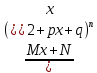
Общие схемы интегрирования рац.дробей:
Если дробь неправильная, выделить целую часть
Разложить прав.рац.дробь на сумму простейших
Найти неопр. Коэффициенты
Проинтегрировать получившиеся простейшие дроби
|
25. Геометрическое приложение определённого интеграла (вычисление объёма тела вращения). Телом вращения вокруг оси Ох называется фигура, полученная от вращения вокруг оси Ox криволинейной трапеции, ограниченной графиком непрерывной на отрезке [a,b] кривой y=f(x) и прямыми y=0,x=a и x=b
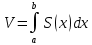 , хϵ[a,b] – поперечное сечение – круг с радиусом r=f(x), площадь круга – S(x)=Пr2=П(f(x))2 , хϵ[a,b] – поперечное сечение – круг с радиусом r=f(x), площадь круга – S(x)=Пr2=П(f(x))2 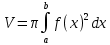
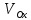 = =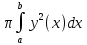
Телом вращения вокруг оси Oyназывается фигура, полученная от вращения вокруг оси Oy криволинейной трапеции, ограниченной графиком непрерывной на отрезке [a,b] кривой y=f(x) и прямыми х=0,y=c и y=d 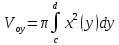
|
26. Геометрическое приложение определённого интеграла (вычисление длины дуги).
Ломаная, которая приблизительно заменяет нашу дугу AB длина дуги приблизительно будет равна 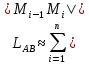 Если в дугу можно вписать ломаную, то её называют спрямляемой. Если в дугу можно вписать ломаную, то её называют спрямляемой.
Теорема. Пусть дана плоская прямая AB уравнение которой задаётся функцией y=f(x) точками A(a,f(a)), B(b,f(b)), функция f(x) и её производная определены и непрерывны на отрезке [A,B], тогда длина дуги вычисляется по формуле 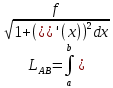
Д-во: Разбиваем дугу на n частей с точками M0, M1…Mn. Mi(xi, f(xi)), xiϵ[a,b] Каждую из маленьких дуг Mi-1, Mi заменим отрезками [Mi-1, Mi]. Длина каждого этого отрезка будет вычисляться 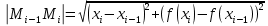
По теореме Логранжа: f(xi)- f(xi-1)=f’(Ci)( xi-xi-1), nϵ[xi-1,xi]. 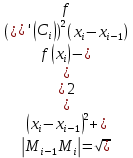
Длина дуги AB 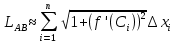
Чем меньше n, тем точнее вычисления: 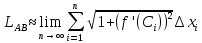 , , 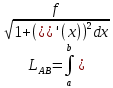
|
27. Несобственный интеграл.
1) Пусть функция f(x) определена и непрерывна на [a;+∞), 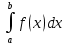 , bϵ[a;+∞) Если существует конечный предел такого интеграла при b→∞, то этот предел называется несобственным пределом 1 рода с бесконечной верхней границей , bϵ[a;+∞) Если существует конечный предел такого интеграла при b→∞, то этот предел называется несобственным пределом 1 рода с бесконечной верхней границей 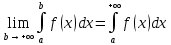 Аналогично можно определить интеграл с бесконечной нижней границей Аналогично можно определить интеграл с бесконечной нижней границей 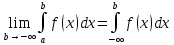 Несобственный интеграл с бесконечными верхней и нижней границами определяется как сумма интегралов Несобственный интеграл с бесконечными верхней и нижней границами определяется как сумма интегралов 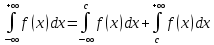 Такой интеграл существует, если существуют оба слагаемых интеграла. Если несобственный интеграл равен конечному числу, говорят, что он сходится, если не конечному, то рассходится. Такой интеграл существует, если существуют оба слагаемых интеграла. Если несобственный интеграл равен конечному числу, говорят, что он сходится, если не конечному, то рассходится.
2) Пусть функция f(x) определена и непрерывна на [a;b], но в точке сϵ[a;b] имеет разрыв, тогда 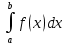 называется несобственным интегралом 2 рода. Он представляет собой сумму двух пределов называется несобственным интегралом 2 рода. Он представляет собой сумму двух пределов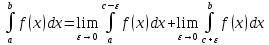
| |
 Скачать 152.53 Kb.
Скачать 152.53 Kb.