|
|
шпора 2 курс выш мат. 1. Комплексное число в алгебраической форме записи
Вычисление двойного интеграла В п\у координатах.
Область Д наз-ся правильным в направлении оси ОУ, если прямая, проходящая через внутренние точки этой области параллельная оси ОУ, пересекает её границу равно в 2х точках.
Границу такой области записывают уравнением:
y=ϕ1(x), y=ϕ2(x) (ϕ1(x)⩽ϕ2(x))
x=a, x=b(a
В таком случае дв.интеграл вычисляется по ф-ле:
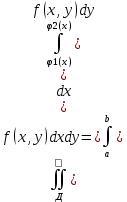 (5) (5)
Здесь 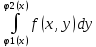 –внут.интеграл вычисляется в первую очередь. Переменная х считается постоянной. –внут.интеграл вычисляется в первую очередь. Переменная х считается постоянной.
Результатом яв-ся ф. F(x).
Далее вычисляется внешний интеграл от этой ф. 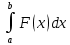 . .
Результатом дв. Ин. Яв-ся число.
Пределы во внут.интеграле зависят от переменных внешнего интеграла.
Пределы во внешнем интеграле всегда постоянны.
Область Д наз-ся правильным в направлении оси ОХ, если прямая, проходящая через внутренние точки этой области параллельная оси ОХ, пересекает её границу равно в 2х точках.
Границу такой области записывают уравнением:
х=Ψ1(у), х=Ψ2(у) (Ψ1(у)⩽Ψ2(у))
у=с, у=d (с
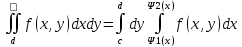
Здесь внут.интеграл считается по х, при его вычислении у=const. результатом его вычисления яв-ся ф. F(y), кот. идет во внешний интеграл как подынтегральная ф.
Замечание : в более сложных случаях область надо делить на правильные части.
Двойной интеграл в полярных координатах.
Рассм. Интеграл 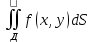 . Так как разбиение области Д на части проводится произвольно, применим след.подход. . Так как разбиение области Д на части проводится произвольно, применим след.подход.
Совместим начало коор-т с полюсом полярной системы координат, а полярную ось с осью ОХ.
Разбиение области Д будем проводить лучами, выходящими из точки О и составляющими друг с другом Δϕi, i=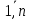 и окружностями с центром в точке О и радиусами ri , i= и окружностями с центром в точке О и радиусами ri , i=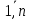 . .
Рассм. Один из получившихся произвольных участков.
Он образовна двумя лучами составляющие угол Δϕi и 2 окружностями с радиусами ri и 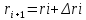 . Площадь этого участка можно найти как разность секторов: . Площадь этого участка можно найти как разность секторов:
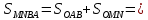
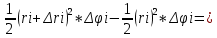 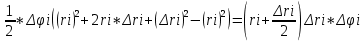
Проведем окружность с 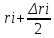 . .
Тогда площадь нашего участка, которую м. обозначит за ΔSi:
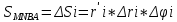
Возьмем на новой окр.произвольную точку Р(xi,yi). Её полярный радиус ri, а полярный угол обозначим за ϕi.
Используем связь между п\у и полярными координатами:
Xi=r’i*cosϕi
Yi=r’i*sinϕi
Тогда дв.интеграл от ф. f(x,y) по области Д можно записать:
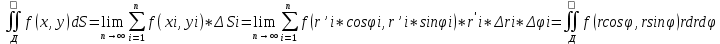 (7) (7)
Пусть область Д имеет границу, кот. Определяется ур-ниями в полярных координатах:
r=r1(ϕ) r=r2(ϕ) ( r1(ϕ) ⩽ r=r2(ϕ) )
ϕ=α ϕ=β (α<β)
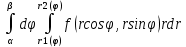 (8) (8)
Угол отсчитывается от оси против часовой стрелки.
Замечание 1.
Если начало координат лежит внутри области интегрирования то формула 8 примет вид:
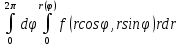
Замечание 2.
Если начало координат лежит на границе области интегрирования, то фоомула 8 примет вид:
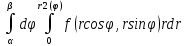
|
Приложения двойного интеграла.
Площадь ограниченная замкнутой областью Д на пл-ти ХОУвычисляется по формуле:
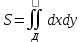
Объем области ограниченной сверху поверхностью z=f(x,y) , снизу замкнутой областью Д, а по бокам -цилиндрической поверхностью, образующие которой параллельны OZ, а направляющие яв-ся областью Д, вычисляется по формуле:
V=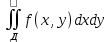
Замечание .
Если тело ограничено снизу поверхностью z=ϕ(x, y), но проецируется на пл-ть ХОУ как область Д то его объем равен:
V=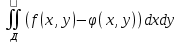
Площадь поверхности в пространстве
Пусть в пространстве дана поверхность z=f(x,y), кот.проецируется в ограниченную замкнутую область Д.
Пусть ф. f(x,y) и её частные производные 1го порядка 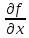 , , 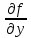 непрерывны в каждой точке области Д. непрерывны в каждой точке области Д.
Тогда площадь:
S=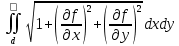 . .
Координаты центра тяжести плоской пластины.
Статистическим моментом относительно OХ мат.т., имеющая массу m, наз-ют произведение её ординаты на массу.
Ix=y*m
Статистическим моментом относительно OY мат.т., имеющая массу m, наз-ют произведение её абциссы на массу.
Iy=x*m
Если тело состоит из нескольких точек, то за её статистический момент принимают сумму моментов всех точек.тогда для ограниченной замкнутой области Д на ХОУ стат.момент равен:
Ix=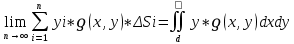
Iy=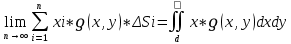
ƍ-ф., определяющая плотность области Д.
Координаты центра тяжести огран.замкнт.области Д определяются:
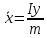 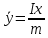 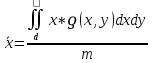
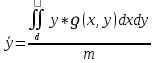
|
48. Определение тройного интеграла.
Пусть дана ограниченная замкнутая область Ω в пространстве, в каждой точке кот-ой определена и непрерывна ф. f(x,y,z)
Произведем след.действи:
Разобьем область произвольно на n частей с объемами 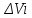 . В каждой из этих частей выберем произвольно точку Pi(xi,yi,zi), i= . В каждой из этих частей выберем произвольно точку Pi(xi,yi,zi), i=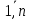 . И составим сумму вида: . И составим сумму вида: 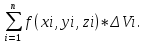 (1), которую будем наз-ть интег.суммой. рассм.предел суммы (1): (1), которую будем наз-ть интег.суммой. рассм.предел суммы (1):
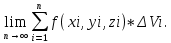 (2) (2)
Если сущ-ет конечный предел 2 интег.суммы 1, независящей ни от способа разбиения области на части, ни от выбора в них промежуточных точек, то
Тот предел наз-ся тройным интегралом от ф. f(x,y,z) по области Ω и обозначается:
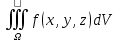 (3) (3)
Теорема о сущ-нии тройного интеграла.
Для всякой ф. f(x,y,z) непрерывной в огран.замкн.области Ω сущ-ет тройной интеграл по этой области.
Так как разбиение области на части производится произвольно, осуществимо это с помощью плоскостей параллельных координатнм плоскостям. Тогда каждая часть будем параллепипедом с измерениями: Δxi, Δyi, Δzi.
Тогда объем этой части равен ΔVi=Δxi*Δyi*Δzi
dV=dxdydz
тогда интеграл 3 перепишется в 4
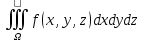
|
50. Вычисление тройных интегралов в п/у координатах.
Пространственная ограниченная замкнутая область Ω наз-ся правильной в направлении оси z, если выполняются след. Условия:
Прямая, проходящая через любую внут.т. области параллельно оси OZ пересекает границу области ровно в 2х точках
Область Ω проецируется на пл-ть ХОУ в правильную область Д
Любая из частей области Ω, отсеченная от неё пл-тями параллельными координатным, обладает 1м и 2м свойствами.
Область параллельная направлению OZ ограничена снизу z=z1(x,y), сверху-z=z2(x,y) и проецируется на ХОУ в правильную область Д
Тогда 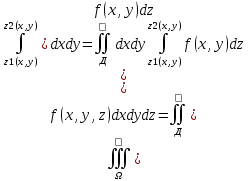
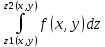 -внут.интеграл, вычисляется в первую очередь. При его вычислении х и у постоянны. Результатом вычисления яв-ся ф. F(x,y), кот. Идет во внешний интеграл. -внут.интеграл, вычисляется в первую очередь. При его вычислении х и у постоянны. Результатом вычисления яв-ся ф. F(x,y), кот. Идет во внешний интеграл.
Если область Д правильная в направлении оси У имеет границы y=ϕ1(x), y=ϕ2(x), x=a, x=b, то тогда вычисление тройного интеграла можно расписать по формуле:
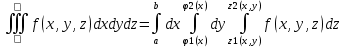 (5) (5)
|
49. Свойства тройного интеграла.
Постоянный множитель выносится за знак дв.ин.
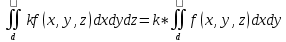 dz dz
Интеграл от алгеб.суммы равен алгеб.сумме 3-х интегралов:
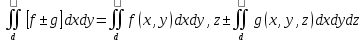
Если ф. f(x,y,z)⩾0 по области Д, то и 3 интеграл от этой ф. тоже
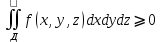 . .
Если ф. f(x,y,z) и φ(x,y,z) удовлетворяют неравенству f(x,y,z)⩾ φ(x,y,z) в области Ω, то и 3 интегралы удовлетворяют такому же неравенству
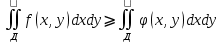
Если область Ω можно представить или разбить на конечное число частей, то 3 Интеграл от ф. f(x,y,z) можно представить как сумму 3-х интегралов по каждой из этих областей.
Ω=Ω1+Ω2+Ω3+…+Ωn
Теорема о среднем
Если функция f(x,у, z) определена и непрерывна в замкнутой ограниченной области Ω, то сущ-ет по крайней мере одна точка Р0(х0, у0, z0) в области Ω, что имеет место равенство:
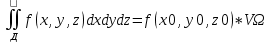
|
ДУ 2го порядка, допускающие понижение степени.
y’’=f(x) ( нет y, y’)
y’=p, y’’=p’
p’=f(x)
dp/dx=f(x)
dp=f(x)dx
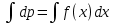
P=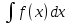
y’=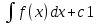
y=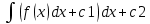
y’’=f(x, y’) (нет у)
y’=p y’’=p’
p’=f(x,p)
p=ϕ(x1, c1)
y’= ϕ(x1, c1)
dy/dx= ϕ(x1, c1)
dy= ϕ(x1, c1)dx
y=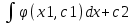
y’’=f(y, y’) (нет х)
y’=p, y’’=(p)’x=dp/dx=
y’=p, y’’=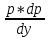
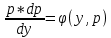
p=F(y1, c1)
y’=F(y, c1)
dy=F(y, c1)dx
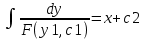
|
|
|
7.Таблица неопределенных интегралов:
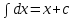
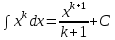
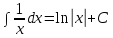
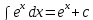
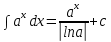
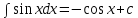
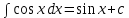
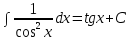
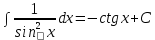
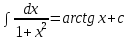
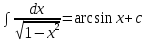
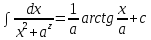
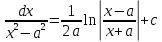
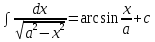
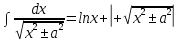 +c +c
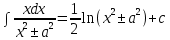
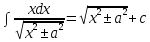
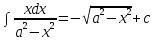
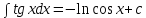
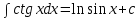
|
|
|
|
 Скачать 152.53 Kb.
Скачать 152.53 Kb.