шпора 2 курс выш мат. 1. Комплексное число в алгебраической форме записи
 Скачать 152.53 Kb. Скачать 152.53 Kb.
|
| Интегрирование иррациональных дробей. 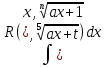 k-наименьшее общее кратное показателей всех корней ax+b= 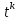 x= 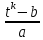 dx= 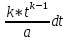 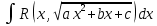 Под корнем выделяется полный квадрат и вводится замена, после чего получаются: 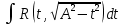 t=A sin t dt=A cosz dz 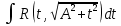 t=A*tg z dt= 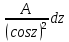 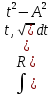 t= 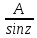 dt= 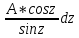 После всего получается рац.дробь. | Задачи, приводящие к понятию определенного интеграла. Задача о криволинейной трапеции. Криволинейной трапецией будем называтьфигуру, ограниченную сверху графиком функции y=f(x), по бокам прямыми x=a, x=b(a Разобьем отрезок ab на N частей x0, x1, x2, … , xn. a=xi, b=xn. Получим n криволинейных трапеций. На каждом из отрезков выберем произвольную точку Сi и построим прямоугольники с основаниями Δxi и вершинами f(Si). 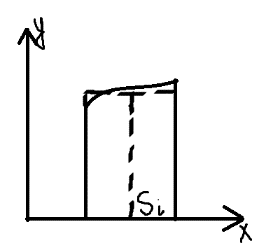 Такие прямоугольники заменяют маленькие криволинейные трапеции, а значит можно приближенно заменить: 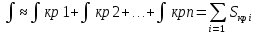 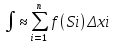 Чем больше N, тем точнее наши вычисления, поэтому для точного вычисления берут: 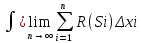 Задача о работе приближения. 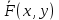 (зависит от её точки) (зависит от её точки)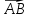 | Определение определенного интеграла. Путь функция f(x) определена на отрезке [a,b]. Выполним след.действия: Разобьем отрезок [a, b] в точках x0, x1, …, xn ( x0=a, xn=b) на n частей с длинами Δxi=xi- 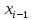 , i= , i=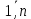 В каждом отрезке выберем произвольную точку 𝛏iϵ[ 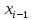 , ki], i= , ki], i=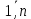 Составим сумму вида 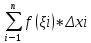 (1), которую будем называть интегральной суммой. (1), которую будем называть интегральной суммой. 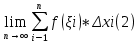 если существует конечный предел (2) при n→∞ интегральной суммы (1), независящий от способа разбиения отрезка [a,b] на части и выбора в них точек 𝝃i, то этот предел наз-ся определенным интегралом от функции f(x) по отрезку [a,b] и обозначается 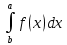 здесь a иb соот-но нижние и верхние пределы интегрирования, f(x) -подинтегральная функция, dx-переменная длины. Если функция f(x) больше 0 на отрезке [a,b] , то исходя из предыдущего пункта, определенный интеграл имеет простой геометрический смысл: это площадь криволинейной трапеции, ограниченной сверху графиком функции y= f(x), а по бокам и снизу прямыми x=a, x=b, y=0. Теорема о существовании определенного интеграла. Для всякой функции f(x) непрерывной на отрезке [a,b] существует определенный интеграл к этой функции. |
| Свойства определенного интеграла. Постоянный множитель выносится за скобки 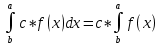 dx dxДокозательство: Рассмотрим функцию c*f(x) 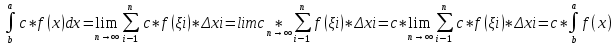 dx dxОпр.интеграл от суммы или разности конечного числа функции равен соот-но сумме или разности определенных интегралов этих слагаемых: 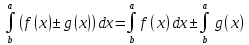 dx dxЕсли функция f(x) и g(x) удовлерворяют неравенству f(x)⩾g(x), то и определенные интеграла от этих функций тоже удовлетворяют этому неравенству: 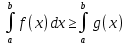 dx dxПусть m –наименьшее значение функции на отрезке [a,b], а M –наибольшая. Тогда имеет место неравенство: m(b-a)⩽ 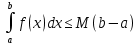 Пусть с-внутренняя точка отрезка [a,b], тогда 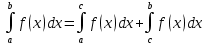 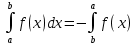 dx dxТеорема о среднем Пусть функция f(x) непрерывна на отрезке[a,b], тогда сущ-ет одна такая точка с на отрезке [a,b], что имеет место неравенство: 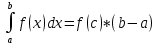 | 20. Замена переменной в определенном интеграле. Интегрирование заменой переменной. Рассмотрим интеграл 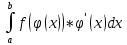 . . для нахождения первообразной подинтегральной функции нужно сделать замену t=φ(x) . определим область действия переменной t: φ(a)=α (t=φ(a)=α) φ(b)=β (t=φ(b)=β) при изменении переменной х от a до b переменная t не должна выходить за пределы [ α, β]. Тогда имеет место формула: 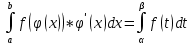 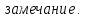 Замену в определенном интеграле можно рассмотреть по-другому: введем новую переменную t связанную со старой соотношением x=Ψ(t) a=Ψ(t) t1=α b=Ψ(t) t2=β требуем чтобы Ψ(t), Ψ’(t) были определены и непрерывны на отрезке [α, β] и чтобы при изменении х от a до b, tϵ [α, β]. В этом случае будем иметь фомулу: 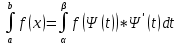 | 22. Вычисление площадей плоских фигур в прямоугольных координатах. Пусть дана фигура, ограниченная сверху куском кривой y=f(x), а слева, справа и снизу прямыми x=a, x=b, y=0. Площадь равна: S= 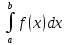  Если на [a,b] функция f(x)<0, мы получаем фигуру. 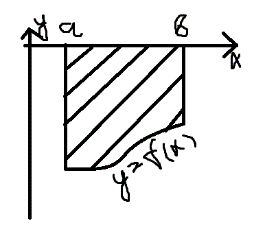 Тогда можно рассмотреть симметричную её фигуру, ограниченную сверху y=-f(x) S= 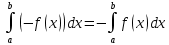 Все сказанное можно обобщить в формулу: 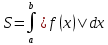 S= 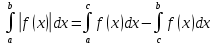 Sсс1дд1=Sавсд-Sавс1д1= 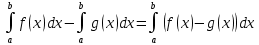 Замечание: Пусть уравнения, которыми ограничена фигура заданы x=φ(t), y=Ψ(t) И известны значения параметра t1=α, t2=β, соответствующие концам отрезка: x=a, x=b. S= 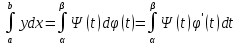 |
| Вычисление определенного интеграла. Формула ньютона-Лейбница. F(x)-одна из первообразных функции, тогда имеет место формула: 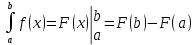 | 21. Интегрирование по частям. Рассмотрим произведение двух функций u=u(x), v=v(x) d(u*v)=vdu+udv проинтегрируем обе стороны по отрезку [a,b] 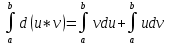  = =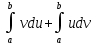 Выразим отсюда интеграл udv: 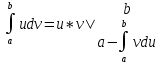 | 35. Структура общего решения ЛОДУ Теорема 2. Пусть у1 и у2-частные решения ЛОДУ 2го п. a0(x)y’’+a1(x)y’+a2(x)y=0 – составляют фунд.систему решений на некотором интервале. Тогда общее решение этого ур. будет иметь вид: у=с1у1+с2у2, с1 и с2=const. |
| Вычисление площадей в полярных координатах. Рассмотрим сектор, ограниченную лучами φ=α, φ=β, r=r(φ). Разобьем сектор на n частей лучами выходящими из полюса и составляющими с полярной осью углы φi. S=ΔSi Угловые меры маленьких секторов примем за Δφi. В каждом из этих секторов проведем луч, составляющий с полярной осью угол 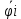 . Точка её пересечения с кривой r=r(φ) обозначим за Mi, и будем считать что в данном маленьком секторе радиус постоянный и равен . Точка её пересечения с кривой r=r(φ) обозначим за Mi, и будем считать что в данном маленьком секторе радиус постоянный и равенri=r( 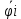 )=OMi )=OMiΔSi 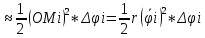 S 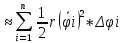 За точное значение площади сектора будем считать: S= 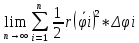 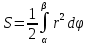 | Вычисление объемов тел по площади поперечных сечений. Объем тела по площади поперечного сечения. Рассмотрим тело в пространстве S=S(x), xϵ[a,b]. Разобьем отрезок [a,b] на n частей точками x0, x1, … , xn, x0=a, xn=b. В каждом из этих точек построим поперечное сечение тела. Объем тела будет равен сумме объемов маленьких сечений V=ΔVi. На каждом отрезке[ 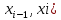 выберем точку 𝝃i и будем считать, что на данном участке площадь поперечного сечения постоянна и равна площади поперечного сечения в этой точке: выберем точку 𝝃i и будем считать, что на данном участке площадь поперечного сечения постоянна и равна площади поперечного сечения в этой точке:ΔVi’=S(𝝃i)Δxi, Δxi=xi- 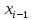 , ΔVi , ΔVi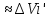 Значит объем нашего тела будет приближенно равен сумме таких объемов: V 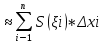 Чем больше xi, тем объем будет точнее. За точный объем тела берем: V= 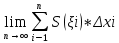 V= 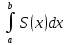 | Однородные ДУ 1-го порядка. Диф.уравнение 1-го порядка y’=f(x,y) наз-ся однородным, если его можно привести к виду: y’=ϕ 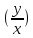 Однородное ур. Сводится к уравнению с разделяющимися переменными с заменой y/x =t  y=t*x y=t*x y’=t’x+tx’ y’=t’x+t t’x+t=ϕ(t) t’x=ϕ(t)-t t’=dt/dx 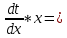 ϕ(t)-t ϕ(t)-tx*dt=( ϕ(t)-t) dx 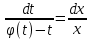 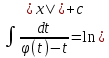 |
| Линейные ДУ 1-го порядка. Уравнения Бернулли. Диф.уравнение 1-го порядка наз-ся линейным, если его можно привести к виду: y’+f(x)*y=ϕ(x) если ϕ(x) 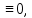 то уравнение имеет вид: то уравнение имеет вид:y’+f(x)*y=0 оно наз-ся линейным однородным и яв-ся уравнением с разделяющимися переменными. Если ϕ(x) 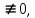 ур-ние наз-ся линейным неоднородным. Один из методов его решения-метод Бернулли. ур-ние наз-ся линейным неоднородным. Один из методов его решения-метод Бернулли.Метод Бернулли. Рассмотрим уравнение y’+f(x)*y=ϕ(x) Будем искать неизвестную функцию y=u*v, u,v- неизвестные ф. от х. Тогда y’=u’v+uv’ Подставим в наше уравнение эти выражения: u’v+uv’+f(x)*u*v=ϕ(x) последние 2 слагаемых слева выделяем и общий множитель выносим: u’v+u*(v’+f(x)*v)=ϕ(x) выражение в скобках приравниваем к 0: v’+f(x)*v=0 мы получили уравнение с разделяющимися переменными. Функция v=v(x) будем искать частным решения с=0. u’*v(x)=ϕ(x) – получили еще одно ур. с раздл. переменными. u=u(x)+с Тогда y=(u(x)+c)*v(x). Уравнение Бернулли. Диф.ур. 1-го порядка наз-ся ур.Бернулли, если его м. привести к виду: Y’+f(x)*y=ϕ(x)* 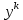 , k-рациональное число. , k-рациональное число.Ур. Решается методом Бернулли. | ЛНДУ 2го порядка. Рассм. Ур. a0(x)y’’+a1(x)y’+a2(x)y=b(x) Y’’+p(x)y’+q(x)y=f(x) (*) Теорема . Общее решение ур. (*) будет иметь вид у=у*+ 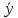 , где у*-общее решение, соответствующего однород.ур. y’’+py’+qy=0; а , где у*-общее решение, соответствующего однород.ур. y’’+py’+qy=0; а 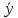 -частное решение неоднор.ур. (*). -частное решение неоднор.ур. (*).Докозательство : Пусть у*-общее реш. Однор.ур. y*’’+y*’+qy*=0 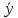 -частное реш. Неодн.ур. -частное реш. Неодн.ур.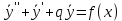 y=y*+ 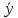 покажем что это сумма решений, для этого подставим вместо у: (y*+ 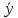 )’’+( y*+ )’’+( y*+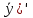 +q(y*+ +q(y*+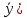 =f(x) =f(x)y*’’+ 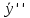 + y*’+ + y*’+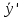 +q y*+ +q y*+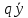 =f(x) =f(x)(y*’’+y*’+qy*)+( 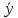 ’’+ ’’+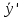 +q +q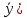 =f(x) =f(x)y*’’+y*’+qy*=0 → 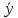 ’’+ ’’+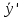 +q +q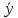 =f(x)→ =f(x)→ f(x)=f(x) |
