шпора 2 курс выш мат. 1. Комплексное число в алгебраической форме записи
 Скачать 152.53 Kb. Скачать 152.53 Kb.
|
|
38. Метод подбора частного решения. (ЛНДУ) ЛНДУ с ПК с правой частью спец.вида. Рассм. Ур. у’’+py’+qy=f(x) Его реш. Ищется в виде у=у*+ 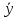 Если f(x)-спец. Вида, то 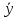 можно подобрать по f(x)/ можно подобрать по f(x)/Здесь возможны след.случаи: f(x)=Pn(x), тогда 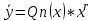 где Qn(x)-многочлен той же степени что и Pn(x), но с неопр.коэф. r-кратность корня в харак.ур. (=0,1,2) подставляя в ур. вместо y, y’, y’’ 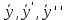 , сравнивая левую и правую части, находим неопр.коэф. , сравнивая левую и правую части, находим неопр.коэф.f(x)=Pn(x)* 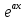 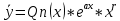 где Qn(x)-многочлен той же степени что и Pn(x), но с неопр.коэф. r-кратность корня k=a в харак.ур. (=0,1,2) f(x)= 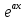 (Mcosβx+Nsinβx) (Mcosβx+Nsinβx)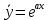 (Acosβx+Bsinβx)* (Acosβx+Bsinβx)*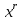 A, B-неопр.коэф. r-кратность корня k=a+ib в харак.ур. (=0,1) | ||
| 32. Определение дифференциального уравнения второго Диф урав 2-го порядка наз-ся равенство, которое связывает независимую переменную х, неизвестную ф. от этой переменной у и его первую и вторую производные. F(x,y,y’,y’’)=0 В ур-нии могут отсутствовать x, y, y’ , но y’’ должно быть обязательно. Если ур. М. представить в виде y’’=f(x, y, y’), то оно наз-ся разрешенным отн-но 2й производной. Для ур. 2го порядка также сущ-ют частные и общие решения. Рассмотрим y’’=2. Введем замену y’=u. Y’’=(y’)’=u’→ u’=2- это ур. С раздл.перем. du/dx=2 du=2dx 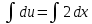 u=2x+с y’=2x+c1-еще одно ур. с раздл.перем. dy/dx=2x+c1 dy=(2x+c1)dx 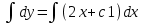 Y=x^2 +c1x+c2 Общее решение задает множество парабол. Для того, чтобы из множества парабол, проходящих через точку Р0, выбрать подходящую необ-мо выбрать направление, т.е. tg угла наклона касательной к этой точке. y’ 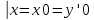 (2) (2)и (2) – начальные условия для нахождения частного решения ур. 2го порядка. Пусть в нашем ур. y 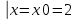 , y’ , y’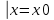 =-1 =-1Y=x^2+c1x+c2 2=0+c1*0+c2 Y’=2x+c1 → -1=2*0+c1 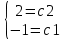 → y=x^2-x+2 → y=x^2-x+2Все сказанное в этом примере справедливо для всех ур. 2го порядка. Общее решение ДУ 2го порядка будем иметь вид: Y=ϕ(x, c1, c2) или ϕ(x, y, c1, c2) =0 Теорема Коши ( о существовании и единственности решения) Пусть функции f(x, y, y’) , f’y(x, y, y’), f’y’(x, y, y’) определены и непрерывны в некоторой области G изменения переменных x, y, y’. Тогда какова бы ни была точка (x0, y0, y’0)ϵG сущ-ет единственное решение ДУ удовлетворяющее данным нач. условиям: Y=ϕ(x, y, y’) y 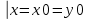 y’ 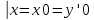 для того чтобы функция y=ϕ(x, c1, c2) была общим решением ДУ y’’=f(x, y, y’) необходимо: при любых значениях с1 и с2 y=ϕ(x, c1, c2) каковы бы ни были нач.условия y 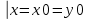 и y’ и y’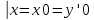 сущ-ют значения с10 и с20 такие, что после подстановки их вместо с1 и с2, мы получаем частное решение y=ϕ(x, c10, c20), удовлетворяющее данным нач.условиям. с10 и с20 находятся из системы 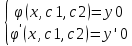 порядка и его решение. порядка и его решение. | Определение Линейного диф. Урав 2- го порядка. Его решение. ДУ вида a0(x)y’’+a1(x)y’+a2(x)y=b(x) (1) Где a0(x), a1(x), a2(x), b(x) – некоторые функции х , причем a0(x) 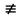 0, наз-ся линейным ДУ 2го порядка. Если b(x)=0, то ур. (1) примет вид : a0(x)y’’+a1(x)y’+a2(x)y=0(2), и будет наз-ся линейным однородным ДУ 2го порядка. 0, наз-ся линейным ДУ 2го порядка. Если b(x)=0, то ур. (1) примет вид : a0(x)y’’+a1(x)y’+a2(x)y=0(2), и будет наз-ся линейным однородным ДУ 2го порядка.Если b(x)=0, то ур. наз-ся линейным неоднородным ДУ 2го порядка. Для таких ур. справедливо все, что было сказано об ур-ниях 2-го порядка. В том числе и теорема о существовании и единственности решения ( теорема Коши) Теорема Коши. Пусть функции a0(x), a1(x), a2(x), b(x), коэффициенты при y’’, y’, y и правая часть в ур. (1) определены и непрерывны на некотором интервале (α, β). Тогда для любого х0ϵ(α, β) сущ-ет единственное решение y=ϕ(x), удовлетворяющие данным нач.условиям: y’ 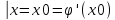 y 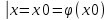 теорема 1. Пусть у1и у2 яв-ся частными решениями ЛОДУ2го порядка: a0(x)y’’+a1(x)y’+a2(x)y=0, тогда их линейная комбинация с1у1+с2у2 также яв-ся решением данного уравнения ( с2 и с1 любые const) докозательство: так как у1 и у2 –решения ур, то они обращают её в истинное уравнение. a0y1’’+a1y1’+a2y1=0 a0y2’’+a1y1’+a2y2=0 a0(c1y1+c2y2)’’+a1(c1y1+c2y2)’+a2(c1y1+c2y2)=0 возьмем производную и перегруппируем в одну скобку с слагаемым у1, в другую с у2; с1 и с2 вынесем за скобки: (c1a0y1’’+c1a1y1’+c1a2y1)+ (c2a0y2’’+c2a1y2’+c2a2y2)=c1*(a0y’’+a1y1’+a2y1)+ c2(a0y2’’+a1y2’+a2y2)=0 При подстановке в ур. выражение с1у1+с2у2 вместо у получим истинное равенство,оно яв-ся решением. Два частных решения у1 и у2 ЛОДУ 2го п. образуют фундаментальную систему решений на некотором интервале (α, β), если для всех х0ϵ(α, β) определитель W(x) = 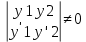 / этот определитель наз-ся определитель Вронского. / этот определитель наз-ся определитель Вронского. | 36. ЛОДУ 2го п. с пост. Коэф. Рассм. Ур. a0y’’+a1y’+a2y=0, а0, а1, а2-некоторые числа и а0 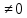 . .Будем искать частные решения этого ур. в виде у= 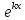 . Подставив в ур. вместо y, y’, y’’ функцию у= . Подставив в ур. вместо y, y’, y’’ функцию у=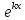 и её производные: и её производные:a0( 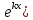 ’’+a1( ’’+a1(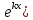 ’+a2( ’+a2(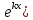 =0 =0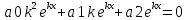 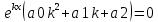 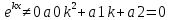 -квадратное ур., наз-ся характеристическим ур.-нием. При его решении возможны 3 случая -квадратное ур., наз-ся характеристическим ур.-нием. При его решении возможны 3 случаяПусть Д>0 Тогда харак. Ур. имеет 2 различных действительных корня: к1≠к2, к1,к2ϵR у1= 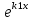 у2= у2=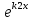 проверим образуют ли они фундаментальную систему решений: W(y1, y2)= 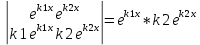 -k1 -k1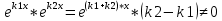 y=c1y1+c2y2 y=c1* 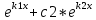 Д=0 Тогда харак. Ур. имеет 2 одинаковых корня: к1=к2 у1= 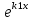 у2=х* у2=х*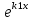 W(y1, y2)= 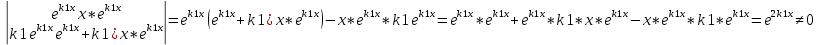 Y=c1* 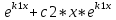 Y= 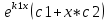 Д<0. Тогда харак.ур. имеет 2 комплексных корня. k1=α+iβ k2= α-iβ y1= 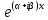 y2= y2=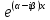 для обоих корней применим формулу эйлера: y1= 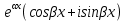 , y2= , y2=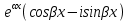 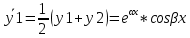 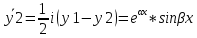 Нетрудно показать что 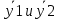 образуют фунд.сис.реш. образуют фунд.сис.реш.Тогда, y=c1* 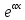 *cosβx+c2* *cosβx+c2*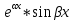 Y= 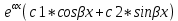 |
| 39. Метод вариации произвольной постоянной для ЛНДУ. Рассмотрим линейное неоднородное дифференциальное уравнение 2-го порядка: y”+py’+qy=f(x) Ищем решение в виде y=y*+ȳ,где y* - общее решение однородного уравнения, ȳ - частное решение неоднородного ур. Пусть y*=С1у1+С2у2, у1 и у2 частные решения однор. ур. составляющих сиситему.Заменим С1 и С2 на С1(х) и С2(х) и потребуем, чтобы ȳ=С1(х)у1+ С2(х)у2 являлись частным решением неоднор. ур. ȳ’= С1’(х)у1+ С1(х)у1'+ С2’(х)у2+ С2(х)у2’ Потребуем , что С1’(х)у1+ С2’(х)у2=0 (*) Тогда ȳ’= С1(х)у1’+ С2(х)у2’ ȳ” = С1’(х)у1’+ С1(х)у1“ + С2’(х)у2’+ С2(х)у2“ (С1’(х)у1’+ С1(х)у1“ + С2’(х)у2’+ С2(х)у2“)+p(С1(х)у1’+ С2(х)у2’)+q(С1(х)у1+ С2(х)у2)=f(x) С1(х)(у1”+py1’+qy1)+C2(x)(y2”+py2’+qy2)+C1’(x)y1’+C2’(x)y2’=f(x) C1(x)y1’+C2’(x)y2’=f(x) (**) Соотношения * и ** образуют систему 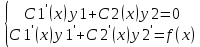 ∆= 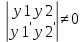 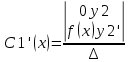 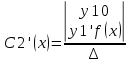 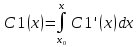 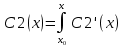 | 40. Системы диф. урав Часто на практике необх=мо найти несколько ф. зависящих от одной переменной и связываюзий несколькими ДУ 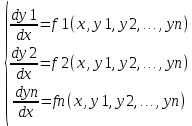 (*) (*)Для таких систем имеет место теорема о сущ-нии единственности решения. Решением системы будет совокупность функций yi=ϕi(x), i= 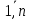 , подстановка кот-х в систему превращает каждое уравнение в истинное равенство. , подстановка кот-х в систему превращает каждое уравнение в истинное равенство.Теорема . Пусть ф. fi(x, y1, … , yn), i= 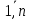 правые части ур. нормальной системы (*) и их частные производные правые части ур. нормальной системы (*) и их частные производные 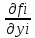 определены и непрерывны в некоторой области изменения переменной(x, y1, … , yn). Тогда какова бы ни была точка (x0, y10, … , y0n) сущ-ет единственное решение этой системы yi=ϕi(x), ), i= определены и непрерывны в некоторой области изменения переменной(x, y1, … , yn). Тогда какова бы ни была точка (x0, y10, … , y0n) сущ-ет единственное решение этой системы yi=ϕi(x), ), i=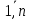 , удовлетворяющее данным нач.условиям yi , удовлетворяющее данным нач.условиям yi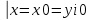 . . | Задачи, приводящие к понятие определенного двойного интеграла, понятия. Задача на вычисление объема. Рассм. Тело в пространстве, ограниченное сверху условной поверхностью z=f(x,y), снизу плоскостью ХОУ, а по бокам-цилиндрической поверхностью, образующие кот-ой параллельны оси ОZ. Эта поверхность вырезает на пл-ти ХОУ область Д. Поставим задачу найти объем этой области. Разобьем область Д , основание тела, на части с площадями ΔSi. В каждой из этих частей выберем произвольную точку Mi(xi, yi). В точках Mi восстановим перпендикуляр до пересечения с поверхностью z=f(x,y), кот-ое ограничивает наше тело сверху. Длины таких перпендикуляров равны f(xi,yi), i= 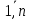 . нарисуем цилиндрическое тело с основанием ΔSi и высотой f(xi,yi), i= . нарисуем цилиндрическое тело с основанием ΔSi и высотой f(xi,yi), i=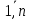 . Объем каждого из этих столбиков можно найти ΔVi= f(xi,yi)*ΔSi , а сумма объемов этих столбиков приблизительно равна объему тела: . Объем каждого из этих столбиков можно найти ΔVi= f(xi,yi)*ΔSi , а сумма объемов этих столбиков приблизительно равна объему тела:V 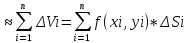 Чем больше n, тем точнее значение V= 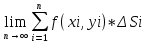 Задача о массе острой пластины Рассм.пластину, кот-ая представляет собой область Д, толщиной кот-го можно пренебречь. Пусть пластинка неоднородная с равномерно распределенной плотностью ƍ=f(x,y) .разобьем пластинку на n частей, в каждой из которых выберем произвольную точку Mi(xi,yi) и будем считать, что на данной участке плотность постоянна и равна значению в этой точке. Тогда массу отдельного кусочка можно сосчитать mi 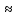 ƍf(xi,yi)*ΔSi ƍf(xi,yi)*ΔSiТогда массу всей пастинки можно сосчитать как сумму этих произведений: m 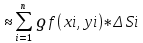 Чем больше n тем точнее значение, и за точное значение массы примем: m= 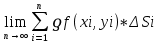 |
| Определение двойного интеграла. Пусть дана ф. определенная и непрерывная в каждой точке, ограниченная замкнутой плоскостью Д на пл-ти ХОУ. Разобьем область Д на части с площадями ΔSi В каждой из этих частей выберем точку Mi(xi,yi), i= 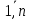 Составим сумму вида: 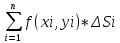 (1), кот-ую будем наз-ть двумерной интегральной суммой (1), кот-ую будем наз-ть двумерной интегральной суммойРассм. Предел суммы (1) 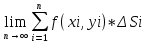 (2) (2)Если сущ-ет конечный предел (2) интегральной суммы (1) не зависящий ни от способа разбиения области Д на части, ни от выбора в них промежуточных точек Mi, то этот предел наз-ся двойным интегралом от функции f(x,y) по области Д и обозначается: 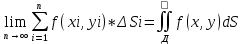 (3) (3)Здесь f(x,y)-подинтег.ф. Ds-элемент площади Д-область интегрирования Теорема о сущ-нии дв.интеграла. Для всякой ф. f(x,y) определенной и непрерывной в замкнутой ограниченной области Д, на пл-ти ХОУ площадью ΔSi сущ-ет двойной интеграл 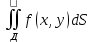 . .Разделение области Д на части проводится произвольно, поэтому удобно это сделать прямыми параллельными координатным осям. Тогда каждый из участков яв-ся прямоугольником со сторонами Δxi и Δyi и площадь находим просто: ΔSi=Δxi*Δyi dS=dxdy И тогда двойной интеграл примет вид: 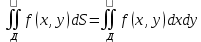 (4) (4) | Свойства двойного интеграла. Постоянный множитель выносится за знак дв.ин. 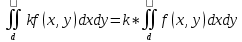 Дв. Интеграл от алгеб.суммы равен алгеб.сумме дв-х интегралов: 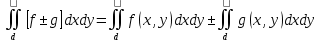 Если ф. f(x,y)⩾0 по области Д, то и дв.интеграл от этой ф. тоже 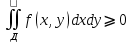 . .При чем если хотя бы в одной точке в этой области f(x,y)>0, тогда 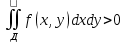 . .Если ф. f(x,y) и φ(x,y) Удовлетворяют неравенству f(x,y)⩾ φ(x,y) в области Д, то и дв.интегралы удовлетворяют такому же неравенству 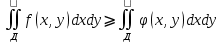 Если область Д можно представить или разбить на конечное число частей, то дв. Интеграл от ф. f(x,y) можно представить как сумму дв-х интегралов по каждой из этих областей. Д=Д1+Д2+Д3+…+Дn Теорема о среднем Если функция f(x,у) определена и непрерывна в замкнутой ограниченной области Д площадью ΔSi, то сущ-ет по крайней мере одна точка Р0(х0, у0) в области Д что имеет место равенство: 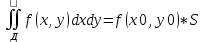 | |
