математика. математика практические. Решить уравнения, допускающие понижение порядка
 Скачать 40.09 Kb. Скачать 40.09 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ МАТЕМАТИКА Группа Студент МОСКВА 2019 Тема 14 Решить уравнения, допускающие понижение порядка: x2y”=y’2 В это уравнение второго порядка явно не входит неизвестная функция, следовательно полагая y’=z(x), y”=z’, получим дифференциальное уравнение первого порядка: x2z’=z” dz/z”= dz/x2 1/z= 1/x+ c y’=z=x/1+cx dy=1cx/ c1+cz dx = 1/c*(1+cx/1+cx)*dx- (1/1+cx)dx) y=x/c- ln(1+cx) / c2 + c^ 2)F(y, y’, y”, …, y^n)=0 p(y)=y’ y”=pp’, т.к. y”= dy’/ dx = dp/dy * dy/dx= p’p y’²+ 2yy”=0 Сделаем заменy y’=p Тогда y”=pp” Исходное уравнение примет вид p² + 2ypp’ = 0 p(p+2yp’)=0 1)p=0 =˃ y’=0 =˃ y=C 2) p+2yp’=0 2y*dp/dy= -p dp/p= -dy/2y ln |p|= - ½ ln|y| +C1 p= C1/ √y y’= C1/√y √ydy=C1dx 2/3 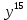 = C1x+C2 = C1x+C2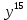 =1.5C1x+1.5C2= C3x+C4 =1.5C1x+1.5C2= C3x+C4 Возведем обе части в квадрат 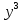 =(С1ч+С2)² =(С1ч+С2)²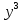 =(С1ч+С2)², y=C, C, C1, C2ϵ R =(С1ч+С2)², y=C, C, C1, C2ϵ Ryy”=y’²-y’³ y’=p(y) y”=p* dp/dy yp* dp/dy= p²-p³ Полученное уравнение распадается на два: p=0 и y* dp/dy= p-p² Из первого следует, что y=C И из второго p=y’= y/C1+y Интегрируя последнее уравнение, имеем x=C1 ln|y|+y+C2 y”²+y’=xy” y’=z y”=z’ z’²+z= xz’ z’=p dz=p dx p²+z=px x= (p²+z)/p dz=p[ (2p²-p²x)/p²dp+ 1/p dz ] dz= (2p²-z)/p dp+dz p²-z=0 z=p², x=2p²/p= 2p z=x²/4 y’=1/4x” dy=1/4x”dx y=x³/12 +C 2y’(y”+2)= xy”² y’=z 2z(z’+2)=xz’² z’=p 2z(p2)=xp² z= xp² / 2(p+2) dz=pdx= p²dx / 2(p+2)+ x(p²+4p)dp / 2(p+2) ² dx/x= dp/ (p+2); p≠0, p≠-2, p≠-4 x=C1(p+2) z=C1p²/2 z(x)= (x-C1)² / C1 3C1y=(x-C1)³+C2 y=C, y=c-2x² yy”+y=y’² y’=p(y), y”=p’p =˃ upp’+y=p² p= 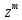 =˃ m=1/2, p=√z =˃ z’+2=2 z/y, y≠0 =˃ m=1/2, p=√z =˃ z’+2=2 z/y, y≠0z=ty, z’=t’y+t =˃ t’y=t-2 t’/ (t-2) = 1/y t=C1y+2 p=y’=√y(C1y+2) x+C1= ∫ dy/ √C1y²+2y y’”y’²=y”³ y’=t, y”=t’, y’”=t” t’=p, t”=pp’ pp’t²=p³ p=0 =˃ t’=0 =˃ t=C=˃ y’=c=˃y=Cx+C1 p’t²=p² dp/p²= dt/t² -1/p—1/t-C 1/p=1/t +C= Ct+1 / t p=t/ Ct+1 t’= t / Ct+z dt/dx=t/ Ct+1 dt(C+ 1/t)=dx x=Ct+ln|t+C1 Найдем полный дифференциал от обеих частей dx= Cdt+1/t dt Учитывая dy/dx=t =˃dx= dy/t dy/t=Cdt+1/t dt dy=Ctdt+dt=dt(Ct+1) y=∫ (Ct+1)dt=Ct²/c +t + C2 x=Ct+ln|t|+C1 y=Ct²/2 + t + C2 Решить линейные однородные уравнения с постоянными коэффициентами y”+y’-2y=0 λ²+λ-2=0 λ1=1 λ2=-2 y=C1  +C2 +C2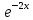 2y”-5y’+2y=0 2λ²-5λ+2=0 D=25-16=9 λ1,2= (5±√9) / 4= (5±3)/4= 1/2';2 y=C1 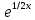 C2 C2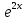 y”-4y’+5y=0 λ²-4λ+5=0 λ1,2=2±√4-5= 2±i y=C1 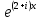 +C2 +C2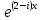 =C1 =C1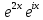 +C2 +C2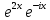 = = C1 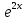 (cosx+I sinx)+ C2 (cosx+I sinx)+ C2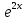 (cosx-isinx)= (cosx-isinx)= 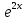 (C1cosx+C2sinx) (C1cosx+C2sinx) y”’-8y=0 λ³-8=0 λ1=2, λ2=-1+i√3, λ2=-1-i√3 y=C1 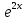 +(C2 +(C2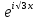 +C3 +C3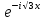 ) ) Воспользовавшись формулами Эйлера cosφ=1/2( 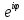 + +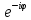 ), sinφ=1/2i( ), sinφ=1/2i(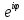 - -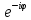 ) )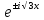 = cos√3x±i sin√3x = cos√3x±i sin√3xy=C1 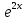 +((C2+C3)cos√3x+i(C2-C3)sin√3x) +((C2+C3)cos√3x+i(C2-C3)sin√3x) C2= 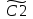 +i +i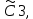 C3= C3=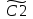 -i -i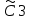 , где , где 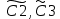 - действительные произвольные потоянные - действительные произвольные потоянныеy=C1 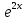 + + ( (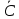 2 cos√3x+ 2 cos√3x+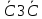 sin√3x) sin√3x)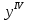 -y=0 -y=0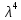 -1=0 -1=0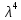 =1 =1λ1,2=±1 λ3,4=±i y=C1  +C2 +C2 +C3sinx+C4cosx +C3sinx+C4cosxy=C1cos2x+C2sin2x 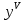 -10y”’+9y’=0 -10y”’+9y’=0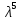 -10 -10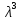 +9λ=0 +9λ=0λ( 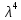 -10 -10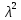 +9)-0 +9)-0λ( 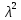 -1)( -1)(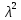 -9)=0 -9)=0λ1=0 λ2,3=±1 λ3,4=±3 y(x)=C1+C2  +C3 +C3 +C4 +C4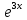 +C5 +C5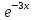 y”’-3y”+3y’-y=0 (λ-1)³=0 λ1,2,3=1 y=  (C1+C2x+C3 (C1+C2x+C3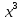 ) )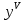 +8y”+16y’=0 +8y”+16y’=0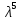 +8 +8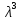 +16λ=0 +16λ=0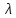 ( (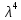 +8 +8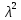 +16)=0 +16)=0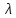 ( (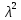 +4)²=0 +4)²=0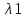 =0; λ2= λ3=2i; λ4= λ5=-2i =0; λ2= λ3=2i; λ4= λ5=-2i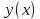 =C1+(C2+C3x)cos2x+(C4+C5x)sin2x =C1+(C2+C3x)cos2x+(C4+C5x)sin2xРешить линейные неоднородные уравнения с постоянными коэффициентами y”-2y’-3y= 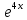 Возьмем уравнение y”-2y’-3y=0 =˃ 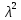 -2λ=0 =˃ λ1=-1, λ2=3 =˃ -2λ=0 =˃ λ1=-1, λ2=3 =˃y=C1  +C2 +C2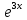 f(x)= 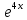 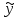 =Q0(x) =Q0(x)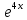 =a0 =a0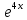 5a0 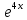 = =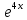 a0=1/3, 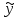 =1/3 =1/3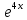 y=C1  +C2 +C2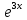 +1/5 +1/5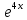 C1+C2+1/5=1, -C1+3C2+4/5=0 y=4/5  +1/5 +1/5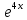 y”-y=2  -x² -x²y=C1  +C2 +C2 y”-y=2  , y”-y=-x² , y”-y=-x²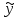 1=a0x 1=a0x , , 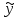 2=b0x²+b1x+b2 2=b0x²+b1x+b22a0  ≡2 ≡2 , 2b0-b0x²-b1x-b2≡-x² , 2b0-b0x²-b1x-b2≡-x²a0=2, b0=1, -b1=0, 2b0-b2=0 или b2=2 y= 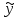 1+ 1+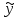 2=x 2=x +x²+2 +x²+2y=C1  +C2 +C2 +x +x +x²+2 +x²+2y”-3y’+2y=sinx y=C1  +C2 +C2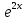 sinx=1/2i* 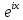 -1/2i* -1/2i*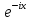 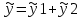 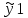 =a0 =a0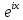 , , 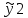 =b0 =b0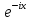 =˃ =˃ 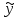 = a0 = a0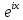 + b0 + b0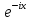 a0=3/20 – i/20, b0= 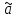 0=3/20 + i/20 0=3/20 + i/20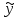 = a0 = a0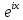 + +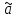 0 0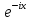 =(a0+ =(a0+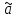 0)cosx+i(a0+ 0)cosx+i(a0+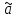 0)sinx= 3/10cosx+1/10sinx 0)sinx= 3/10cosx+1/10sinxy=C1  +C2 +C2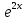 +3/10cosx+1/10sinx +3/10cosx+1/10sinxy”+2y’-3y=x²  λ²+2λ-3=0 λ1=-3, λ2=1 y=C1 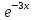 +C2 +C2 y=x(ax²+bx+c)  =(ax³+bx²+cx) =(ax³+bx²+cx) y’=(3ax²+2bx+c)  + (ax³+bx²+cx) + (ax³+bx²+cx) =(ax³+(3a+b)x²+(2b+c)x+c) =(ax³+(3a+b)x²+(2b+c)x+c) y”=(3ax²+(6a+2b)x+2b+c+ax³+(3a+b)x²+(2b+c)x+c)  = =(ax³+(6a+b)x²+(6a+4b+c)x+2b+2c)  ax³+(6a+b)x²+(6a+4b+c)x+2b+2c+2ax³+(6a+2b)x²+(4b+2c)x+2c-3ax³-3bx²-3cx=x²  12ax²+(6a+8b)x+2b+4c=x² 12a=1 6a+8b=0 2b+4c=0 a=1/12, b=-3/4a=-1/16, c=-1/2b=1/32 y=(x³/12-x²/16+x/32)  y=C1 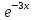 +C2 +C2 +=(x³/12-x²/16+x/32) +=(x³/12-x²/16+x/32) y”+y=xsinx y=C1sinx+C2sinx y2=x((Ax+B)sinx+(Cx+D)cosx)= Ax²sinx+Bxsinx+Cx²cosx+Dxcosx y’=2Axsins+Ax²cosx+Bsinx+Bxcosx+2Cxcosx-Cx²sinx+Dcosx-Dxsinx y”=2Asinx+2Axcosx+2Axcosx-Ax²sinx+Bcosx+Bcosx-Bxsinx+2Ccosx-2Cxsinx- -2Cxsinx-Cx²cosx-Dsinx-Dsinx+Dxcosx=xsinx A-D=0, B+C=0, 4A=0, -4C=1, D=0, B=1/4, A=0, C=-1/4 =˃ y=C1cosx+C2sinx+x/4sinx-x²/4cosx Решить уравнения методом вариации произвольных постоянных y”+3y’+2y=1/ 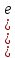 ) )λ²+3λ+2=0 λ1=-1, λ2=-2 y=C1  +C2 +C2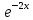 C1  +C2 +C2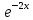 =0 =0-C1  -C2 -C2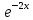 =1/( =1/(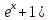 -C2 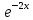 =1/( =1/(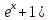 C2=- 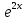 /( /(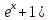 C2=-∫ 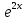 /( /(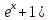 dx= -∫ dx= -∫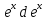 /( /(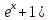 =-∫(1- 1/( =-∫(1- 1/(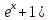 )d )d =- =- +ln( +ln(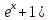 +C3 +C3C1  -1/( -1/(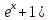 =0 =0C1=  /( /(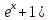 C1=∫ 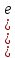 /( /(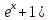 ) dx= ∫ ) dx= ∫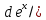 ( (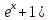 =ln( =ln(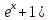 +C4 +C4y=ln( 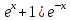 - - +ln( +ln(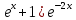 +C4 +C4 +C3 +C3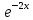 = =( 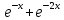 )ln( )ln( +1)+(C4-1) +1)+(C4-1) +C3 +C3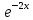 = =(  + +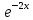 )ln( )ln( +1)+C1 +1)+C1 +C2 +C2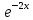 y”+y=1/sinx y”+y=0 φ(λ)=λ²+1 λ1=i, λ2=-i y1=cosx, y2=sinx y0=C1cosx+C2sinx C1cosx+C2sinx=0 -C1sinx+C2cosx=1/sinx C1cos²x+C2sinxcosx=0 -C1sin²x+C2sinxcosx=1 C1(cos²x+sin²x)=-1 C1=-1, C2=ctgx C1(x)=-x+C1 C2(x)=ln|sinx|+C2 y=(C1-x)cosx+(C2+ln|sin|)sinx=C1cosx-xcosx+C2sinx+ln|sinx|-sinx= C1cosx+C2sinx+sinx ln|sinx|-xcosx x³(y”-y)=x²-2 y=C1  +C2 +C2 y=C1(x)  +C2(x) +C2(x) C1(x)  +C2(x) +C2(x) =0, C1(x) =0, C1(x) +C2(x) +C2(x) =1/x – 2/x³ =1/x – 2/x³C1(x)=1/2(-2/x³ + 1/x)  , C2(x)=1/2(-1/x + 2/x³) , C2(x)=1/2(-1/x + 2/x³) C1(x)=1/2∫(-2/x³+1/x)  dx +C1, C2(x)=1/2∫(-1/x+ 2/x³) dx +C1, C2(x)=1/2∫(-1/x+ 2/x³) dx+C2 dx+C2C1(x)=1/2  (-1/x+ 1/x²)+C1, C2(x)= 1/2 (-1/x+ 1/x²)+C1, C2(x)= 1/2 (-1/x- 1/x²)+C2 (-1/x- 1/x²)+C2y=C1  +C2 +C2 - 1/x - 1/xРешить линейные уравнения с переменными коэффициентами x²y”-xy’-3y=0 λ(λ-1)- λ-3=0 λ²-2 λ-3=0 λ1=-1, λ2=3 y= C1  +C2 +C2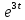 y=C1 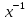 + C2x³ + C2x³x²y”’=2y’ x²y”’-2xy’=0 x= 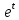 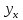 ’= ’=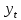 / /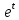 ; ; 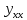 ”= ”=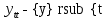 / /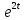 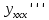 = =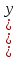 -3 -3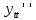 +2 +2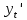 )/ )/ 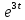 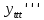 -3 -3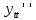 +2 +2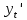 -2 -2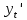 =0 =0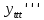 -3 -3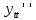 =0 =0λ³-3 λ²=0 λ=0, λ=3 y=(C1+C2)+C3 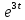 y=C1+C3x³+C2lnx x²y”-3xy’+5y=3x² (x-2)²y”-3(x-2)y’+4y=x λ(λ-1)-3λ+4=0 λ²-4λ+4=0 (λ-2)²=0 y=(C1+C2t) 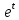 x-2= 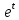 y”-4y’+4y= 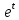 +2 +2y1=C1 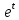 y1= 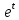 C1 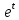 -4 -4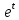 C1+4С1 C1+4С1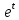 = =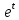 С1-4С1+4С1=1 y2=1/2 y=1/2+ 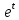 +(C1+C2t) +(C1+C2t)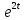 =1/2+x-2+(C1+C2ln|x-2|)(x-2)² =1/2+x-2+(C1+C2ln|x-2|)(x-2)²x³y”-2xy=6lnx x²y”-2y=6lnx/x x= 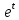 y=y(t) y’= 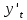 / / 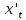 = = 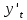 / /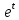 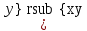 =( =(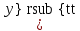 - -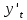 )/ )/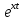 =˃ =˃ 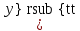 - -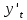 -2y=6t/ -2y=6t/ λ²-λ-2=0 λ1=-1 λ2=2 y=C1  +C2 +C2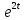 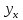 =(at+b)t =(at+b)t =at² =at² +bt +bt ) )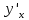 =2at =2at -at² -at² +b +b -bt -bt 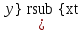 =2a =2a -2at -2at -2at -2at +at² +at² -b -b -b -b +bt +bt 2a  -4at -4at +at² +at² -2b -2b +bt +bt -2at -2at +at² +at² -b -b +bt +bt -2at² -2at² -2bt -2bt =6 =6 t t2a  -6at -6at -3b -3b =6 =6 t t2a-6at-3b=6t 2a-3b=0 -6a=6 a=-1, b=2/3 y=C1  +C2 +C2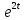 +(-t+ 2/3)t +(-t+ 2/3)t y=C1 1/X+ C2 x²+(-lnx + 2/3) lnx 1/x= C2x²+ 1/x(C1- 2/3lnx- ln²) x²y”-xy’+y=8x³ x= 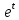 λ(λ-1)-λ+1=0 λ²-2λ+1=0 λ=1(2) y=(C1+C2t) 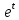 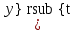 -2 -2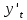 +y=8 +y=8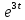 x=a 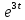 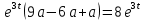 4a=8 a=2 y=2 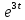 y=(C1+C2t) 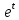 +2 +2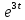 t=ln|x| y=(C1+C2ln|x|)x+2x³ |
