Конспект по теме электрические цепи постоянного и синусоидального тока. Конспект к видеоуроку Электрические цепи постоянного и синусоида. Электрические цепи постоянного и синусоидального тока
 Скачать 49.88 Kb. Скачать 49.88 Kb.
|
|
Конспект к видео-уроку выполнил И. Шарафутдинов Электротехника и электроника. Тема: Электрические цепи постоянного и синусоидального тока Расчеты цепи постоянного тока Общий анализ сложной электрической цепи, когда известны конфигурация цепи и параметры ее элементов, состоит в нахождении токов и напряжений во всех ветвях, а также мощности на участках цепи. Эта задача может быть решена с помощью уравнений электрического состояния. При выборе контуров для составления уравнений следует исходить из того же принципа независимости уравнений. Контуры необходимо выбирать так, чтобы в систему составляемых уравнений вошли все ветви схемы, а в каждый из контуров — наименьшее число ветвей. Упростить расчет сложных электрических цепей можно несколькими методами: 1. Метод наложения состоит в предварительных преобразованиях, позволяющих сложную цепь представить несколькими простыми цепями. Его суть заключается в том, что токи в ветвях определяются как алгебраическая сумма их составляющих от каждого источника. То есть каждый источник тока вносит свою часть в каждый ток в цепи, а чтобы найти эти токи, нужно найти и сложить все составляющие. Таким образом, мы сводим решение одной сложной цепи к нескольким простым (с одним источником). Порядок расчета: 1 – Составление частных схем, с одним источником ЭДС, остальные источники исключаются, от них остаются только их внутренние сопротивления. 2 – Определение частичных токов в частных схемах, обычно это несложно, так как цепь получается простой. 3 – Алгебраическое суммирование всех частичных токов, для нахождения токов в исходной цепи. 2. Метод вспомогательных неизвестных (контурных токов или узловых потенциалов) заключается во введении неизвестных в расчеты, число которых существенно меньше числа ветвей цепи. 2. В методе контурных токов за неизвестные величины принимаются расчетные (контурные точки), которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи. Расчет токов ветвей по методу контурных токов выполняют в следующем порядке: 1- Вычерчиваем принципиальную схему цепи и обозначаем все элементы. 2 - Определяем все независимые контуры. 3 - Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). 4 - По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности. 5 - Решаем любым методом полученную систему относительно контурных токов и определяем их. 6 - Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.). 7 - Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви. 3. Метод узлового напряжения. Если разветвленная цепь имеет только два узла, или путем преобразования может быть приведена к двум узлам, то анализ таких цепей ведется методом двух узлов, который называется методом узлового напряжения. Он основан на применении первого закона Кирхгофа. Для расчета токов методом узловых потенциалов применяют обобщенный закон Ома. Алгоритмы упрощающие расчеты сложных цепейВ электротехнике часто приходится иметь дело с соединениями звездой или треугольником. В некоторых случаях расчет сложной цепи значительно упрощается, если треугольник сопротивлений заменить звездой сопротивлений, т. е. тремя ветвями, имеющими дополнительный общий узел ноль (рис. 1). В других случаях расчета цепей встречается необходимость звезду заменить треугольником. Эти взаимные замены треугольника и звезды сопротивлений должны быть эквивалентными, т. е. при соответственно равных напряжениях между вершинами А, Б и В треугольника и звезды токи IA, IБ, 1В в подводящих проводах, соединяющих эти вершины с остальной частью цепи, должны остаться без изменений. Равенство токов должно выполняться при любых изменениях и переключениях в остальной части цепи и, в частности, при обрывах некоторых ее ветвей.  Рис. 1. Соединение резисторов треугольником (а) и звездой (б) Сопротивления эквивалентной звезды rа, rб, rв находятся в определенных соотношениях с сопротивлениями треугольника rаб, rбв, rва. Для выяснения этой зависимости допустим сначала, что в вершине А произошел обрыв подводящего провода и, следовательно, ток Iа=0. Сопротивления между двумя оставшимися присоединенными вершинами Б и В для обеих схем должны быть одинаковы, чтобы были соответственно равны токи IБ и Iв в обеих схемах. После обрыва в вершине А сопротивления rб и rвв звезде соединены последовательно, а в треугольнике сопротивления rВА и rАБ соединенные последовательно, образуют одну ветвь с суммарным сопротивлением rВА + rАБ, параллельно которой подключено сопротивление rБв. Поэтому можно написать:  для случая обрыва в вершине Б, при котором ток IБ = 0, а затем провода В, при котором ток Iв=0, получим аналогичные выражения: 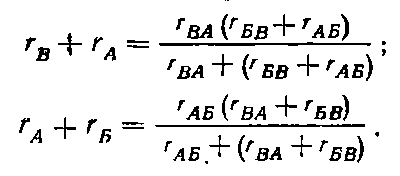 Чтобы преобразовать треугольник в звезду при заданных сопротивлениях сторон треугольника rаб, rбв, rва, требуется определить сопротивления лучей эквивалентной звезды rа, rб, rв . Для этого составим полусумму левых и правых частей уравнений:  В результате получим:   Таким образом, сопротивление луча эквивалентной звезды равно произведению сопротивлений двух сторон треугольника, которые присоединены к той же вершине, что и луч звезды, деленному на сумму сопротивлений, всех сторон треугольника. Если сопротивления треугольника равны друг другу: rаб = rбв=rва=rΔ, то будут равны друг другу и сопротивления звезды, т. е. rа = rб=rв=r λ, причем из формул получается простое соотношение: При обратном преобразовании звезды в эквивалентный треугольник, т. е. при заданных сопротивлениях rа,rб, rв, надо решить три уравнения относительно сопротивлений rаб, rбв: 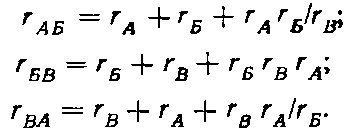 Таким образом, сопротивление стороны эквивалентного треугольника равно сумме сопротивлений двух лучей звезды, присоединенных к тем же вершинам, что и сторона треугольника, и их произведения, деленного на сопротивление третьего луча звезды. Необходимо при расчете цепей также помнить и о том, что в этих цепях происходит потеря напряжения в проводах. Участок электрической цепи, состоящий из двух проводов, которые соединяют источник питания с приемником, следует считать длинной линией, если сопротивление проводов нельзя пренебречь. Сопротивление обоих проводов определяется по формуле: 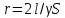 , ,где l – длина провода,  - площадь поперечного сечения. - площадь поперечного сечения.Мощность потерь в линии: 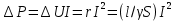 КПД линии :  , где , где 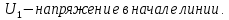 Цепи синусоидального тока. Методы расчетаВ принципе переменным током можно назвать всякий ток, который с течением времени изменяет свою величину, но в технике переменным током называют такой ток, периодически изменяет и величины и направление. Причем среднее значение силы такого тока за период Т равно нулю. Периодическим переменный ток называется потому, что через промежутки времени Т, характеризующие его физические величины принимают одинаковые значения. В электротехнике наибольшее распространение получил синусоидальный переменный ток, т.е. ток, величина которого изменяется по закону синуса (или косинуса), обладающий рядом достоинств по сравнению с другими периодическими токами. Переменный ток промышленной частоты получают на электростанциях с помощью генераторов переменного тока (трехфазных синхронных генераторов). Пусть в однородном магнитном поле постоянного магнита равномерно вращается с угловой скоростью 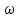 рамка площадью S. Магнитный поток через рамку Ф будет равен: Ф=BS cos рамка площадью S. Магнитный поток через рамку Ф будет равен: Ф=BS cos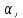 где где  - угол между нормалью к рамке n и вектором магнитной индукции B. Поскольку при равномерном вращении рамки n= B/t, то угол - угол между нормалью к рамке n и вектором магнитной индукции B. Поскольку при равномерном вращении рамки n= B/t, то угол  будет изменяться по закону будет изменяться по закону  = = 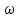 t и формула примет вид: Ф=BScos t и формула примет вид: Ф=BScos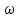 t. t. Поскольку при вращении рамки пересекающий ее магнитный поток все время меняется, то по закону электромагнитной индукции в ней будет наводиться ЭДС индукции Е: Е= -dФ/dt =BS 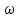 sin sin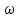 t = t =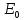 sin sin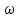 t.. Таким образом, в рамке возникнет синусоидальная ЭДС, а если замкнуть рамку на нагрузку, то в цепи потечет синусоидальный ток. t.. Таким образом, в рамке возникнет синусоидальная ЭДС, а если замкнуть рамку на нагрузку, то в цепи потечет синусоидальный ток.Круговая частота :  . .Частота колебаний: 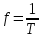 , где Т – период. , где Т – период.Фаза колебания:  . .Действующим значением тока называют соответствующий параметр такого состояния тока, при котором в данном проводнике за данный промежуток времени выделяется столько же теплоты, что и при переменном токе.  ; ; 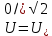 ; ;  В ходе этой лекции мы рассмотрели электрические цепи постоянного и синусоидального тока. Алгоритмы и методов расчета сложных цепей, а также цепи синусоидального тока и некоторые методы их расчета. |
