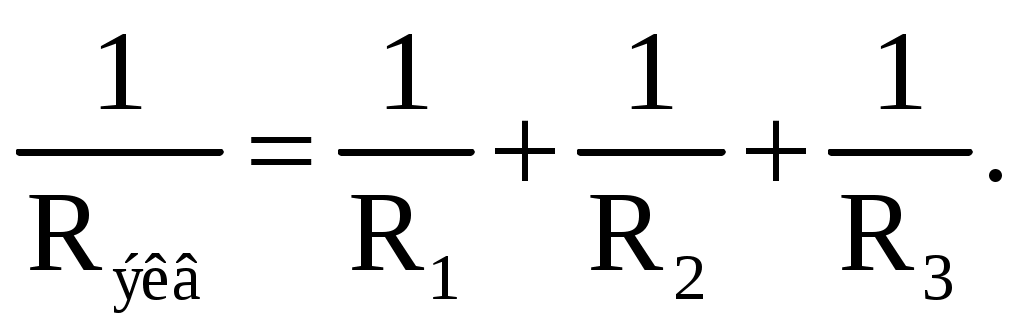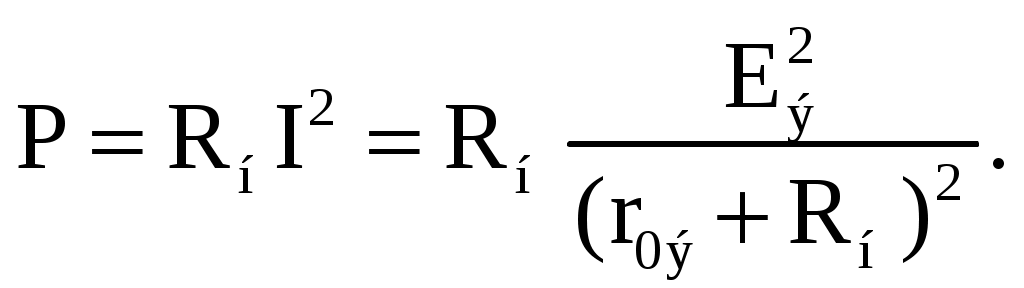ПОСТ ЛЕКЦИИ(1). Электрические цепи постоянного тока и методы их расчета электрическая цепь и ее элементы

• Название: Электрические цепи постоянного тока и методы их расчета электрическая цепь и ее элементы
• Дата: 03.10.2021
• Размер: 0.52 Mb.
• Имя файла: ПОСТ ЛЕКЦИИ(1).doc
• Тип: Задача; #240736
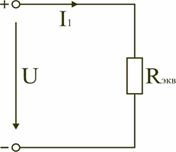
• страница: 1 из 2

ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА И МЕТОДЫ ИХ РАСЧЕТА

1. Электрическая цепь и ее элементы

В электротехнике рассматривается устройство и принцип действия основных электротехнических устройств, используемых в быту и промышленности. Чтобы электротехническое устройство работало, должна быть создана электрическая цепь, задача которой передать электрическую энергию этому устройству и обеспечить ему требуемый режим работы.

Электрической цепью называется совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электрическом токе, ЭДС (электродвижущая сила) и электрическом напряжении.

Для анализа и расчета электрическая цепь графически представляется в виде электрической схемы, содержащей условные обозначения ее элементов и способы их соединения. Электрическая схема реальной электрической цепи, обеспечивающей работу осветительной аппаратуры, представлена на рис. 2.1.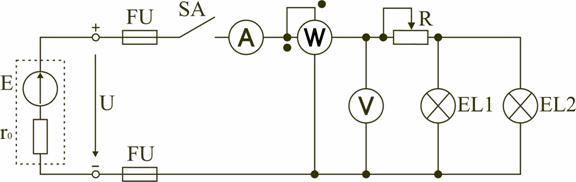


Рис. 2.1. Электрическая схема реальной электрической цепи
Все устройства и объекты, входящие в состав электрической цепи, могут быть разделены на три группы.

1. Источники электрической энергии (питания).

Общим свойством всех источников питания является преобразование какого-либо вида энергии в электрическую. Источники, в которых происходит преобразование неэлектрической энергии в электрическую, называются первичными источниками. Вторичные источники – это такие источники, у которых и на входе, и на выходе – электрическая энергия (например, выпрямительные устройства).

2. Потребители электрической энергии. Общим свойством всех потребителей является преобразование электроэнергии в другие виды энергии (например, нагревательный прибор).

Иногда потребители называют нагрузкой.

3. Вспомогательные элементы цепи: соединительные провода, коммутационная аппаратура, аппаратура защиты, измерительные приборы и т.д., без которых реальная цепь не работает.

Все элементы цепи охвачены одним электромагнитным процессом.

В электрической схеме на рис. 2.1 электрическая энергия от источника ЭДС E, обладающего внутренним сопротивлением r₀, с помощью вспомогательных элементов цепи передаются через регулировочный реостат R к потребителям (нагрузке): электрическим лампочкам EL₁ и EL₂.

2. Основные понятия и определения для электрической цепи

Для расчета и анализа реальная электрическая цепь представляется графически в виде расчетной электрической схемы (схемы замещения). В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают. Источник питания показывается как источник ЭДС E с внутренним сопротивлением r₀, реальные потребители электрической энергии постоянного тока заменяются их электрическими параметрами: активными сопротивлениями R₁, R₂, …, R_n. С помощью сопротивления R учитывают способность реального элемента цепи необратимо преобразовывать электроэнергию в другие виды, например, тепловую или лучистую.

При этих условиях схема на рис. 2.1 может быть представлена в виде расчетной электрической схемы (рис. 2.2), в которой есть источник питания с ЭДС E и внутренним сопротивлением r₀, а потребители электрической энергии: регулировочный реостат R, электрические лампочки EL₁ и EL₂ заменены активными сопротивлениями R, R₁ и R₂.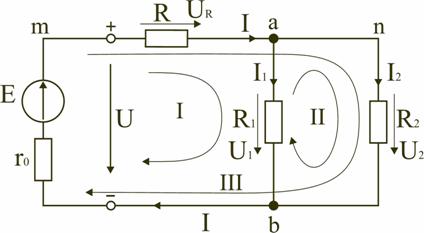


Рис. 2.2. Расчетная электрическая схема
Источник ЭДС на электрической схеме (рис. 2.2) может быть заменен источником напряжения U, причем условное положительное направление напряжения U источника задается противоположным направлению ЭДС.

При расчете в схеме электрической цепи выделяют несколько основных элементов.

Ветвь электрической цепи (схемы) – участок цепи с одним и тем же током. Ветвь может состоять из одного или нескольких последовательно соединенных элементов. Схема на рис. 2.2 имеет три ветви: ветвь bma, в которую включены элементы r₀, E, R и в которой возникает ток I; ветвь ab с элементом R₁ и током I₁; ветвь anb с элементом R₂ и током I₂.

Узел электрической цепи (схемы) – место соединения трех и более ветвей. В схеме на рис. 2.2 – два узла a и b. Ветви, присоединенные к одной паре узлов, называют параллельными. Сопротивления R₁ и R₂ (рис. 2.2) находятся в параллельных ветвях.

Контур – любой замкнутый путь, проходящий по нескольким ветвям. В схеме на рис. 2.2 можно выделить три контура: I – bmab; II – anba; III – manbm, на схеме стрелкой показывают направление обхода контура.

Условные положительные направления ЭДС источников питания, токов во всех ветвях, напряжений между узлами и на зажимах элементов цепи необходимо задать для правильной записи уравнений, описывающих процессы в электрической цепи или ее элементах. На схеме (рис. 2.2) стрелками укажем положительные направления ЭДС, напряжений и токов:

а) для ЭДС источников – произвольно, но при этом следует учитывать, что полюс (зажим источника), к которому направлена стрелка, имеет более высокий потенциал по отношению к другому полюсу;

б) для токов в ветвях, содержащих источники ЭДС – совпадающими с направлением ЭДС; во всех других ветвях произвольно;

в) для напряжений – совпадающими с направлением тока в ветви или элемента цепи.

Все электрические цепи делятся на линейные и нелинейные.

Элемент электрической цепи, параметры которого (сопротивление и др.) не зависят от тока в нем, называют линейным, например электропечь.

Нелинейный элемент, например лампа накаливания, имеет сопротивление, величина которого увеличивается при повышении напряжения, а следовательно и тока, подводимого к лампочке.

Следовательно, в линейной электрической цепи все элементы – линейные, а нелинейной называют электрическую цепь, содержащую хотя бы один нелинейный элемент.

3. Основные законы цепей постоянного тока

Расчет и анализ электрических цепей производится с использованием закона Ома, первого и второго законов Кирхгофа. На основе этих законов устанавливается взаимосвязь между значениями токов, напряжений, ЭДС всей электрической цепи и отдельных ее участков и параметрами элементов, входящих в состав этой цепи.

Закон Ома для участка цепи. Соотношение между током I, напряжением U_R и сопротивлением R участка аb электрической цепи (рис. 2.3) выражается законом Ома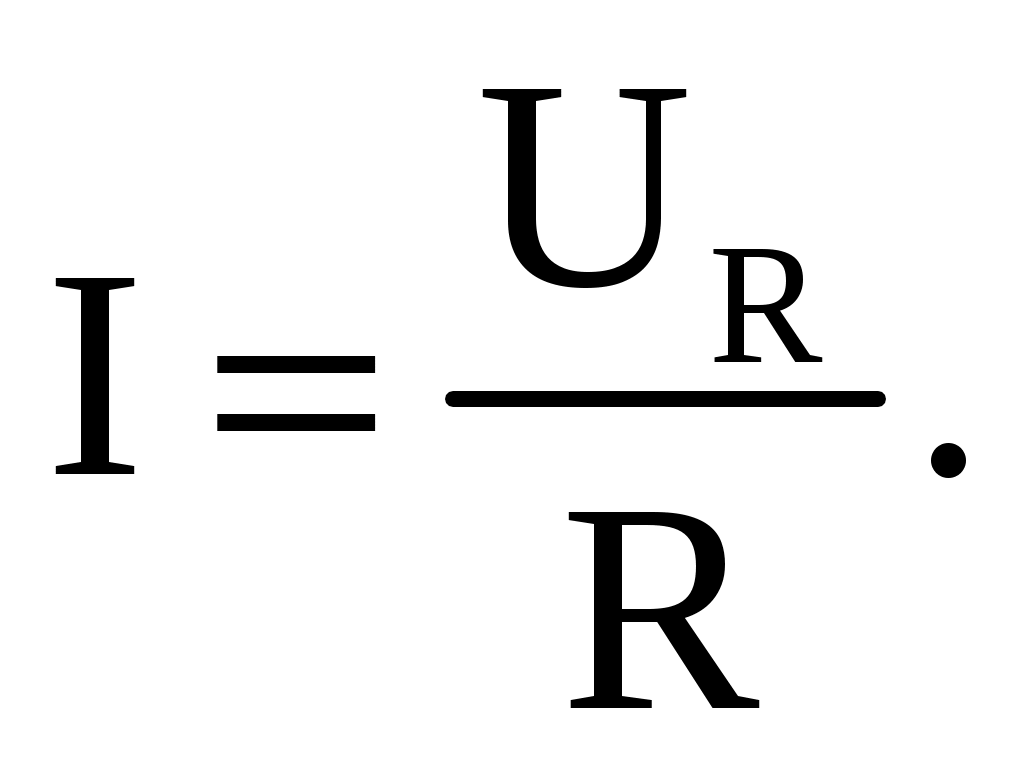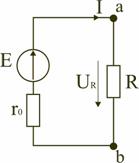




Рис. 2.3. Электрическая схема
В этом случае U_R = RI – называют напряжением или падением напряжения на резисторе R, а I – током в резисторе R.

При расчете электрических цепей иногда удобнее пользоваться не сопротивлением R, а величиной обратной сопротивлению, т.е. электрической проводимостью: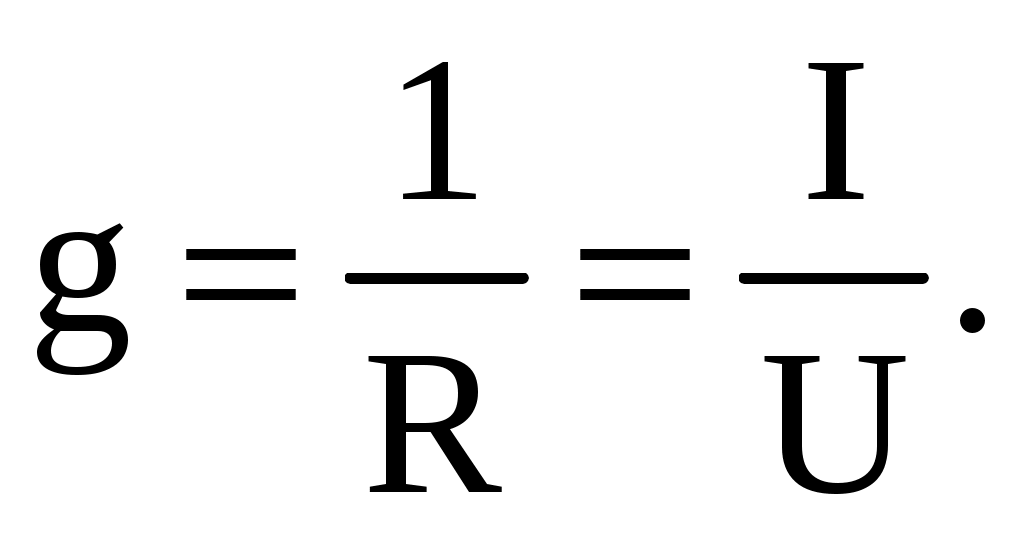



В этом случае закон Ома для участка цепи запишется в виде:

I = gU.

Закон Ома для всей цепи. Этот закон определяет зависимость между ЭДС Е источника питания с внутренним сопротивлением r₀ (рис. 2.3), током I электрической цепи и общим эквивалентным сопротивлением R_Э = r₀ + R всей цепи: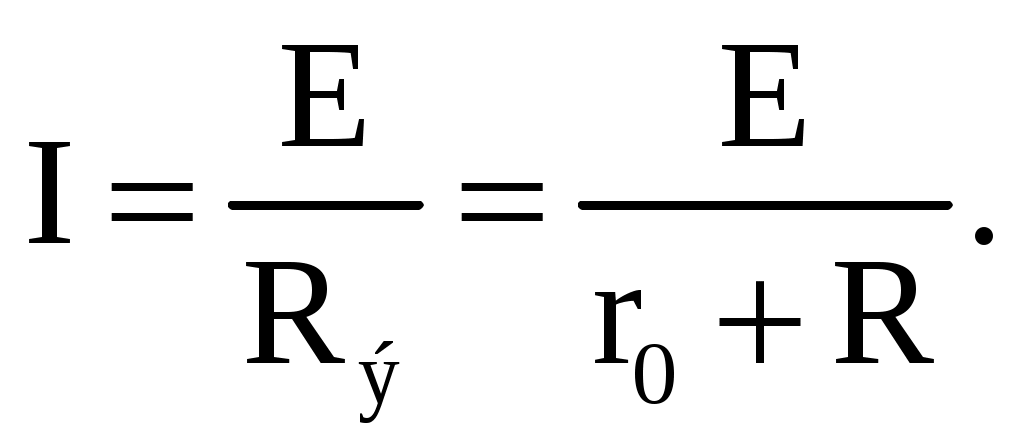



Сложная электрическая цепь содержит, как правило, несколько ветвей, в которые могут быть включены свои источники питания и режим ее работы не может быть описан только законом Ома. Но это можно выполнить на основании первого и второго законов Кирхгофа, являющихся следствием закона сохранения энергии.

Первый закон Кирхгофа. В любом узле электрической цепи алгебраическая сумма токов равна нулю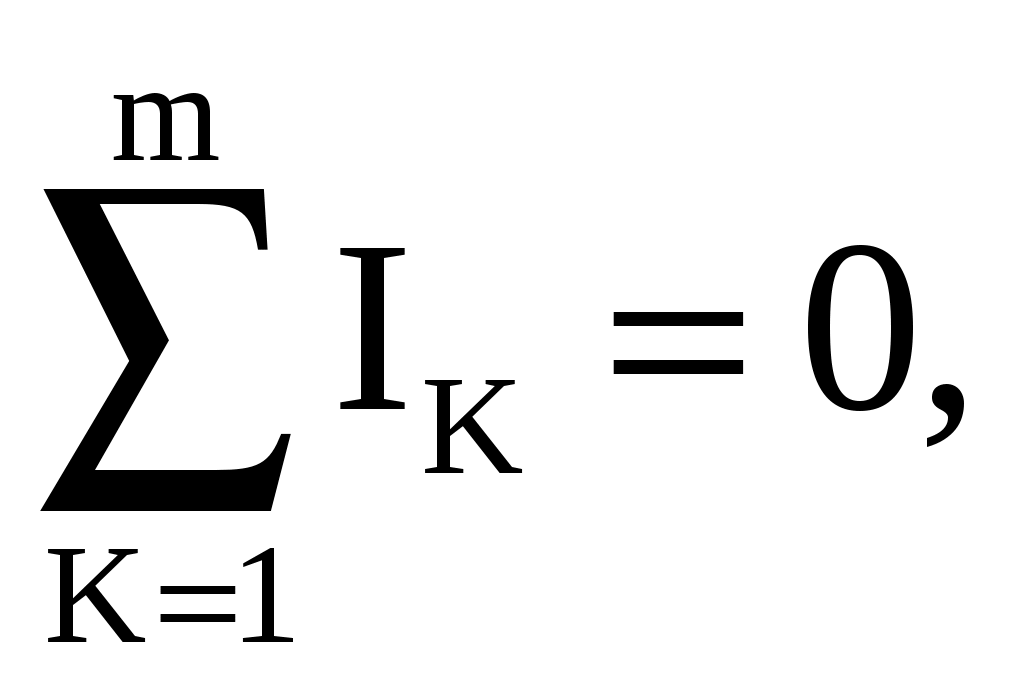



где m – число ветвей подключенных к узлу.

При записи уравнений по первому закону Кирхгофа токи, направленные к узлу, берут со знаком «плюс», а токи, направленные от узла – со знаком «минус». Например, для узла а (см. рис. 2.2)

I − I₁ − I₂ = 0.

Второй закон Кирхгофа. В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках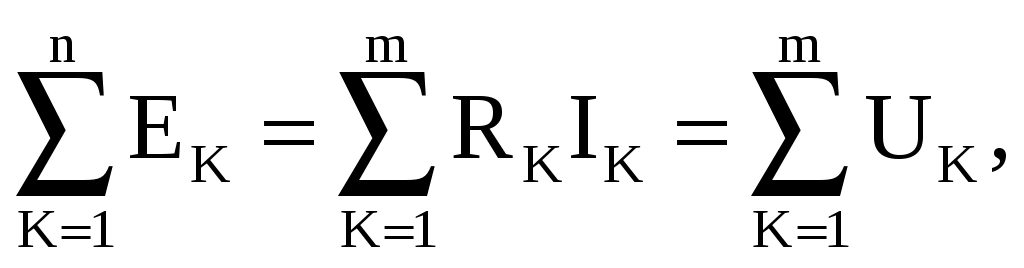



где n – число источников ЭДС в контуре; m – число элементов с сопротивлением R_к в контуре; U_к = R_кI_к – напряжение или падение напряжения на к-том элементе контура.

Для схемы (рис. 2.2) запишем уравнение по второму закону Кирхгофа:

E = U_R + U_2..

Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контура, включая источники ЭДС, равна нулю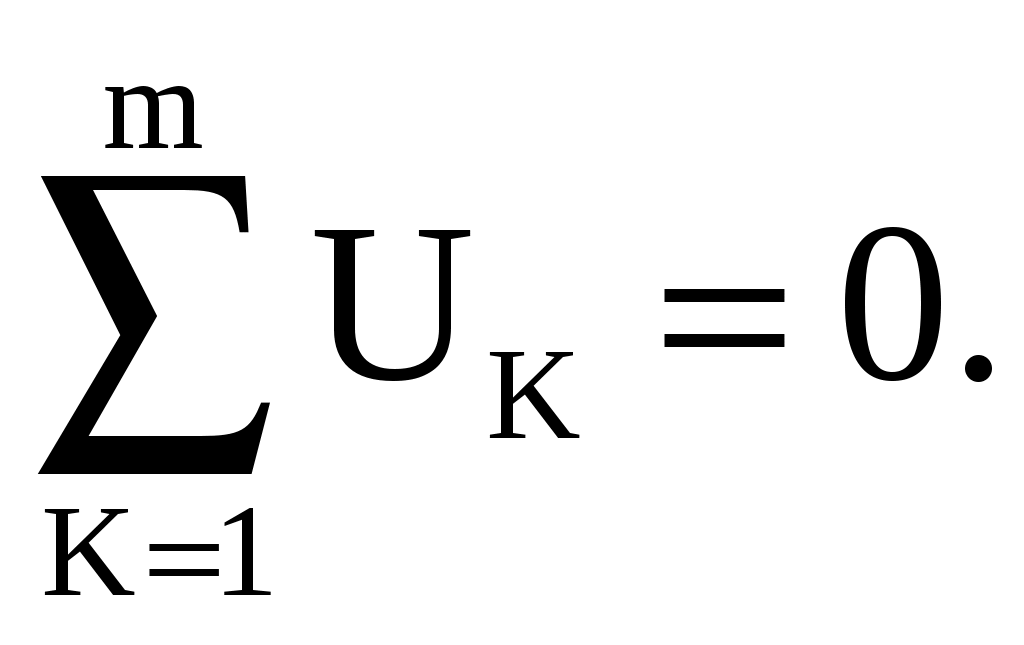



При записи уравнений по второму закону Кирхгофа необходимо:

1. задать условные положительные направления ЭДС, токов и напряжений;

2. выбрать направление обхода контура, для которого записывается уравнение;

3. записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.

Запишем уравнения по II закону Кирхгофа для контуров электрической схемы (рис. 2.2):

контур I: E = RI + R₁I₁ + r₀I,

контур II: R₁I₁ + R₂I₂ = 0,

контур III: E = RI + R₂I₂ + r₀I.

В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия

W = RI²t.

Скорость преобразования электрической энергии в другие виды представляет электрическую мощность



Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемых на всех участках цепи

(2.1)

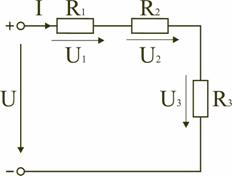
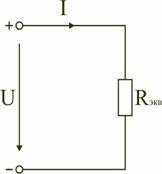
Соотношение (2.1) называют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение E I подставляют в (2.1) со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электрической энергии, и произведение E I подставляют в (2.1) со знаком минус. Для цепи, показанной на рис. 2.2 уравнение баланса мощностей запишется в виде:

EI = (r₀ + R) I²+ R₁I₁² + R₂I₂².

При расчете электрических цепей используются определенные единицы измерения. Электрический ток измеряется в амперах (А); напряжение – в вольтах (В); сопротивление – в омах (Ом); мощность – в ваттах (Вт); электрическая энергия – ватт-час (Вт-час); проводимость – в сименсах (См).

Кроме основных единиц используют более мелкие и более крупные единицы измерения: миллиампер (1 мA = 10^–3 А), килоампер (1 кA = 10³ А), милливольт (1 мВ = 10^–3В), киловольт (1 кВ = 10³ В), килоом (1 кОм = 10 ³ Ом), мегаом (1 МОм = 10 ⁶ Ом), киловатт (1 кВт = 10 ³ Вт), киловатт-час (1 кВт-час = 10³ ватт-час).

4. Способы соединения сопротивлений и расчет эквивалентного сопротивления электрической цепи

Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением R_экв, и вся схема представляется в виде схемы на рис. 2.5, где R=R_экв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.

2.4.1. Электрическая цепь с последовательным соединением элементов

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 2.4).

На основании второго закона Кирхгофа общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

U = U₁ + U₂ + U₃ или R_эквI = R₁I + R₂I + R₃I,

откуда следует

R_экв = R₁ + R₂ + R₃.

Рис. 2.4. Последовательное соединение	Рис. 2.5. Эквивалентная схема

Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R_экв (рис. 2.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома

I=U/ R_экв,

и по вышеприведенным формулам рассчитывают падение напряжений U₁, U₂, U₃ на соответствующих участках электрической цепи (рис. 2.4).

Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

2.4.2. Электрическая цепь с параллельным соединением элементов

Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 2.6).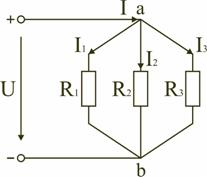


Рис. 2.6. Параллельное соединение элементов
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I₁ + I₂ + I₃, т.е.,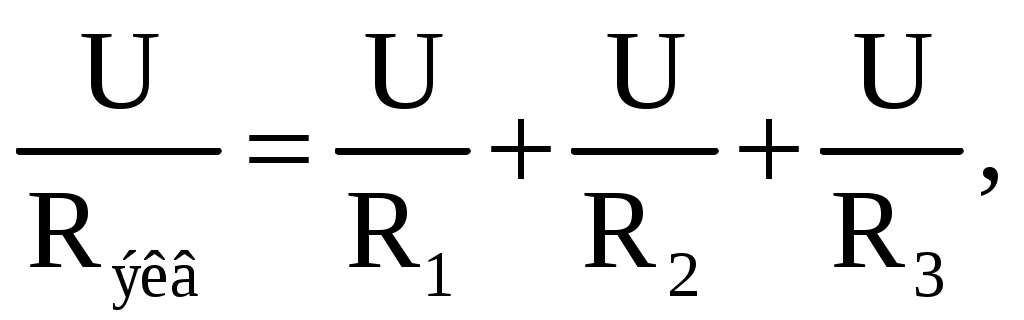



откуда следует, что

(2.2)

В том случае, когда параллельно включены два сопротивления R₁ и R₂, они заменяются одним эквивалентным сопротивлением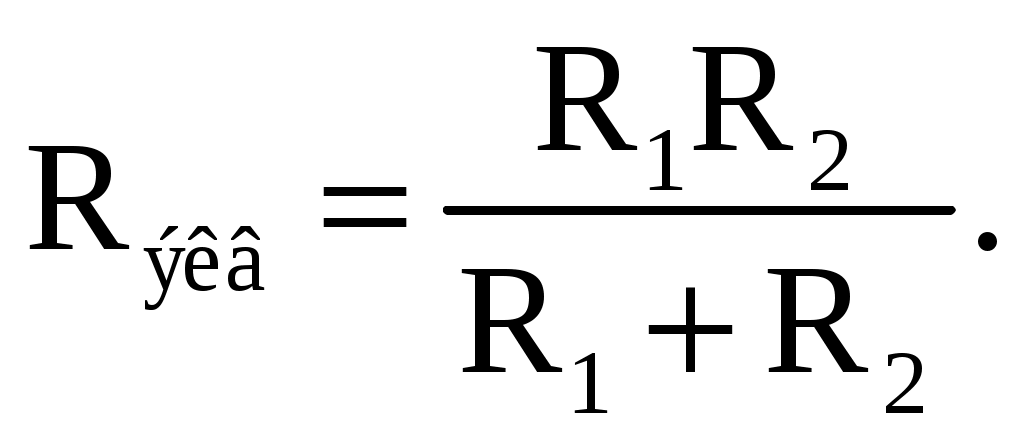



Из соотношения (2.2), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

g_экв = g₁ + g₂ + g₃.

По мере роста числа параллельно включенных потребителей проводимость цепи g_экв возрастает, и наоборот, общее сопротивление R_экв уменьшается.

Напряжение в электрической цепи с параллельно соединенными сопротивлениями

U = R_эквI = R₁I₁ = R₂  I₂= R₃I₃.

Отсюда следует, что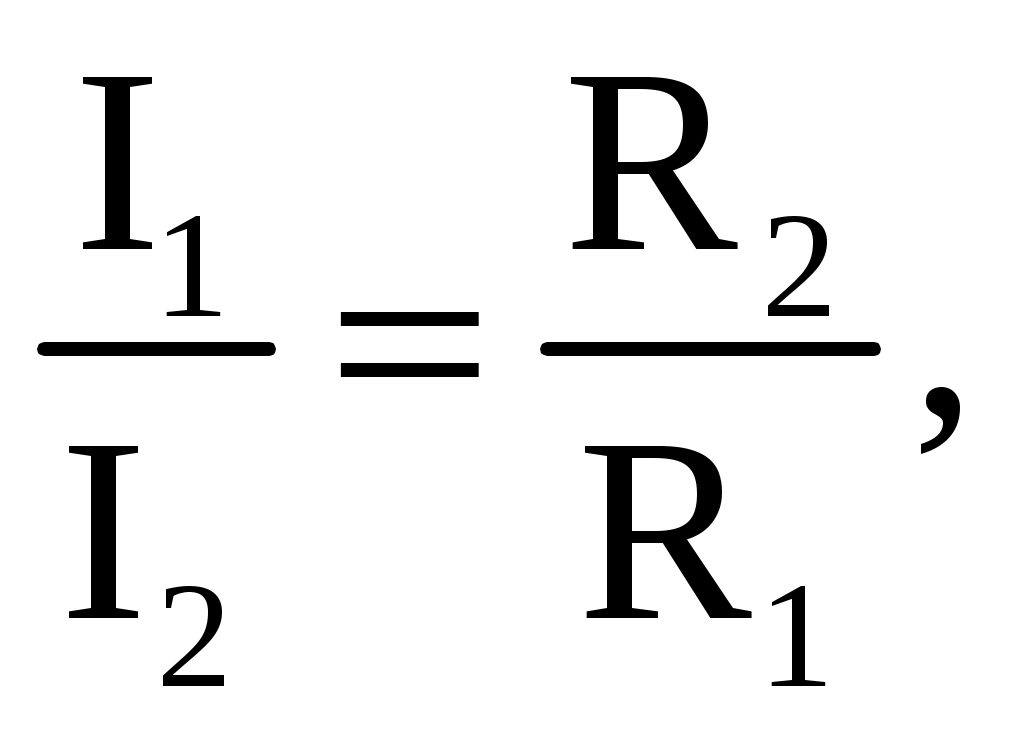



т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельной схеме включения работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

2.4.3. Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Для цепи, представленной на рис. 2.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R₁=R₂=R₃=R₄=R₅=R.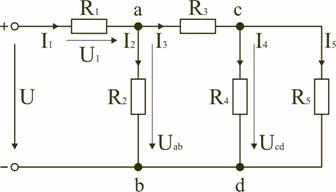



Рис. 2.7. Смешанное соединение элементов
Сопротивления R₄ и R₅ включены параллельно, тогда сопротивление участка цепи cd равно: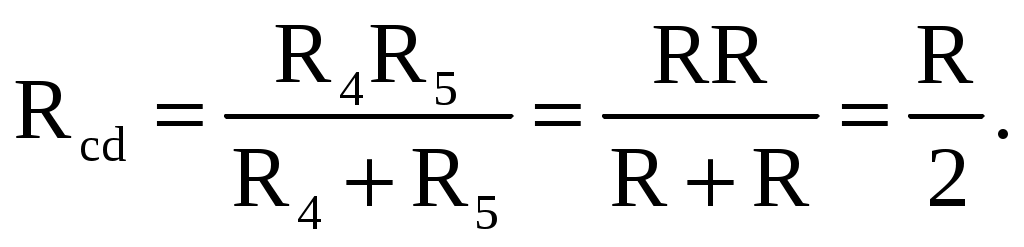



В этом случае исходную схему (рис. 2.7) можно представить в следующем упрощенном виде (рис. 2.8):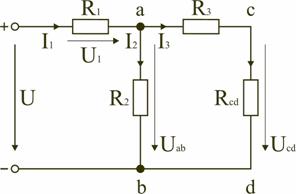

Рис. 2.8. Упрощенная схема 1
На схеме (рис. 2.8) сопротивление R₃ и R_cd соединены последовательно, и тогда сопротивление участка цепи ad равно:



Тогда схему (рис. 2.8) можно представить в упрощенном варианте 2 (рис.2.9). На схеме (рис. 2.9) сопротивление R₂ и R_ad соединены параллельно, тогда сопротивление участка цепи аb равно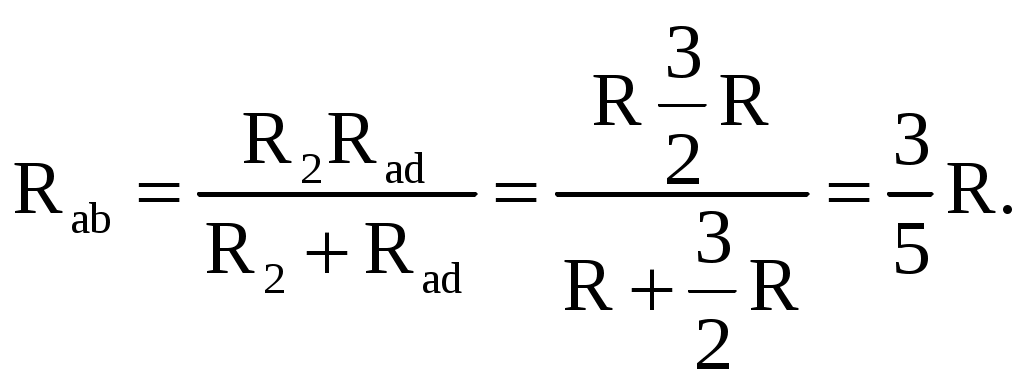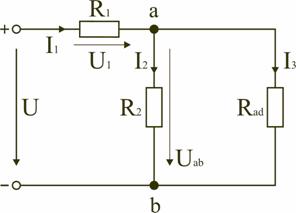





Рис. 2.9. Упрощенная схема 2
Схему (рис. 2.9) можно представить в упрощенном варианте 3 (рис. 2.10), где сопротивления R₁ и R_ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 2.7) будет равно: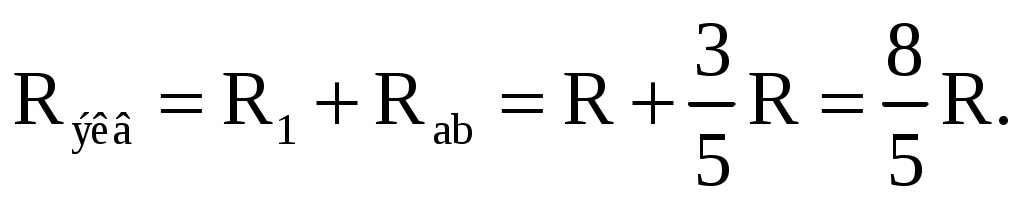



В результате преобразований исходная схема (рис. 2.7) представлена в виде схемы (рис. 2.11) с одним сопротивлением R_экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

Рис. 2.10. Упрощенная схема 3

Рис. 2.11. Упрощенная схема 4

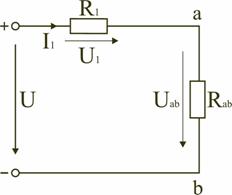
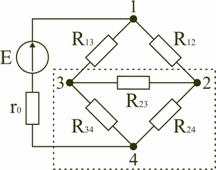
2.4.4. Соединение элементов электрической цепи по схемам «звезда» и «треугольник»

В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 2.12). Сопротивления R₁₂, R₁₃, R₂₄, R₃₄ включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–2 называется измерительной диагональю моста.

Рис. 2.12. Мостовая схема

Рис. 2.13. Схема соединения «звезда»

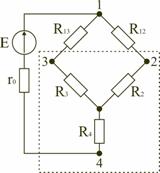
В мостовой схеме сопротивления R₁₃, R₁₂, R₂₃ и R₂₄, R₃₄, R₂₃ соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R₂₄ R₃₄ R₂₃ звездой R₂ R₃ R₄ (рис. 2.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям: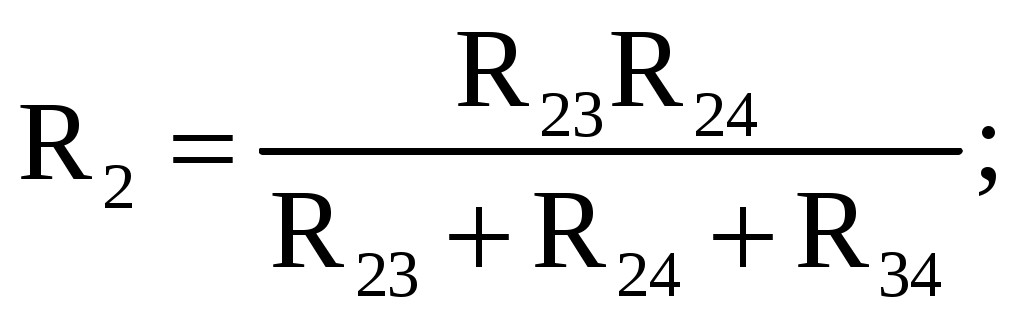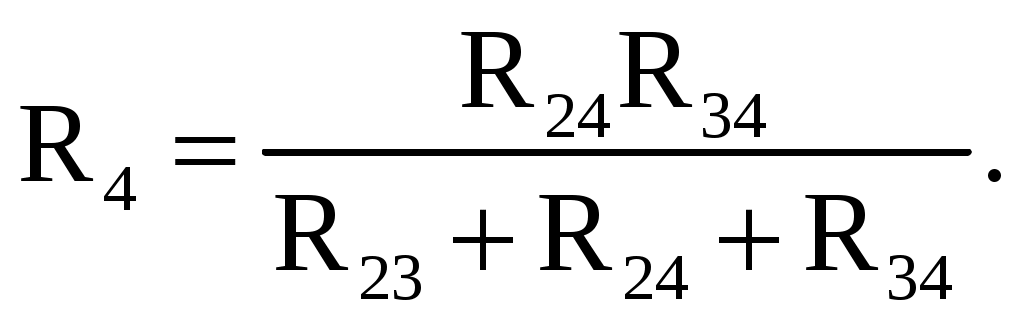



Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника: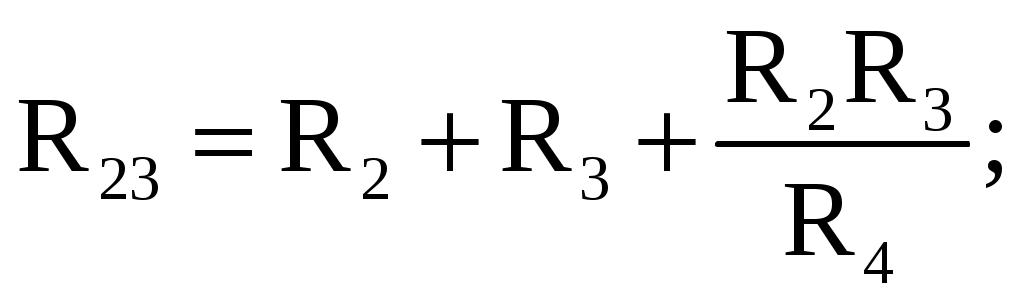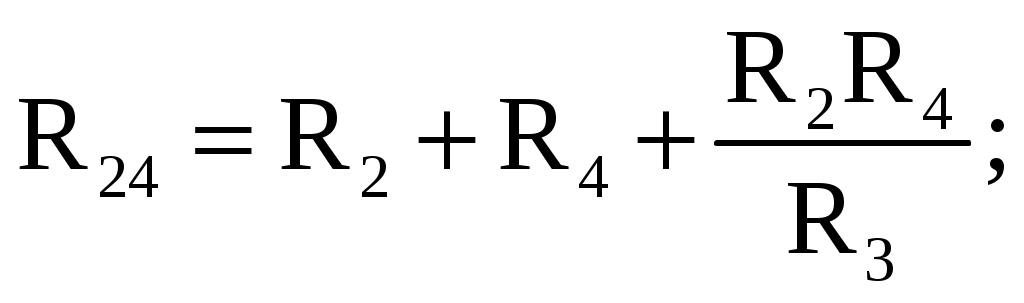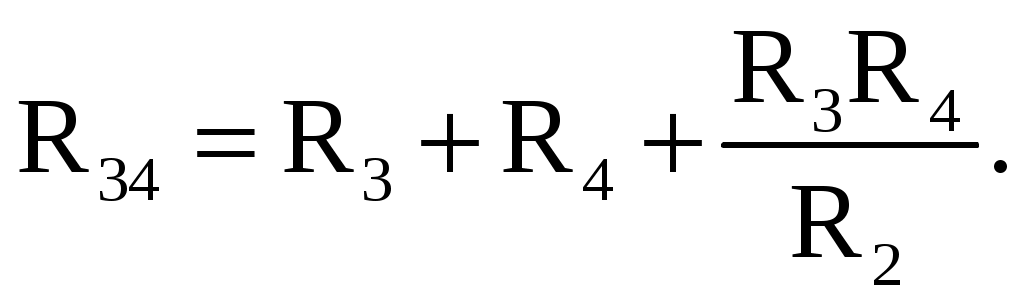



После проведенных преобразований (рис. 2.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 2.12)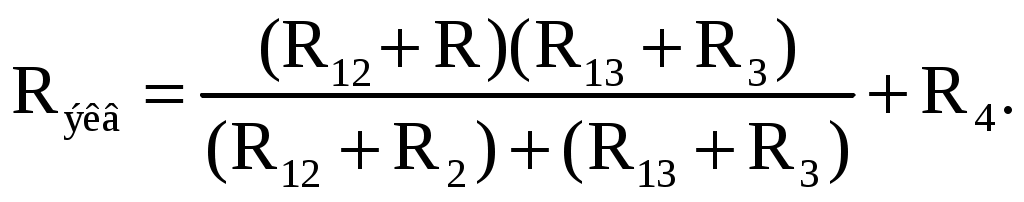


5. Источник ЭДС и источник тока в электрических цепях
При расчете и анализе электрических цепей реальный источник электрической энергии с конечным значением величины внутреннего сопротивления r₀ заменяют расчетным эквивалентным источником ЭДС или источником тока.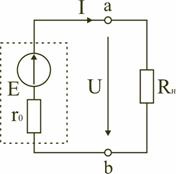


Рис. 2.14. Схема с источником ЭДС
Источник ЭДС (рис. 2.14) имеет внутреннее сопротивление r₀, равное внутреннему сопротивлению реального источника. Стрелка в кружке указывает направление возрастания потенциала внутри источника ЭДС. Для данной цепи запишем соотношение по второму закону Кирхгофа

E = U + r₀I или U = E − r₀I.

Зависимость напряжения U на зажимах реального источника от тока I определяется его вольт-амперной или внешней характеристикой (рис. 2.15). Уменьшение напряжения источника U при увеличении тока нагрузки I объясняется падением напряжения ΔU=Ir₀ на его внутреннем сопротивлении r₀.

Рис. 2.15. Внешняя характеристика источника ЭДС	Рис. 2.16. Внешняя характеристика идеального источника ЭДС

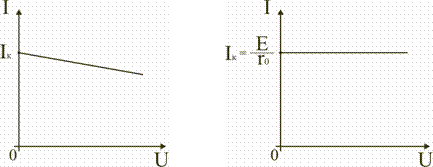
У идеального источника ЭДС внутреннее сопротивление r₀ << R_н (приближенно r₀ ≈0). В этом случае его вольт-амперная характеристика представляет собой прямую линию (рис. 2.16), следовательно, напряжение U на его зажимах постоянно (U=E) и не зависит от величины сопротивления нагрузки R_н.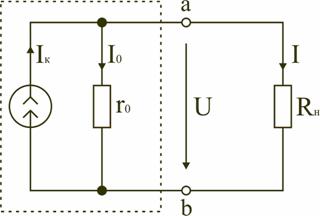

Рис. 2.17. Схема с источником тока
Источник тока, заменяющий реальный источник электрической энергии, характеризуется неизменным по величине током I_к, равным току короткого замыкания источника ЭДС I_к =E/ r₀, и внутренним сопротивление r₀, включенным параллельно (рис. 2.17).

Стрелка в кружке указывает положительное направление тока источника. Для данной цепи запишем соотношение по первому закону Кирхгофа

I_к = I₀ + I;. I₀ = U/r₀.

В этом случае вольт-амперная (внешняя) характеристика I(U) источника тока определится соотношением

I = I_к − I₀ = I_к − U/r₀

и представлена на рис. 2.18.

Рис. 2.18. Внешняя характерис- тика реального источника тока	Рис. 2.19. Внешняя характеристика идеального источника тока

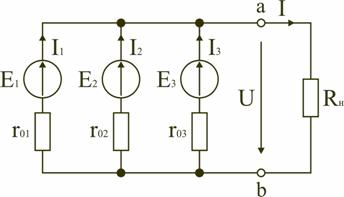
Уменьшение тока нагрузки I при увеличении напряжения U на зажимах ab источника тока, объясняется увеличением тока I₀, замыкающегося в цепи источника тока.

В идеальном источнике тока r₀>>R_н. В этом случае можно считать, что при изменении сопротивления нагрузки R_н потребителя I₀≈0, а I≈I_к. Тогда вольт-амперная характеристика I(U) идеального источника тока представляет прямую линию, проведенную параллельно оси абсцисс на уровне I = I_к = E/r₀ (рис. 2.19).

При сравнении внешних характеристик источника ЭДС (рис. 2.15) и источника тока (рис. 2.18) следует, что они одинаково реагируют на изменение величины сопротивления нагрузки. Покажем, что в обоих случаях ток I в нагрузке определяется одинаковым соотношением.

Ток в нагрузке R_н для схем источника ЭДС (рис. 2.14) и источника тока (рис. 2.17) одинаков и равен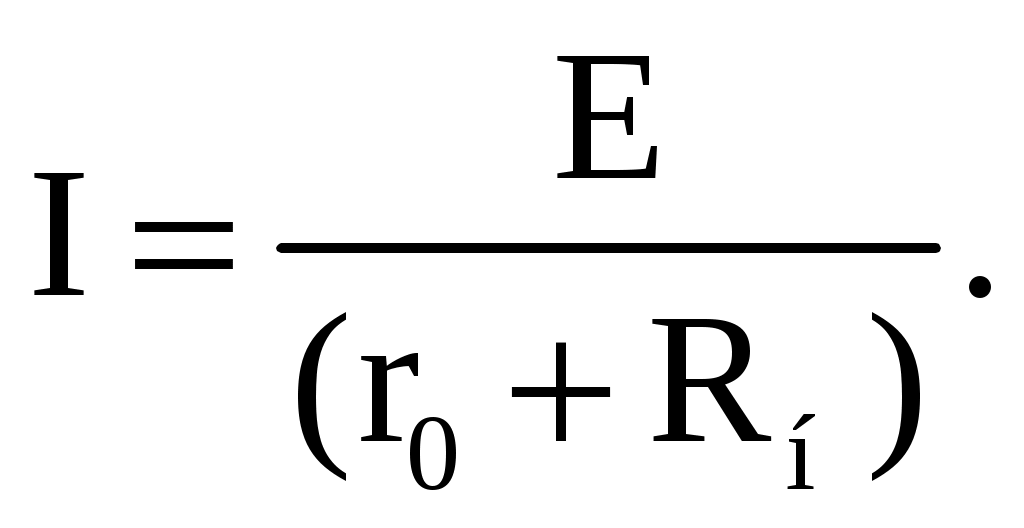



Для схемы рис. 2.14 это следует из закона Ома, т.к. при последовательном соединении сопротивления r₀ и R_н складываются. В схеме рис. 2.17 ток 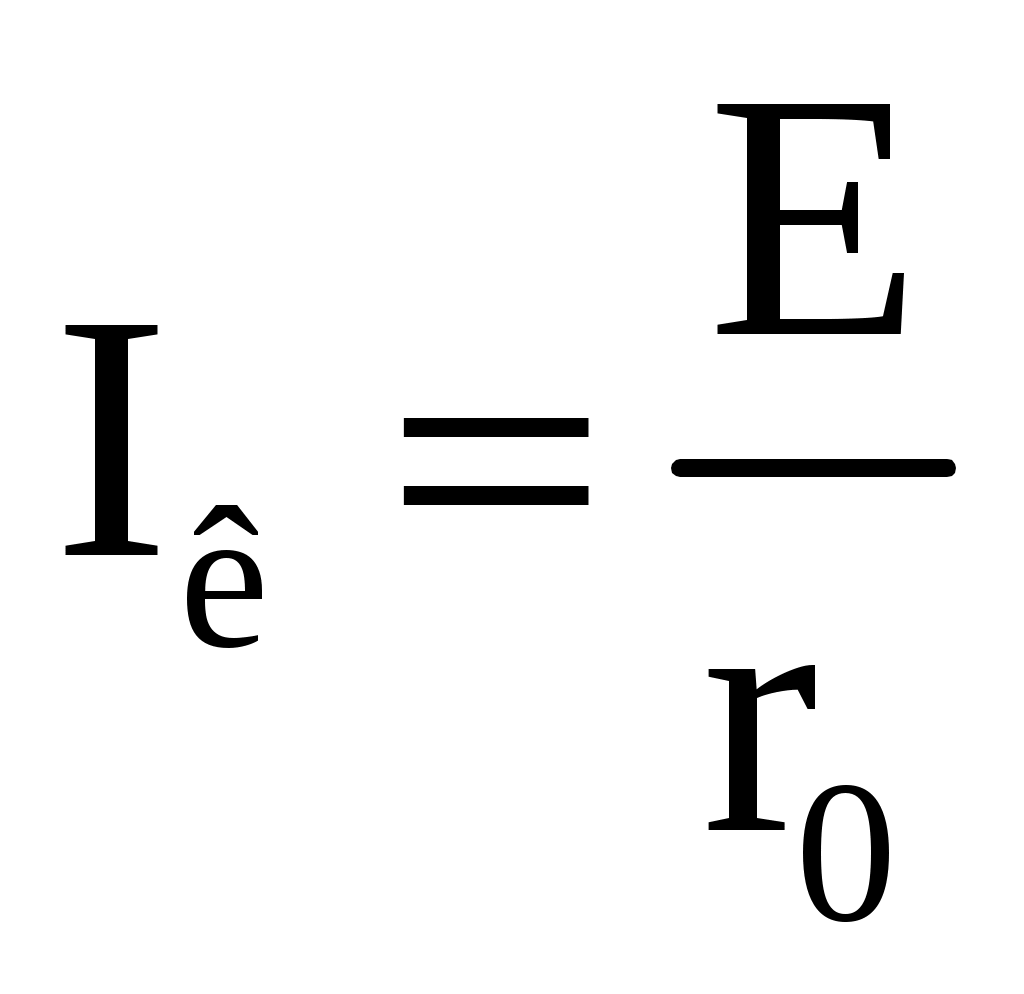распределяется обратно пропорционально сопротивлениям r₀ и R_н двух параллельных ветвей. Ток в нагрузке R_н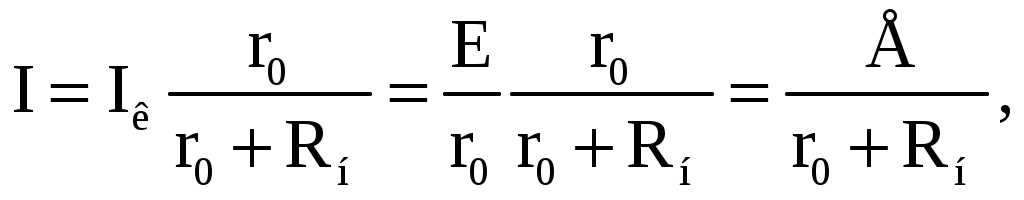



т.е. совпадает по величине с током при подключении нагрузки к источнику ЭДС. Следовательно, схема источника тока (рис. 2.17) эквивалентна схеме источника ЭДС (рис. 2.14) в отношении энергии, выделяющейся в сопротивлении нагрузки R_н, но не эквивалентна ей в отношении энергии, выделяющейся во внутреннем сопротивлении источника питания.

Каким из двух эквивалентных источников питания пользоваться, не играет существенной роли. Однако на практике, особенно при расчете электротехнических устройств, чаще используется в качестве источника питания источник ЭДС с внутренним сопротивлением r₀ и величиной электродвижущей силы Е.

В тех случаях, когда номинальное напряжение или номинальный ток и мощность источника электрической энергии оказываются недостаточными для питания потребителей, вместо одного используют несколько источников. Существуют два основных способа соединения источников питания: последовательное и параллельное.

Последовательное включение источников питания (источников ЭДС) применяется тогда, когда требуется создать напряжение требуемой величины, а рабочий ток в цепи меньше или равен номинальному току одного источника ЭДС (рис. 2.20).

Для этой цепи на основании второго закона Кирхгофа можно записать

E₁ + E₂ + E₃ = (r₀₁ + r₀₂ + r₀₃ + R_н) I.

Откуда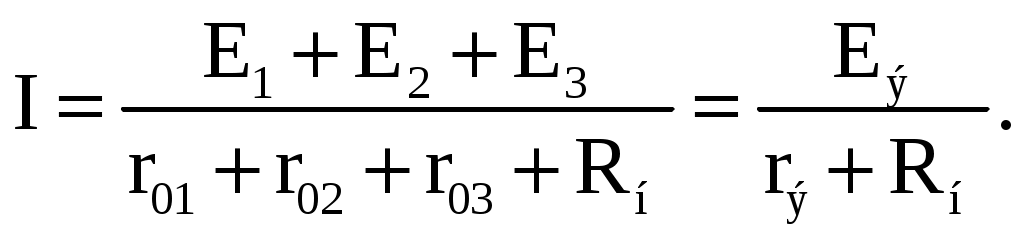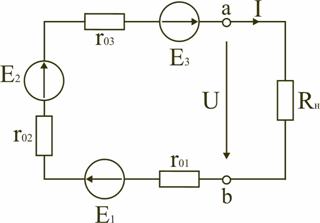




Рис. 2.20. Последовательное включение источников ЭДС
Таким образом, электрическая цепь на рис. 2.20 может быть заменена цепью с эквивалентным источником питания (рис. 2.21), имеющим ЭДС E_э и внутреннее сопротивление r_э.

При параллельном соединении источников (рис. 2.22) соединяются между собой положительные выводы всех источников, а также их отрицательные выводы. Характерным для параллельного соединения является одно и то же напряжение U на выводах всех источников. Для электрической цепи на рис. 2.22 можно записать следующие уравнения:

I = I₁ + I₂ + I₃; P = P₁ + P₂ + P₃ = UI₁ + UI₂ + UI₃ = UI.

Рис. 2.21. Схема с эквивалентным источником питания

Рис. 2.22. Схема с параллельным соединением источников

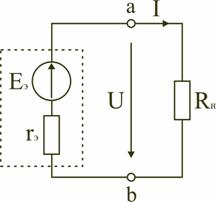
Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей источников. Параллельное соединение источников применяется в первую очередь тогда, когда номинальные ток и мощность одного источника недостаточны для питания потребителей.

На параллельную работу включают обычно источники с одинаковыми ЭДС, мощностями и внутренними сопротивлениями.
6. Режимы работы электрической цепи

При подключении к источнику питания различного количества потребителей или изменения их параметров будут изменяться величины напряжений, токов и мощностей в электрической цепи, от значений которых зависит режим работы цепи и ее элементов.

Реальная электрическая цепь может быть представлена в виде активного и пассивного двухполюсников (рис. 2.23).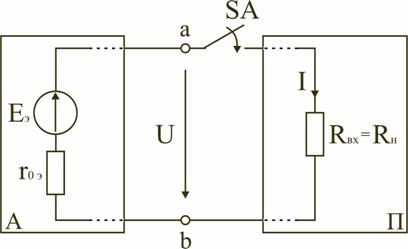



Рис. 2.23. Схема соединения в виде двухполюсников
Двухполюсником называют цепь, которая соединяется с внешней относительно нее частью цепи через два вывода а и b – полюса.

Активный двухполюсник содержит источники электрической энергии, а пассивный двухполюсник их не содержит. Для расчета цепей с двухполюсниками реальные активные и пассивные элементы цепи представляются схемами замещения. Схема замещения пассивного двухполюсника П представляется в виде его входного сопротивления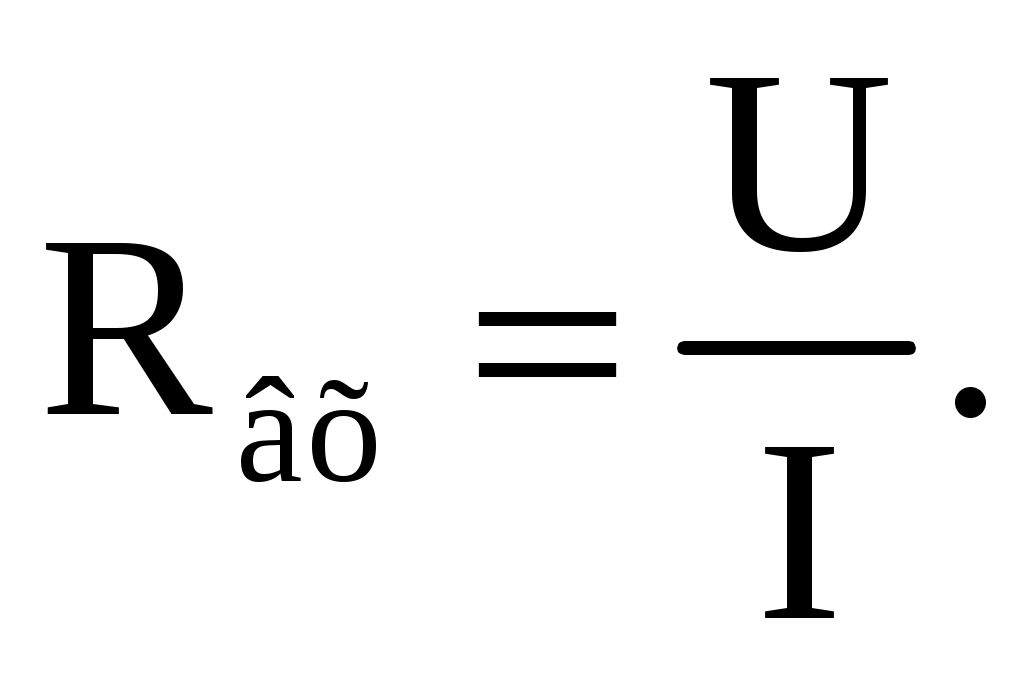



Схема замещения активного двухполюсника А представляется эквивалентным источником с ЭДС E_э и внутренним сопротивлением r_0э, нагрузкой для которого является входное сопротивление пассивного двухполюсника R_вх = R_н.

Режим работы электрической цепи (рис. 2.23) определяется изменениями параметров пассивного двухполюсника, в общем случае величиной сопротивления нагрузки R_н. При анализе электрической цепи рассматривают следующие режимы работы: холостого хода, номинальный, короткого замыкания и согласованный.

Работа активного двухполюсника под нагрузкой R_н определяется его вольт-амперной (внешней) характеристикой, уравнение которой для данной цепи запишется в виде

U = E − r0эI.

(2.3)

Эта вольт-амперная характеристика строится по двум точкам 1 и 2 (рис. 2.24), соответствующим режимам холостого хода и короткого замыкания.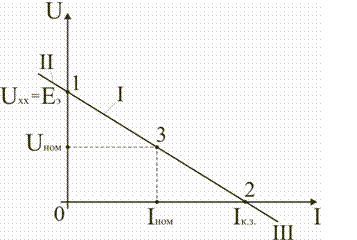



Рис. 2.24. Внешняя характеристика
2.6.1. Режим холостого хода

В этом режиме с помощью ключа SA нагрузка R_н отключается от источника питания (рис. 2.23). В этом случае ток в нагрузке становится равным нулю, и как следует из соотношения (2.14) напряжение на зажимах ab становится равным ЭДС E_э и называется напряжением холостого хода U_хх

U = U_хх = E_э.

2.6.2. Режим короткого замыкания

В этом режиме ключ SA в схеме электрической цепи (рис. 2.23) замкнут, а сопротивление R_н=0.

В этом случае напряжение U на зажимах аb становится равным нулю, т.к. U = R_нI, а уравнение (2.3) вольт-амперной характеристики можно записать в виде



Значение тока короткого замыкания I_кз соответствует т.2 на вольт-амперной характеристике (рис. 2.24).

Анализ этих двух режимов показывает, что при расчете электрических цепей параметры активного двухполюсника E_э и r_0э могут быть определены по результатам режимов холостого хода и короткого замыкания:

E_э= U_хх и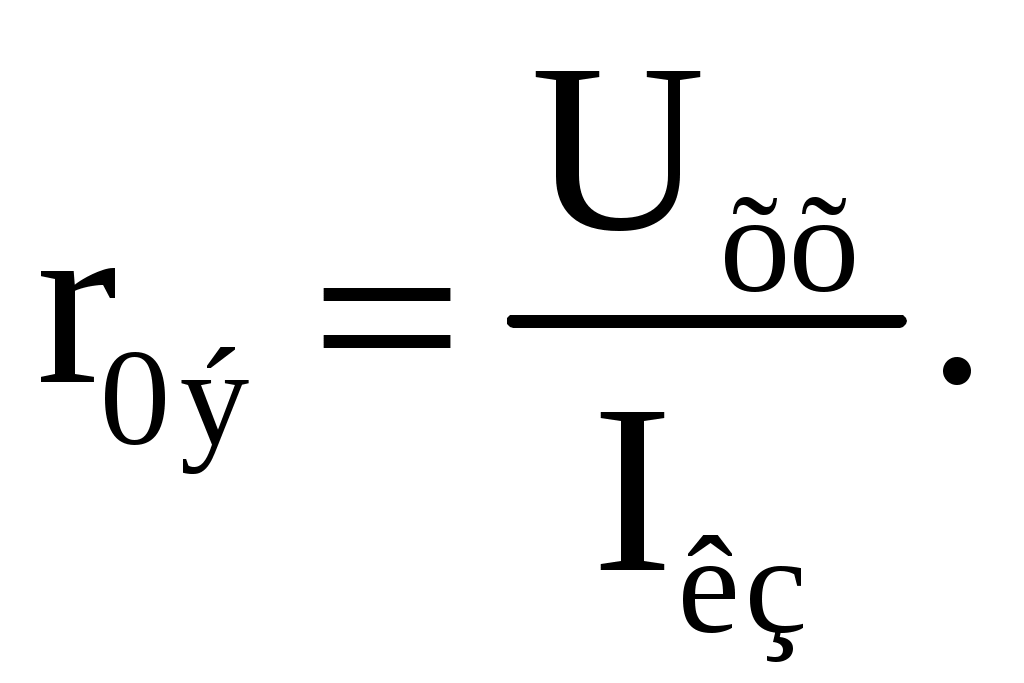

При изменении тока в пределах 0 ≤I ≤I_к активной двухполюсник (эквивалентный источник) отдает энергию во внешнюю цепь (участок I вольт-амперной характеристики на рис. 2.24). При токе I<0 (участок II) источник получает энергию из внешней цепи, т.е. работает в режиме потребителя электрической энергии. Это произойдет, если к зажимам аb двухполюсника присоединена внешняя цепь с источниками питания. При напряжении U<0 (участок III) резисторы активного двухполюсника потребляют энергию источников из внешней цепи и самого активного двухполюсника.

2.6.3. Номинальный режим

Номинальный режим электрической цепи обеспечивает технические параметры как отдельных элементов, так и всей цепи, указанные в технической документации, в справочной литературе или на самом элементе. Для разных электротехнических устройств указывают свои номинальные параметры. Однако три основных параметра указываются практически всегда: номинальное напряжение U_ном, номинальная мощность Р_ном и номинальный ток I_ном.

Работа активного двухполюсника под нагрузкой в номинальном режиме определяется уравнением (2.3), записанном для номинальных параметров

U_ном = E_э − r_0эI_ном.

На вольт-амперной характеристике (рис. 2.24) это уравнение определяется точкой 3 с параметрами

U_ном и I_ном.

2.6.4. Согласованный режим

Согласованный режим электрической цепи обеспечивает максимальную передачу активной мощности от источника питания к потребителю. Определим параметры электрической цепи (рис. 2.23), обеспечивающие получение согласованного режима. При подключении нагрузки R_н к активному двухполюснику (рис. 2.23) в ней возникает ток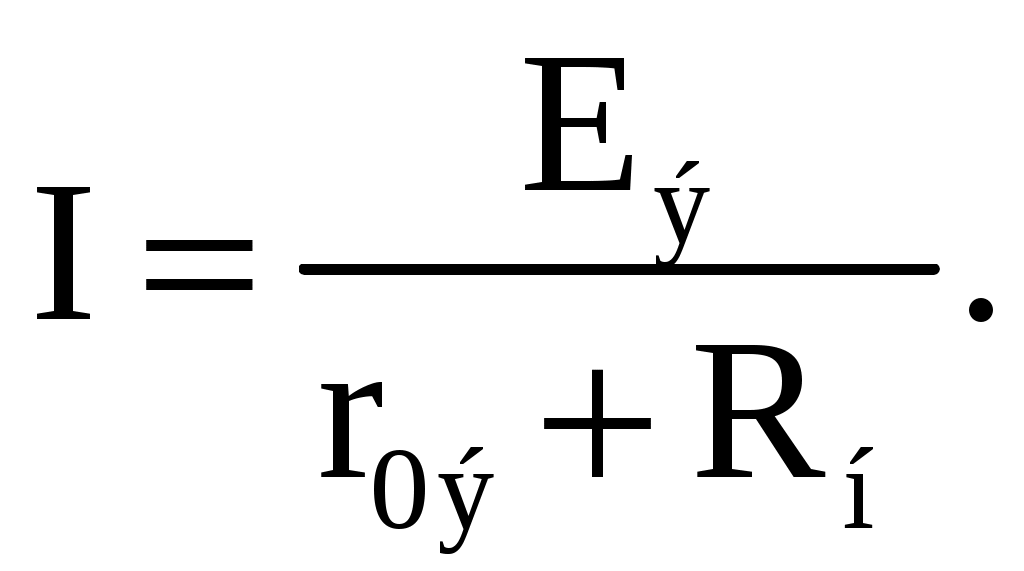



При этом на нагрузке выделится активная мощность

(2.4)

Определим соотношение между сопротивлением нагрузки R_н и внутренним сопротивлением r_0э эквивалентного источника ЭДС, при котором в сопротивлении нагрузки R_н выделяется максимальная мощность при неизменных значениях E_э и r_0э. С этой целью определим первую производную Р по R_н и приравняем ее к нулю: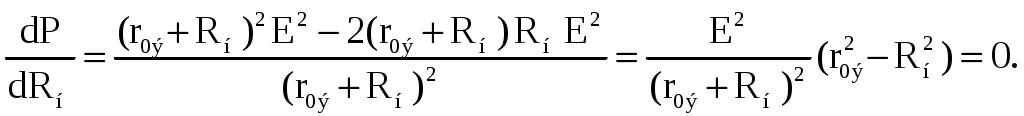



Так как выражение в знаменателе – конечное, то, отбрасывая не имеющее физического смысла решение R_н = -r_0э, получим, что значение сопротивления нагрузки, согласованное с сопротивлением источника

Rн = r0э

(2.5)

Можно найти вторую производную и убедиться в том, что она отрицательна 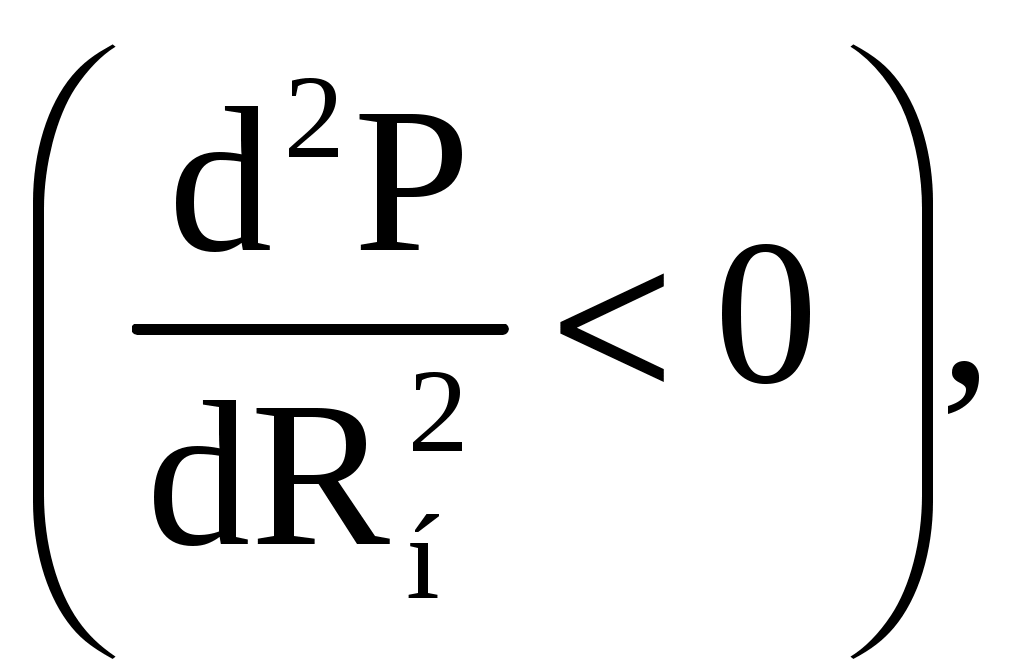поэтому соотношение (2.5) соответствует максимуму функции P = F(R_н).

Подставив (2.5) в (2.4), получим значение максимальной мощности, которая может быть выделена в нагрузке R_н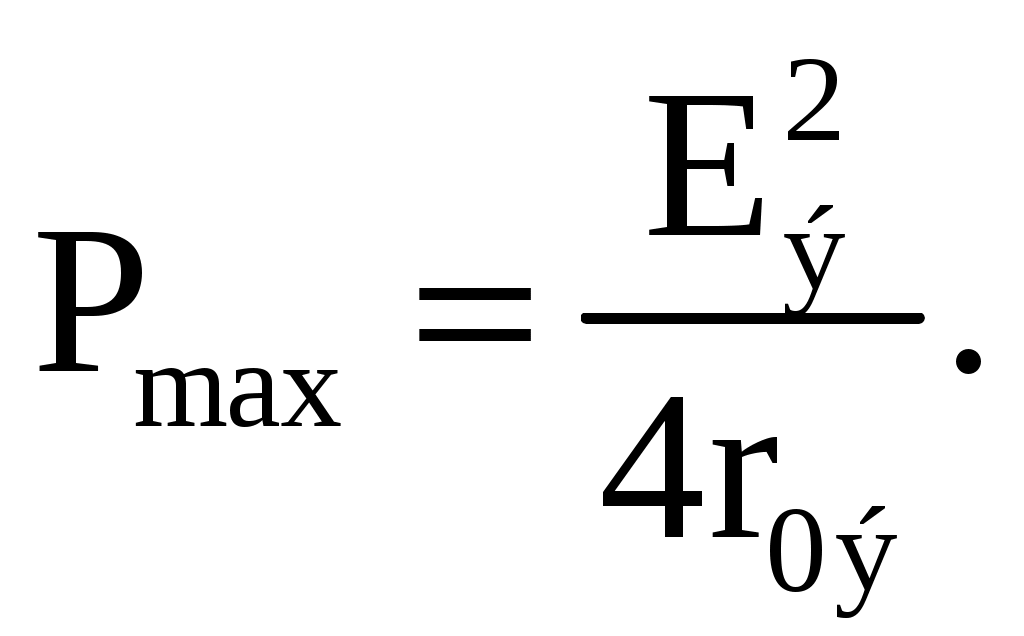



Полезная мощность, выделяемая в нагрузке, определяется уравнением (2.4). Полная активная мощность, выделяемая активным двухполюсником,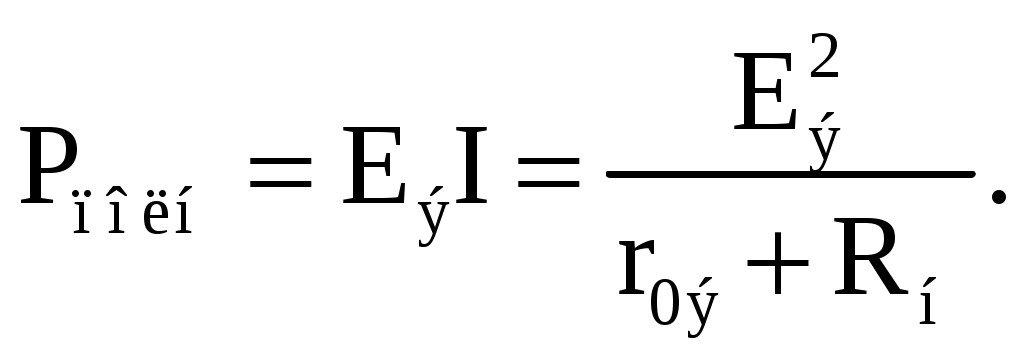

Коэффициент полезного действия



если R_н = r_0э, то КПД=0,5.

Для мощных электротехнических устройств такое низкое значение КПД недопустимо. Но в электронных устройствах и схемах, где величина Р измеряется в милливаттах, с низким КПД можно не считаться, поскольку в этом режиме обеспечивается максимальная передача мощности на нагрузку.
7. Расчет электрических цепей с использованием законов