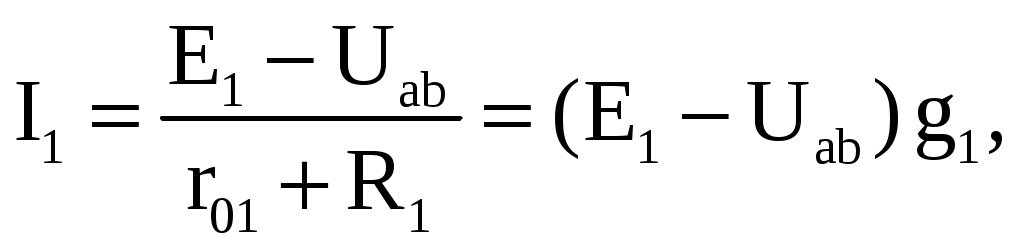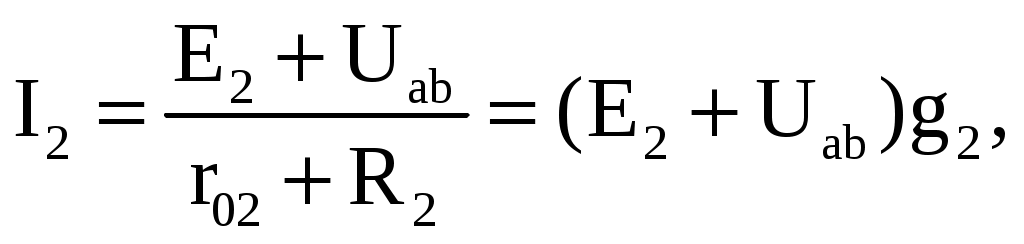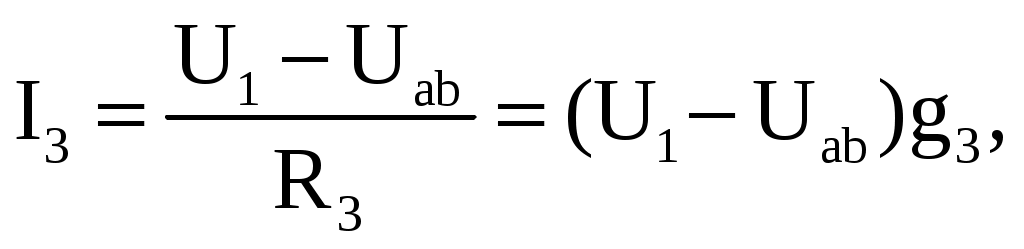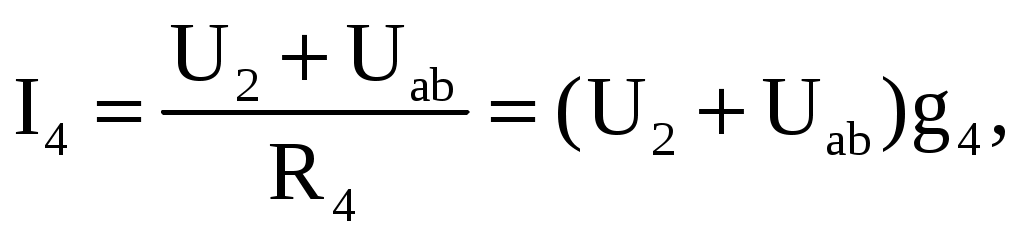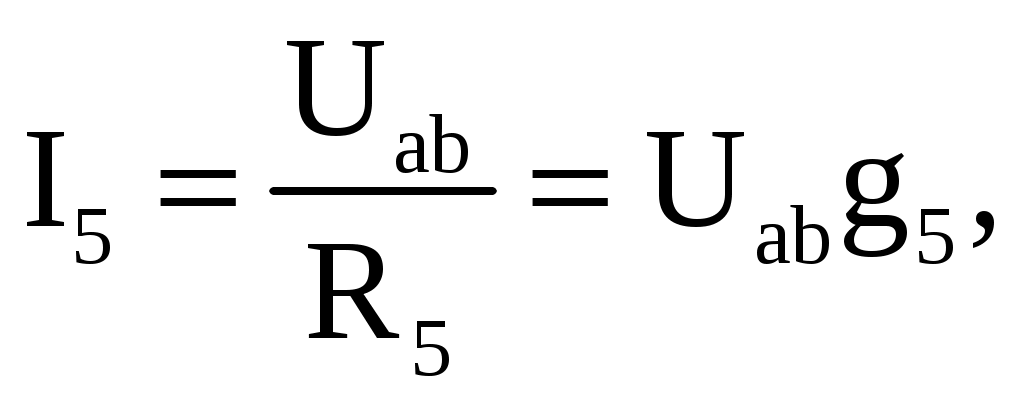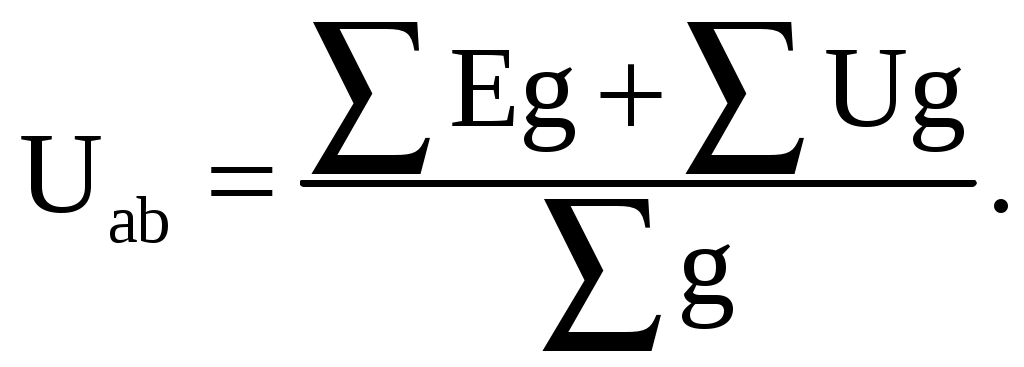ПОСТ ЛЕКЦИИ(1). Электрические цепи постоянного тока и методы их расчета электрическая цепь и ее элементы

• Название: Электрические цепи постоянного тока и методы их расчета электрическая цепь и ее элементы
• Дата: 03.10.2021
• Размер: 0.52 Mb.
• Имя файла: ПОСТ ЛЕКЦИИ(1).doc
• Тип: Задача; #240736
• страница: 2 из 2

Ома и Кирхгофа

Законы Ома и Кирхгофа используют, как правило, при расчете относительно простых электрических цепей с небольшим числом контуров, хотя принципиально с их помощью можно рассчитать сколь угодно сложные электрические цепи. При расчете электрических цепей в большинстве случаев известны параметры источников ЭДС или напряжения, сопротивления элементов электрической цепи, и задача сводится к определению токов в ветвях цепи. Зная токи, можно найти напряжения на элементах цепи, мощность, потребляемую отдельными элементами и всей цепью в целом, мощность источников питания и др.

7.1. Расчет цепи с одним источником питания

Электрическая цепь, схема которой приведена на рис. 2.25, состоит из одного источника питания, имеющего ЭДС E и внутреннее сопротивление r₀, и резисторов R₁, R₂, R₃, подключенных к источнику по смешанной схеме. Операции расчета такой схемы рекомендуется производить в определенной последовательности.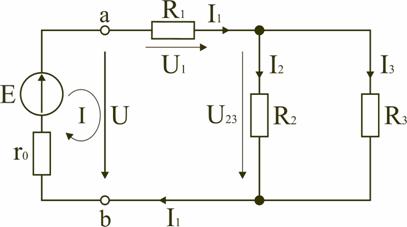


Рис. 2.25. Расчетная схема электрической цепи
1. Задание токов и напряжений на участках цепи.

Резистор R₁ включен последовательно с источником, поэтому ток I₁ для них будет общим, токи в резисторах R₂ и R₃ обозначим соответственно I₂ и I₃. Аналогично обозначим напряжения на участках цепи.

2. Расчет эквивалентного сопротивления цепи.

Резисторы R₂ и R₃ включены по параллельной схеме и заменяются эквивалентным сопротивлением: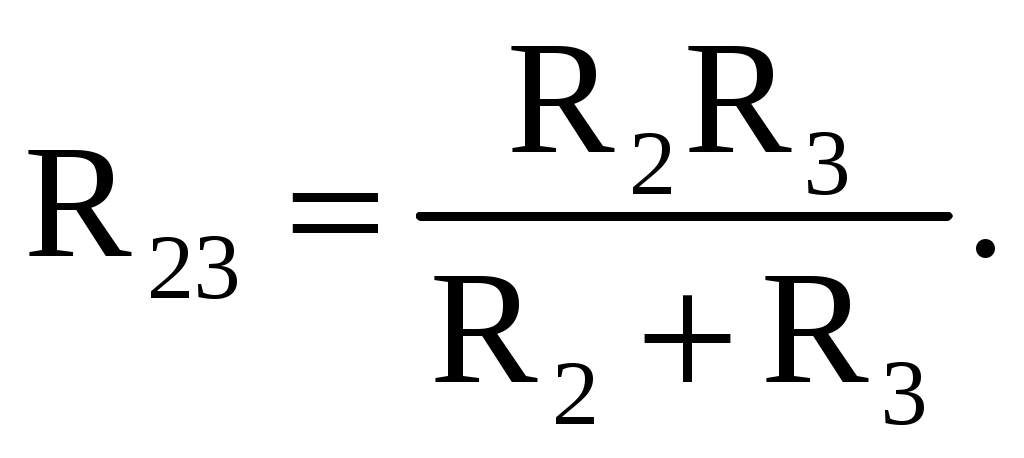



В результате цепь на рис. 2.25 преобразуется в цепь с последовательно соединенными резисторами R₁, R₂₃ и r₀. Тогда эквивалентное сопротивление всей цепи запишется в виде:

R_э = r₀ + R₁ + R₂₃.

3. Расчет тока в цепи источника.

Ток I₁ определим по закону Ома:

I₁ = U/R_э.

4. Расчет напряжений на участках цепи.

По закону Ома определим величины напряжений:

U₁ = R₁I₁; U₂₃ = R₂₃I₁.

Напряжение U на зажимах ab источника питания определим по второму закону Кирхгофа для контура I (рис. 2.25):

E = r₀I₁ + U; U = E − r₀I₁.

5. Расчет токов и мощностей для всех участков цепи.

Зная величину напряжения U₂₃, определим по закону Ома токи в резисторах R₂ и R₃: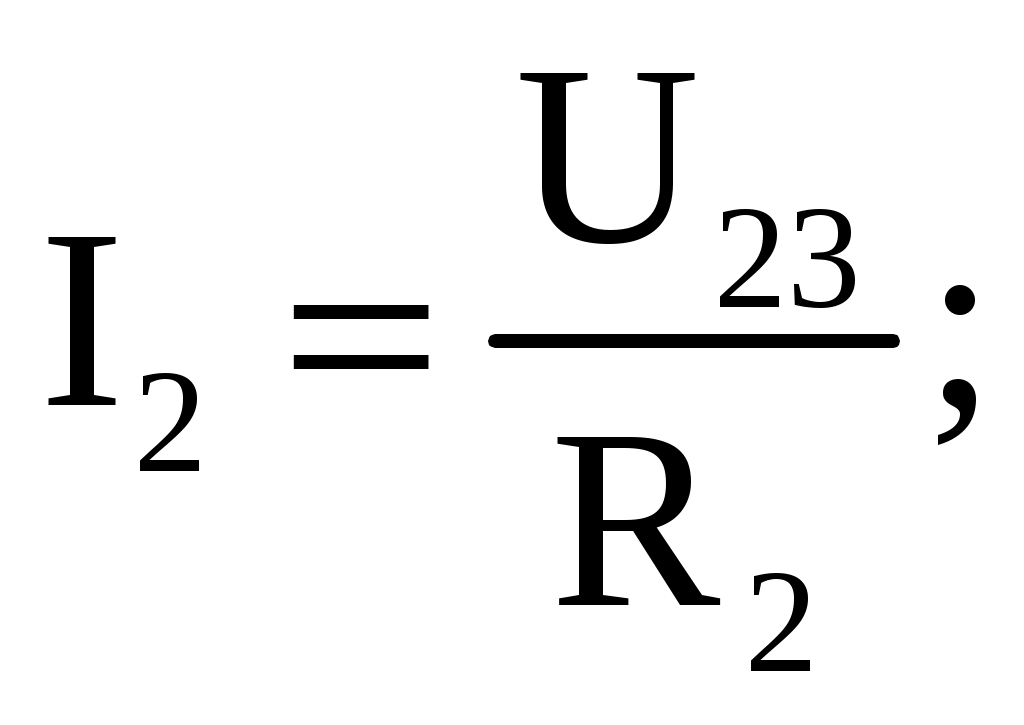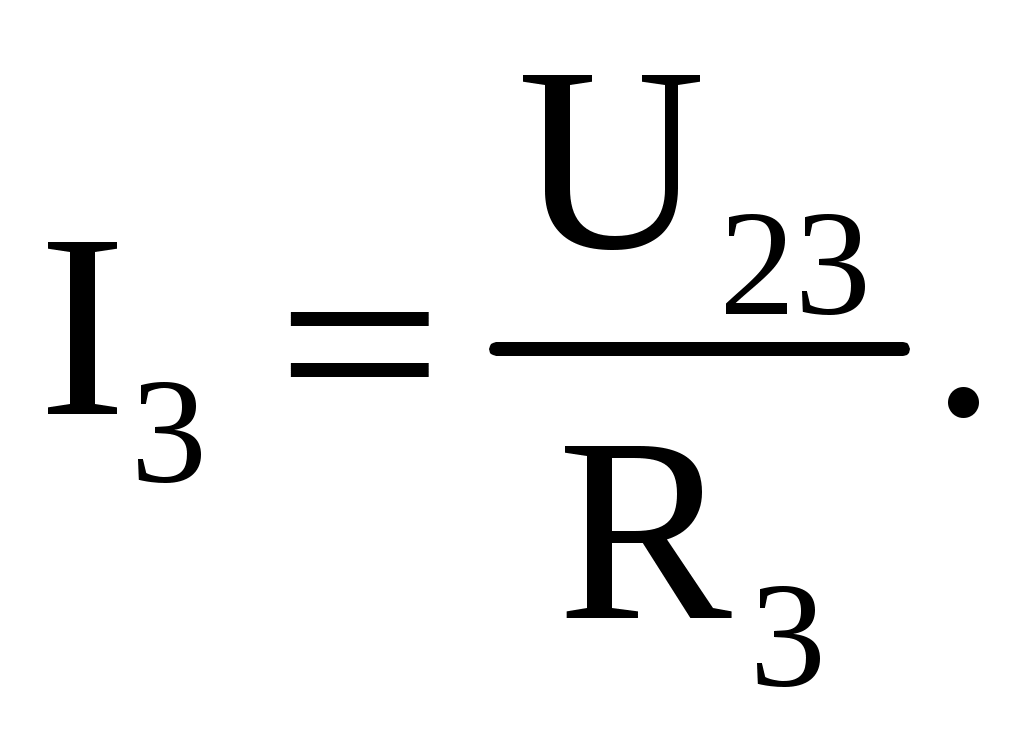



По формуле (2.1) определим величину активной электрической мощности, отдаваемую источником питания потребителям электрической энергии:

P = E∙I₁.

В элементах схемы расходуются активные мощности:



На внутреннем сопротивлении r₀ источника питания расходуется часть электрической мощности, отдаваемой источником. Эту мощность называют мощностью потерь ΔP:



6. Проверка правильности расчетов.

Эта проверка производится составлением уравнения баланса мощностей (2.1): мощность, отдаваемая источником питания, должна быть равна сумме мощностей, расходуемых в резистивных элементах схемы:



Кроме того, правильность вычисления токов можно проверить, составив уравнение по первому закону Кирхгофа для узла схемы:

I₁ = I₂ + I₃.
7.2. Расчет разветвленной электрической цепи с несколькими источниками питания

Основным методом расчета является метод непосредственного применения первого и второго законов Кирхгофа. В качестве примера рассмотрим цепь, схема которой приведена на рис. 2.26. Схема цепи содержит 6 ветвей (m=6) и 4 узла: a, b, c, d (n=4). По каждой ветви проходит свой ток, следовательно, число неизвестных токов равно числу ветвей, и для определения токов необходимо составить m уравнений. При этом по первому закону Кирхгофа составляют уравнения для (n–1) узлов. Недостающие m–(n–1) уравнения получают по второму закону Кирхгофа, составляя их для m–(n–1) взаимно независимых контуров. Рекомендуется выполнять операции расчета в определенной последовательности.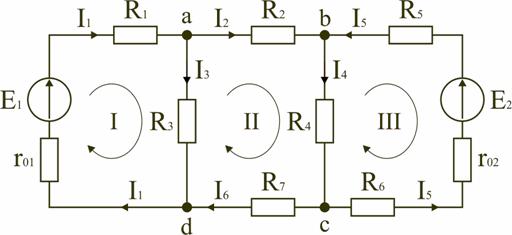


Рис. 2.26. Расчетная схема
1. Задание токов во всех ветвях.

Направление токов выбираем произвольно, но в цепях с источниками ЭДС рекомендуется, чтобы направление токов совпадало с направлением ЭДС.

2. Составление уравнений по первому закону Кирхгофа.

Выбираем 4–1=3 узла (a, b, c) и для них записываем уравнения:

узел a: I₁ − I₂ − I₃ = 0;

узел b: I₂ − I₄ + I₅ = 0;

узел c: I₄ − I₅ + I₆ = 0.

3. Составление уравнений по второму закону Кирхгофа.

Необходимо составить 6–3=3 уравнения. В схеме на рис. 2.26 выбираем контура I, II, III и для них записываем уравнения:

контур I: E₁ = (r₀₁ + R₁) I₁+ R₃I₃;

контур II: 0 = R₂I₂ + R₄I₄ + R₇I₆ − R₃I₃;

контур III: −E₂ = − (r₀₂ + R₅ + R₆)∙I₅ − R₄I₄.

4. Решение полученной системы уравнений и анализ результатов.

Полученная система из шести уравнений решается известными математическими методами. Если в результате расчетов численное значение тока получено со знаком «минус», это означает, что реальное направление тока данной ветви противоположно принятому в начале расчета. Если в ветвях с ЭДС токи совпадают по направлению с ЭДС, то данные элементы работают в режиме источников, отдавая энергию в схему. В тех ветвях, где направления тока и ЭДС не совпадают, источники ЭДС работает в режиме потребителя.


5. Проверка правильности расчетов.

Для проверки правильности произведенных расчетов можно на основании законов Кирхгофа написать уравнения для узлов и контуров схемы, которые не использовались при составлении исходной системы уравнений:

узел d:

I₃ + I₆ − I₁ = 0,

внешний контур схемы:

E₁ − E₂ = (r₀₁ + R₁) I₁ + R₂I₂ − (r₀₂ + R₅ +R₆) I₅+ R₇I₆.

Независимой проверкой является составление уравнения баланса мощностей (2.1) с учетом режимов работы элементов схемы с ЭДС:



Если активная мощность, поставляемая источниками питания, равна по величине активной мощности, израсходованной в пассивных элементах электрической цепи, то правильность расчетов подтверждена.
8. Основные методы расчета сложных электрических цепей

С помощью законов Ома и Кирхгофа в принципе можно рассчитать электрические цепи любой сложности. Однако решение в этом случае может оказаться слишком громоздким и потребует больших затрат времени. По этой причине для расчета сложных электрических цепей разработаны на основе законов Ома и Кирхгофа более рациональные методы расчета, два из которых: метод узлового напряжения и метод эквивалентного генератора, рассмотрены ниже.

2.8.1. Метод узлового напряжения

Этот метод рекомендуется использовать в том случае, если сложную электрическую схему можно упростить, заменяя последовательно и параллельно соединенные резисторы эквивалентными, используя при необходимости преобразование треугольника сопротивлений в эквивалентную звезду. Если полученная схема содержит несколько параллельно соединенных активных и пассивных ветвей, как, например, схема на рис. 2.27, то ее расчет и анализ весьма просто можно произвести методом узлового напряжения.

Пренебрегая сопротивлением проводов, соединяющих ветви цепи, в ее схеме (рис. 2.27) можно выделить два узла: a и b. В зависимости от значений и направлений ЭДС и напряжений, а также значений сопротивлений ветвей, между узловыми точками a и b установится определенное узловое напряжение U_ab. Предположим, что оно направлено так, как показано на рис. 2.27, и известно. Зная напряжение U_ab легко найти токи во всех ветвях. Выберем положительные направления токов и обозначим их на схеме. Запишем уравнения по второму закону Кирхгофа для контуров, проходящих по первой и второй ветви, содержащих источники ЭДС, совершая обход контуров по часовой стрелке.

Первая ветвь:

E₁ = (r₀₁ + R₁)∙I₁ + U_ab.

Вторая ветвь:

− E₂ = − (r₀₂ + R₂)∙I₂ + U_ab.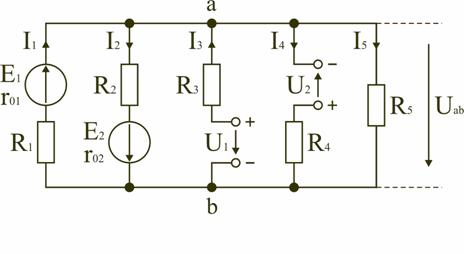

Рис. 2.27. Расчетная схема
Определим значения токов, возникающих в первой и второй ветвях,

	(2.6)
	(2.7)

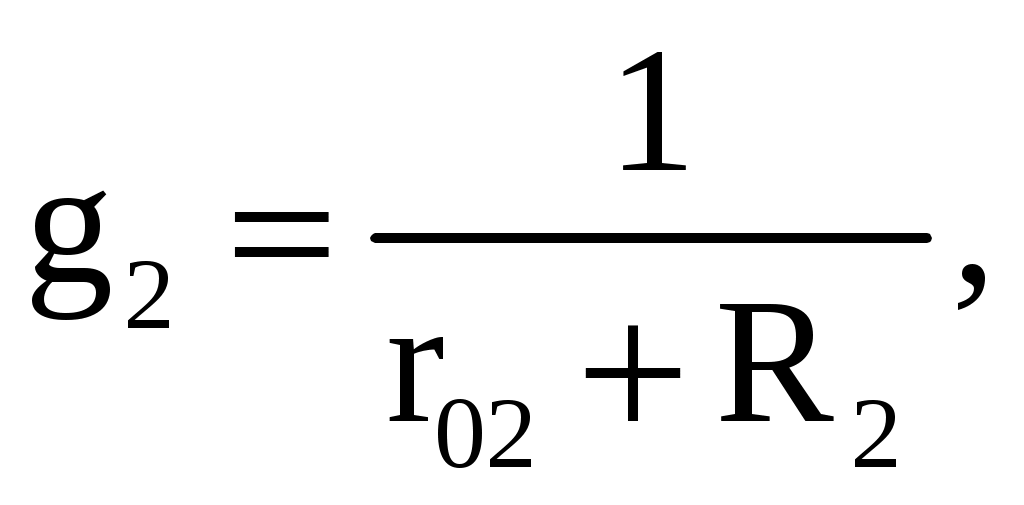где g_1, g₂ – проводимости соответственно первой и второй ветвей.

Запишем уравнения по второму закону Кирхгофа для ветвей, содержащих источники напряжений, совершая обход контуров также по часовой стрелке.
Третья ветвь: U_ab − U₁ + R₃I₃ = 0.

Четвертая ветвь: U_ab + U₂ − R₄I₄ = 0.

Определим значения токов, возникающих в третьей и четвертой ветвях,

	(2.8)
	(2.9)

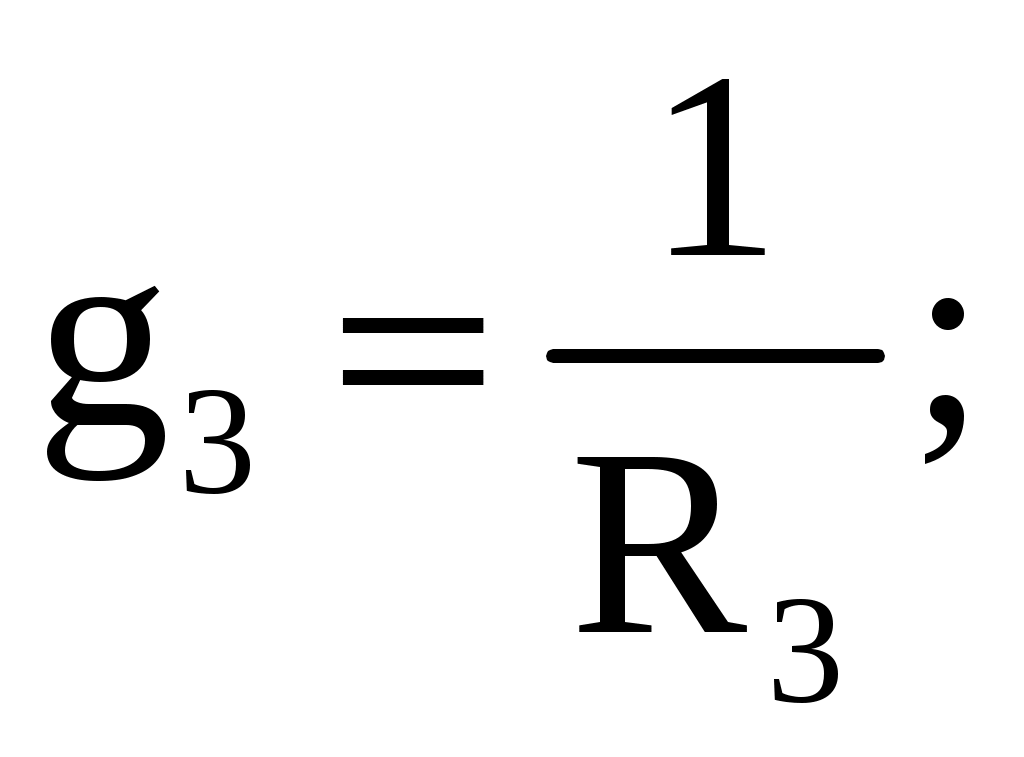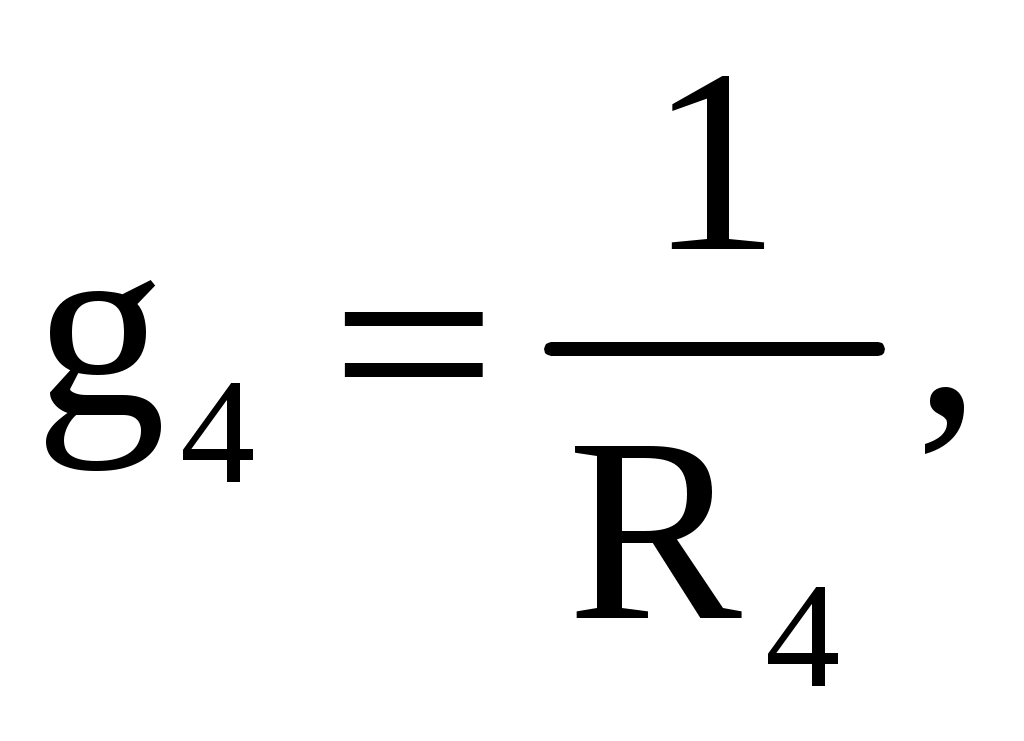где g_3, g₄ – проводимости соответственно третьей и четвертой ветвей.

Ток в пятой ветви определим по закону Ома:

(2.10)

где g₅ – проводимость пятой ветви.

Для вывода формулы, позволяющей определить напряжение U_ab, напишем уравнение по первому закону Кирхгофа для узла a:

I₁ − I₂ + I₃ − I₄ − I₅ = 0.

После замены токов их выражениями (2.6) – (2.10) и соответствующих преобразований получим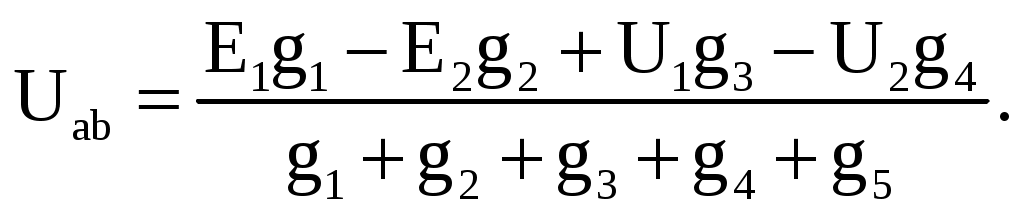



Формула узлового напряжения в общем случае имеет вид

(2.11)

При расчете электрической цепи методом узлового напряжения после определения величины напряжения U_ab значения токов в ветвях находят по их выражениям (2.6) – (2.10).

При записи формулы (2.11) следует задаться положительным направлением узлового напряжения U_ab. Со знаком «+» в (2.11) должны входить ЭДС, направленные между точками a и b встречно напряжению U_ab, и напряжения ветвей, направленные согласно с U_ab. Знаки в формуле (2.11) не зависят от направления токов ветвей.

При расчете и анализе электрических цепей методом узлового напряжения рекомендуется выбирать положительные направления токов после определения узлового напряжения. В этом случае при расчете токов по выражениям (2.6) – (2.11) положительные направления токов нетрудно выбрать таким образом, чтобы все они совпадали с их действительными направлениями.

Проверка правильности произведенных расчетов проводится по первому закону Кирхгофа для узла a или b, а также составлением уравнения баланса мощностей (2.1).
2.8.2. Метод эквивалентного генератора

Метод эквивалентного генератора позволяет произвести частичный анализ электрической цепи. Например, определить ток в какой-либо одной ветви сложной электрической цепи и исследовать поведение этой ветви при изменении ее сопротивления. Сущность метода заключается в том, что по отношению к исследуемой ветви amb (рис. 2.28 а) сложная цепь заменяется активным двухполюсником А (смотри рис. 2.23), схема замещения которого представляется эквивалентным источником (эквивалентным генератором) с ЭДС E_э и внутренним сопротивлением r_0э, нагрузкой для которого является сопротивление R ветви amb.

Если известны ЭДС и сопротивление эквивалентного генератора, то ток I в ветви amb определяется по закону Ома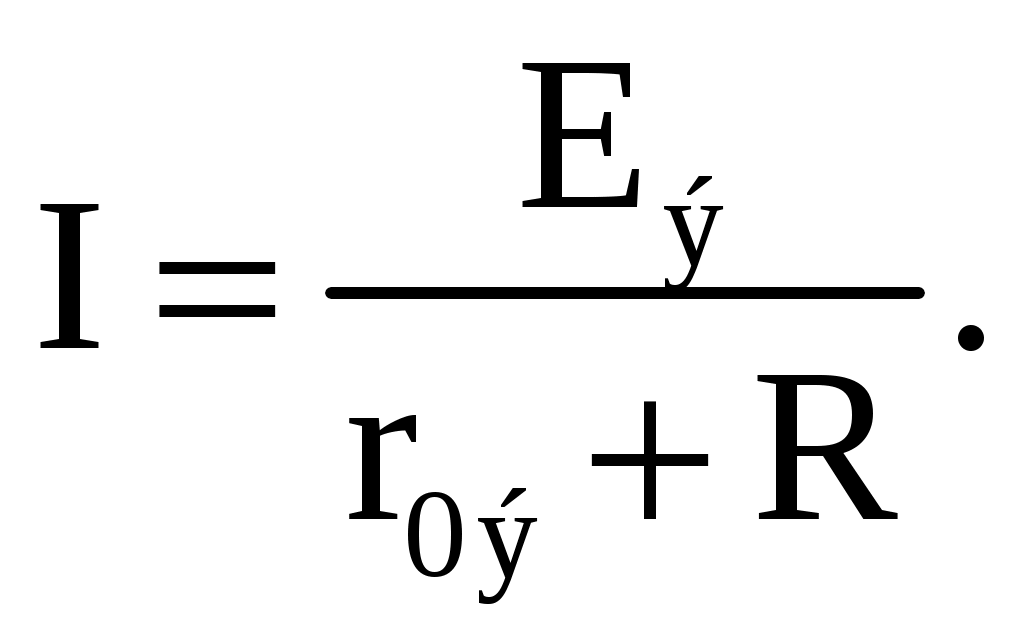



Покажем, что параметры эквивалентного генератора E_э и r_0э можно определить соответственно по режимам холостого хода и короткого замыкания активного двухполюсника.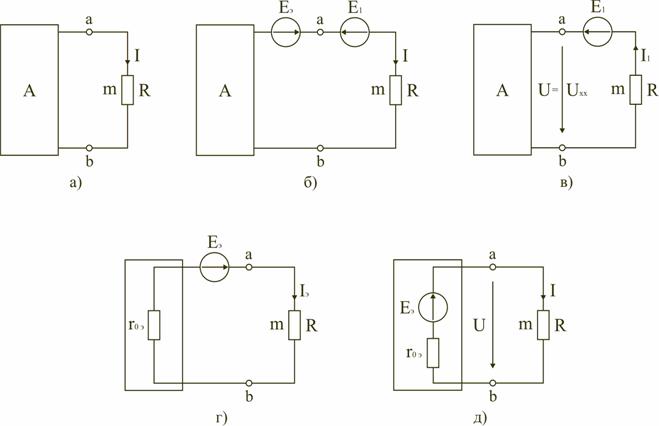

Рис. 2.28. Расчетные схемы
В исследуемую схему (рис. 2.28 а) введем два источника, ЭДС которых E₁ и E_э равны и направлены в разные стороны (рис. 2.28 б). При этом величина тока I в ветви amb не изменится. Ток I можно определить как разность двух токов I = I_э − I₁, где I₁ – ток, вызванный всеми источниками двухполюсника А и ЭДС E₁ (рис. 2.28 в); I_э – ток, вызванный только ЭДС E_э (рис. 2.28 г).

Если выбрать ЭДС E₁ такой величины, чтобы получить в схеме (2.28, в) ток I₁=0, то ток I будет равен (рис. 2.28 г)



где r_0э – эквивалентное сопротивление двухполюсника А относительно выводов а и b.

Так как при I₁ = 0 (рис. 2.28 в) активный двухполюсник А будет работать относительно ветви amb в режиме холостого хода, то между выводами a и b установится напряжение холостого хода U = U_хх и по второму закону Кирхгофа для контура amba получим E₁ = I₁R + U_хх = U_хх. Но по условию E_э = E₁, поэтому и E_э = U_хх. Учитывая это, формулу для определения тока I можно записать в такой форме: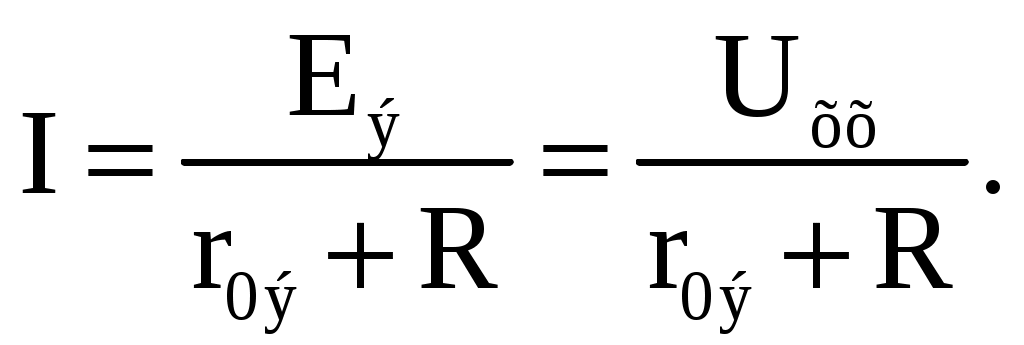



В соответствии с (2.8) электрическая цепь на рис. 2.28 а может быть заменена эквивалентной цепью (рис. 2.28 д), в которой E_э = U_хх и r_0э следует рассматривать в качестве параметров некоторого эквивалентного генератора.

Значения E_э = U_хх и r_0э можно определить как расчетным, так и экспериментальным путем. Для расчетного определения U_хх и r_0э необходимо знать параметры элементов активного двухполюсника и схему их соединения.

Для определения величины r_0э необходимо удалить из схемы двухполюсника все источники, сохранив все резистивные элементы, в том числе и внутренние сопротивления источников ЭДС. Внутренние сопротивления источников напряжений принять равными нулю. Затем рассчитать известными методами эквивалентное сопротивление относительно выводов ab.

Для определения величины E_э разомкнем цепь и определим по методу узлового напряжения напряжение U_ab = U_хх = E_э между выводами ab активного двухполюсника.

Экспериментально параметры эквивалентного генератора можно определить по результатам двух опытов. Разомкнув ветвь с сопротивление R (рис. 2.28 д), измеряем напряжение между выводами a и b U_ab = U_хх = E_э (опыт холостого хода).

Для определения r_0э проводится (если это допустимо) опыт короткого замыкания: заданная ветвь замыкается накоротко и в ней измеряется ток короткого замыкания I_кз. По закону Ома рассчитываем величину r_0э = E_э/I_кз.