Электротехника
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
ЛАБОРАТОРНАЯ РАБОТА №3«ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКАС ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ЭЛЕМЕНТОВ»Цель работы Изучение свойств цепей переменного тока при последовательном соединении активных и реактивных элементов, знакомство с явлением резонанса напряжений, построение векторных диаграмм. Пояснения к работе При расчете цепей переменного тока, в отличие от цепей постоянного тока, необходимо учитывать не один, а три простейших пассивных элемента: резистивный, индуктивный и емкостной. В реальной цепи активным сопротивлением R обладают не только резистор или реостат как устройства, предназначенные для использования их электрических сопротивлений, но и любой проводник, катушка, конденсатор, обмотка любого электромагнитного элемента и др. Общим свойством всех устройств, обладающих активным электрическим сопротивлением, является необратимое преобразование электрической энергии в тепловую энергию. Напряжение, подведенное к активному сопротивлению, по фазе совпадает с током, то есть напряжение и ток одновременно достигают максимальных значений и одновременно переходят через нуль. Индуктивность L характеризует свойство участка цепи или катушки накапливать энергию магнитного поля. В реальной цепи индуктивностью обладают не только индуктивные катушки, но и провода, и выводы конденсаторов, и реостаты. Индуктивность в цепи переменного тока влияет на величину протекающего тока как сопротивление. Соответствующая расчетная величина называется реактивным индуктивным сопротивлением ХLи измеряется так же, как и активное сопротивление – в Омах. 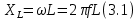 Величина 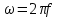 называется угловой (циклической) частотой переменного тока. Чем выше частота переменного тока, тем больше индуктивное сопротивление. называется угловой (циклической) частотой переменного тока. Чем выше частота переменного тока, тем больше индуктивное сопротивление. На участке цепи с индуктивностью напряжение, опережает ток на 90о или на 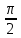 радиана. При включении в цепь переменного тока реальной катушки (рис. 3.1), обладающей кроме индуктивности Lи некоторым значением активного сопротивления RK, ток отстает по фазе от напряжения на некоторый угол радиана. При включении в цепь переменного тока реальной катушки (рис. 3.1), обладающей кроме индуктивности Lи некоторым значением активного сопротивления RK, ток отстает по фазе от напряжения на некоторый угол 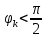 , который легко определяется из треугольника сопротивлений (рис. 3.3): , который легко определяется из треугольника сопротивлений (рис. 3.3):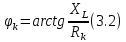 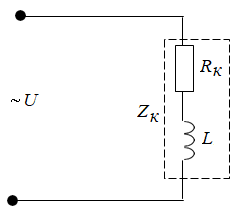 Рис. 3.1 Схема замещения реальной катушки индуктивности В напряжении 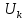 , подведенном к реальной катушке, условно можно выделить две составляющих: падение напряжения , подведенном к реальной катушке, условно можно выделить две составляющих: падение напряжения 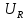 на активном сопротивлении, обычно называемое активной составляющей, и напряжение на идеальной индуктивности на активном сопротивлении, обычно называемое активной составляющей, и напряжение на идеальной индуктивности 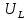 , называемое реактивной составляющей приложенного напряжения. Фазовые соотношения между этими составляющими и приложенным напряжением иллюстрируются векторной диаграммой для их действующих значений (рис. 3.2). , называемое реактивной составляющей приложенного напряжения. Фазовые соотношения между этими составляющими и приложенным напряжением иллюстрируются векторной диаграммой для их действующих значений (рис. 3.2).  Рис. 3.2 Векторная диаграмма напряжений катушки индуктивности Из векторной диаграммы видно, что  где  - полное электрическое сопротивление реальной катушки. - полное электрическое сопротивление реальной катушки. Закон Ома для катушки, по которой протекает переменный ток, записывается в виде: 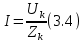 Из треугольника сопротивлений (рис. 3.3) также следуют соотношения: 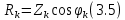 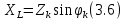 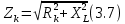 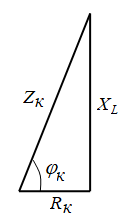 Рис. 3.3 Треугольник сопротивлений реальной катушки индуктивности Из рассмотренного следует важный вывод: сопротивления в цепи переменного тока складываются в общем случае геометрически. Например, если у катушки Rk=3 Ома и ХL = 4 Ома, то полное сопротивление Zк= 5 Ом. Емкость характеризует способность элемента электрической цепи или конденсатора накапливать энергию электрического поля. В реальной цепи емкость существует не только в конденсаторах, но и между проводниками, между витками катушек (межвитковая емкость), между проводом и землей или каркасом электротехнического устройства. Влияние емкости С на величину протекающего в цепи тока характеризуют реактивным емкостным сопротивлением ХС,котороеизмеряется в Омах и является обратно пропорциональной функцией частоты. 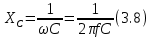 Напряжение на емкости отстает от тока по фазе на 90о или 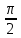 радиан. Векторная диаграмма тока и напряжения для участка электрической цепи, содержащей емкость, изображена на рисунке.3.4. радиан. Векторная диаграмма тока и напряжения для участка электрической цепи, содержащей емкость, изображена на рисунке.3.4.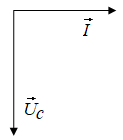 Рис. 3.4 Векторная диаграмма для участка цепи с емкостью. В электрических цепях переменного тока используют понятия активной, реактивной и полной мощности. Активная мощность 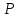 выделяется на резистивных элементах, измеряется в ваттах (Вт). Равна произведению действующего значения напряжения выделяется на резистивных элементах, измеряется в ваттах (Вт). Равна произведению действующего значения напряжения 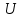 на действующее значение тока на действующее значение тока 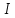 и на и на 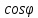 , называемый коэффициентом мощности, или произведению квадрата действующего значения тока на активное сопротивление: , называемый коэффициентом мощности, или произведению квадрата действующего значения тока на активное сопротивление: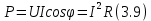 Реактивная мощность 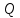 характеризует изменение энергии в реактивных элементах - индуктивностях и емкостях, измеряется в вольт-амперах реактивных (ВАр). Равна произведению действующего значения напряжения характеризует изменение энергии в реактивных элементах - индуктивностях и емкостях, измеряется в вольт-амперах реактивных (ВАр). Равна произведению действующего значения напряжения 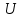 на действующее значение тока на действующее значение тока 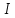 и на и на 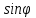 или произведению квадрата действующего значения тока на реактивное сопротивление. или произведению квадрата действующего значения тока на реактивное сопротивление.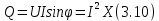 Различают реактивную индуктивную мощность QL и реактивную емкостную мощность QC. 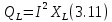 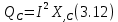 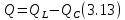 Полная мощность 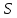 , измеряемая в вольт-амперах (ВА), равна произведению действующего значения тока , измеряемая в вольт-амперах (ВА), равна произведению действующего значения тока 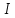 на действующее значение напряжения на действующее значение напряжения 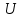 : : 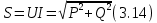 Соотношения этих мощностей иллюстрируются треугольником мощностей (рис. 3.5).  Рис. 3.5 Треугольник мощностей Электрическая цепь синусоидального переменного тока с последовательным соединением резистора с активным сопротивлением 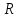 , реальной катушки индуктивности с полным сопротивлением , реальной катушки индуктивности с полным сопротивлением 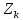 и конденсатора с емкостным сопротивлением и конденсатора с емкостным сопротивлением 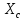 (рис. 3.6а) описывается уравнением, записанным по второму закону Кирхгофа для мгновенных значений напряжений на этих элементах: (рис. 3.6а) описывается уравнением, записанным по второму закону Кирхгофа для мгновенных значений напряжений на этих элементах: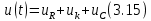 или в геометрической форме для векторов действующих значений этих напряжений: 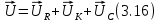 Последнее соотношение говорит о том, что вектор действующего значения напряжения, приложенного к такой цепи, равен геометрической сумме векторов напряжений на отдельных её участках (рис. 4.6б). 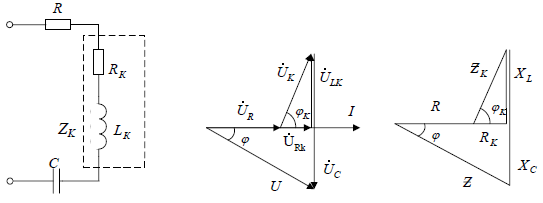 а б в Рис. 3.6 Последовательное соединением резистора, катушки индуктивности и конденсатора Из анализа векторной диаграммы для такой цепи следует, что величина входного напряжения 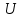 : :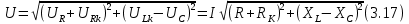 где 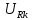 , , 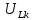 – соответственно активная и реактивная составляющие напряжения на катушке, – соответственно активная и реактивная составляющие напряжения на катушке, 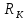 , , 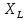 – активное и реактивное индуктивное сопротивление катушки индуктивности. – активное и реактивное индуктивное сопротивление катушки индуктивности.Следовательно, действующее значение тока в этой цепи на основании закона Ома можно определить, как 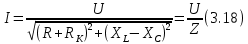 где 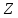 - полное сопротивление цепи с последовательным соединением резистора, катушки индуктивности и конденсатора, которое легко определяется из треугольника сопротивлений (рис. 4.6в): - полное сопротивление цепи с последовательным соединением резистора, катушки индуктивности и конденсатора, которое легко определяется из треугольника сопротивлений (рис. 4.6в):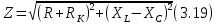 Угол сдвига фаз 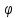 между входным синусоидальным напряжением между входным синусоидальным напряжением 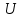 и потребляемым цепью током и потребляемым цепью током 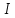 определяется из треугольника сопротивлений: определяется из треугольника сопротивлений: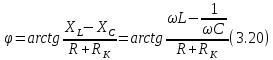 Если индуктивное сопротивление в цепи больше емкостного сопротивления ( 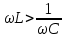 ), тоугол ), тоугол 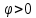 , вся цепь ведет себя как цепь с активным сопротивлением и идеальной индуктивностью. Говорят, что в этом случае цепь носит активно-индуктивный характер. , вся цепь ведет себя как цепь с активным сопротивлением и идеальной индуктивностью. Говорят, что в этом случае цепь носит активно-индуктивный характер.Если индуктивное сопротивление в цепи меньше емкостного сопротивления ( 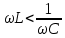 ), то угол ), то угол 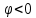 , вся цепь ведет себя как цепь с активным сопротивлением и емкостью. Говорят, что в этом случае цепь носит активно-емкостной характер. , вся цепь ведет себя как цепь с активным сопротивлением и емкостью. Говорят, что в этом случае цепь носит активно-емкостной характер.Если в цепи реактивные сопротивления равны ( 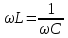 ), то угол ), то угол 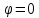 . При этом реактивная составляющая напряжения на индуктивности и напряжение на конденсаторе полностью компенсируют друг друга. Цепь ведет себя, как будто реактивные сопротивления в ней отсутствуют и ток достигает наибольшего значения, поскольку ток ограничивается только эквивалентным активным сопротивлением цепи . При этом реактивная составляющая напряжения на индуктивности и напряжение на конденсаторе полностью компенсируют друг друга. Цепь ведет себя, как будто реактивные сопротивления в ней отсутствуют и ток достигает наибольшего значения, поскольку ток ограничивается только эквивалентным активным сопротивлением цепи 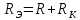 . . Это означает, что в цепи имеет место резонанс, называемый в данном случае резонансом напряжений. Резонанс напряжений можно получить либо изменением частоты источника питания, либо подбором значения величины емкости конденсатора: Это означает, что в цепи имеет место резонанс, называемый в данном случае резонансом напряжений. Резонанс напряжений можно получить либо изменением частоты источника питания, либо подбором значения величины емкости конденсатора: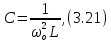 где 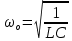 - резонансная частота цепи. - резонансная частота цепи.Порядок выполнения работы Ознакомиться с лабораторной установкой (модуль питания, измеритель мощности, модуль резисторов, модуль реактивных элементов). В соответствии со схемой установки на рисунке 3.7 нарисовать электрическую схему исследуемой цепи. 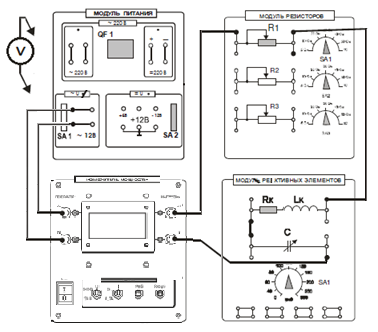 Рис. 4.7 Схема лабораторного стенда Собрать электрическую цепь (рис. 3.7), установив значения сопротивления резистора 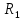 и емкости конденсатора и емкости конденсатора 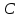 в соответствии с вариантом (табл. 3.1). Подсоединить параллельно конденсатору дополнительный проводник (исключив этим конденсатор из цепи). Предъявить схему для проверки преподавателю. в соответствии с вариантом (табл. 3.1). Подсоединить параллельно конденсатору дополнительный проводник (исключив этим конденсатор из цепи). Предъявить схему для проверки преподавателю.Таблица 3.1 Значения сопротивления резистора и емкости
Включить электропитание стенда (выключатель QF и SA1 модуля питания). Произвести измерения указанных в таблице 3.2 величин в цепи с последовательным соединением резистора R и индуктивной катушки ZK. Выключить источник переменного напряжения (SA1). Таблица 3.2 Результаты измерений
Удалить проводник, включенный параллельно конденсатору. Подсоединить дополнительный проводник параллельно индуктивной катушке (исключив этим вместо конденсатора индуктивную катушку из цепи). Предъявить схему для проверки преподавателю. Включить источник электропитания и произвести измерения указанных в таблице 3.2 величин для цепи с последовательным соединением резистора R и конденсатора С. Выключить электропитание, убрать дополнительный проводник. В цепи с последовательным соединением резистора R, индуктивной катушки ZK и конденсатора C, изменяя величину емкости конденсатора с помощью переключателя SA1 модуля реактивных элементов, добиться наименьшего угла сдвига фаз, т.е. обеспечить состояние цепи близкое к резонансу напряжений. Результаты измерений занести в таблицу 3.2. Уменьшая до наименьшего и увеличивая до наибольшего значения величину емкости конденсатора C (от резонансного значения) провести измерения указанных в таблице величин для двух состояний цепи. Результаты измерений занести в таблицу 3.2. Выключить электропитание стенда. Для цепи с последовательным соединением трех элементов (R,ZK, С) по результатам измерений рассчитать величины, указанные в таблицу 3.3. Таблица 3.3 Рассчетные величины
По результатам измерений построить для исследованных цепей в масштабе векторные диаграммы. Содержание отчета Отчет по работе должен содержать: Титульный лист. Цель работы. Схему исследуемой цепи. Таблицы с результатами измерений и вычислений. Расчетные соотношения.; Векторные диаграммы. Выводы по работе. Контрольные вопросы Что такое активная, реактивная и полная мощности в цепи переменного тока? Какая взаимосвязьмежду полной, активной и реактивной мощностями? Что такое «коэффициент мощности»? Как вычислить полное сопротивление катушки, если известны её активное сопротивление, индуктивность и частота сети? Как вычислить полное сопротивление цепи с последовательным соединением резистора, реальной катушки и конденсатора? От чего зависит угол сдвига фаз между напряжением и током на участке электрической цепи переменного тока? Что такое «треугольник сопротивлений»? Чему равны реактивное сопротивление цепи и реактивная мощность цепи при резонансе? Каков при этом характер цепи? |
