ЛР 1-2 Послед. и пар. соединение 05.09. ЛР 1-2 Послед. и пар. соединение 05. Исследование однофазных цепей переменного тока методические указания к лабораторным работам СанктПетербург 1994
 Скачать 3.3 Mb.
|
1 2 МИНИСТЕРСТВО ПУТЕЙ СООБЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ Кафедра «Электротехника» ИССЛЕДОВАНИЕ ОДНОФАЗНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА Методические указания к лабораторным работам Санкт-Петербург 1994 КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ Однофазная электрическая цепь – это цепь переменного тока, состоящая из приёмников электрической энергии, получающих питание от однофазного генератора синусоидальной ЭДС. В качестве приемников электрической энергия в цепь переменного тока могут быть включены резистивный элемент (активное сопротивление  ) и реактивные элементы: катушка индуктивности и конденсатор, характеризуемые соответственно параметрами Lи С.Возможны две схемы включения этих приемников: 1) последовательное соединение активного сопротивления r, индуктивности L и емкости С (рис. 1); 2) параллельное соединение активного сопротивления , индуктивности L и емкости С (рис. 2).
В цепи последовательного соединения , L, C (рис. 1) все приемники характеризуются одним и тем же синусоидальным током ,который протекает под действием синусоидального напряжения, приложенного к цепи  ,где  – соответственно мгновенные значения тока и напряжения; – cответственно амплитудные значения тока и напряжения; – угловая частота ( – частота);  – время;φ - сдвиг фаз между напряжением и током. Измерительные приборы (амперметр, вольтметр) регистрируют так называемые действующие значения переменного тока  и напряжения  : ,  .Расчеты электрических цепей, как правило, ведутся для действующих значений тока и напряжения. Ток в цепи последовательного соединения , L, C (см. рис. 1) создает на каждом из участков этой цепи падения напряжения, равные произведению тока на сопротивление участка. Напряжение на активном сопротивлении  совпадает по фазе с током (рис. 3,а). Напряжение на индуктивности  опережает по фазе ток на угол  , причем коэффициент пропорциональности между индуктивным напряжением и током  называется индуктивным сопротивлением. Напряжение на емкости  отстает по фазе от тока на угол и равно  , где  – емкостное сопротивление.Вектор действующего значения напряжения на входных зажимах согласно второму закону Кирхгофа равен геометрической сумме действующих значений напряжений на отдельных участках цепи т.е.  . (1)Поэтому на векторной диаграмме напряжений и токов (рис.3,а), представляющей собой графическое решение уравнения (1), вектор полного напряжения замык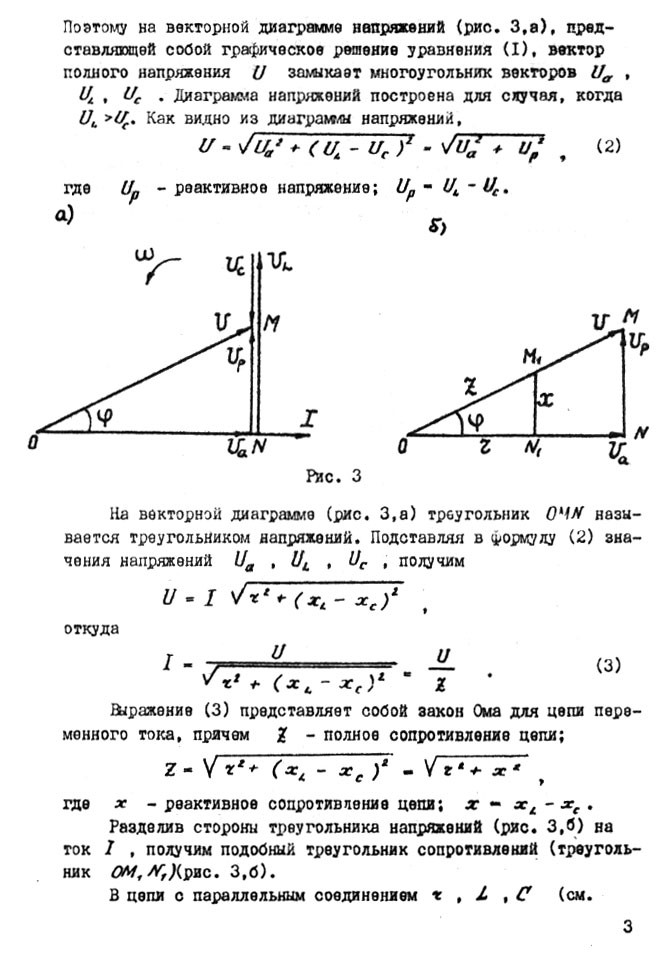ает многоугольник векторов  ,  , . Диаграмма напряжений построена для случая, когда  . Как видно из диаграммы напряжений, , (2)где  – реактивное напряжение;  . а) б)  Рис. 3 На векторной диаграмме (рис. 3,а) треугольник OMNназывается треугольником напряжений. Подставляя в формулу (2) значения напряжений  , ,  , получим ,откуда  . (3)Выражение (3) представляет собой закон Ома для последовательной цепи переменного тока, причем  – полное сопротивление цепи; ,где  – реактивное сопротивление цепи;  .Разделив стороны треугольника напряжений (рис. 3,а) на ток , получим подобный треугольник сопротивлений (треугольник OM1N1 (рис. 3,б)).В цепи с параллельным соединением , L, C (см. рис. 2) все приемники находятся под одним и тем же напряжением питающей сети . Согласно первому закону Кирхгофа для действующих значений, вектор тока в неразветвлённой части цепи равен геометрической сумме токов параллельных ветвей: . (4)По уравнению (4) на рис. 4,а построена векторная диаграмма токов. Активный ток  совпадает по фазе с напряжением и определяется по формуле  , где  – активная проводимость.Индуктивный ток  отстает по фазе от напряжения на угол ;  , где  – индуктивная проводимость. Емкостной ток  опережает по фазе напряжение на угол ;  , где  – ёмкостная проводимость.Как видно из диаграммы токов (рис. 4,а), полный ток  ,где  – реактивный ток;  .а) б)  Рис. 4 Векторную диаграмму токов (рис. 4,б) называют треугольником токов (треугольник ОМN). Разделив стороны треугольника токов на напряжение U, подучим треугольник проводимостей OM1N1, сторонами которого будут:  – активная проводимость;  – реактивная проводимость;  – полная проводимость.Лабораторная работа №1 Последовательной соединение резистора, катушки индуктивности и конденсатора. Резонанс напряжений. Цель работы – изучение основных соотношений в однофазной цепи переменного тока при последовательном соединении приемников, а также исследование явления резонанса напряжений. При исследовании последовательной цепи переменного тока между собой соединяются три приемника электрической энергии: резистор (проволочный или ламповый реостат), катушка индуктивности со стальным сердечником и батарея конденсаторов (рис. 5). 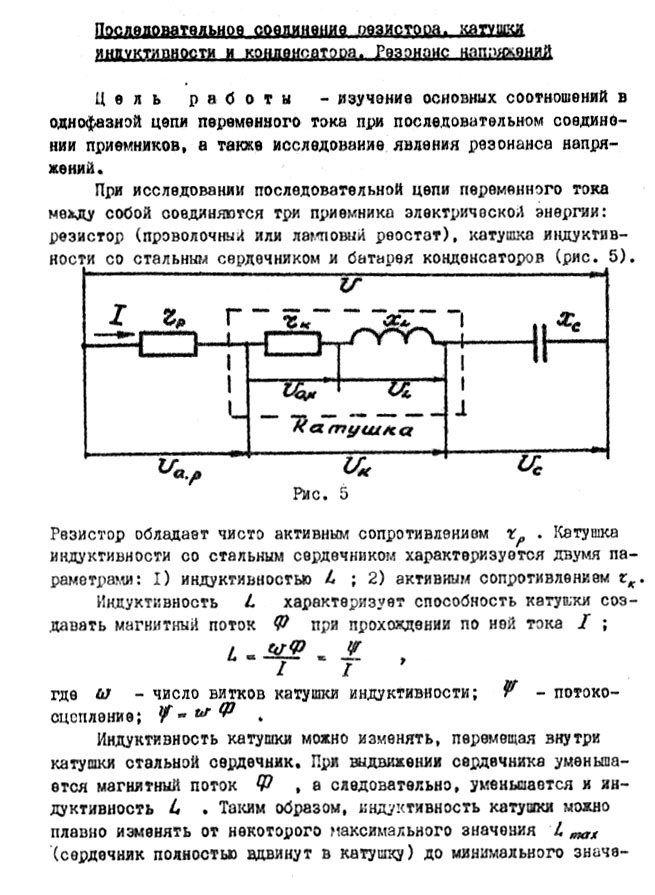 Рис. 5 Резистор обладает чисто активным сопротивлением  . Катушка индуктивности со стальным сердечником характеризуется двумя параметрами: 1) индуктивностью  ; 2) активным сопротивлением  . Индуктивность характеризует способность катушки создавать магнитный поток Ф при прохождении по ней тока ; ,где  – число витков катушки индуктивности;  – потокосцепление;  .Индуктивность катушки можно изменять, перемещая внутри катушки стальной сердечник. При выдвижении сердечника уменьшается магнитный поток  , а следовательно, уменьшается и индуктивность . Таким образом, индуктивность катушки можно плавно изменять от некоторого максимального значения  (сердечник полностью вдвинут в катушку) до минимального значения  (сердечник выдвинут из катушки).Активное сопротивление катушки обусловлено наличием сопротивления провода её обмотки, а также потерь энергии в стальном сердечнике (на гистерезис и вихревые токи). Часто при рассмотрении теоретических вопросов принимают  . В этом случае катушку индуктивности называют идеальной.Реальная катушка индуктивности характеризуется двумя сопротивлениями: 1) индуктивным ; 2) активным .Батарея конденсаторов емкостью С характеризуется емкостным сопротивлением  . Активным сопротивлением конденсатора, эквивалентным потерям энергии в диэлектрике от токов утечки, в дальнейшем будем пренебрегать ввиду малой величины.Последовательное соединение резистора, катушки индуктивности и батареи конденсаторов может быть представлено эквивалентной схемой, изображенной на рис. 5, где указаны действующие значения напряжений:  – напряжение на резисторе;  – напряжение на катушке индуктивности; – напряжение на конденсаторе; – полное напряжение на входе цепи.Напряжение на катушке  можно условно представить двумя составляющими:  – активным напряжением катушки; – индуктивным напряжением катушки.Является очевидным, что  (геометрическая сумма). Практически вольтметром можно измерить только , а напряжение  и – нельзя. Полное напряжение всей цепи согласно второму закону Кирхгофа равно геометрической сумме напряжений на отдельных участках цепи, т.е.  . Согласно этому уравнению, на рис. 6 построена векторная диаграмма напряжений, когда  ().  Рис. 6 В этом случае говорят, что в цепи преобладает индуктивная нагрузка. При построении векторной диаграммы вначале проводят вектор тока . Векторы напряжений строят в таком порядке: вначале проводят вектор  , который совпадает по фазе c вектором тока  . Из конца вектора под углом  (значение угла определяется расчетом) проводят вектор  , из конца вектора проводят вектор  под углом к вектору тока . Вектор является замыкающим вектором многоугольника напряжений. Построение векторной диаграммы напряжений можно выполнить и вторым способом – с помощью циркуля методом «засечек» (рис. 7). Этот способ удобен тогда, когда неизвестен угол . В этом случае из конца вектора проводят перпендикулярно вектору тока вектор и далее циркулем делает две «засечки»: одну – из точки О радиусом , другую – из конца вектора радиусом . Затем вектор раскладывают на две составляющие (см. рис. 6): вектор  , совпадающий с током , и вектор , опережающий ток на угол .Если разделить все векторы напряжений (см. рис. 6) на ток , получится подобный многоугольник сопротивлений (рис. 8). Из рассмотрения многоугольников напряжений (см. рис. 6) и сопротивлений (рис. 8) можно сформулировать основные правила сложения напряжений и сопротивлений в цепи переменного тока при последовательном соединении приемников электрической энергии:
1) активные напряжения и сопротивления складываются арифметически, т.е.  ; ;2) реактивные напряжения и сопротивления складываются алгебраически, т.е.  ; ,при этом индуктивные величины входят в суммы с положительным знаком, емкостные – с отрицательным; 3) полные напряжения и сопротивления получаются посредством геометрического сложения активных и реактивных составляющих, т.е.  или  и аналогично полное сопротивление цепи  .Как известно, геометрическое сложение векторов можно заменить алгебраическим сложением комплексных чисел, изображающих эти векторы. Таким образом, используя символический метод расчета цепей переменного тока (метод комплексных чисел), можно записать  ,где  ,  ,  – комплексные напряжения.Аналогично  ,где  – комплексное сопротивление;  – мнимая единица;  .При изменении индуктивности за счет перемещения стального сердечника внутри катушки в цепи последовательного соединения можно добиться трех режимов:1) при цепь имеет активно-индуктивный характер. В этом случае ток в цепи отстает по фазе от напряжения на угол  (см. рис. 6);2) при  цепь имеет активно-емкостной характер и ток в цепи будет опережать напряжение на угол (рис. 9);3) при равенства индуктивного и емкостного сопротивлений  в цепи наступает резонанс напряжений (рис. 10).
Явление резонанса напряжений характеризуется следующими признаками. 1. При резонансе напряжений  и равны между собой по величине и противоположны по знаку:  , причем при малой активном сопротивлении цепи ( и  ) напряжения и могут значительно превышать напряжение сети . В этом заключается отрицательная сторона явления резонанса напряжений, так как возникновение перенапряжений может привести к пробою изоляции и оказаться опасным для персонала.2. При резонансе напряжений ток в цепи достигает максимального значения  (рис. 11), что вытекает из формулы ,которая при 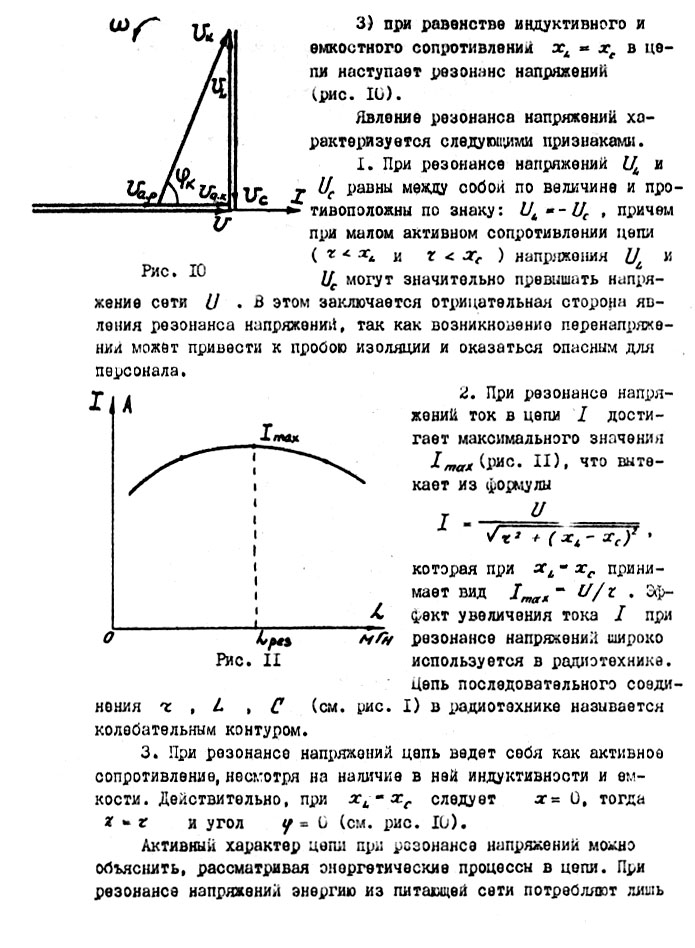принимает вид  . Эффект увеличения тока при резонансе напряжений широко используется в радиотехнике. Цепь последовательного соединения , L,C (см. рис. 11) в радиотехнике называется колебательным контуром. Рис. 11 3. При резонансе напряжений цепь ведет себя как активное сопротивление, несмотря на наличие в ней индуктивности и емкости. Действительно, при следует  , тогда  и угол  (см. рис. 10).Активный характер цепи при резонансе напряжений можно объяснить, рассматривая энергетические процессы в цепи. При резонансе напряжений энергию из питающей сети потребляют лишь активные сопротивления резистора и катушки, а индуктивность и емкость взаимно обмениваются энергией и из сети ее не потребляют. 4. Пря резонансе напряжений частота источника питания f равна собственной частоте колебании контура  , т.е.  . Собственная частота контура определяется из условия резонанса напряжений . Так как  , а  , то  , отсюда  .При постоянной частоте источника питания f=50Гц равенства . т.е. резонанса напряжений, можно добиться тремя способами:изменением индуктивности L; изменением емкости С или совместным изменением L и С . Программа работы Исследовать работу схемы при изменении индуктивности катушки и неизменных значениях сопротивления резистора и емкости: 1) до резонанса напряжений; 2) при резонансе напряжений; 3) после резонанса напряжений. Схема соединений Схема с последовательным соединением резистора, катушки индуктивности и конденсатора показана на рис. 12. Здесь обозначены: 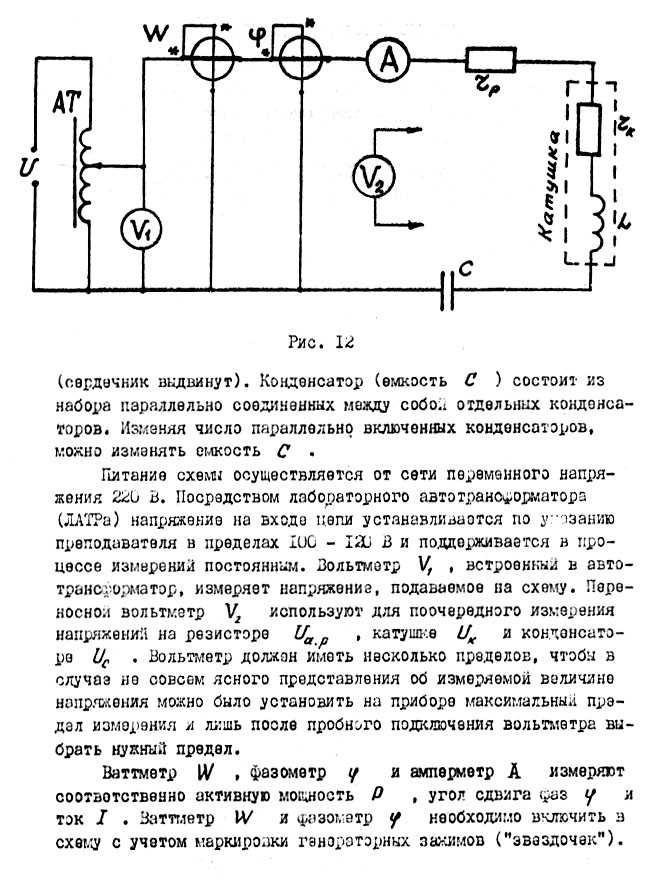 – сопротивление резистора;  и L – соответственно активное сопротивление катушки и ее индуктивность; С– емкость конденсатора. Рис. 12 Резистором является проволочный (или ламповый) реостат. Катушка индуктивности имеет ферромагнитный сердечник, перемещением которого можно изменять индуктивность катушки L от максимального значения (сердечник вдвинут) до минимального (сердечник выдвинут). Конденсатор (емкость С) состоит из набора параллельно соединенных между собой отдельных конденсаторов. Изменяя число параллельно включенных конденсаторов, можно изменять емкость С. Питание схемы осуществляется от сети переменного напряжения 220В. Посредством лабораторного автотрансформатора (ЛАТРа) напряжение на входе цепи устанавливается по указанию преподавателя в пределах 100-120В и поддерживается в процессе измерений постоянным. Вольтметр V1, встроенный в автотрансформатор, измеряет напряжение, подаваемое на схему. Переносной вольтметр V2 используют для поочередного измерения напряжения на резисторе , катушке  иконденсаторе  . Вольтметр должен иметь несколько пределов, чтобы в случае не совсем ясного представления об значении измеряемого напряжения можно было установить на приборе максимальный предел измерения и лишь после пробного подключения вольтметра выбрать нужный предел.Ваттметр W фазометр φ и амперметр А измеряют соответственно активную мощность Р, угол сдвига фаз φ и ток . Ваттметр W и фазометр φ необходимо включить в схему с учетом маркировки генераторных зажимов («звёздочек»).Порядок выполнения работы 1. Ознакомиться с приборами и оборудованием экспериментальной установки. Записать данные приборов в табл. 1. в которой в качестве примера приведены характеристики ваттметра. Таблица 1
ПРИМЕЧАНИЯ: 1. Если прибор многопредельный, записывают тот предел измерения, на который прибор был включен. 2. Предел измерения ваттметра определяется как произведение пределов измерения токовой обмотки и обмотки напряжения. Например, токовая обмотка включена на 5 А, обмотка напряжения – на 150 В, тогда предел измерения ваттметра равен: 5 А х 150 В =150 Вт. Цена деления прибора определяется как частное от деления предела измерения прибора на число делений школы. В частности, если шкала имеет 150 делении, то цена деления ваттметра равна 750 Вт: 150 дел =5 Вт/дел. 2. Собрать схему согласно рис. 12. Сборку схемы рекомендуется начать от выходных зажимов автотрансформатора. Вначале собирается последовательная часть электрической цепи. У фазометра и ваттметра сначала включаются токовые зажимы. Вольтметровые обмотки этих приборов включаются параллельно нагрузке (приемнику) после сборки последовательной цепи. 3. Перед включением установки в сеть установить ручку лабораторного автотрансформатора в положение, обеспечивающее нулевое напряжение на его выходных зажимах. 4. После включения установки в сеть плавно повышать автотрансформатором напряжение до заданного значения (порядка 100 – 120 В) и далее поддерживать постоянным. 5. В начале исследования сердечник должен быть вдвинут в катушку. Затем, плавно выдвигая сердечник из катушки, необходимо выполнить, пять измерений: два – до наступления явления резонанса напряжений, одно – при резонансе напряжений и два последних – после резонанса. Состояние резонанса точнее всего определяется по фазометру: при резонансе угол φ = 0. Переносной вольтметр V2 служит для измерения напряжений на отдельных участках цепи: на резисторе , катушке и конденсаторе . Результаты измерений записываются в табл. 2.Содержание отчета 1. Цель работы и программа. 2. Схема соединений (рис. 12). 3. Таблица данных электроизмерительных приборов (табл. 1). 4. Таблица наблюдений и вычислений (табл. 2). 5. Примеры вычислений. 6. Три векторные диаграммы напряжений для первой, третьей и пятой строк табл. 2. Векторные диаграммы строятся на миллиметровой бумаге в одном масштабе (1 см – 10 В) для всех трех случаев. 7. Треугольники сопротивления , , для всех трех случаев, что и в п. 6.8. Кривая тока  .9. Выводы по работе (ответы на вопросы). Таблица 2
Формулы для выполнения расчётов имеют вид
Расчет производятся для всех пяти строк таблицы. Пример расчета приводится только для одной строки по указанию преподавателя. основные вопросы по работе 1. Как складываются действующие значения напряжений и сопротивления в последовательной цепи переменного тока? 2. При каких условиях возникает резонанс напряжений и каковы характерные признаки резонансного состояния? 3. В чём заключается практическое использование резонанса напряжений? 4. Чем опасно явление резонанса напряжений? Лабораторная работа №2 1 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.
.
или
и 
определяются соответственно по пп. 7 и 8. Эта формула позволяет определить знак у реактивного сопротивления (плюс или минус).
.
.
.
.
.
, где 
, 
50 Гц.
.
.