|
|
Контрольная работа. 1-Кинематика. Элементы кинематики
1. ЭЛЕМЕНТЫ КИНЕМАТИКИ
1.1. Основные понятия и уравнения
Первая часть курса физики «Физические основы механики» изучает закономерности механического движения, которое представляет собой простейший вид движения, состоящий в изменении положения тел или их частей относительно друг друга. Кинематика как раздел механики изучает закономерности механического движения без выяснения причины этого движения.
Кинематика поступательного движения
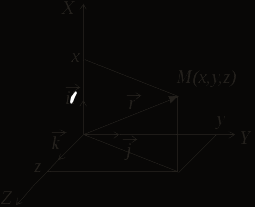
В ортогональной системе координат положение материальной точки или частицы (в дальнейшем – частицы) в пространстве в зависимости от времени 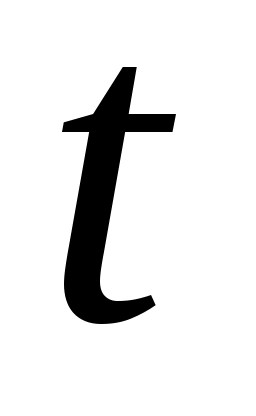 определяет векторное уравнение радиус-вектора определяет векторное уравнение радиус-вектора 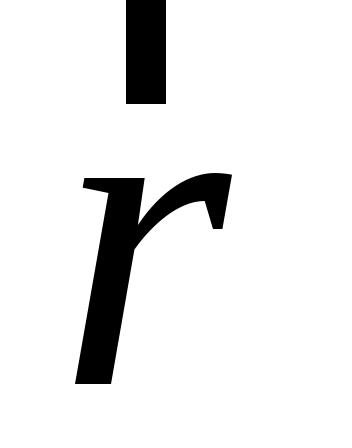 вида: вида:
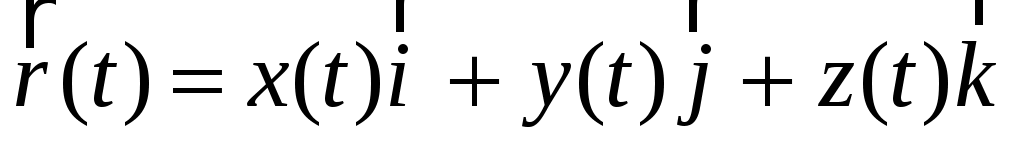 , (1.1) , (1.1)
где 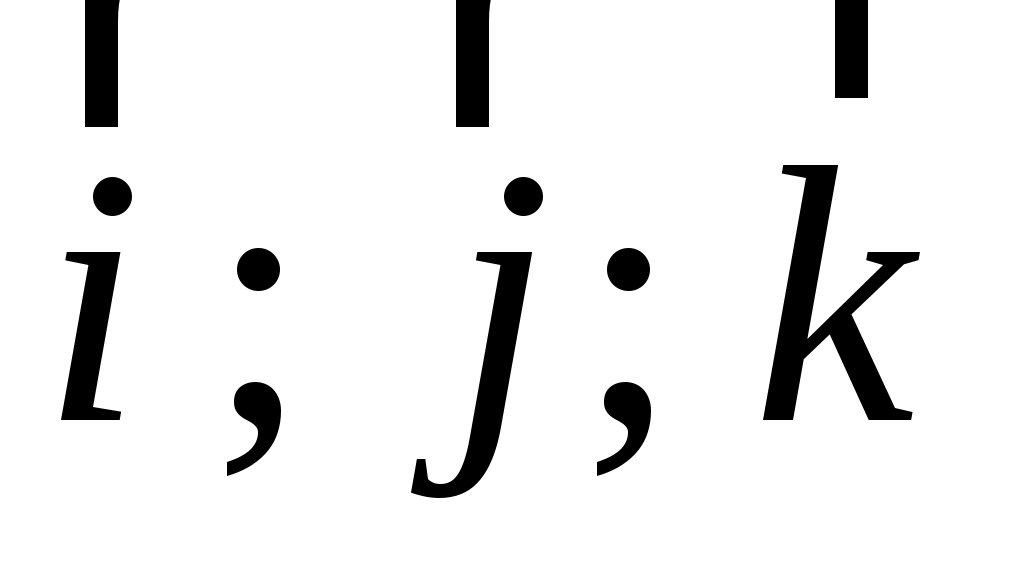 – орты осей координат – орты осей координат 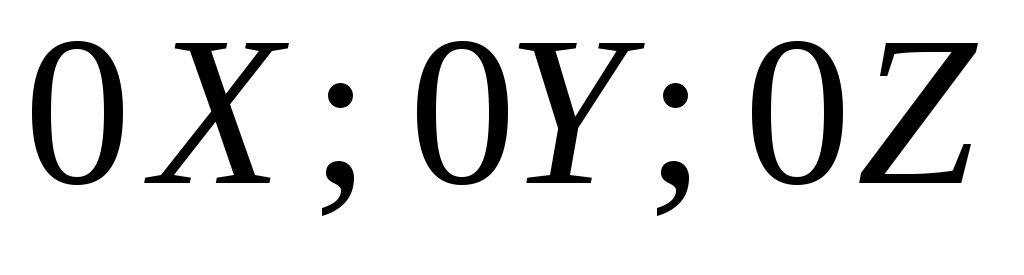 соответственно. соответственно.
При этом модуль радиус-вектора в момент времени 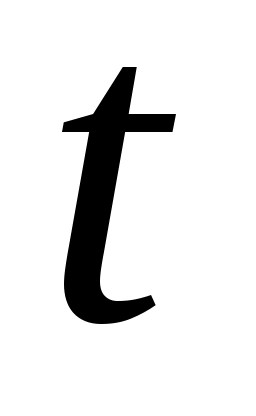 связан с координатами частицы ( связан с координатами частицы (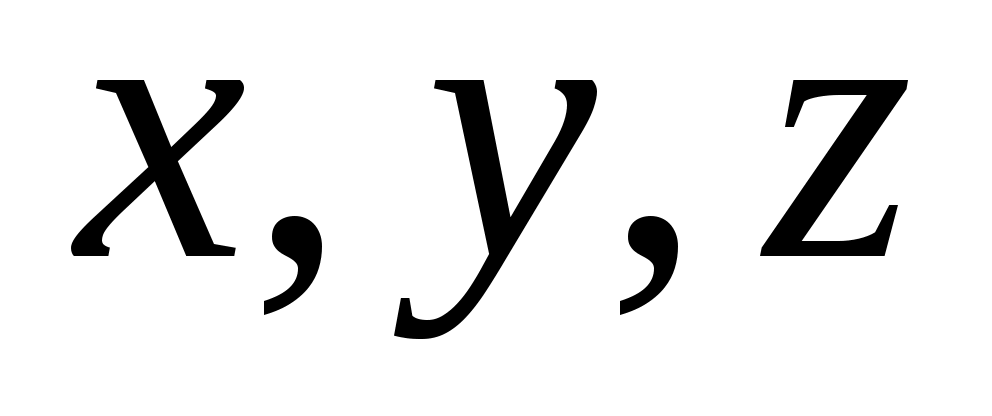 ) следующим образом: ) следующим образом:
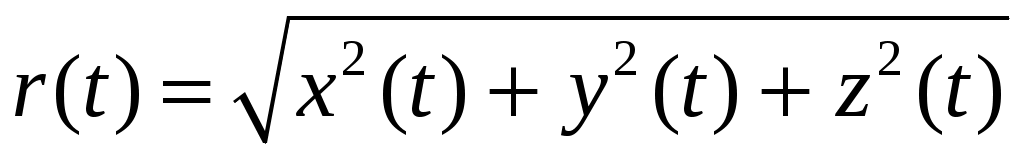 . (1.2) . (1.2)
Зависимости вида
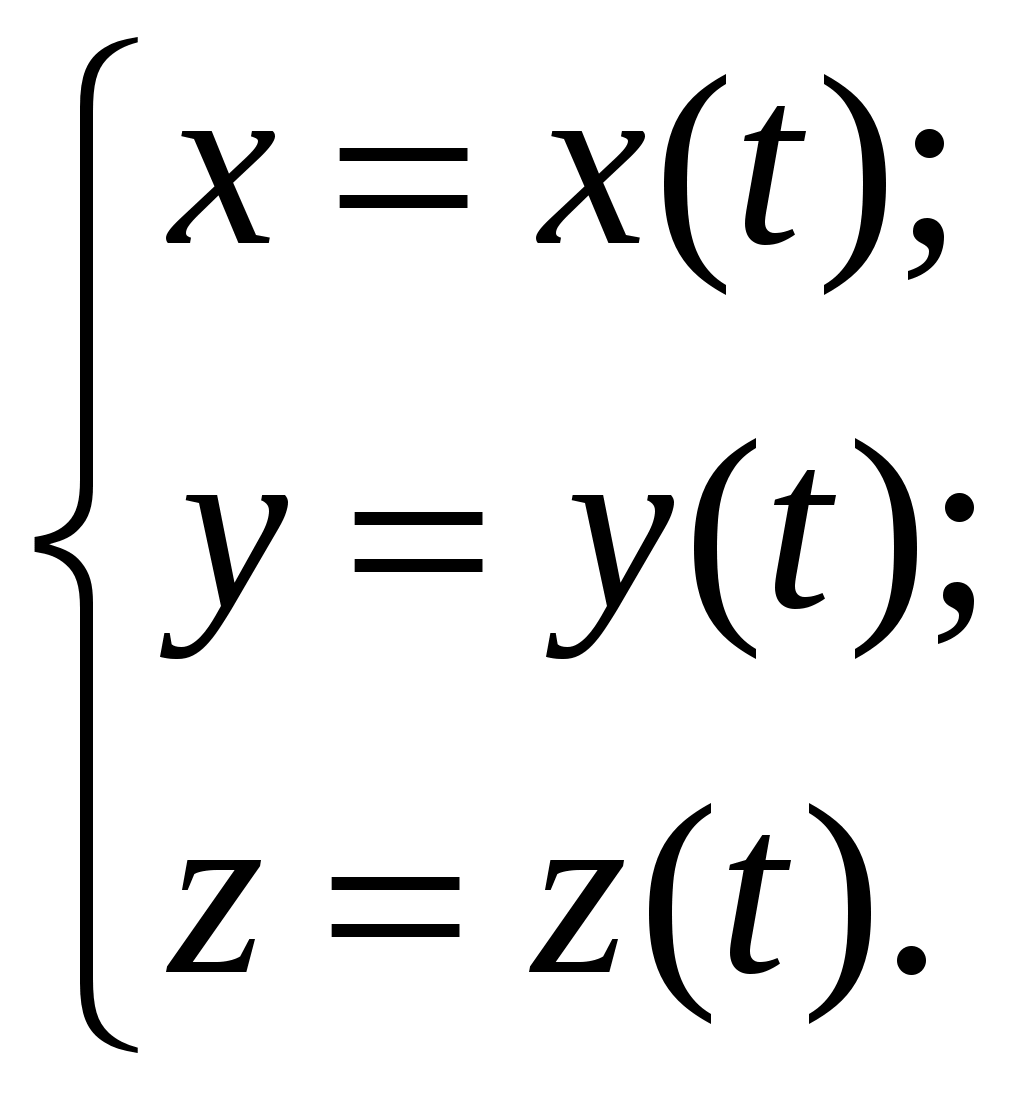
Или
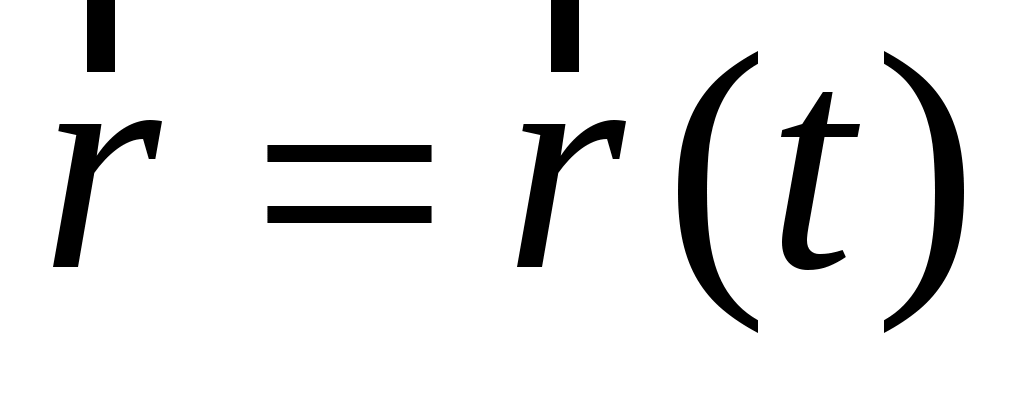 (1.3) (1.3)
называют кинематическими уравнениями движения (координатный и векторный способы задания местоположения частица).
Изменяя свое положение в пространстве с течением времени, частица описывает реальную или воображаемую линию, которая называется траектория. В зависимости от траектории различают прямолинейное и криволинейное движение. Уравнение траектории определяется зависимостью вида
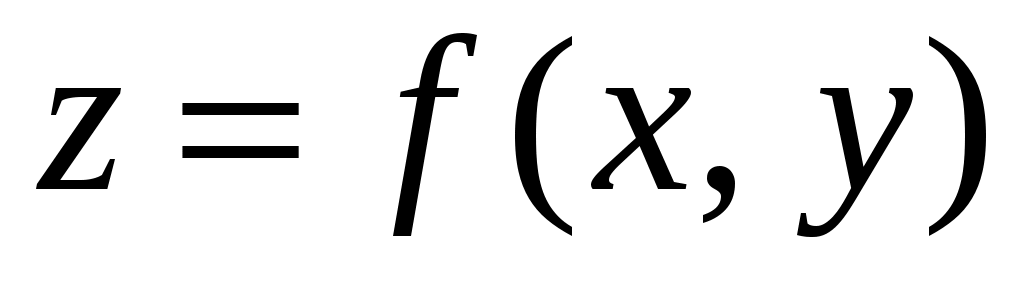 , (1.4) , (1.4)
которую получают из системы уравнений (1.3) путем исключения времени 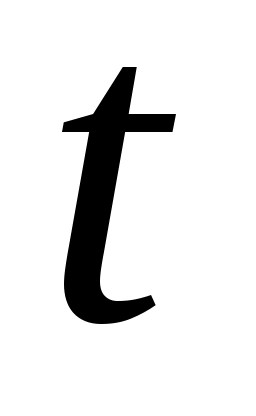 . .
Изменение положения частицы в пространстве за интервал времени 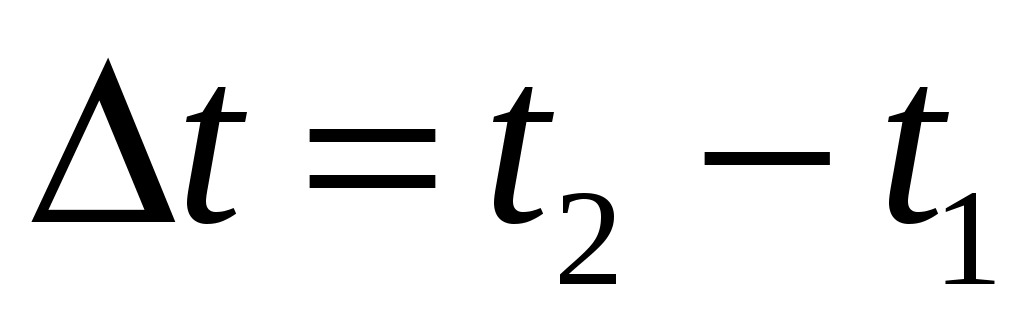 определяет вектор перемещения: определяет вектор перемещения:
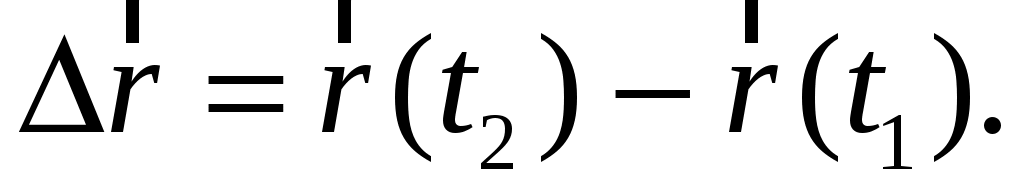 (1.5) (1.5)
Вектор 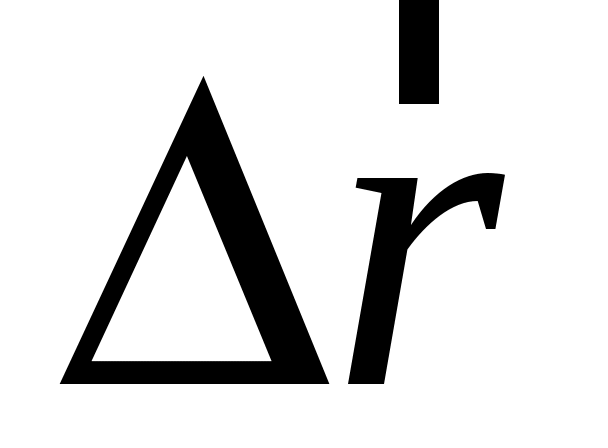 направлен из начальной в конечную точку места нахождения частицы. Модуль направлен из начальной в конечную точку места нахождения частицы. Модуль 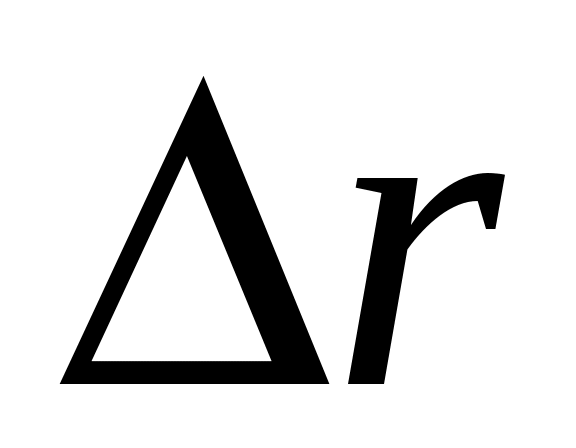 этого вектора и изменение координат частицы этого вектора и изменение координат частицы 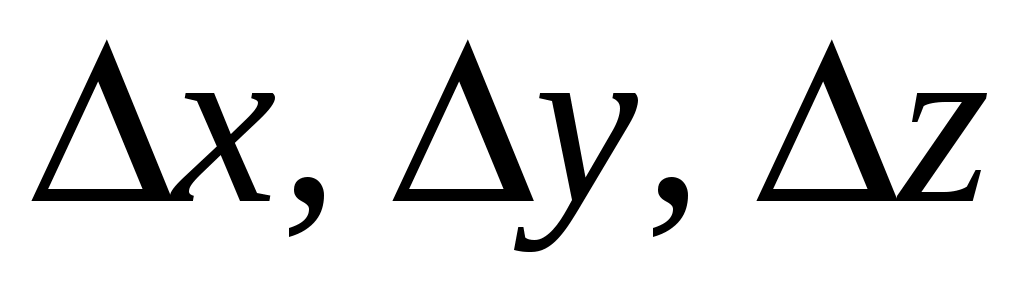 за интервал времени за интервал времени  связаны между собой уравнением: связаны между собой уравнением:
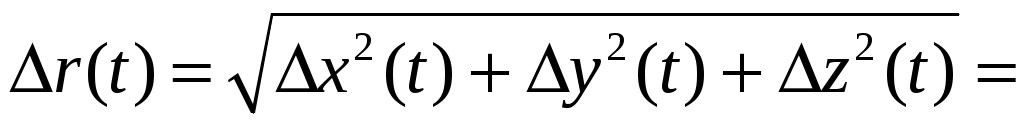
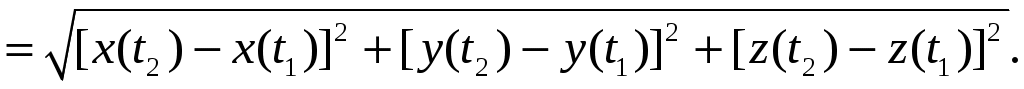 (1.6) (1.6)
Если интервал наблюдения 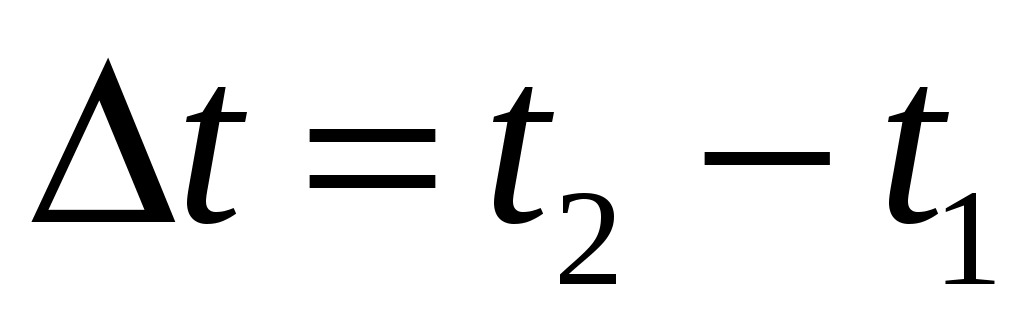 выбрать бесконечно малым и выбрать бесконечно малым и  т.е. т.е. 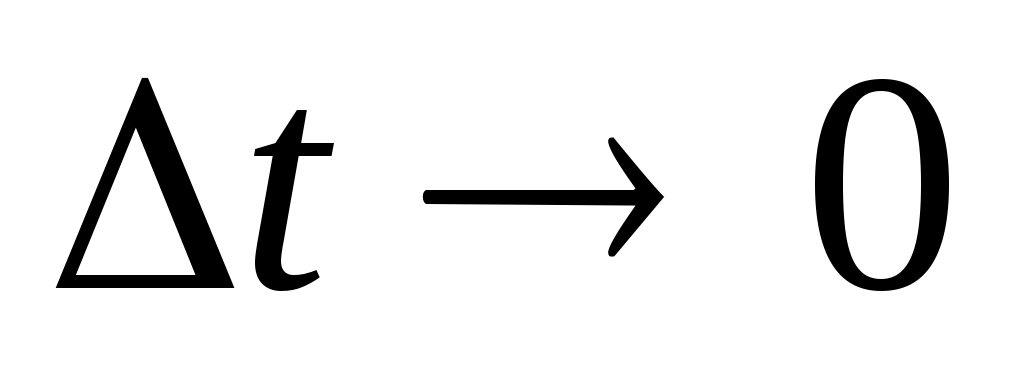 , то соответствующий ему вектор перемещения , то соответствующий ему вектор перемещения 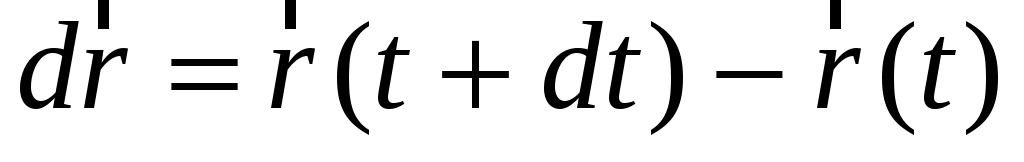 будет направлен по касательной к траектории в данной ее точке. будет направлен по касательной к траектории в данной ее точке.
Для характеристики быстроты изменения от времени вектора перемещения служит вектор мгновенной линейной скорости 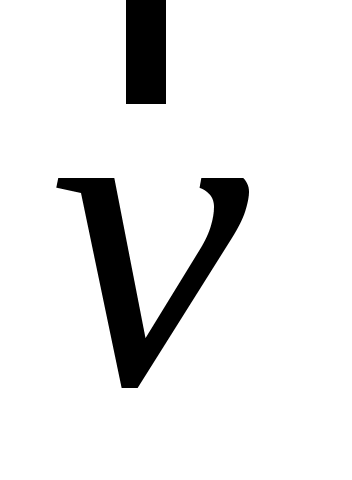 (или просто вектор скорости (или просто вектор скорости 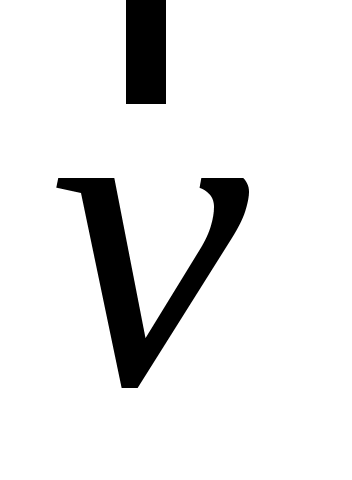 ), который в каждой точке траектории направлен по касательной к ней, т.е. совпадает по направлению с вектором перемещения ), который в каждой точке траектории направлен по касательной к ней, т.е. совпадает по направлению с вектором перемещения 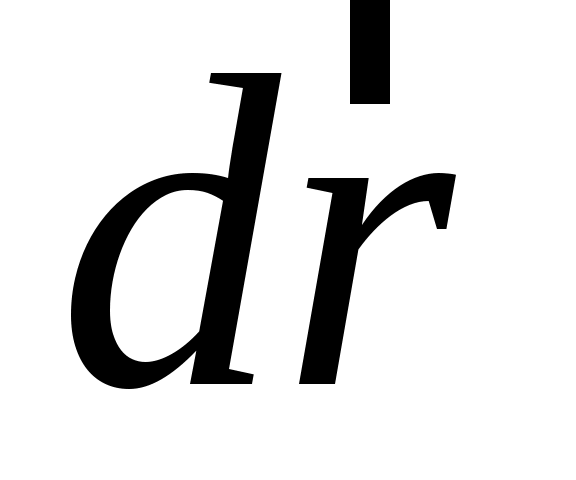 . Если известны зависимости (1.3), то вектор скорости . Если известны зависимости (1.3), то вектор скорости 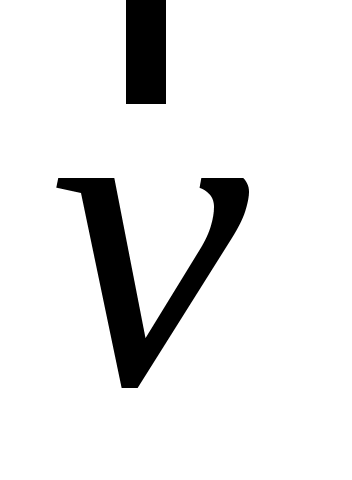 частицы определяется в общем виде как производная от ее радиус-вектора: частицы определяется в общем виде как производная от ее радиус-вектора:
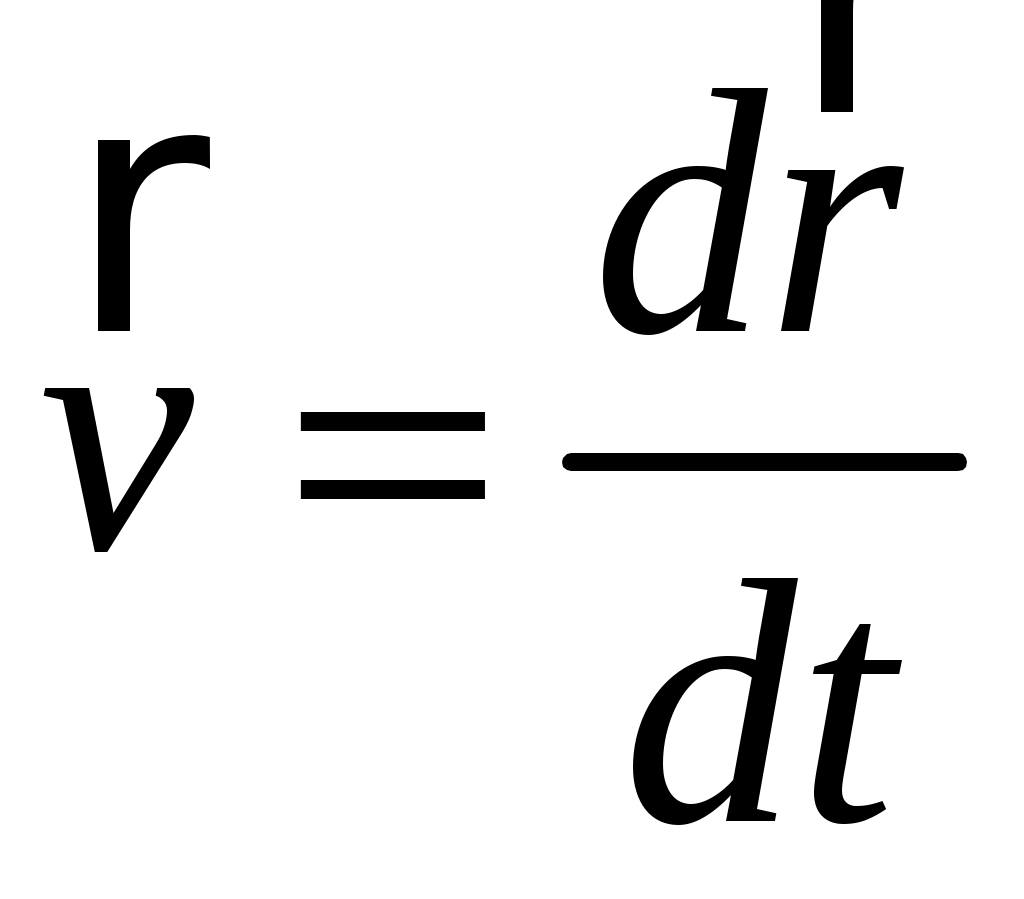 (1.7) (1.7)
или
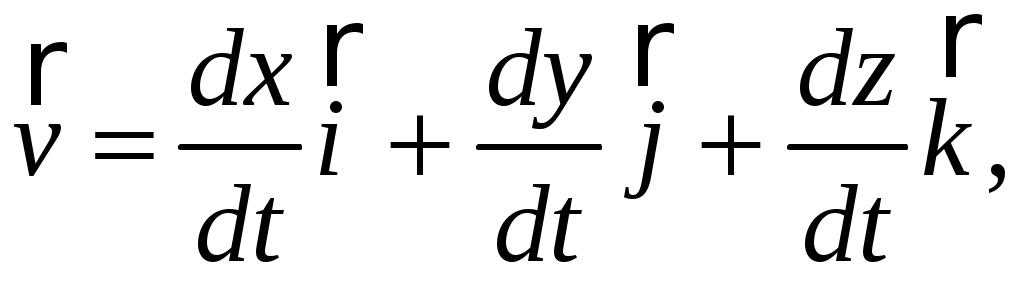 (1.8) (1.8)
где 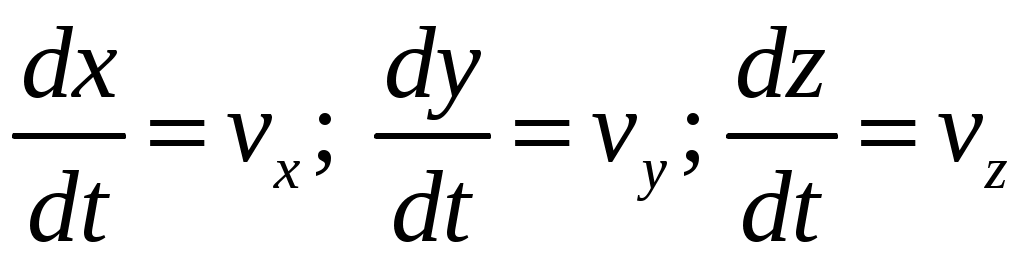 – проекции вектора скорости на оси координат. – проекции вектора скорости на оси координат.
Следовательно, модуль вектора 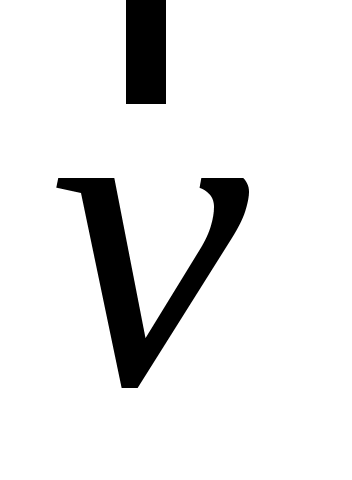 и его проекции на оси координат будут связаны между собой: и его проекции на оси координат будут связаны между собой:
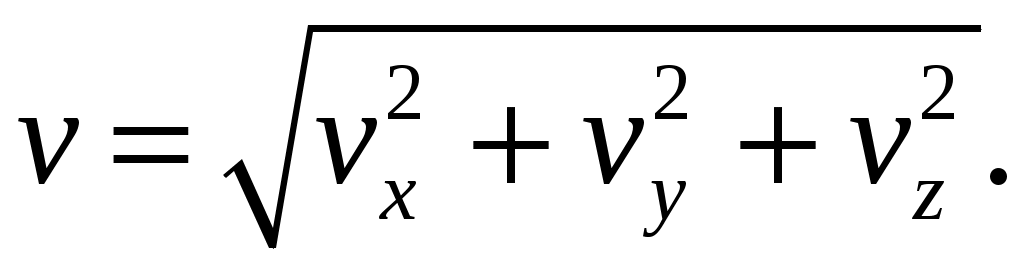 (1.9) (1.9)
Если две частицы движутся со скоростями соответственно 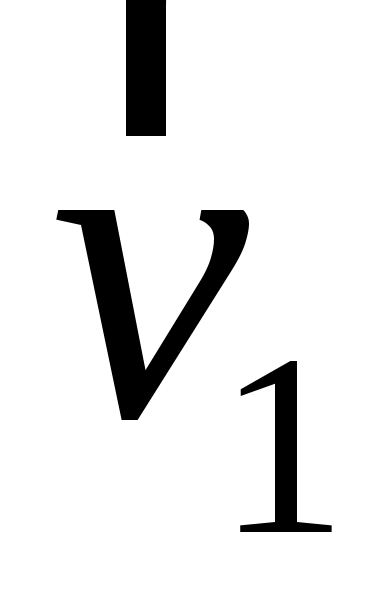 и и 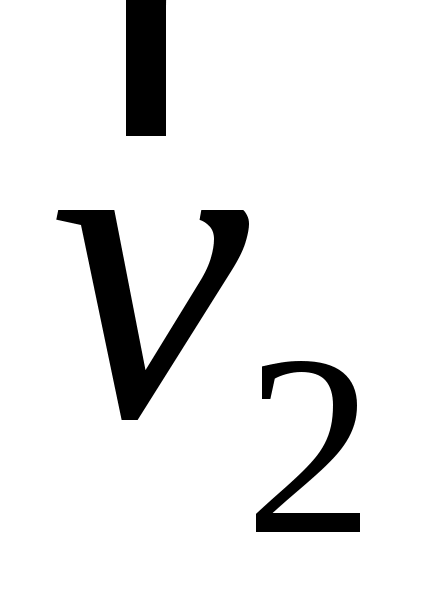 относительно неподвижной системы отсчета, то скорость относительно неподвижной системы отсчета, то скорость 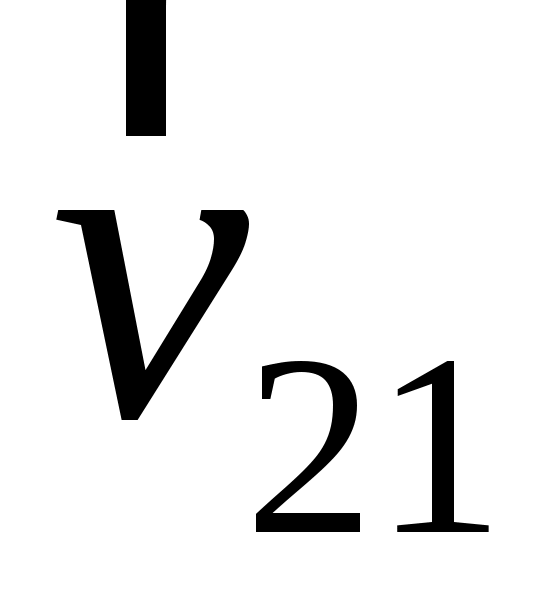 второй частицы по отношению к первой частице будет иметь выражение (закон сложения скоростей в ньютоновской механике): второй частицы по отношению к первой частице будет иметь выражение (закон сложения скоростей в ньютоновской механике):
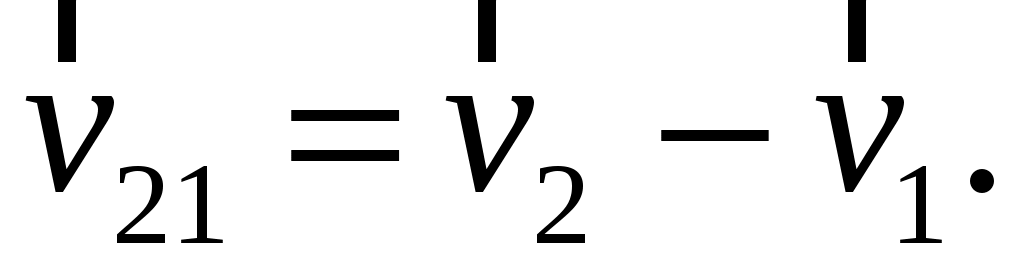 (1.10) (1.10)
Путь S – это длина траектории частицы за время наблюдения 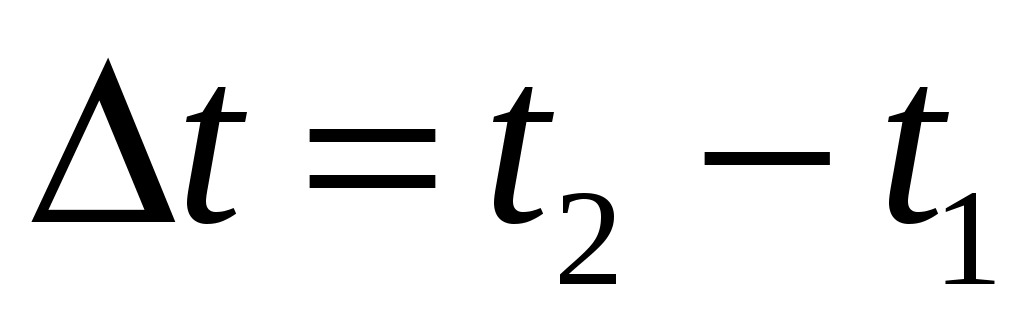 . В случае прямолинейного движения в одну сторону (без разворота) . В случае прямолинейного движения в одну сторону (без разворота)
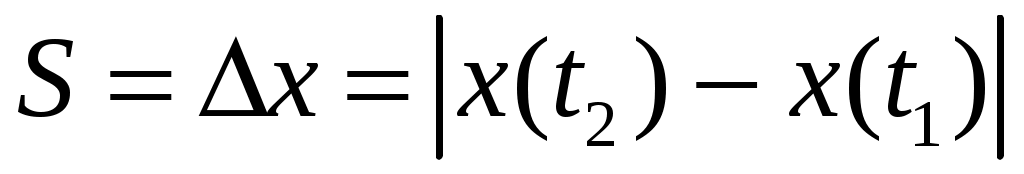 . (1.11) . (1.11)
В выражении (1.11) разность координат взята по модулю, т.к. путь как длина траектории не может быть отрицательным.
Встречаются случаи, когда частица, двигаясь прямолинейно в соответствии с кинематическим уравнением 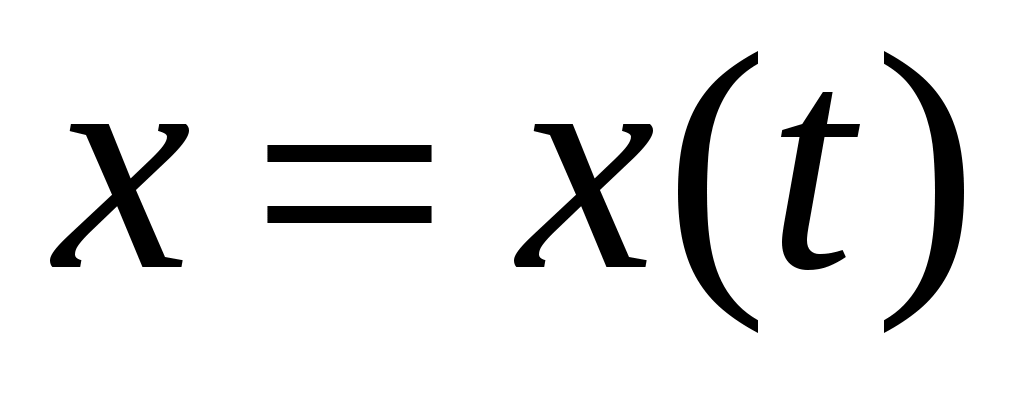 , за время наблюдения , за время наблюдения 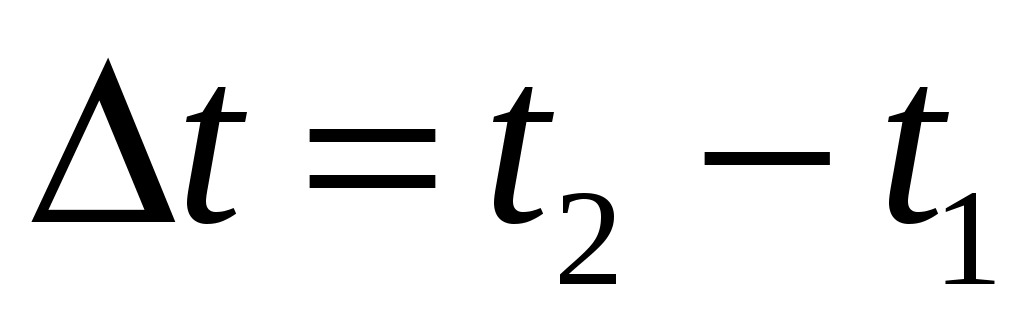 разворачивается в некоторый момент времени разворачивается в некоторый момент времени  и продолжает движение в соответствии с прежним кинематическим уравнением. Тогда путь частицы за все время и продолжает движение в соответствии с прежним кинематическим уравнением. Тогда путь частицы за все время  будет складываться из двух частей: будет складываться из двух частей:
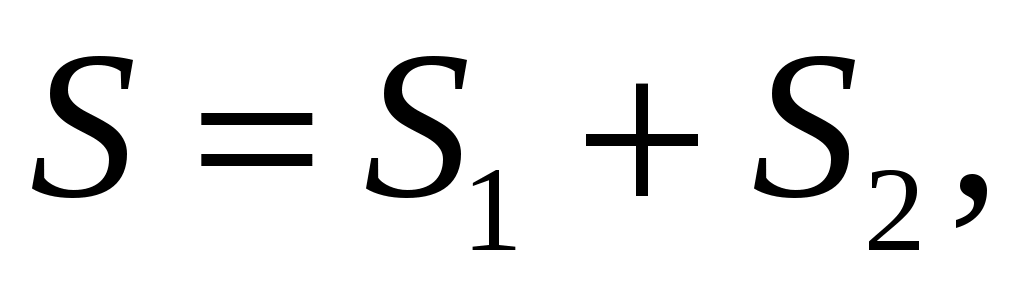
где 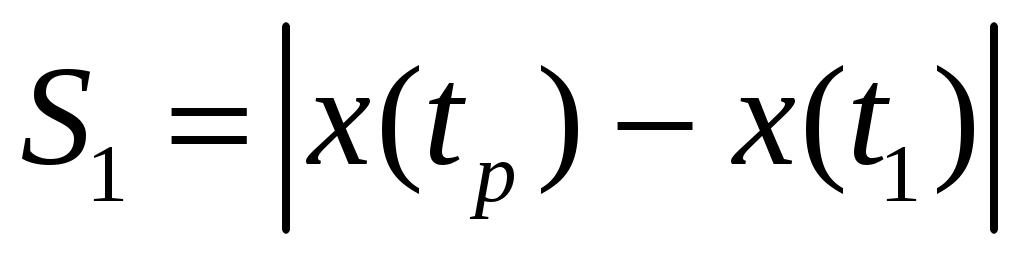 – путь частицы от момента времени – путь частицы от момента времени 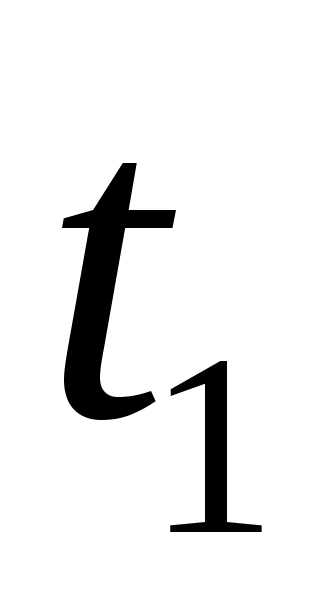 до разворота; до разворота;
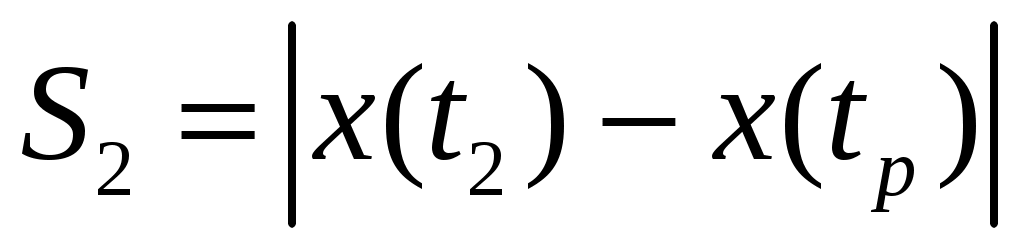 – путь частицы от разворота до момента времени – путь частицы от разворота до момента времени 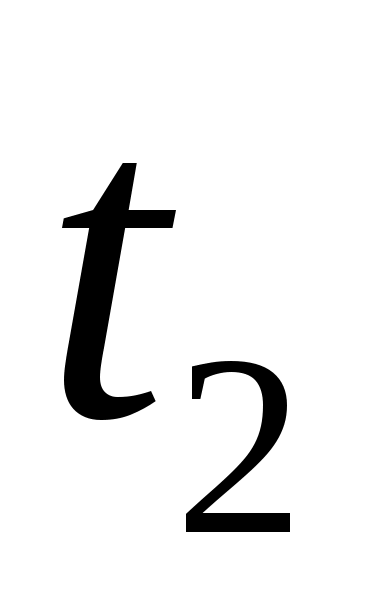 . .
Время разворота 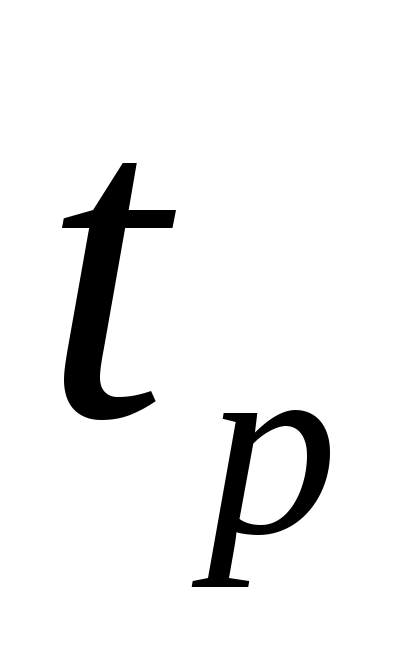 определяется из условия равенства нулю в этот момент времени скорости как неотрицательное решение уравнения: определяется из условия равенства нулю в этот момент времени скорости как неотрицательное решение уравнения:
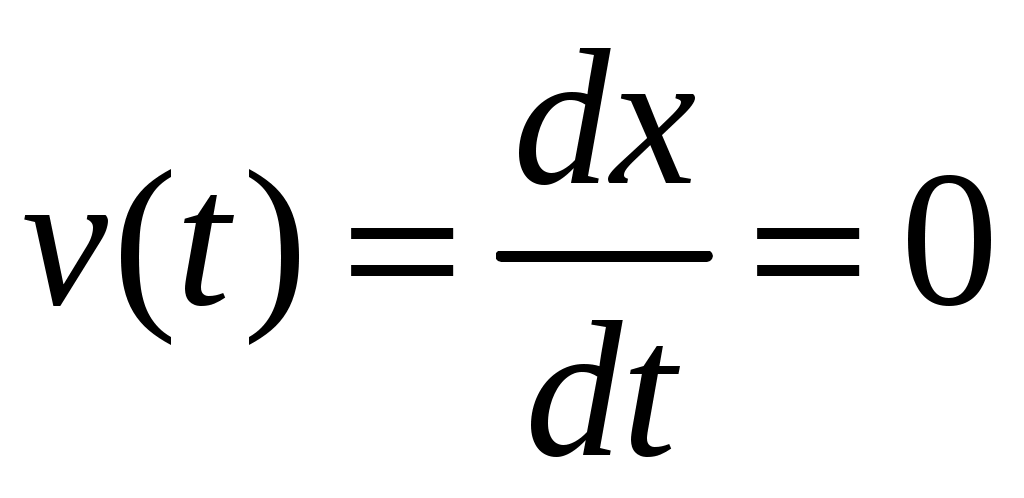 . (1.12) . (1.12)
Если известна зависимость 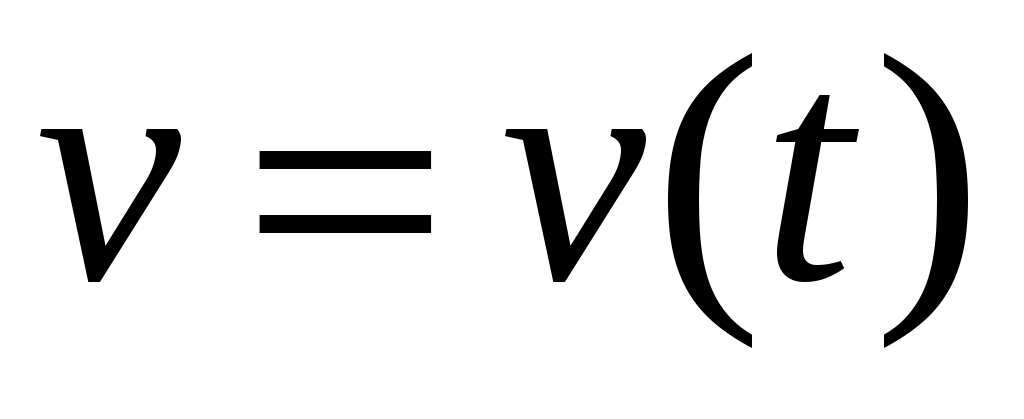 , то пройденный путь можно найти как интеграл: , то пройденный путь можно найти как интеграл:
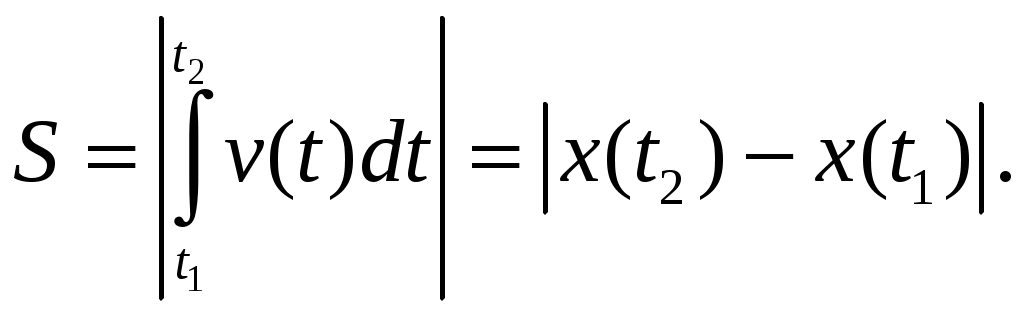 (1.13) (1.13)
Иногда требуется определить модуль векторасредней скорости 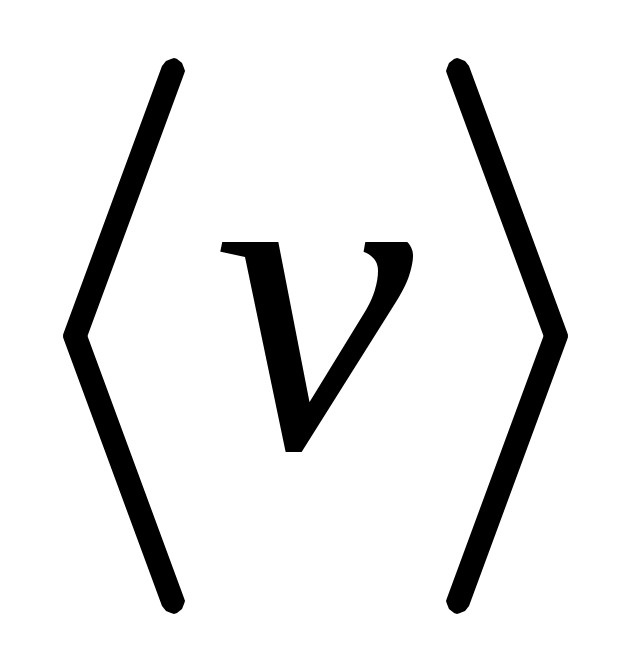 за определенный интервал времени за определенный интервал времени 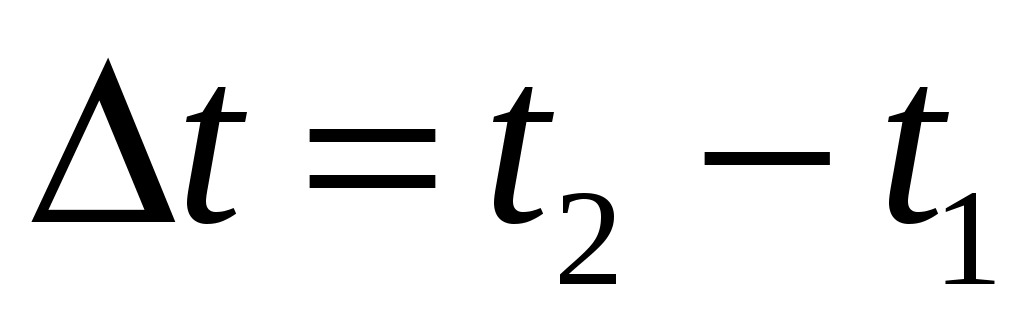 или на отрезке пути или на отрезке пути 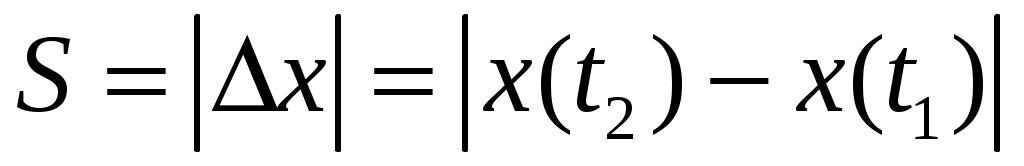 . Часто величину . Часто величину 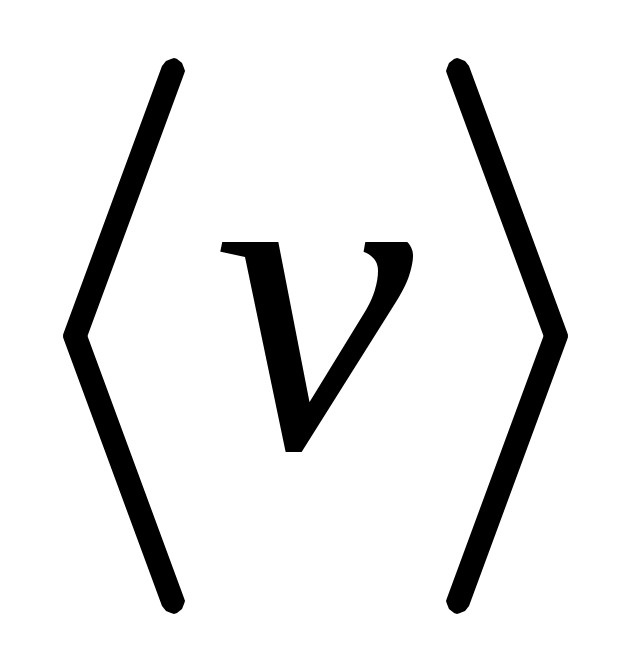 называют средней путевой или просто средней скоростью и находят так: называют средней путевой или просто средней скоростью и находят так:
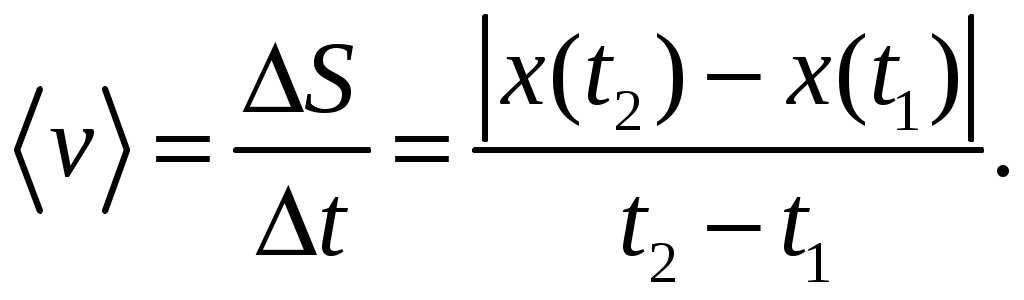 (1.14) (1.14)
Для характеристики быстроты изменения от времени вектора скорости служит вектор мгновенного линейного ускорения 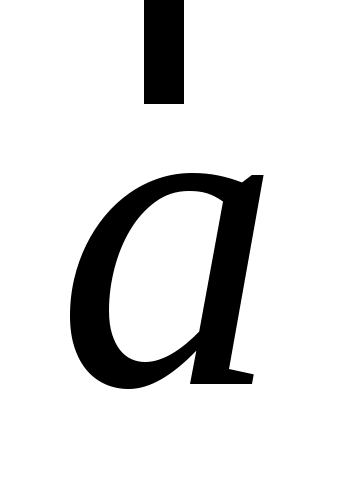 (или просто вектор ускорения (или просто вектор ускорения 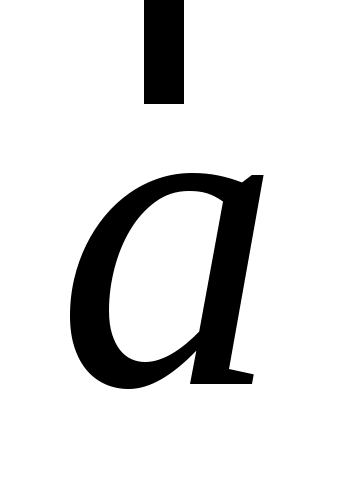 ): ):
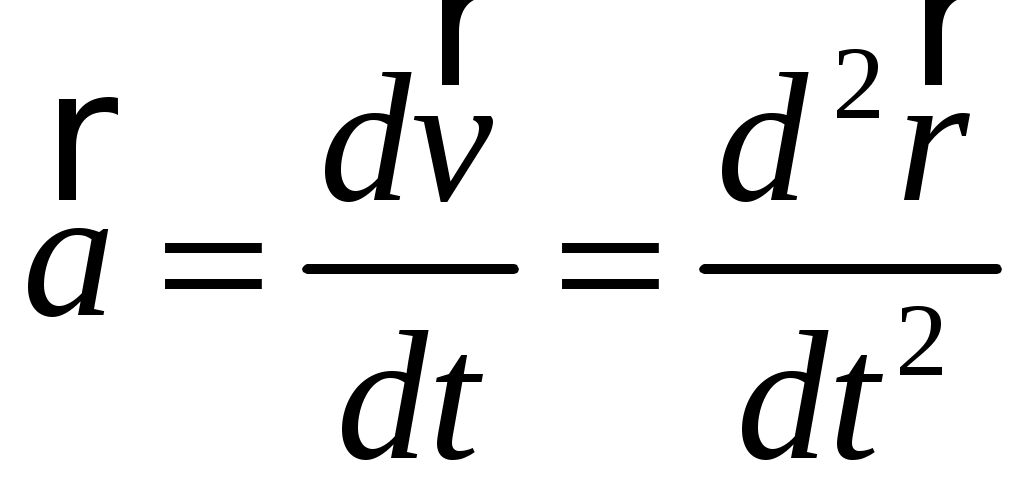 (1.14) (1.14)
или
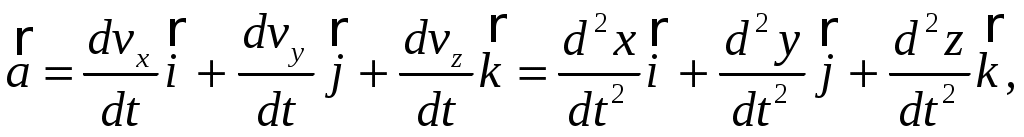 (1.15) (1.15)
где 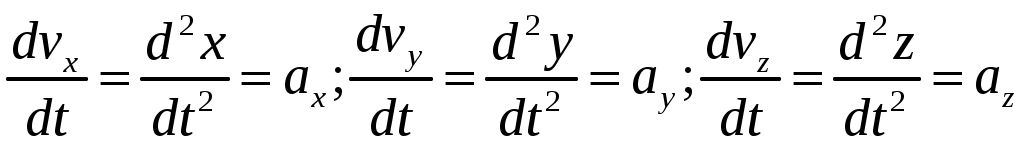 – проекции вектора ускорения на оси координат. – проекции вектора ускорения на оси координат.
Модуль вектора 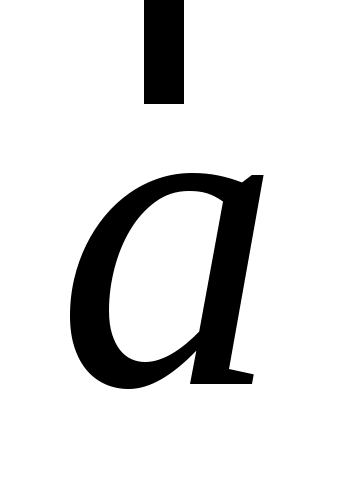 и его проекции на оси координат связаны между собой: и его проекции на оси координат связаны между собой:
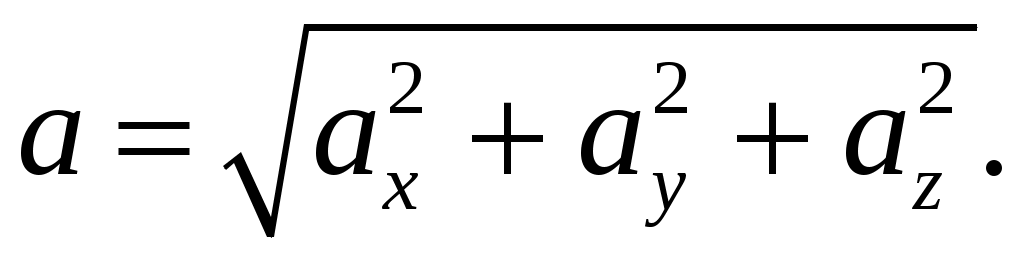 (1.16) (1.16)
Часто в заданиях требуется определить модуль среднего ускорения за некоторый промежуток времени 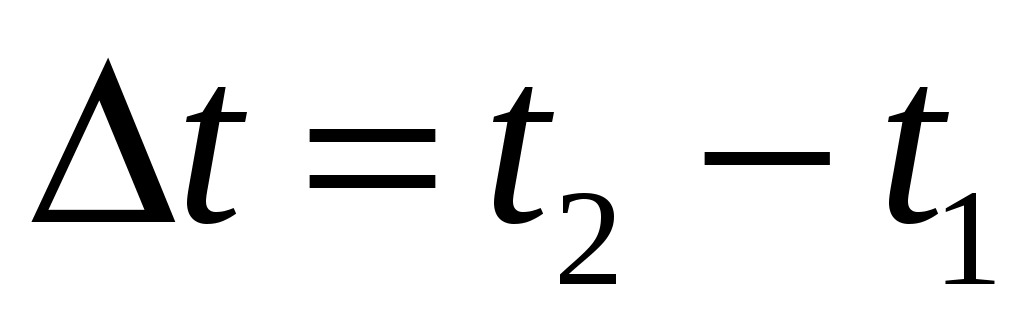 : :
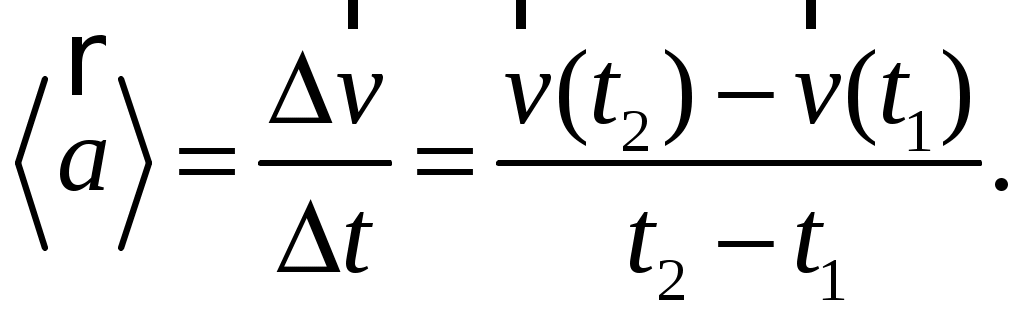 (1.17) (1.17)
Кинематика вращательного движения
При вращательном движении твердого тела для задания его положения в пространстве в зависимости от времени используют кинематическое уравнение, определяющее зависимость угла поворота  любой точки тела вокруг оси вращения от времени любой точки тела вокруг оси вращения от времени 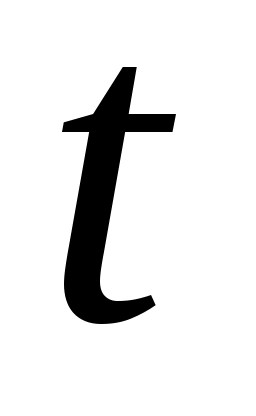 вида вида
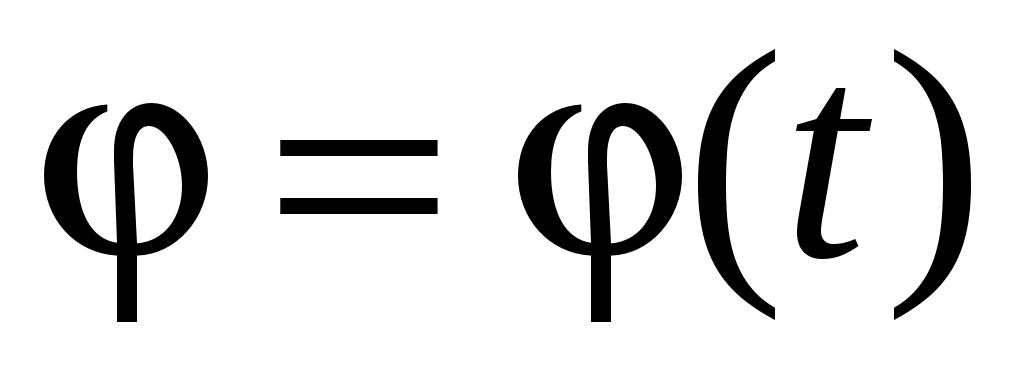 . .
В этом случае мерой перемещения за элементарный промежуток времени  служит вектор элементарного поворота служит вектор элементарного поворота 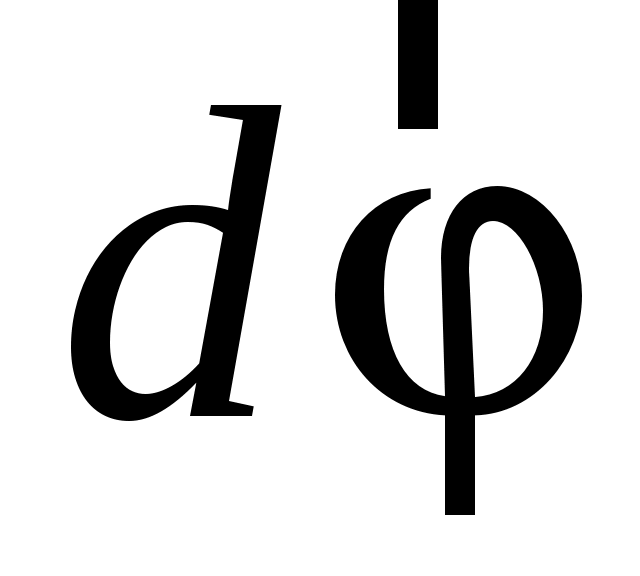 . По модулю он равен углу . По модулю он равен углу 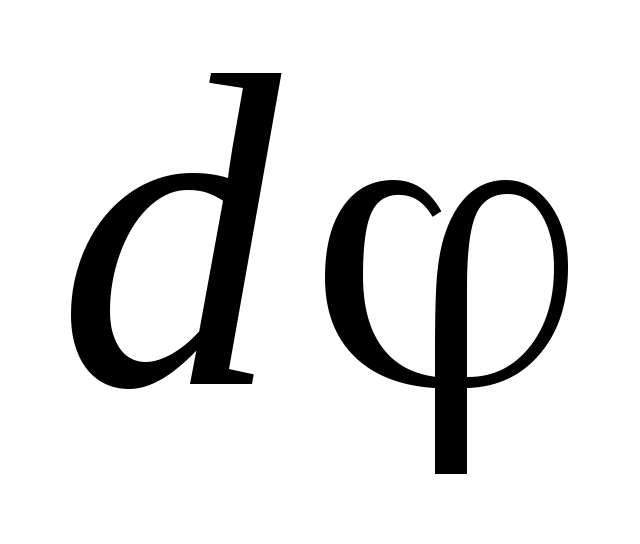 поворота частицы вокруг оси за время поворота частицы вокруг оси за время  и направлен вдоль оси вращения по правилу правого винта (рисунок 1.1; а – вращение против часовой стрелки, б – вращение по часовой стрелке). и направлен вдоль оси вращения по правилу правого винта (рисунок 1.1; а – вращение против часовой стрелки, б – вращение по часовой стрелке).
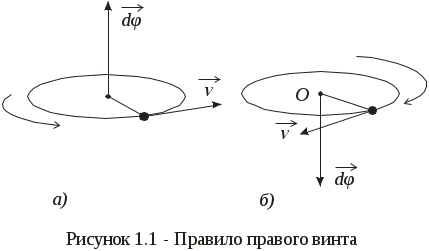
Характеристикой направления быстроты вращения тела служит вектор угловой скорости:
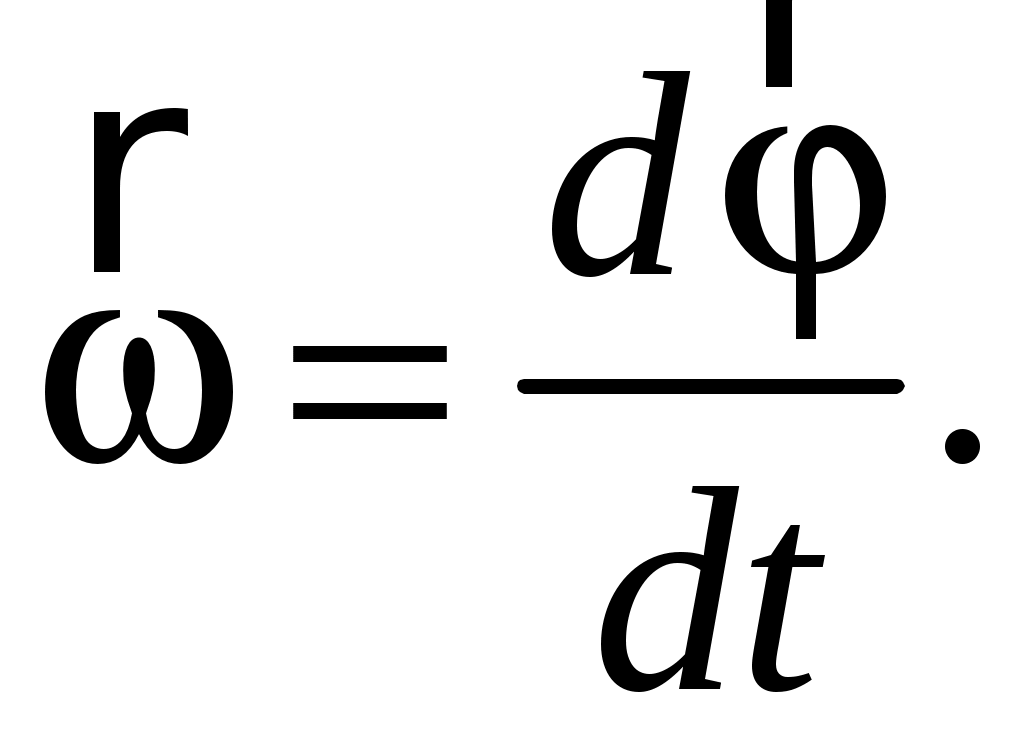 (1.18) (1.18)
Вектор 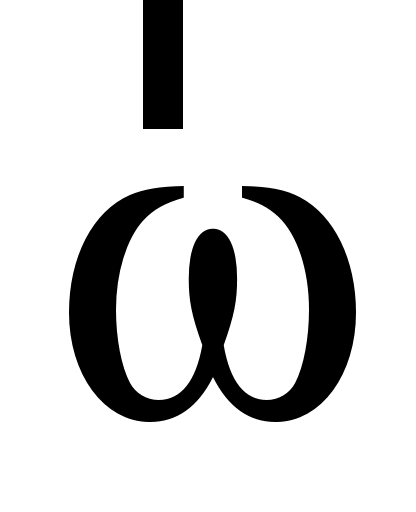 по направлению совпадает с вектором по направлению совпадает с вектором 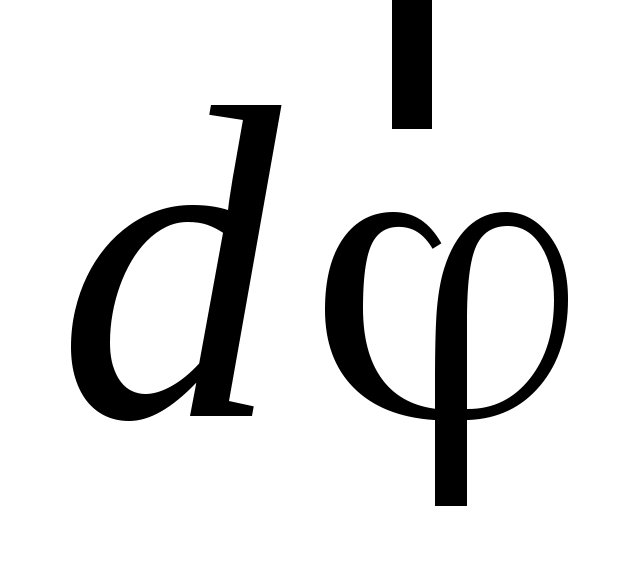 . .
В общем случае угол поворота при известной угловой скорости в соответствии с выражением (1.18) можно определить как интеграл:
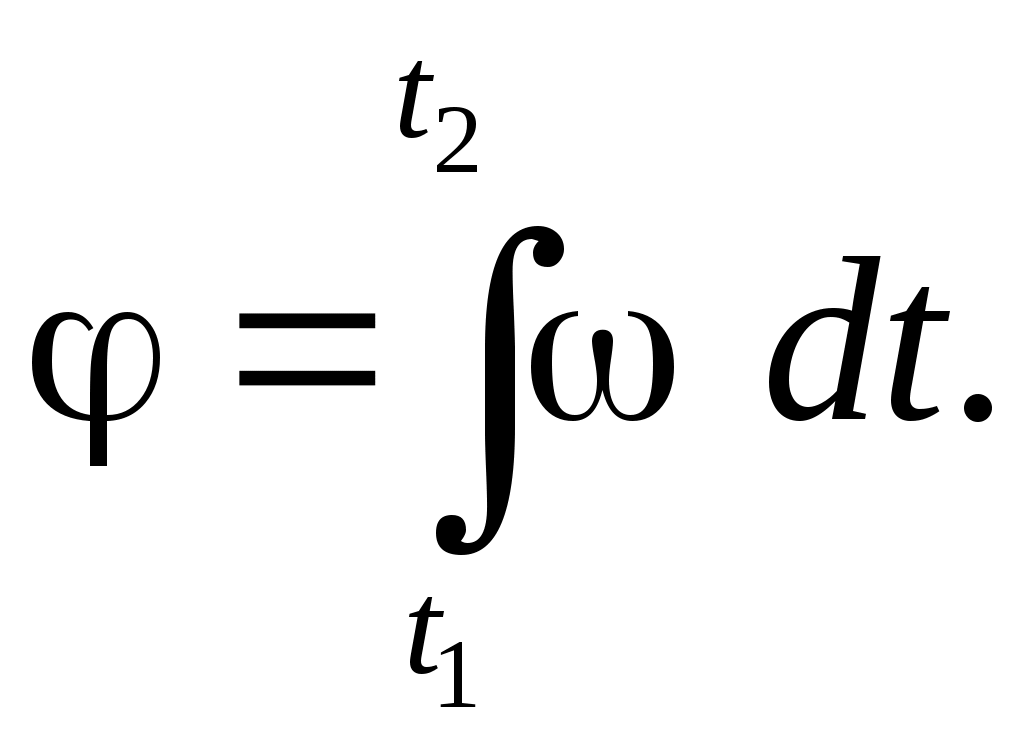
Модули векторов линейной и угловой скоростей связаны между собой:
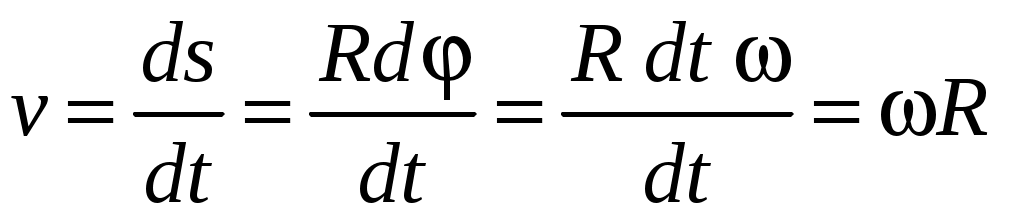 . (1.19) . (1.19)
Для характеристики быстроты изменения вектора угловой скорости используют вектор углового ускорения:
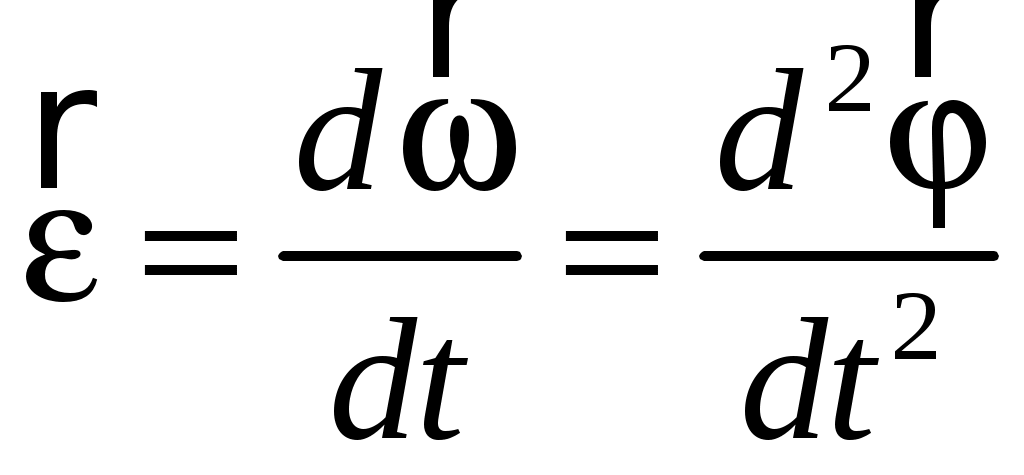 . (1.20) . (1.20)
При криволинейном движении вектор линейного ускорения  направлен в сторону вогнутости траектории и лежит в плоскости движения частицы (рисунок 1.2). В этой плоскости вектор ускорения принято разлагать на две ортогональные составляющие направлен в сторону вогнутости траектории и лежит в плоскости движения частицы (рисунок 1.2). В этой плоскости вектор ускорения принято разлагать на две ортогональные составляющие 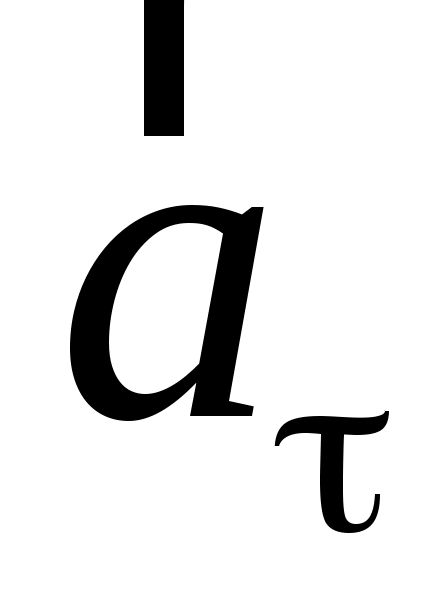 и и 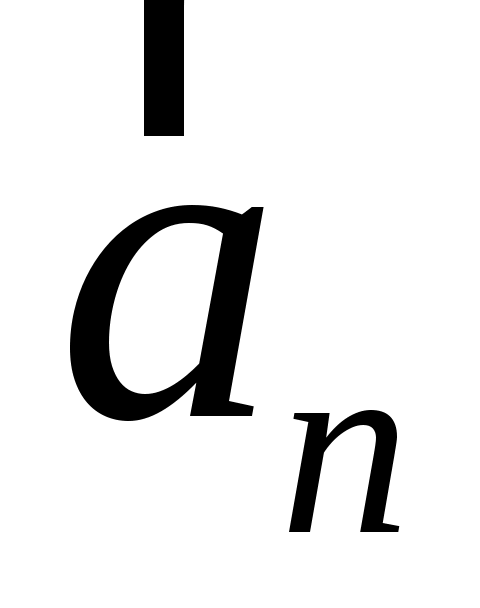 , т.е. , т.е.
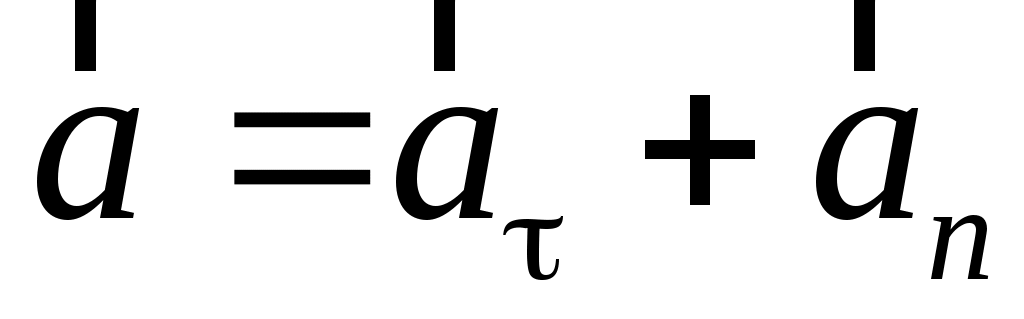 . .
или
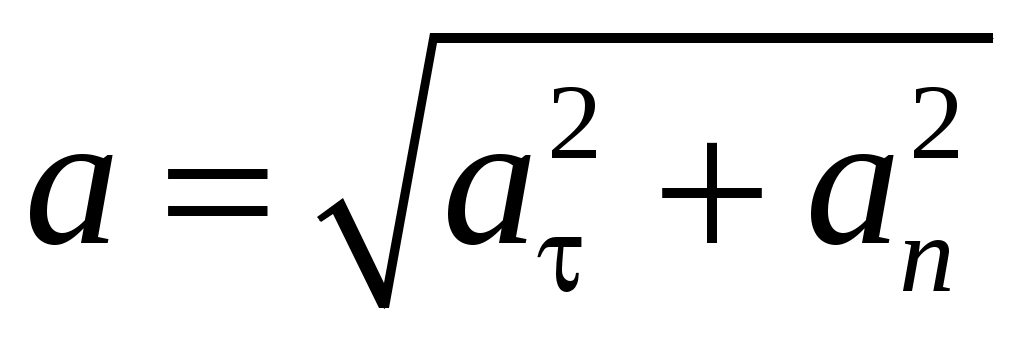 . (1.21) . (1.21)
С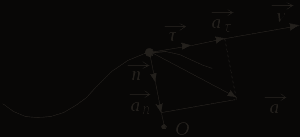 оставляющая оставляющая 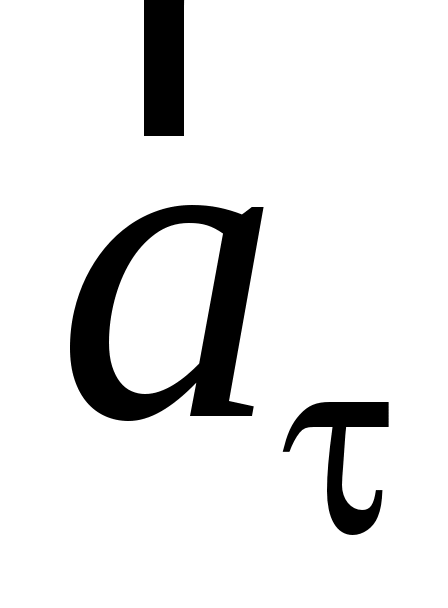 называется касательным (тангенциальным) ускорением частицы. Оно направлено по касательной к траектории в данной ее точке. называется касательным (тангенциальным) ускорением частицы. Оно направлено по касательной к траектории в данной ее точке.
Вектор касательного ускорения имеет выражение:
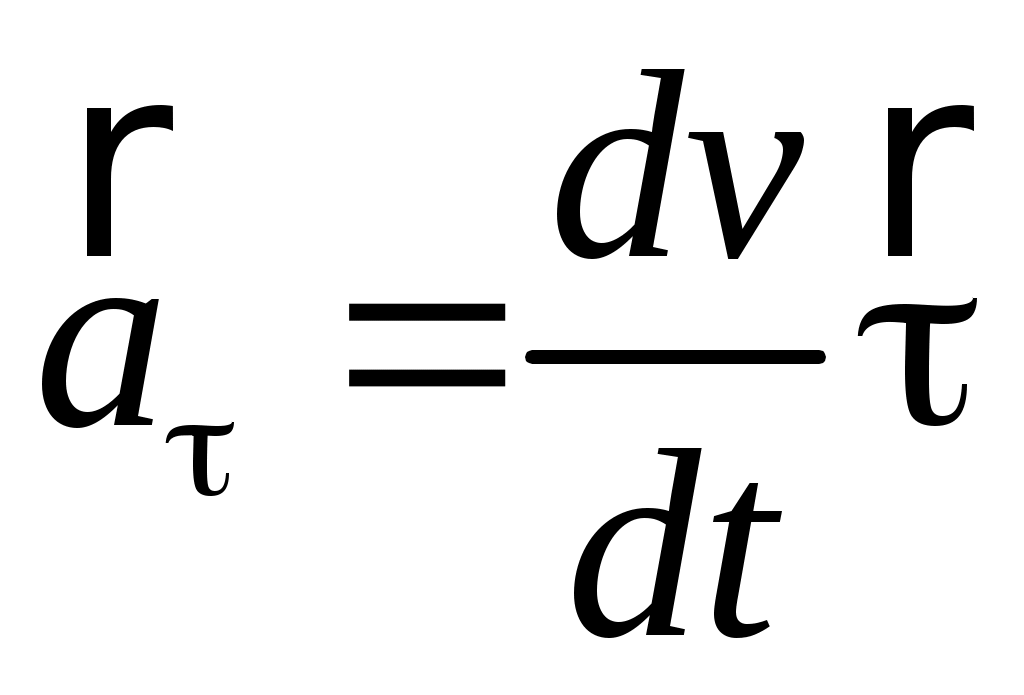 , (1.22) , (1.22)
где 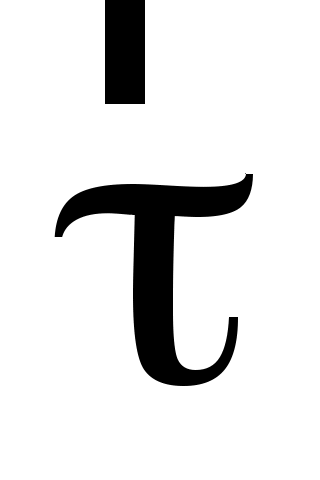 – орт касательной, проведенной в данной точке траектории по направлению вектора – орт касательной, проведенной в данной точке траектории по направлению вектора 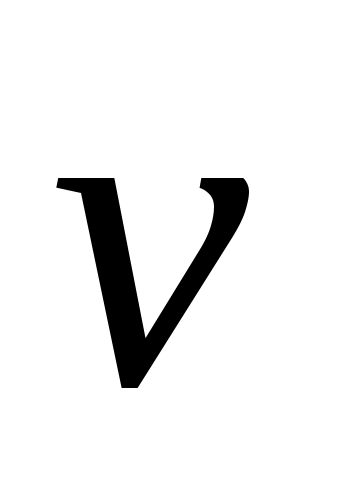 . Касательное ускорение . Касательное ускорение 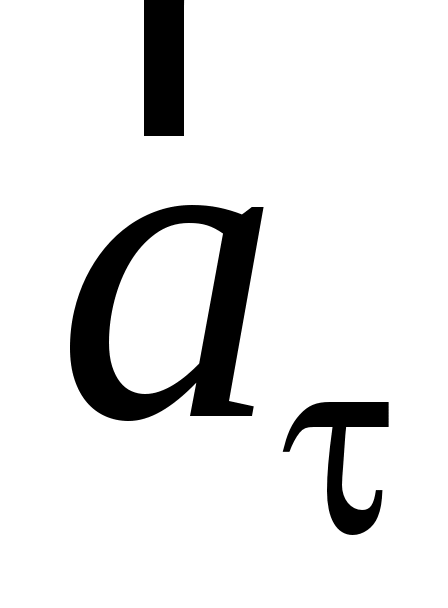 характеризует быстроту изменения модуля вектора скорости частицы. характеризует быстроту изменения модуля вектора скорости частицы.
В соответствии с выражением (1.19) модули касательного и углового ускорения связаны между собой:
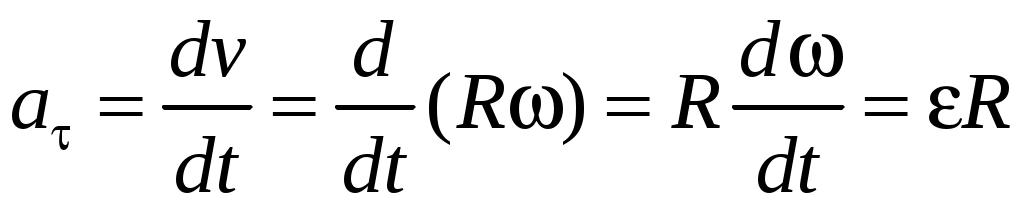 . (1.23) . (1.23)
Составляющая 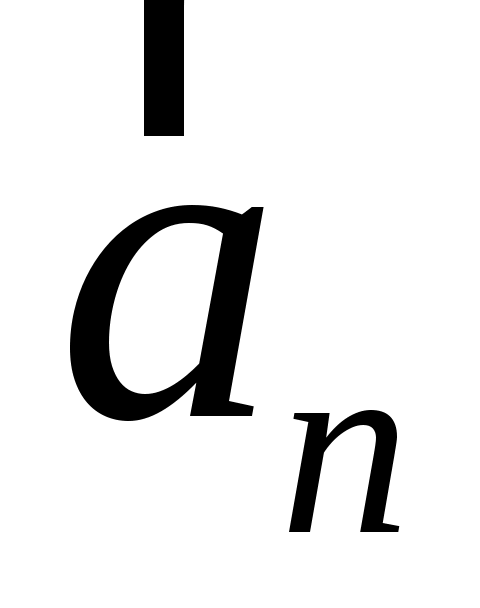 называется нормальным (центростремительным) ускорением частицы. Оно направлено по нормали (перпендикулярно к касательной) в данной точке траектории в сторону центра ее кривизны. Вектор нормального ускорения имеет выражение: называется нормальным (центростремительным) ускорением частицы. Оно направлено по нормали (перпендикулярно к касательной) в данной точке траектории в сторону центра ее кривизны. Вектор нормального ускорения имеет выражение:
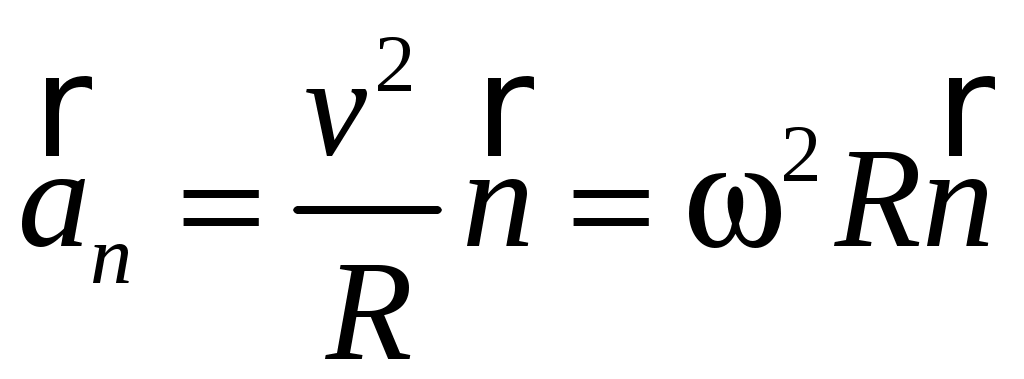 , (1.24) , (1.24)
где 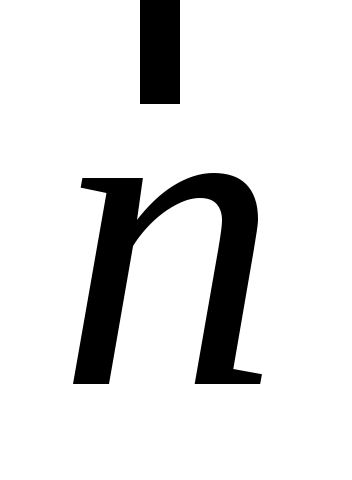 – орт нормали; – орт нормали;
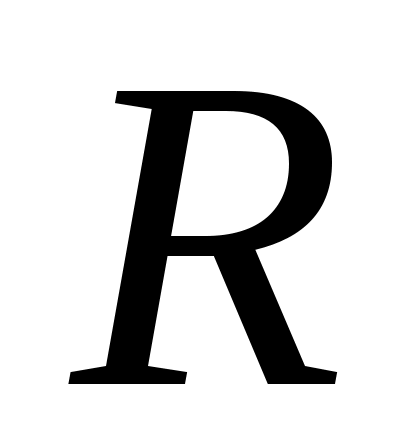 – радиус кривизны траектории в данной точке. – радиус кривизны траектории в данной точке.
Нормальное ускорение 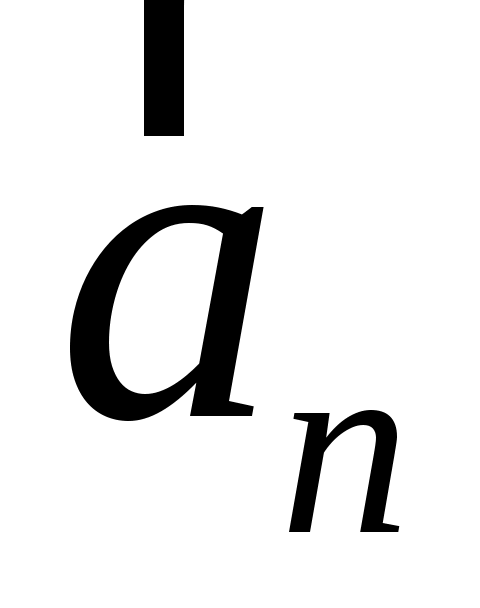 характеризует быстроту изменения направления вектора линейной скорости частицы. характеризует быстроту изменения направления вектора линейной скорости частицы.
Модуль вектора 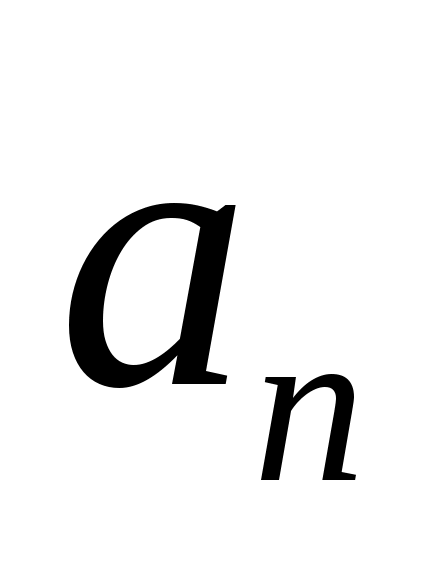 : :
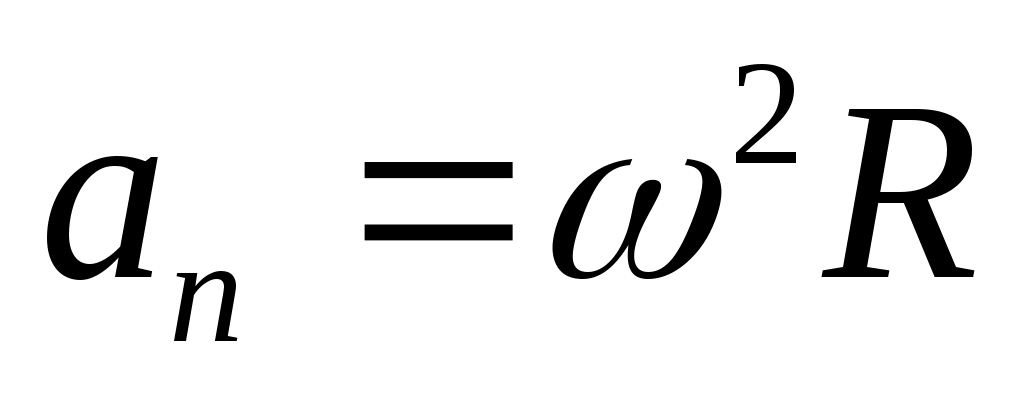 . .
1.2. Примеры выполнения тестовых заданий
Кинематика поступательного движения
Задание 1.
Если движение частицы в плоскости 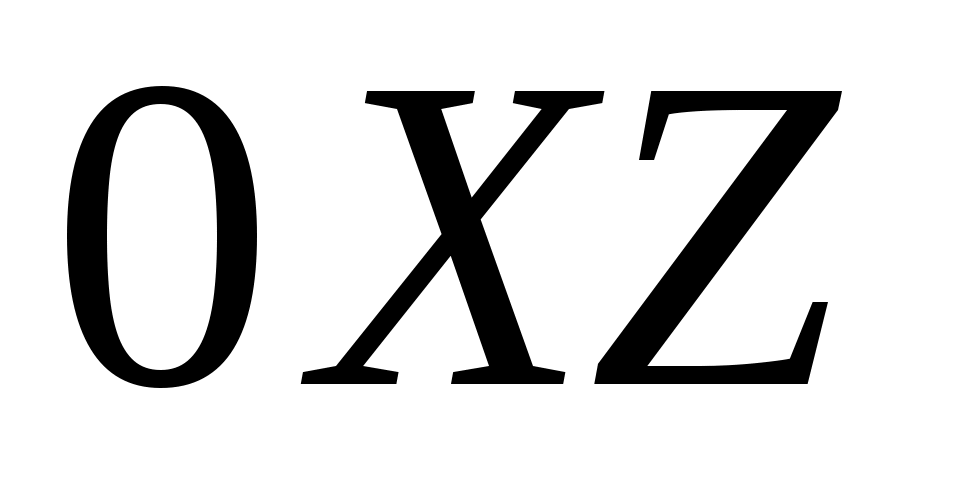 описывается уравнениями описывается уравнениями 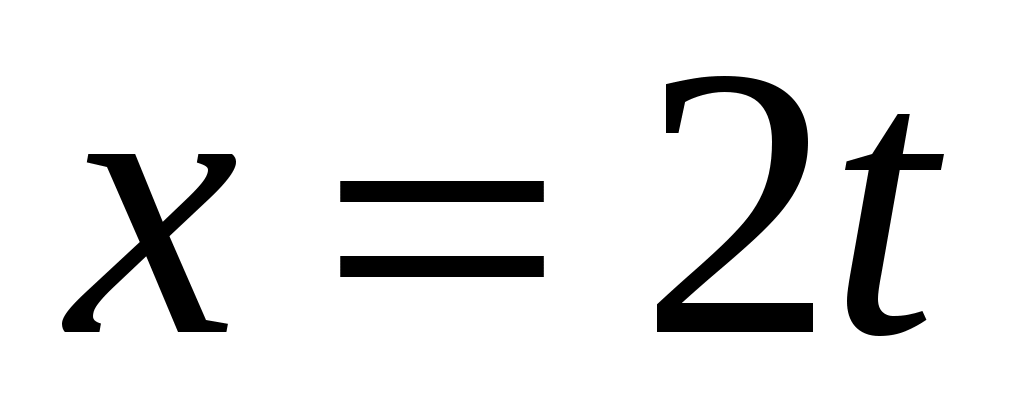 (м); (м); 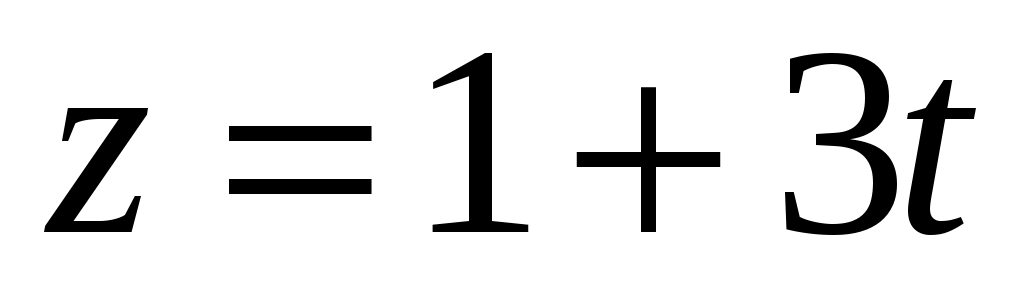 (м), то выражение радиус-вектора частицы будет иметь вид (м), то выражение радиус-вектора частицы будет иметь вид
|
1) 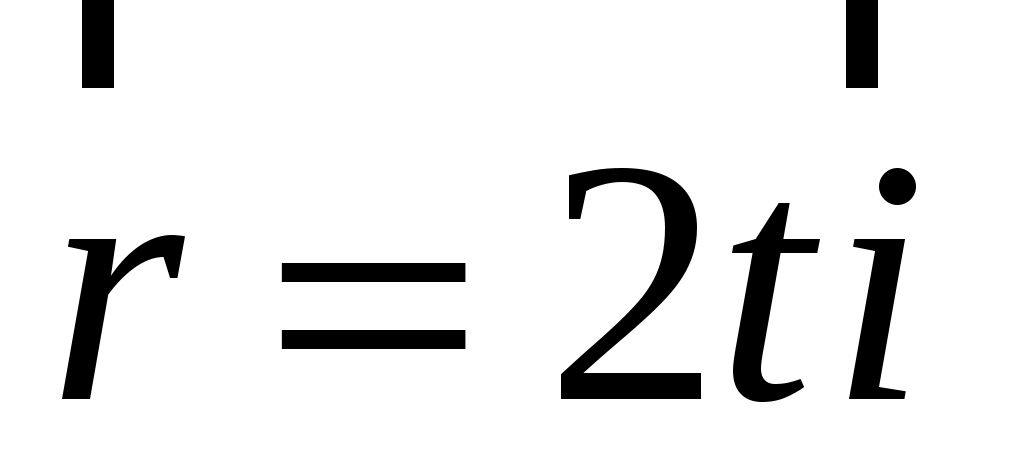 ; ;
|
2)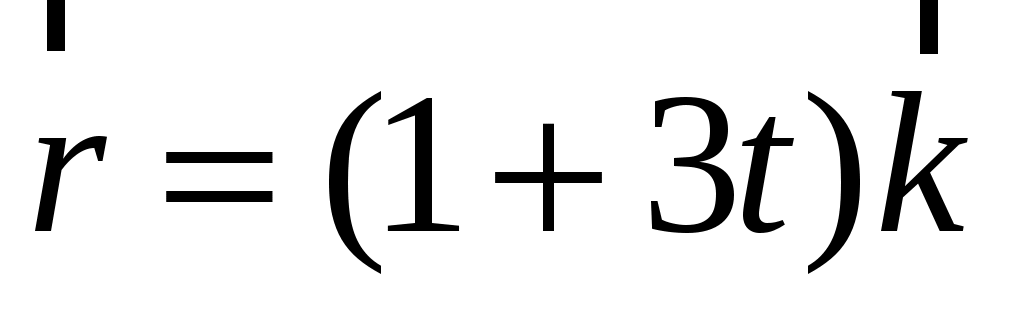 ; ;
|
3)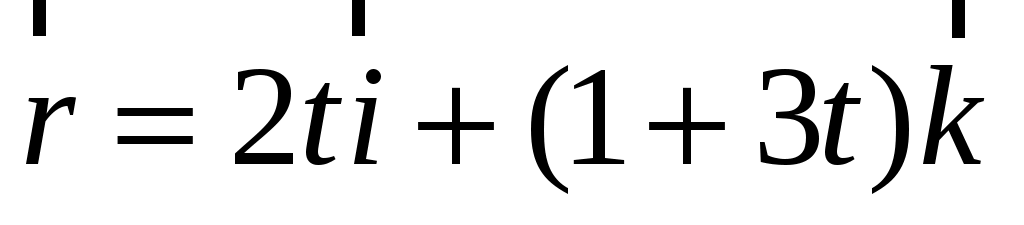 ; ;
|
4)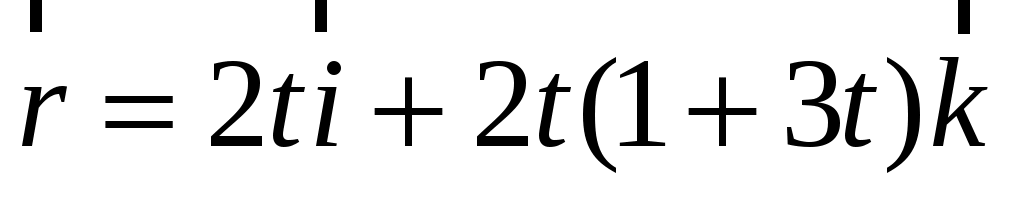 . .
|
Дано:
|
Решение:
|
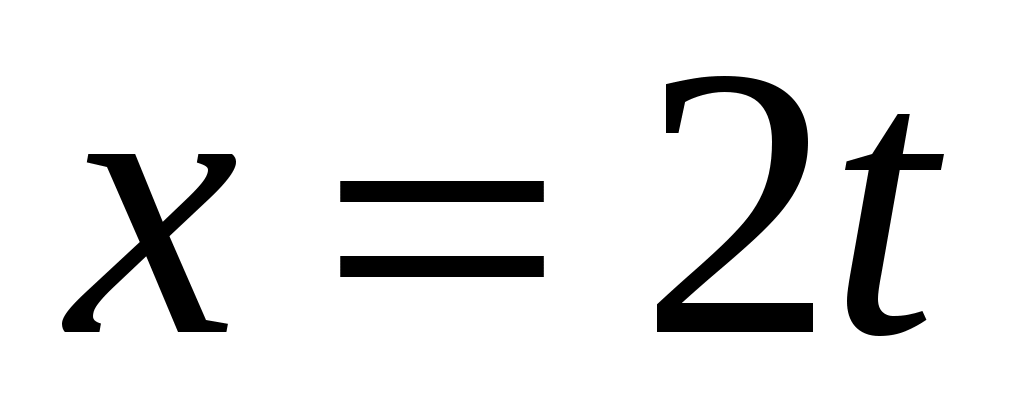 (м) (м)
|
В соответствии с выражением (1.1) ортогональное разложение радиус-вектора имеет вид:
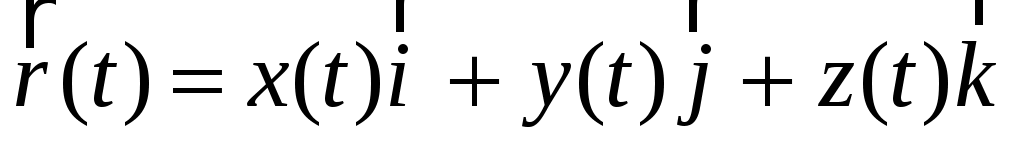 . (1) . (1)
|
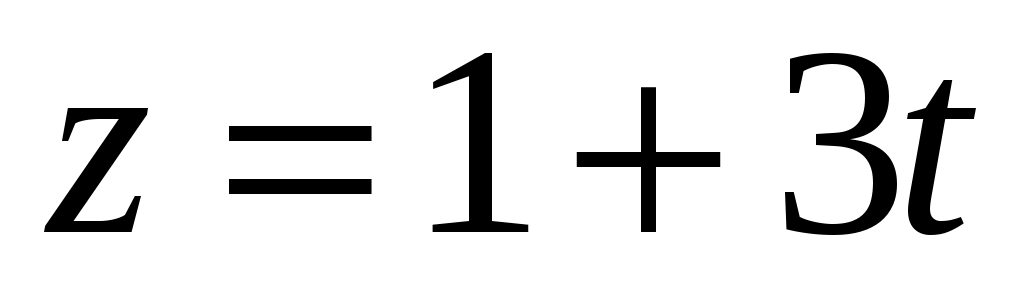 (м) (м)
|
 ? ?
|
Сравнивая это выражение с исходными данными, заметим, что 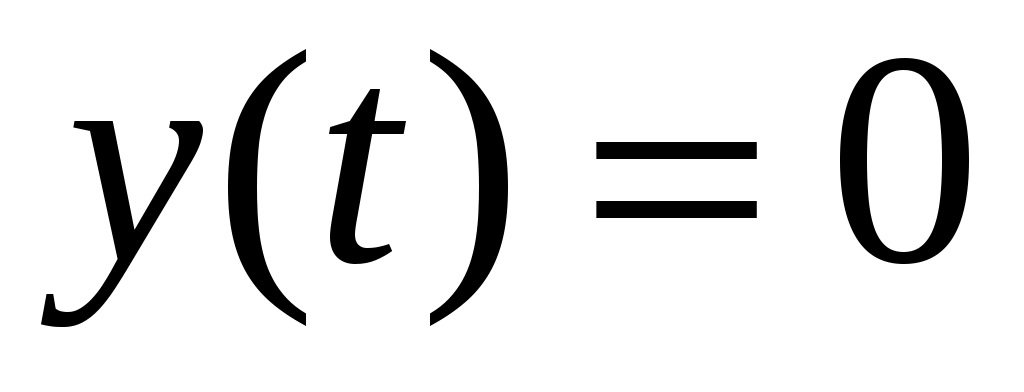 . Следовательно, подставляя исходные данные в выражение (1), получим: . Следовательно, подставляя исходные данные в выражение (1), получим:
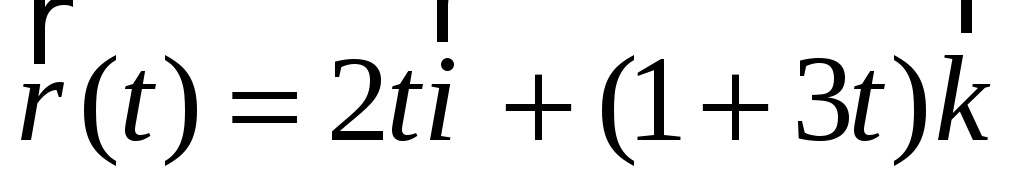 . .
Полученный в данном задании результат будет под цифрой 3.
Задание 2.
Если радиус-вектор частицы изменяется со временем по закону 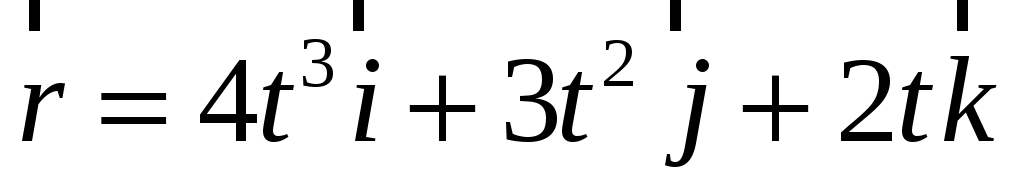 (м), то для момента времени две секунды модуль скорости частицы будет равен (м), то для момента времени две секунды модуль скорости частицы будет равен
|
1) 50 м/с;
|
2) 60 м/с;
|
3) 70 м/с;
|
4) 80 м/с.
|
Дано:
|
Решение:
|
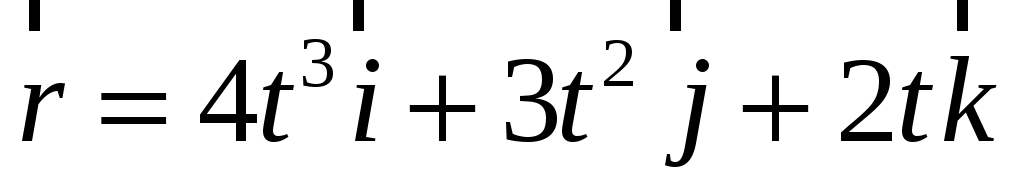 (м) (м)
|
В соответствии с выражением (1.8) ортогональное разложение вектора скорости имеет вид:
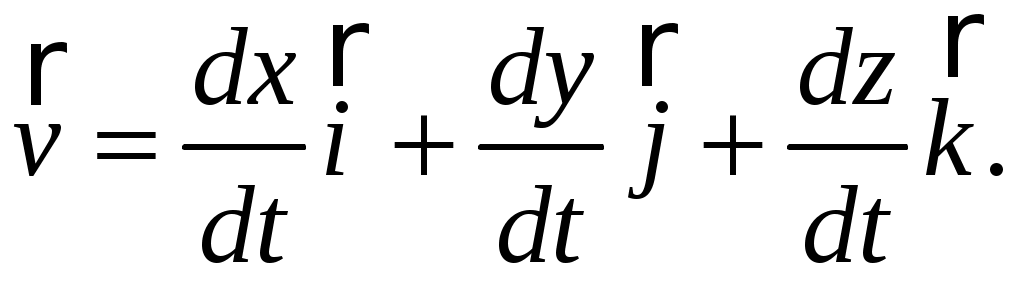
|
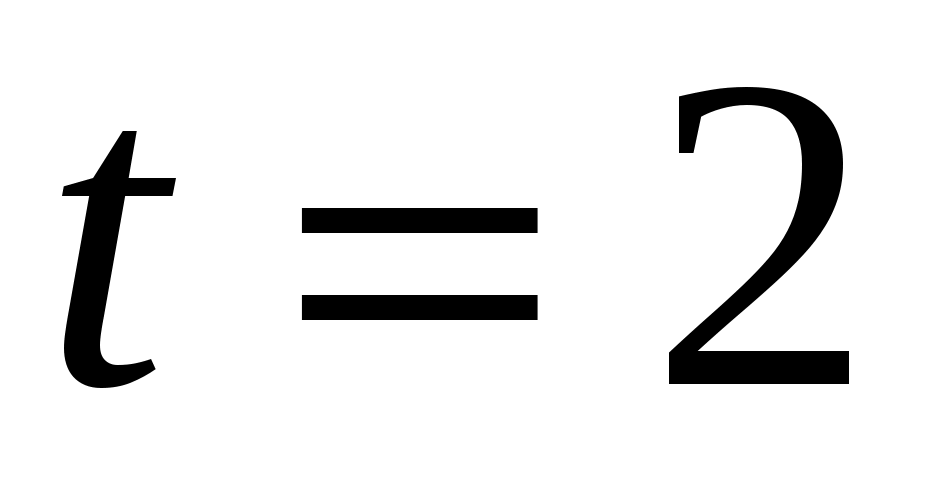 с с
|
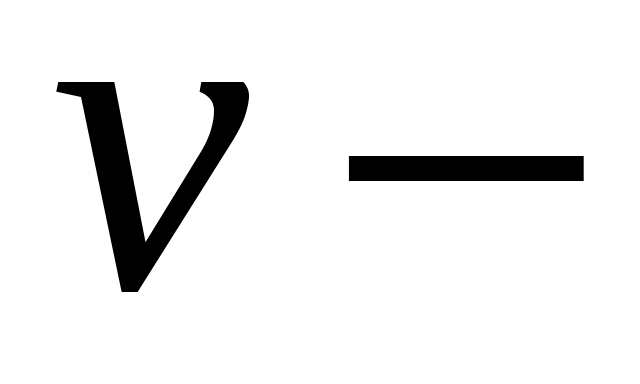 ? ?
|
Сравнивая исходное выражение 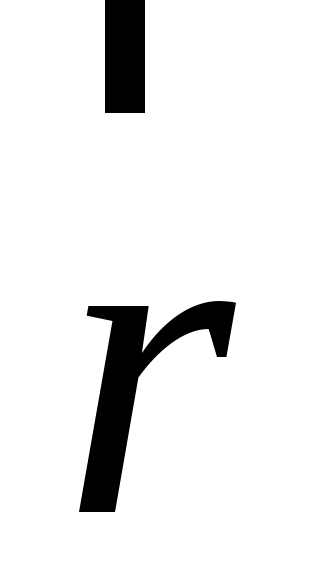 с его ортогональным разложением (1.1), запишем с его ортогональным разложением (1.1), запишем
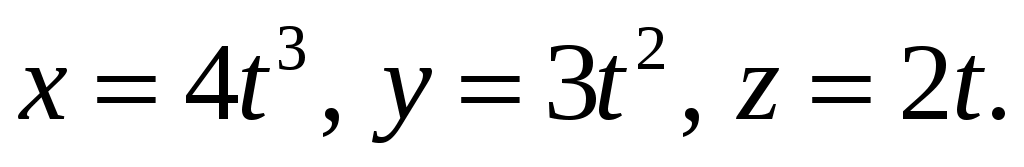
С учетом этого получим
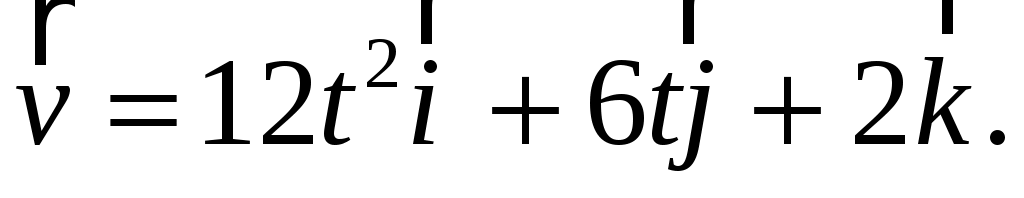
Модуль вектора 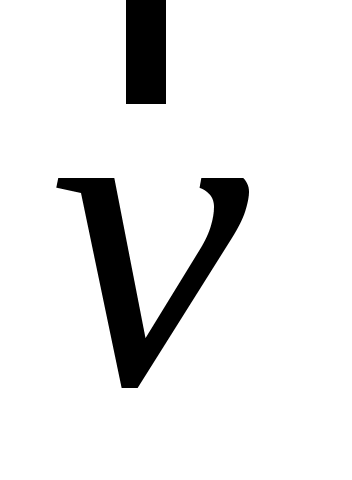 в соответствии с выражением (1.9) имеет вид в соответствии с выражением (1.9) имеет вид
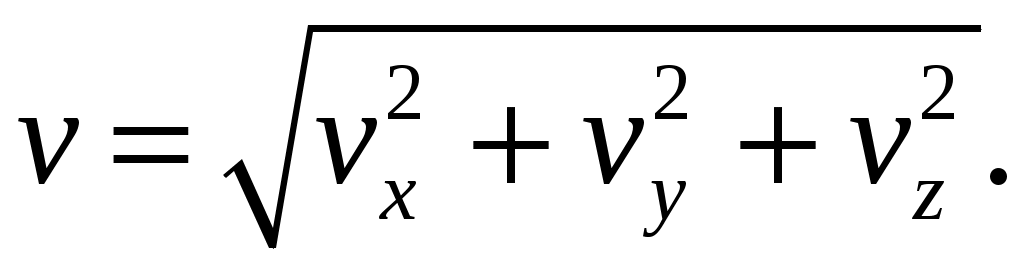
Следовательно, искомая величина:
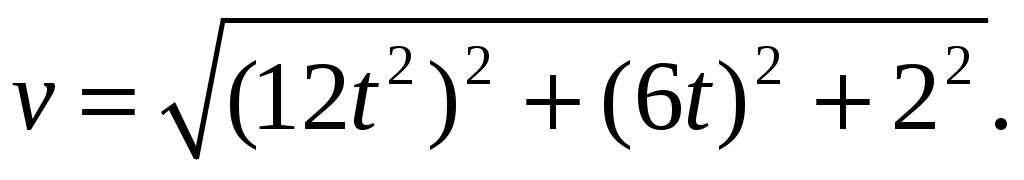
Подставим значение времени 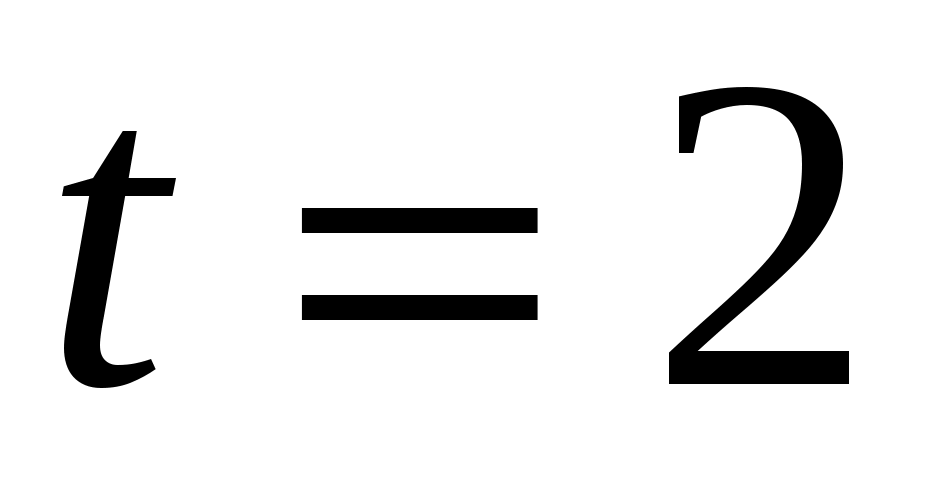 с: с:
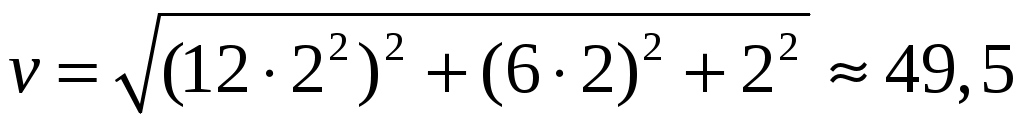 (м/с). (м/с).
Полученный в данном задании результат наиболее близок к ответу под цифрой 1.
Задание 3.
Если координаты частицы заданы в виде 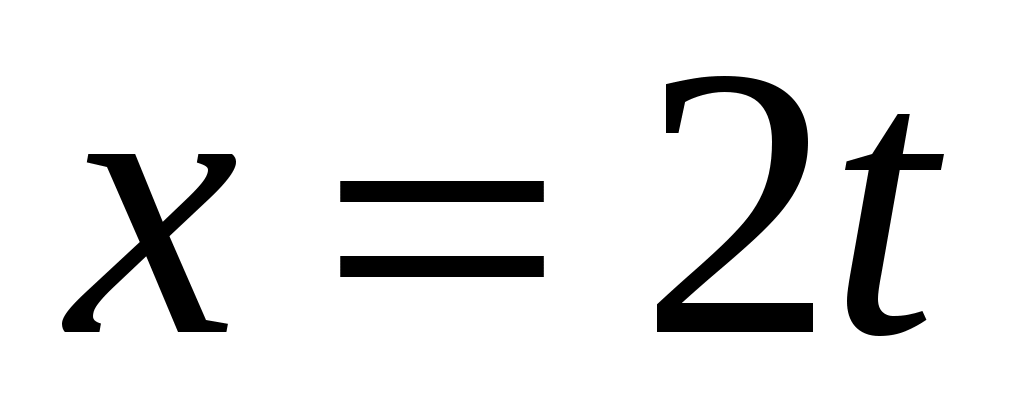 (м); (м); 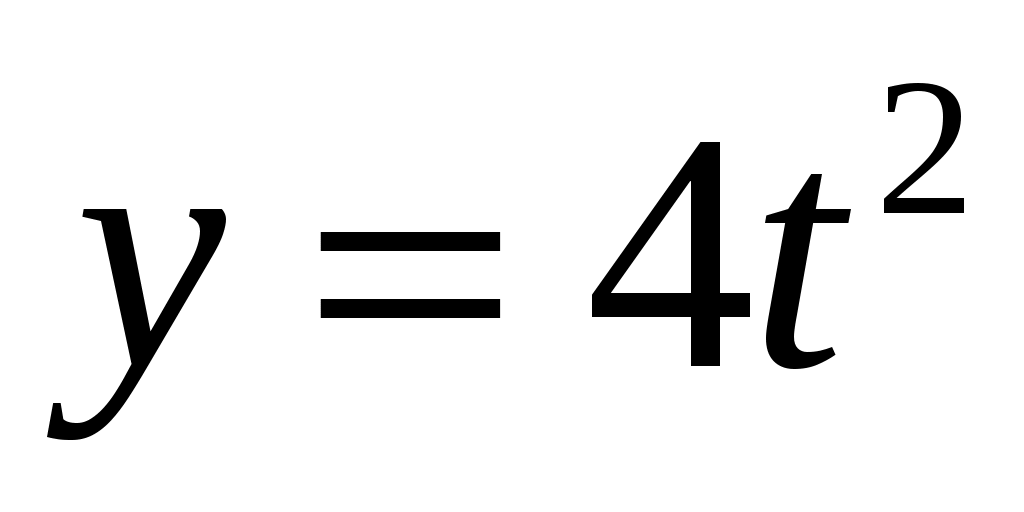 (м); (м); 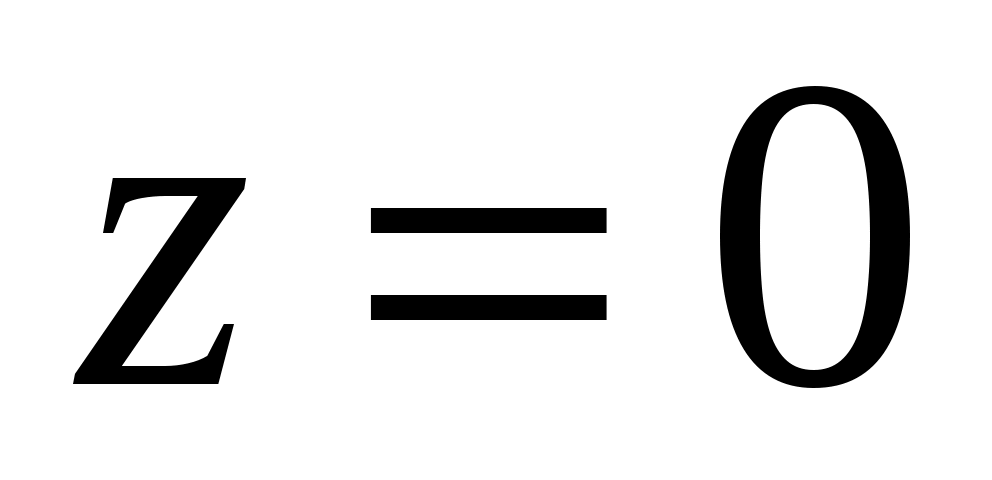 , то форма траектории частицы будет иметь вид , то форма траектории частицы будет иметь вид
|
1) прямой линии;
|
2) окружности;
|
3) эллипса;
|
4) параболы.
|
Дано:
|
Решение:
|
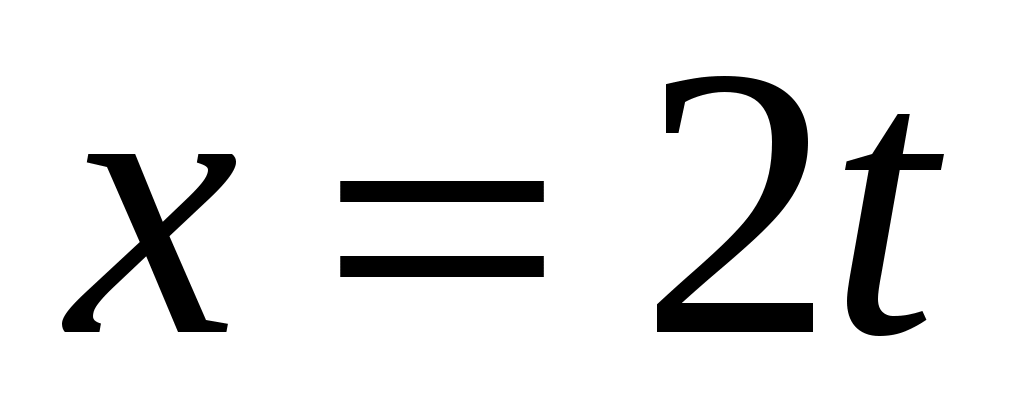 (м) (м)
|
Поскольку 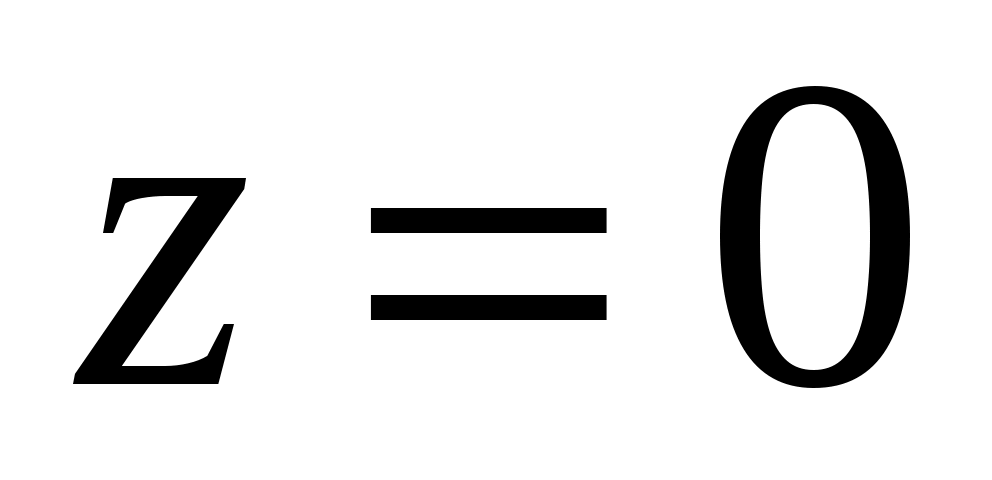 , то траектория частицы будет лежать в плоскости , то траектория частицы будет лежать в плоскости 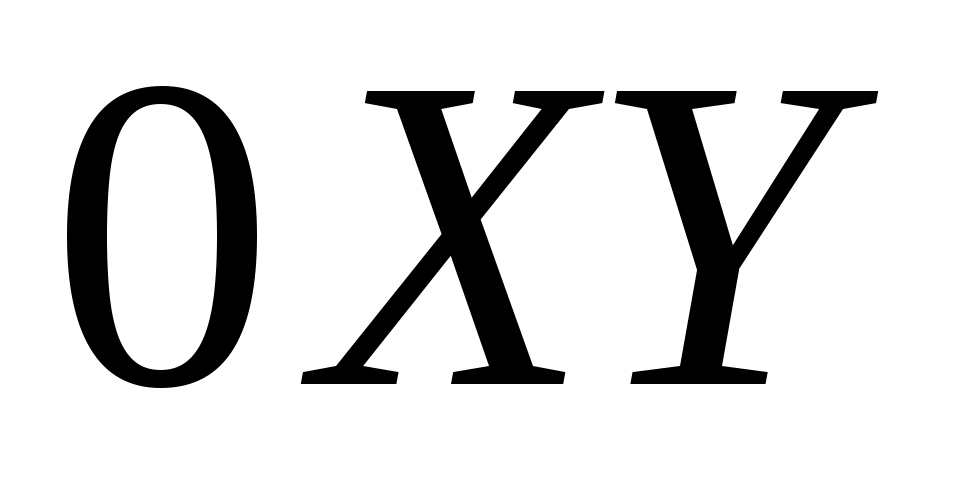 и будет иметь вид и будет иметь вид 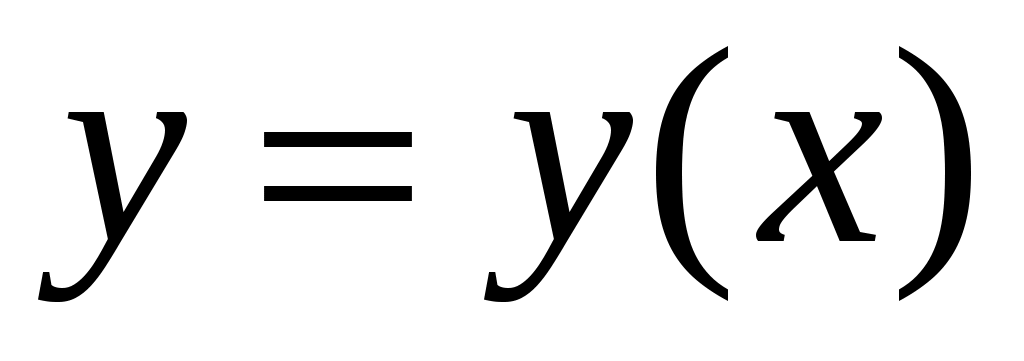 . Из исходного выражения координаты . Из исходного выражения координаты 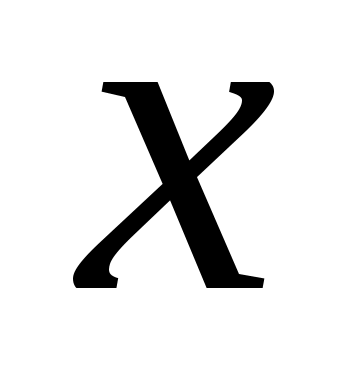 выразим время: выразим время:
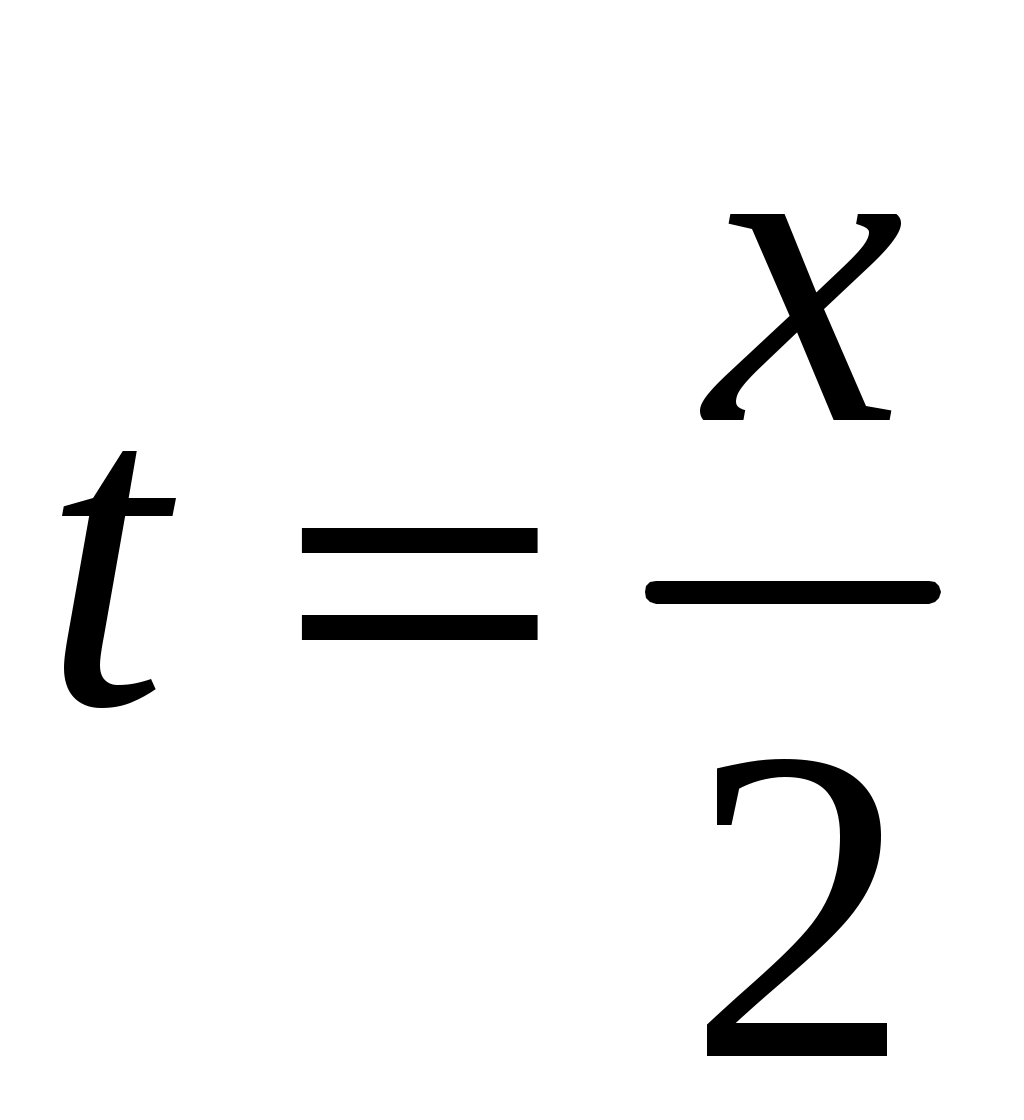
|
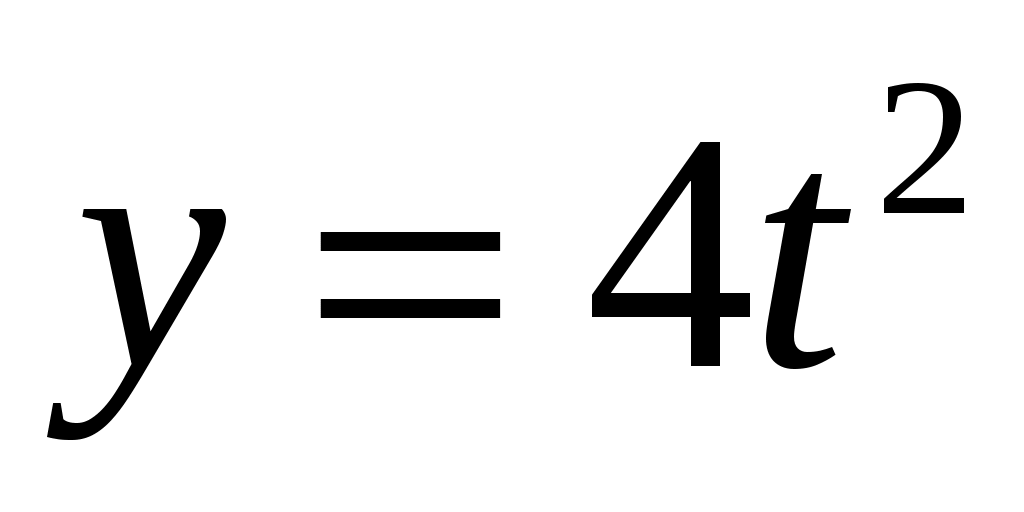 (м) (м)
|
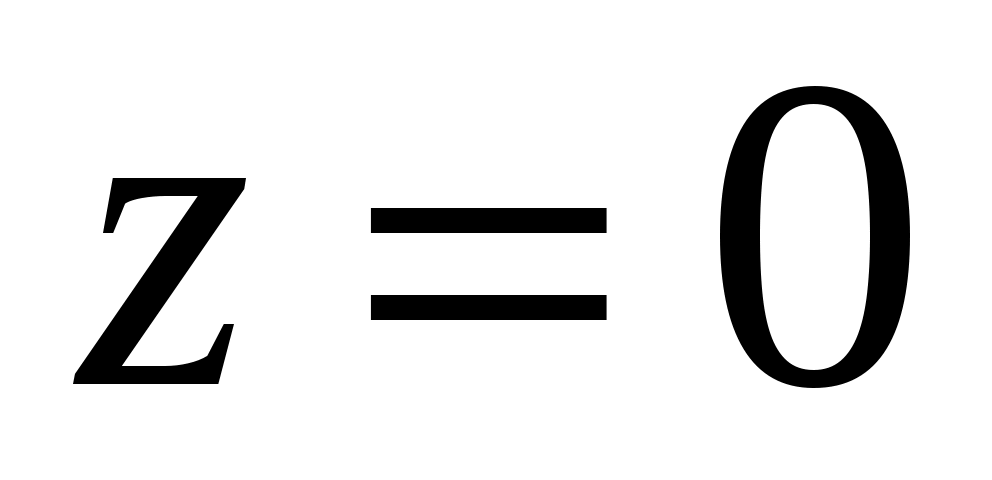
|
 ? ?
|
и подставим его в исходное выражение координаты 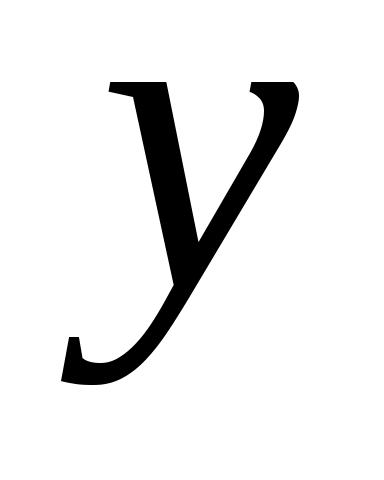 : :
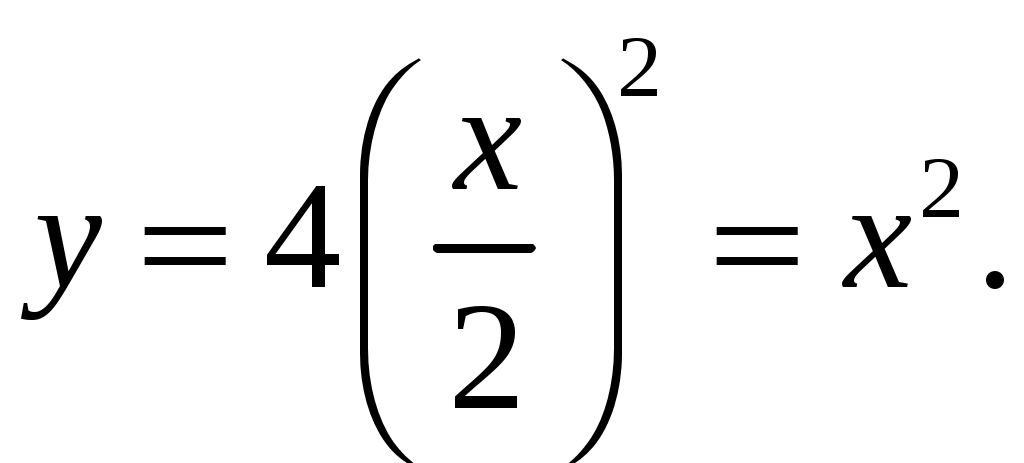
Полученный в данном задании результат выражает собой уравнение параболы, т.е. правильный ответ будет под цифрой 4.
Задание 4.
Если координата частицы задана уравнением 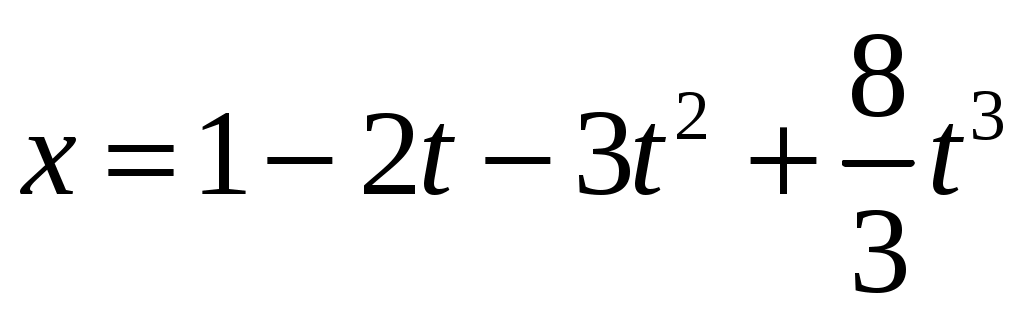 (м), то путь, пройденный частицей за две секунды от начала ее движения, будет равен (м), то путь, пройденный частицей за две секунды от начала ее движения, будет равен
|
1) 5 м;
|
2) 10 м;
|
3) 15 м;
|
4) 20 м.
|
Дано:
|
Решение:
|
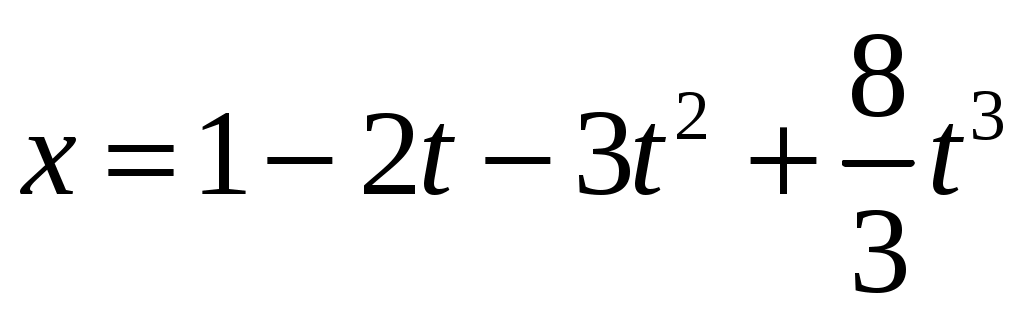 (м) (м)
|
Вначале проверим, не имела ли частица разворота на интервале наблюдения от 0 до 2 с в соответствии с условием (1.12):
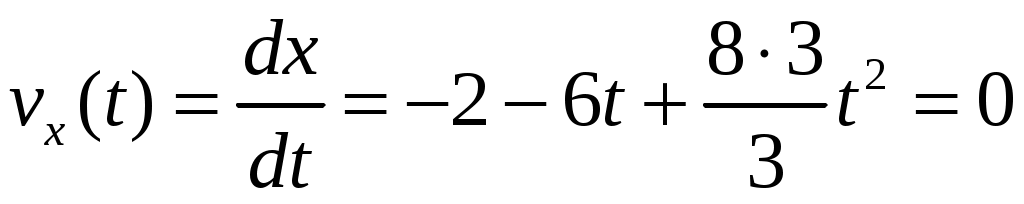
|
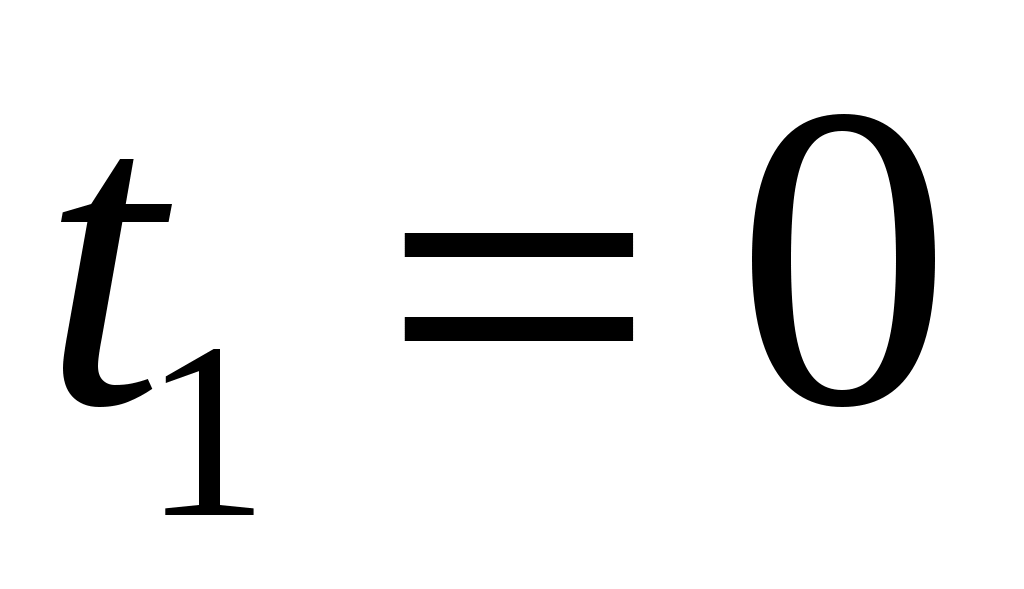 с с
|
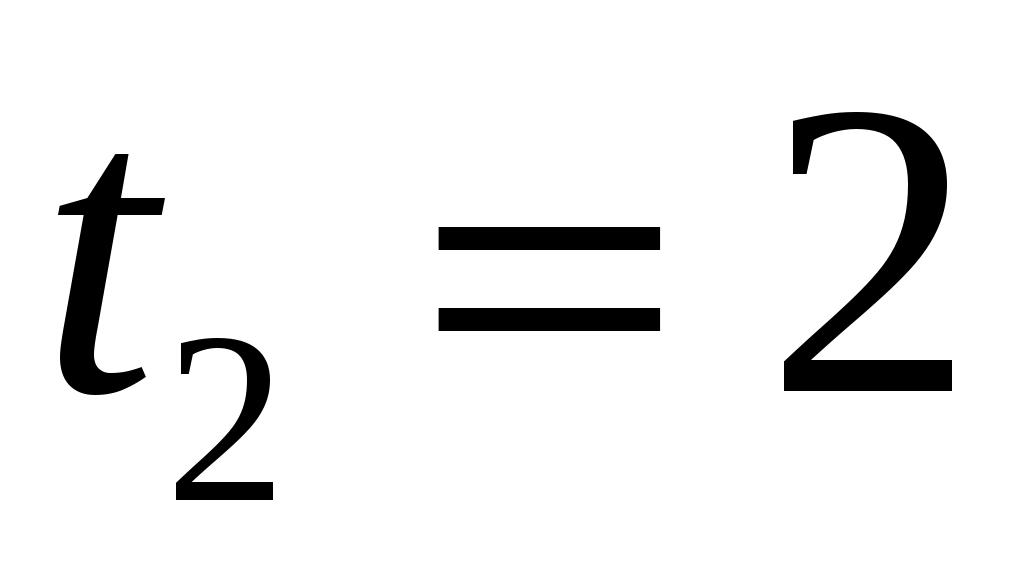 с с
|
 ? ?
|
или
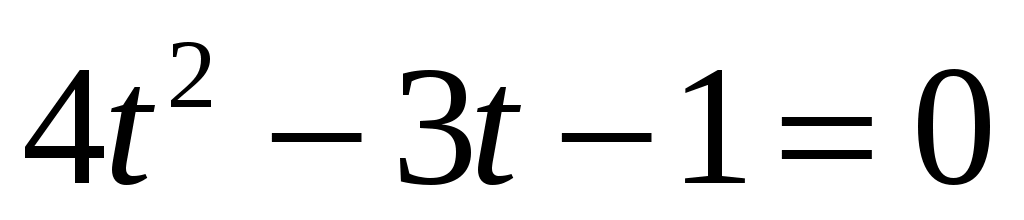 , ,
откуда дискриминант уравнения
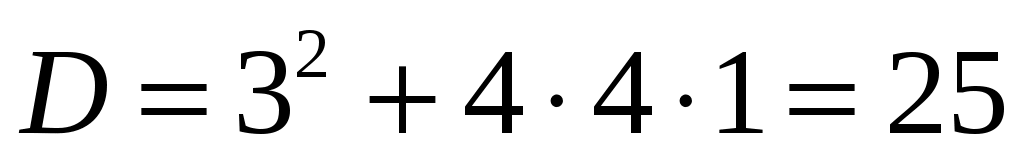 . .
Тогда
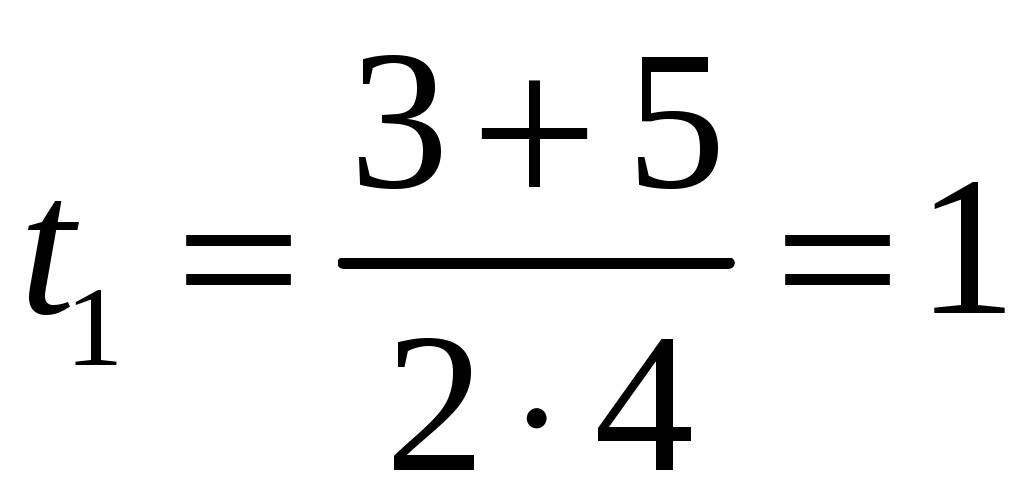 (с); (с); 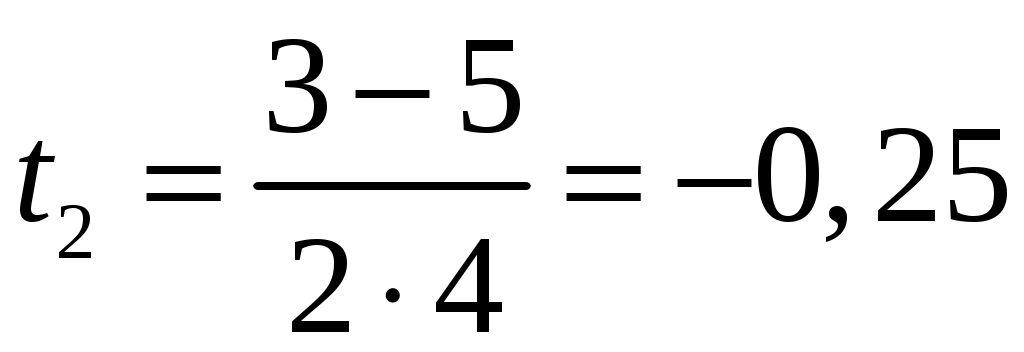 (с). (с).
Следовательно, разворот был, т.к. время разворота 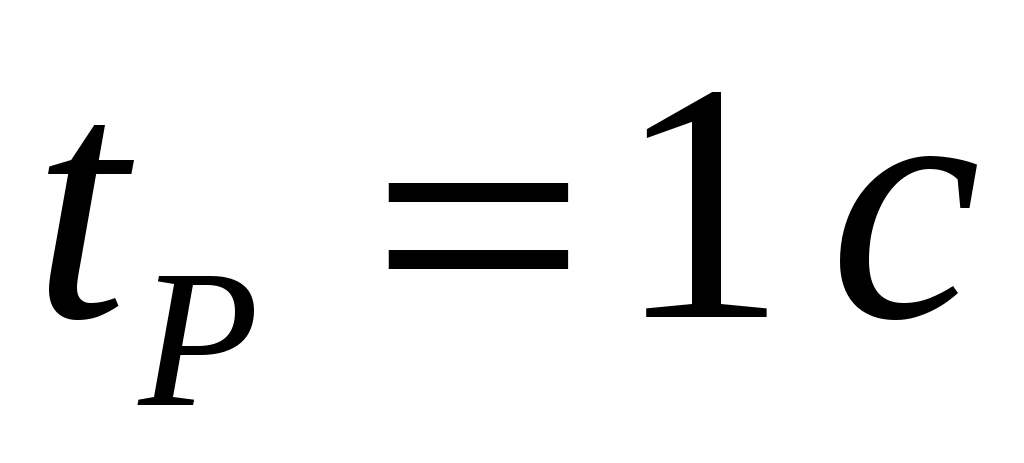 принадлежит интервалу наблюдения в данном задании от 0 до 2 секунд. По этой причине общий путь принадлежит интервалу наблюдения в данном задании от 0 до 2 секунд. По этой причине общий путь 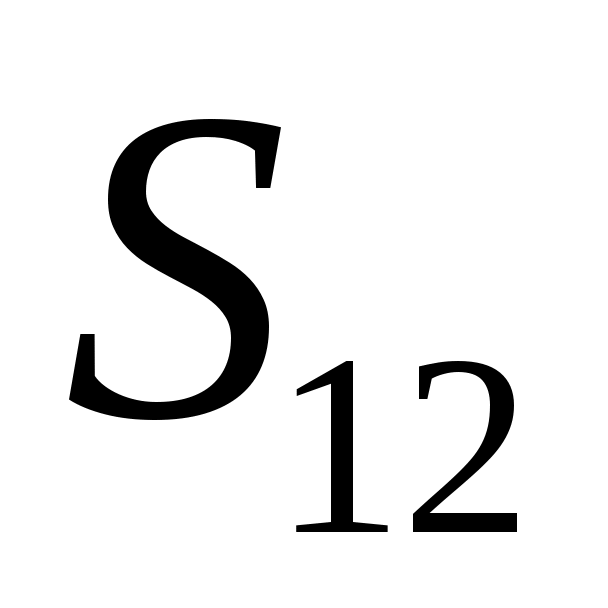 будет равен сумме путей: будет равен сумме путей:
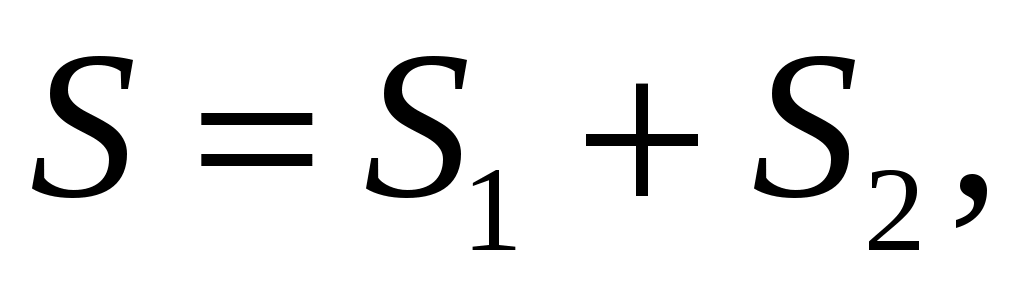
где 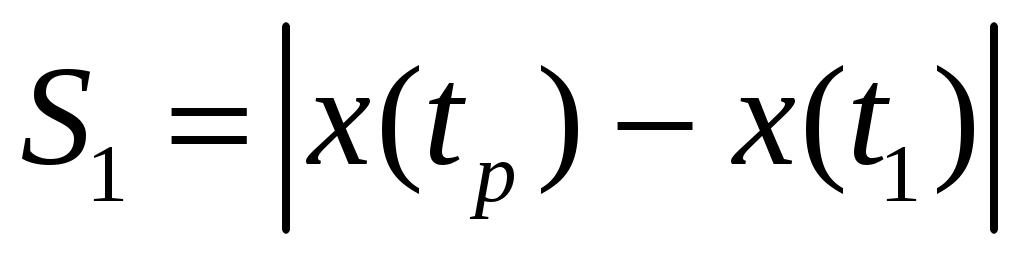 – путь частицы от момента времени – путь частицы от момента времени 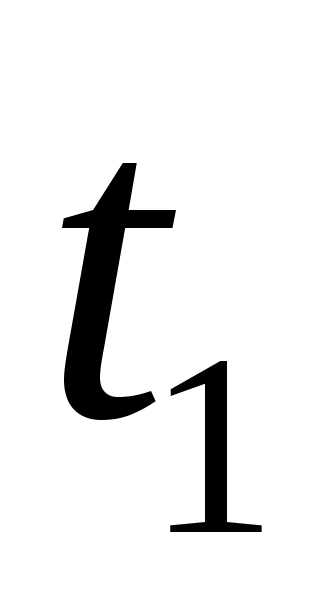 до разворота; до разворота;
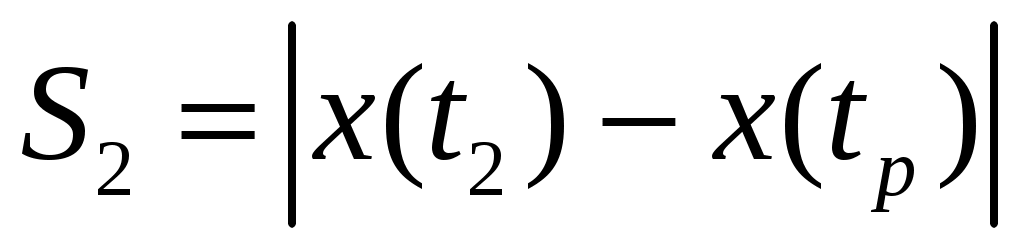 – путь частицы от разворота до момента времени – путь частицы от разворота до момента времени 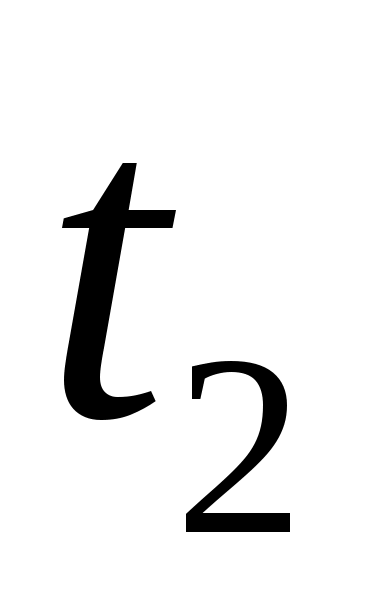 . .
Путь до разворота
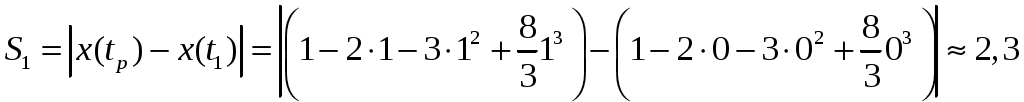 (м). (м).
Путь после разворота
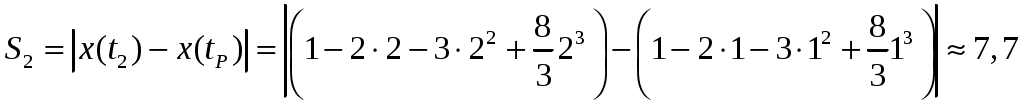 (м). (м).
Суммарный путь
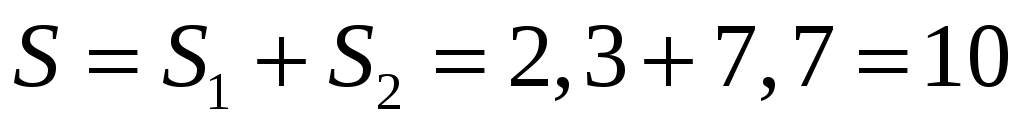 (м). (м).
Полученный в данном задании результат будет под цифрой 2.
Задание 5.
Если координата частицы задана уравнением 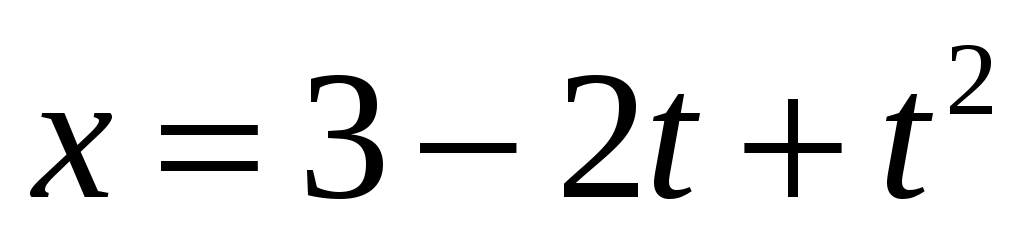 (м), то средняя скорость частицы за третью секунду ее движения будет равна (м), то средняя скорость частицы за третью секунду ее движения будет равна
|
1) 3 м/с;
|
2) 4 м/с;
|
3) 5 м/с;
|
4) 6 м/с.
|
Дано:
|
Решение:
|
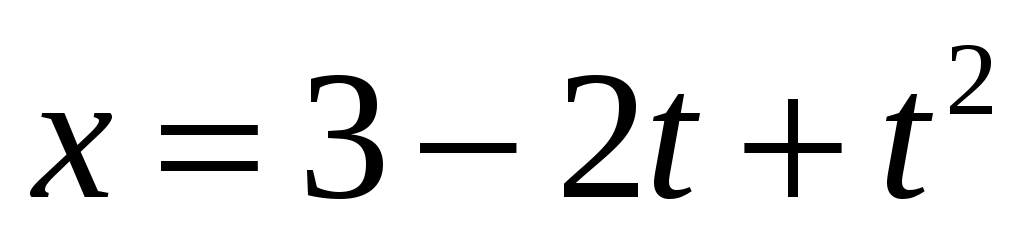 (м) (м)
|
По определению (1.14), средняя скорость:
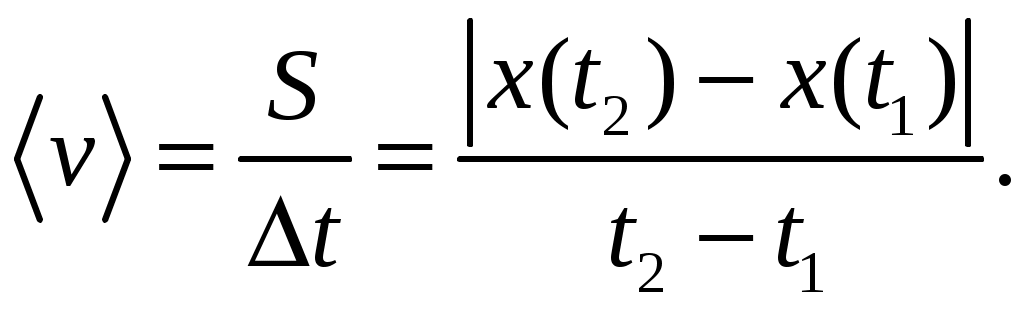
|
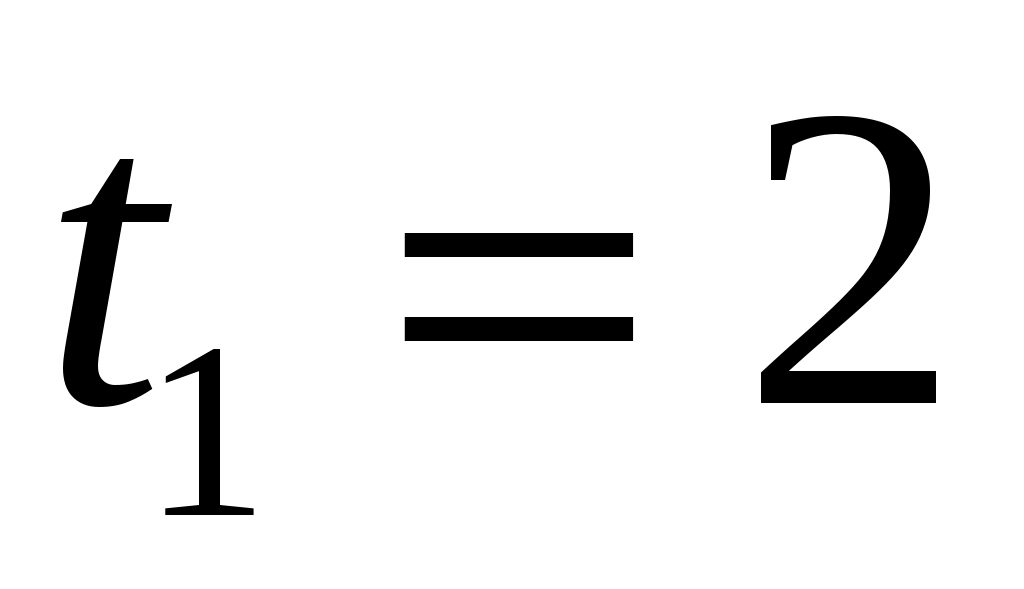 с с
|
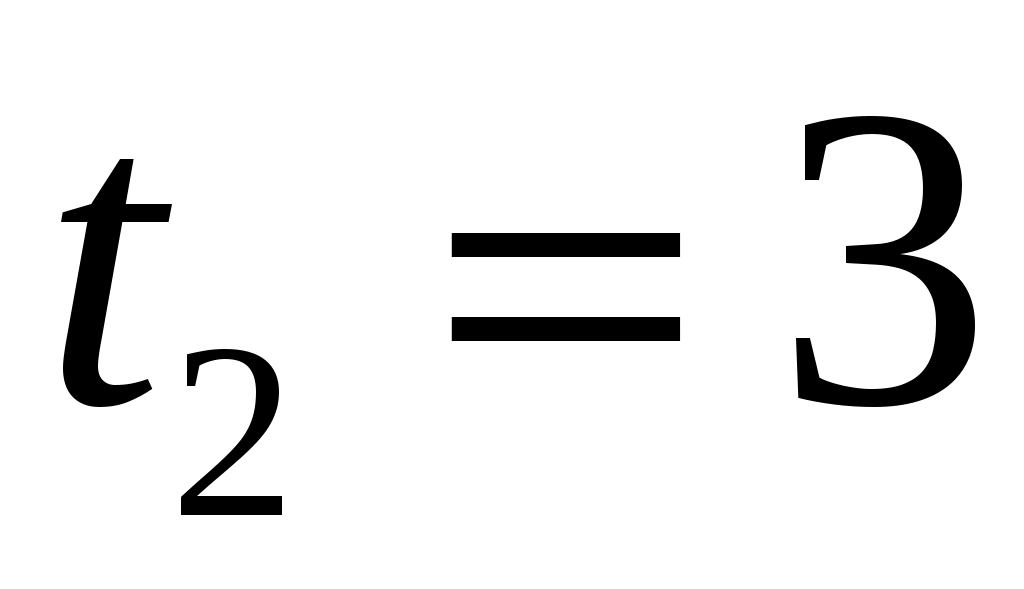 с с
|
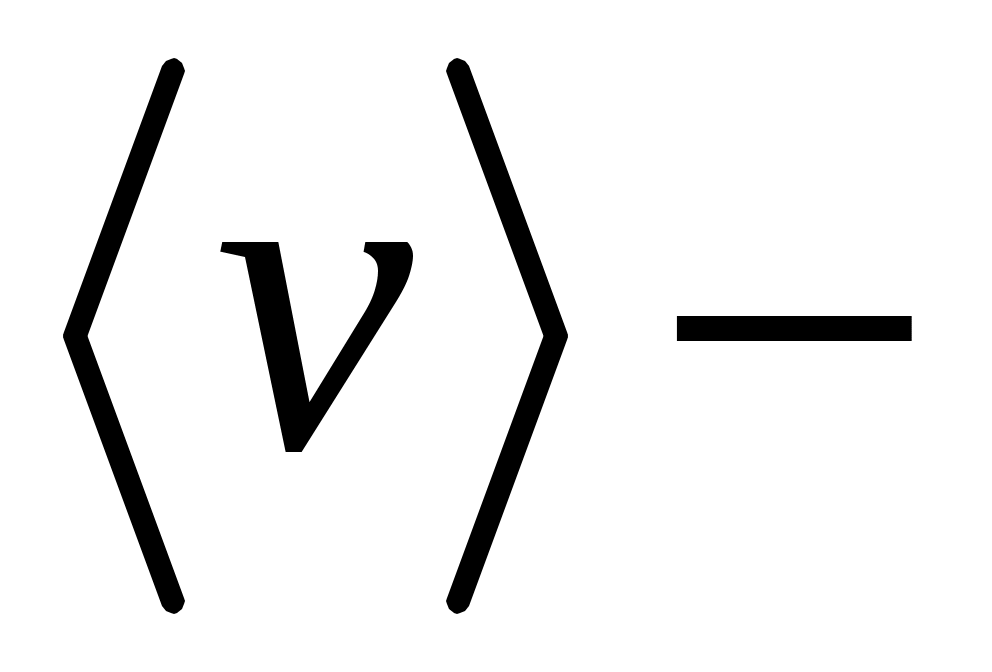 ? ?
|
Следовательно
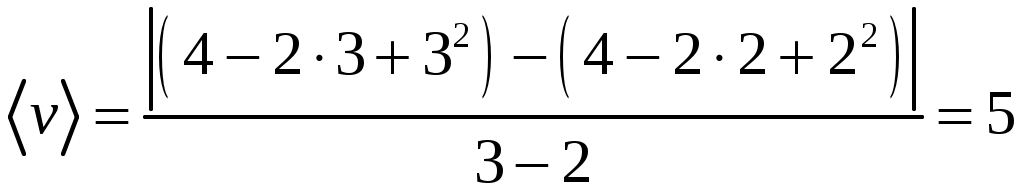 (м/с). (м/с).
Полученный в данном задании результат будет под цифрой 3.
Задание 6.
Координата частицы задана уравнением 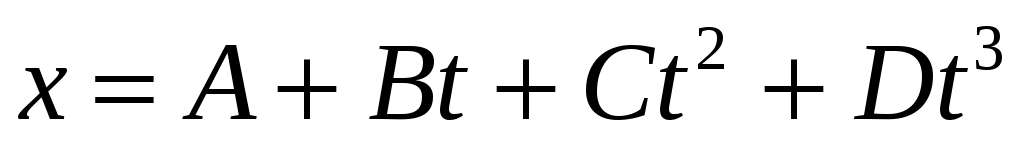 . Если С = 0,5 м/с2; D = 1 м/с3, то время после начала движения частицы, когда она будет иметь ускорение 7 м/с2, будет равно . Если С = 0,5 м/с2; D = 1 м/с3, то время после начала движения частицы, когда она будет иметь ускорение 7 м/с2, будет равно
|
1) 1 с;
|
2) 2 с;
|
3) 3 с;
|
4) 4 с.
|
Дано:
|
Решение:
|
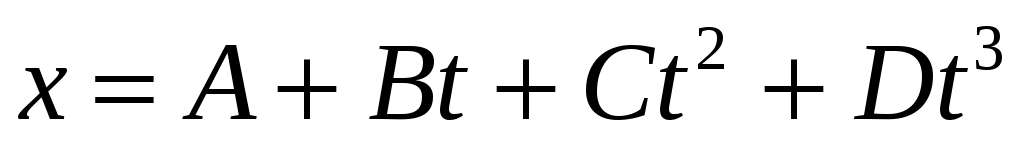
|
По определению (1.14), проекция ускорения на ось  : :
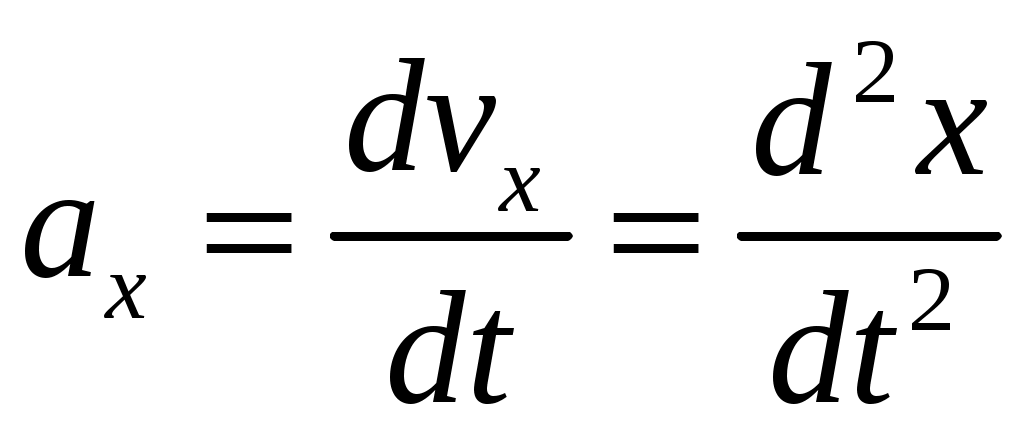 . .
Скорость определим в соответствии с выражением (1.8):
|
С = 0,5 м/с2
|
D = 1 м/с3
|
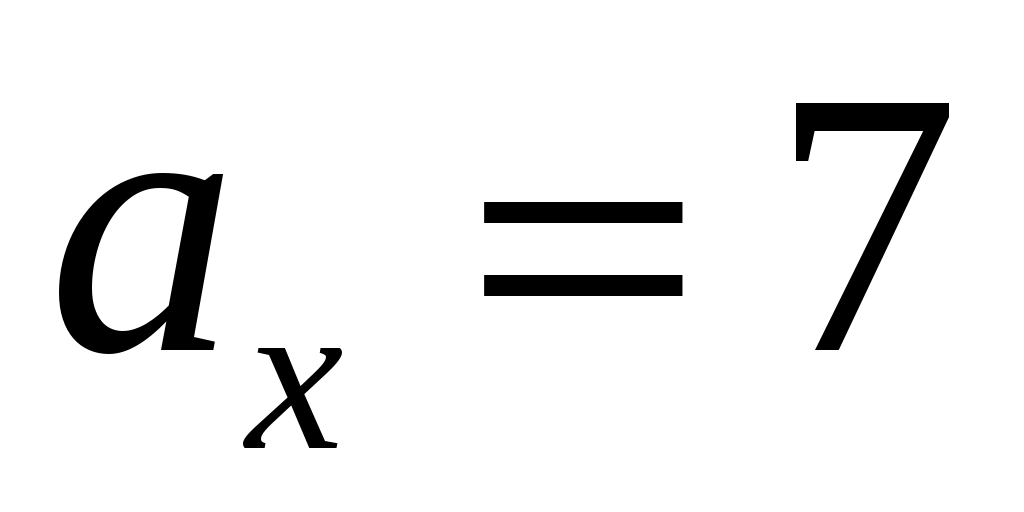 м/с2 м/с2
|
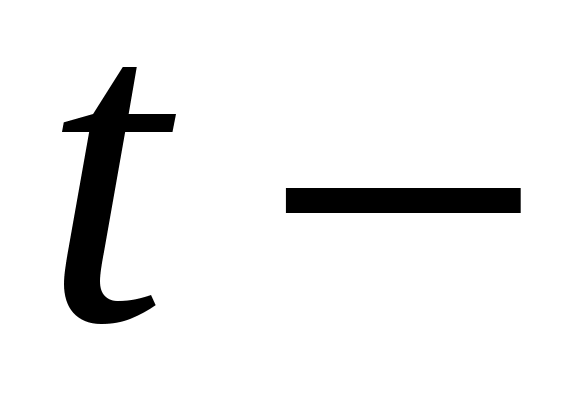 ? ?
|
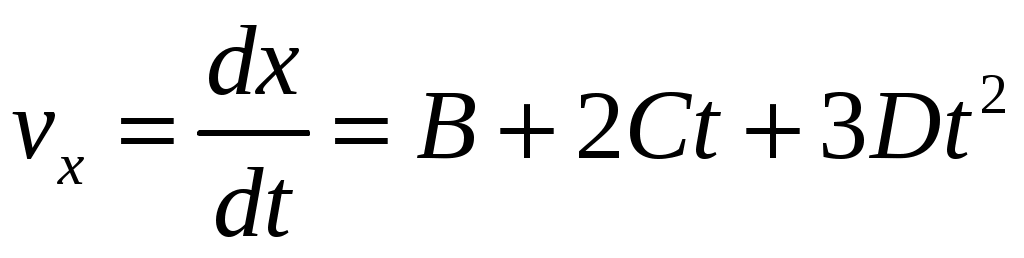 . .
Следовательно ускорение
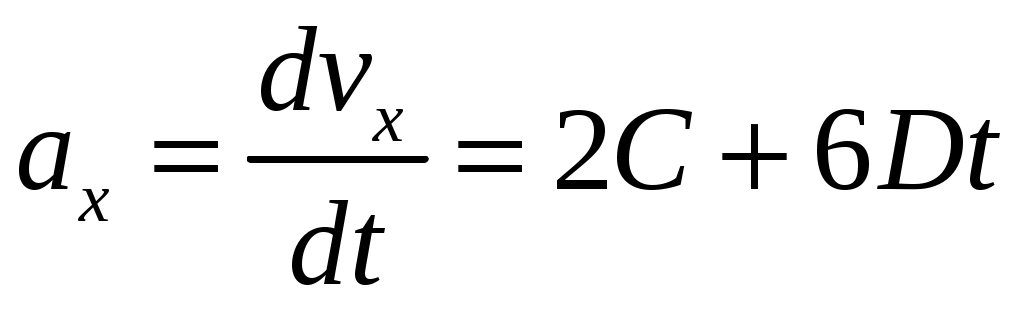 . .
По условию 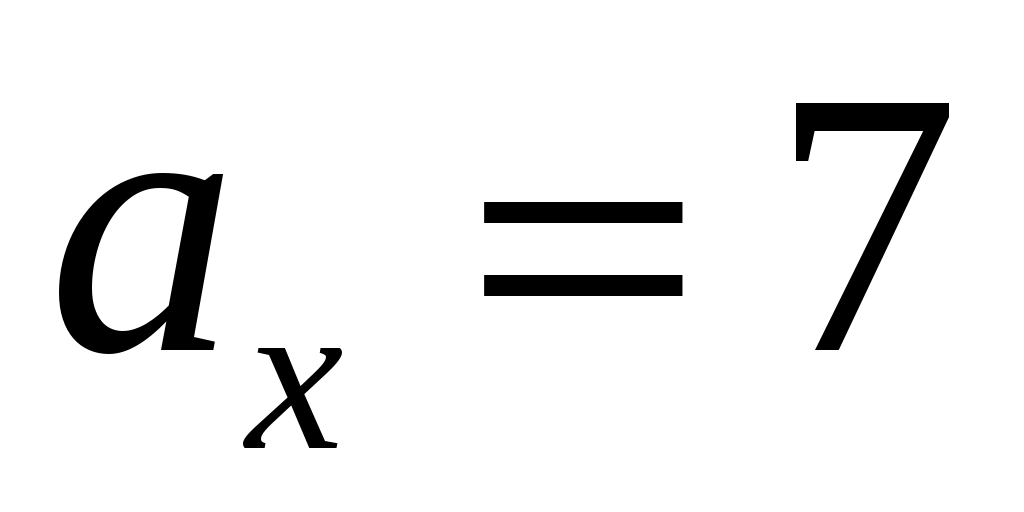 м/с2, т.е. м/с2, т.е.
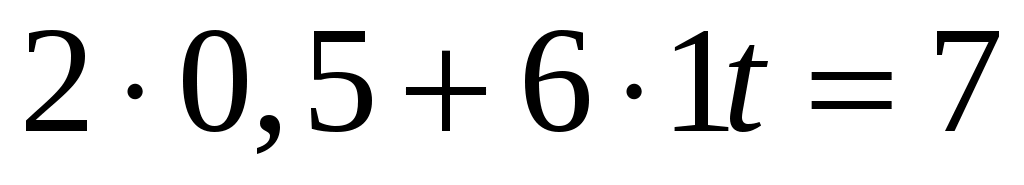 , ,
откуда
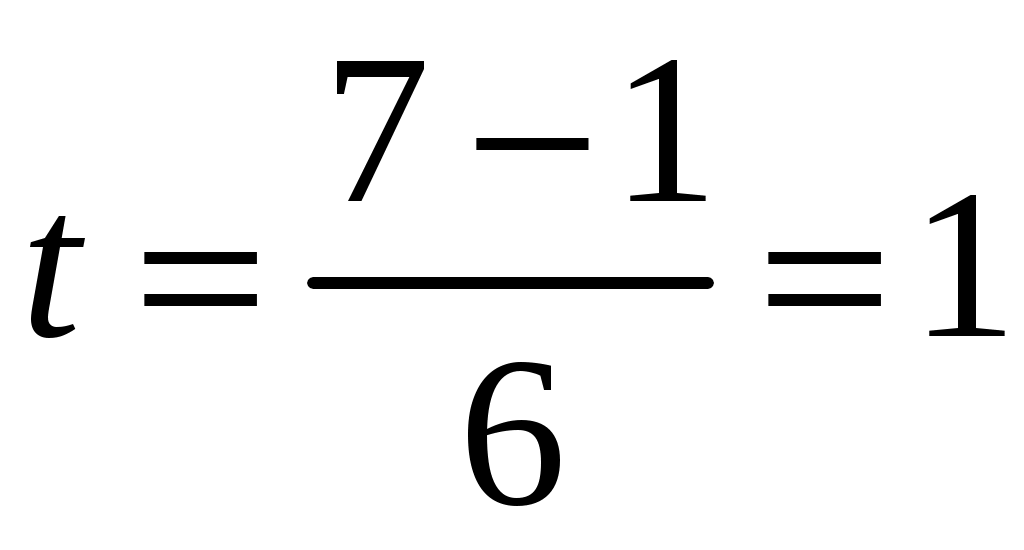 (с). (с).
Полученный в данном задании результат будет под цифрой 1.
Задание 7.
Если координата частицы задана уравнением 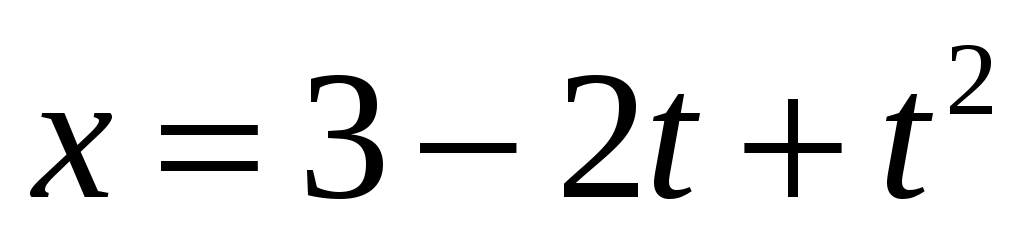 (м), то среднее ускорение частицы за первые три секунды ее движения будет равно (м), то среднее ускорение частицы за первые три секунды ее движения будет равно
|
1) 2 м/с2;
|
2) 4 м/с2;
|
3) 6 м/с2;
|
4) 8 м/с2.
|
Дано:
|
Решение:
|
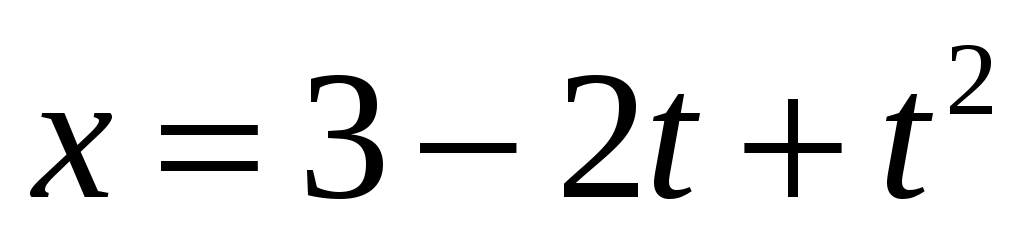 (м) (м)
|
По определению (1.17), среднее ускорение:
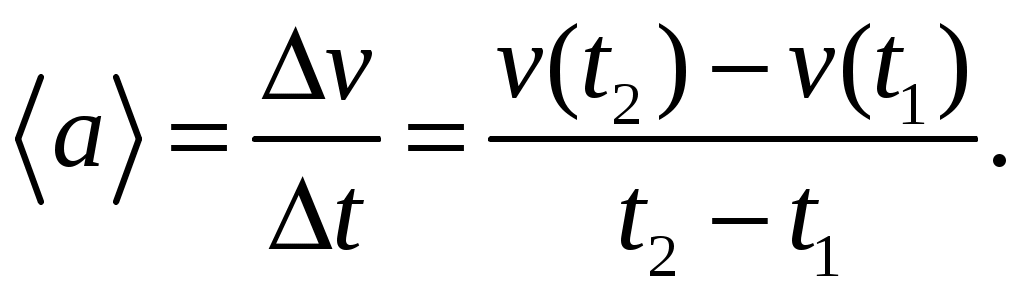
Скорость определим в соответствии с выражением (1.8):
|
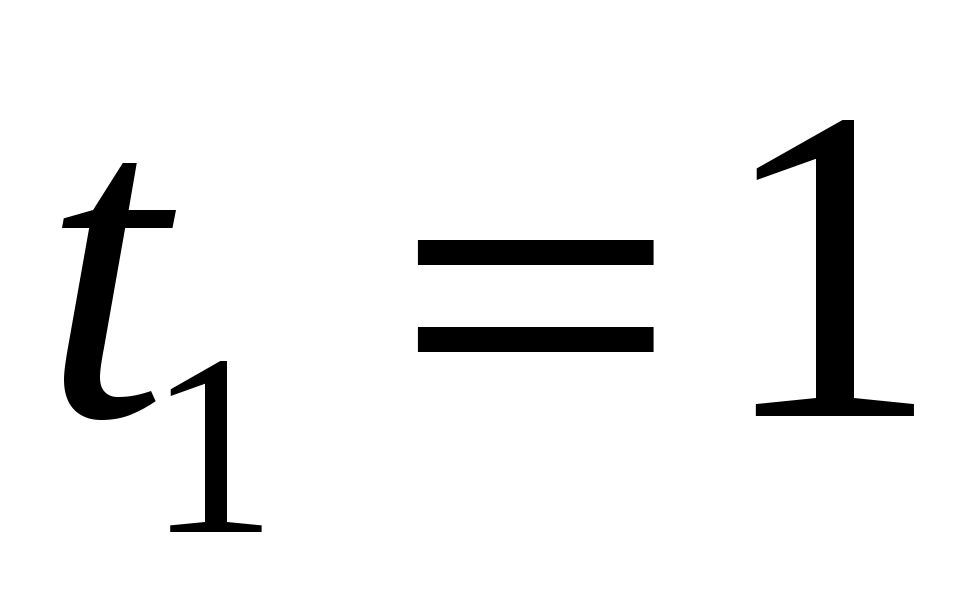 с с
|
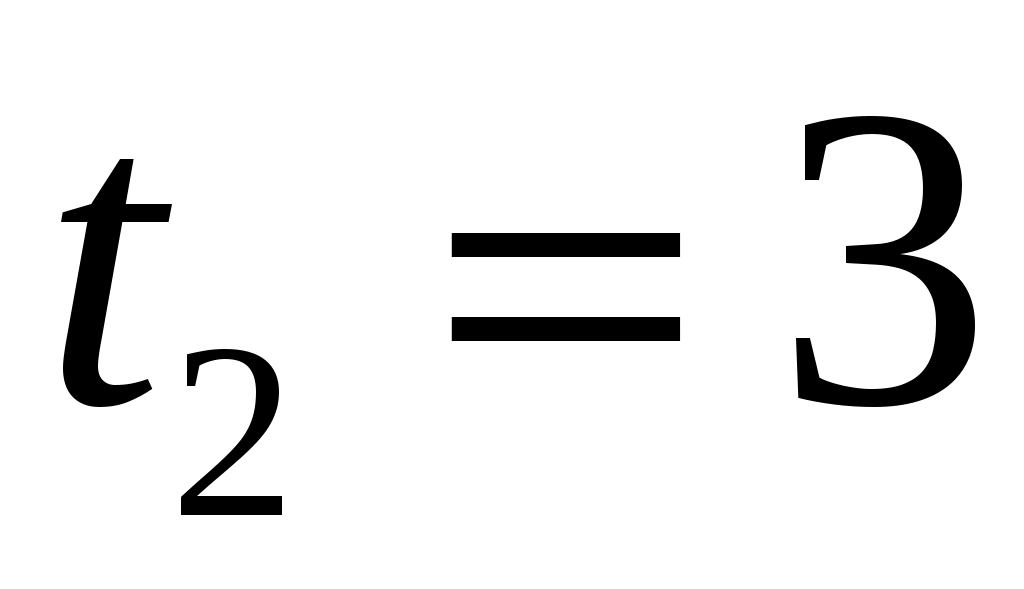 с с
|
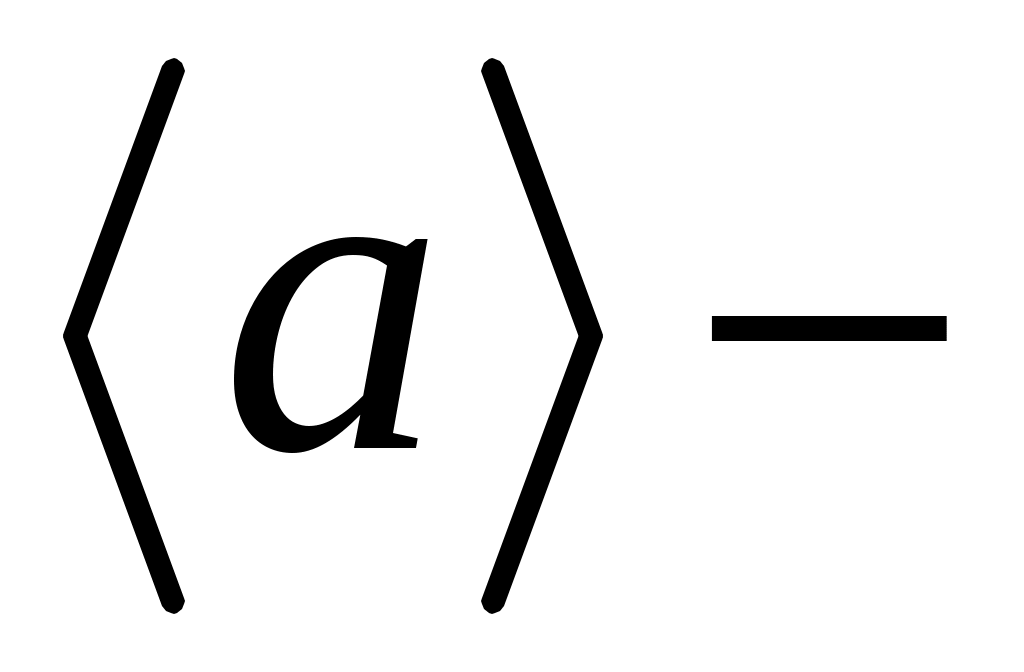 ? ?
|
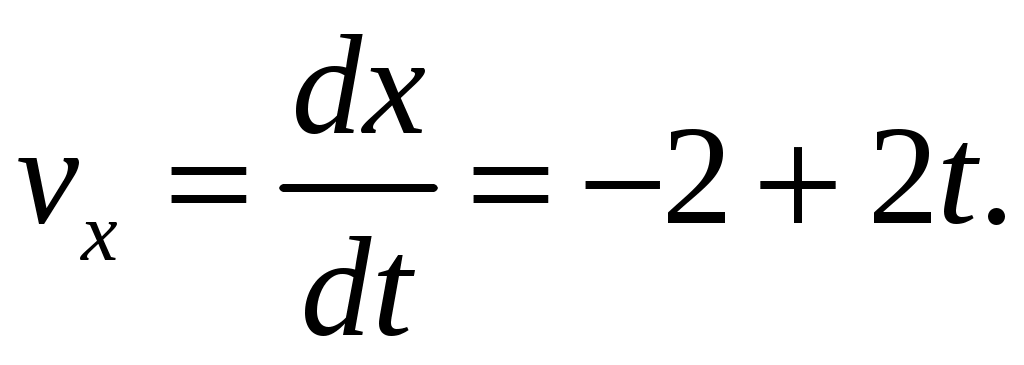
Следовательно, среднее ускорение за указанное в задании время:
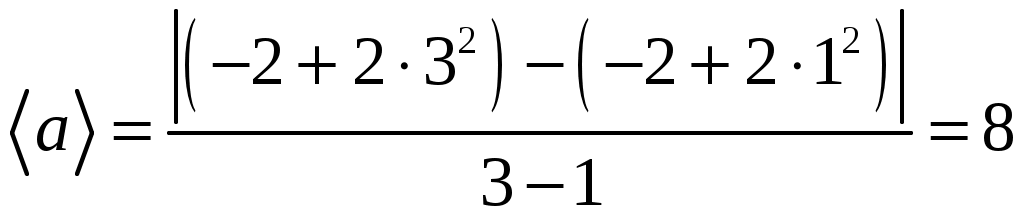 (м/с2). (м/с2).
Полученный в данном задании результат будет под цифрой 4.
Кинематика вращательного движения
Задание 8.
Если диск вращается вокруг неподвижной оси так, что его угловая координата определяется уравнением 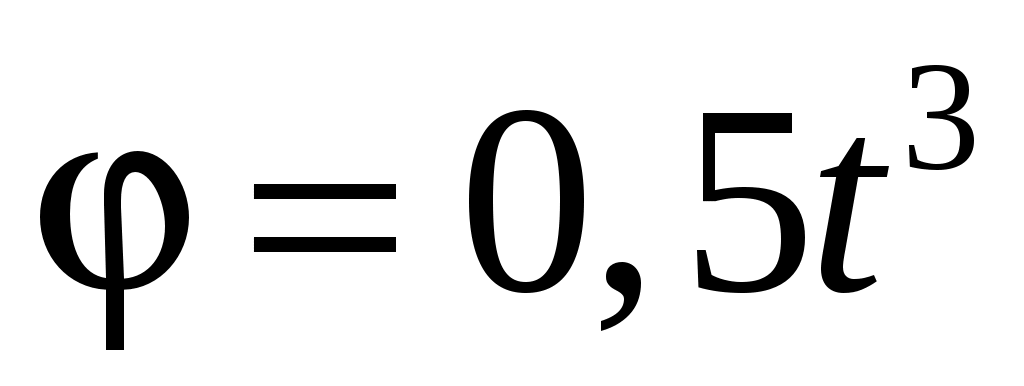 (рад), то его угловое ускорение через две секунды от начала движения будет равно (рад), то его угловое ускорение через две секунды от начала движения будет равно
|
1) 5 рад/с2;
|
2) 6 рад/с2;
|
3) 7 рад/с2;
|
4) 8 рад/с2.
|
Дано:
|
Решение:
|
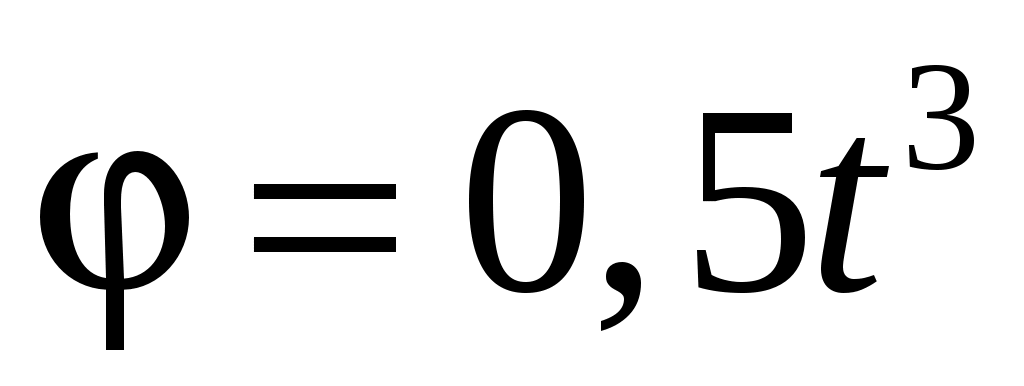 (рад) (рад)
|
По определению (1.20), модуль углового ускорения:
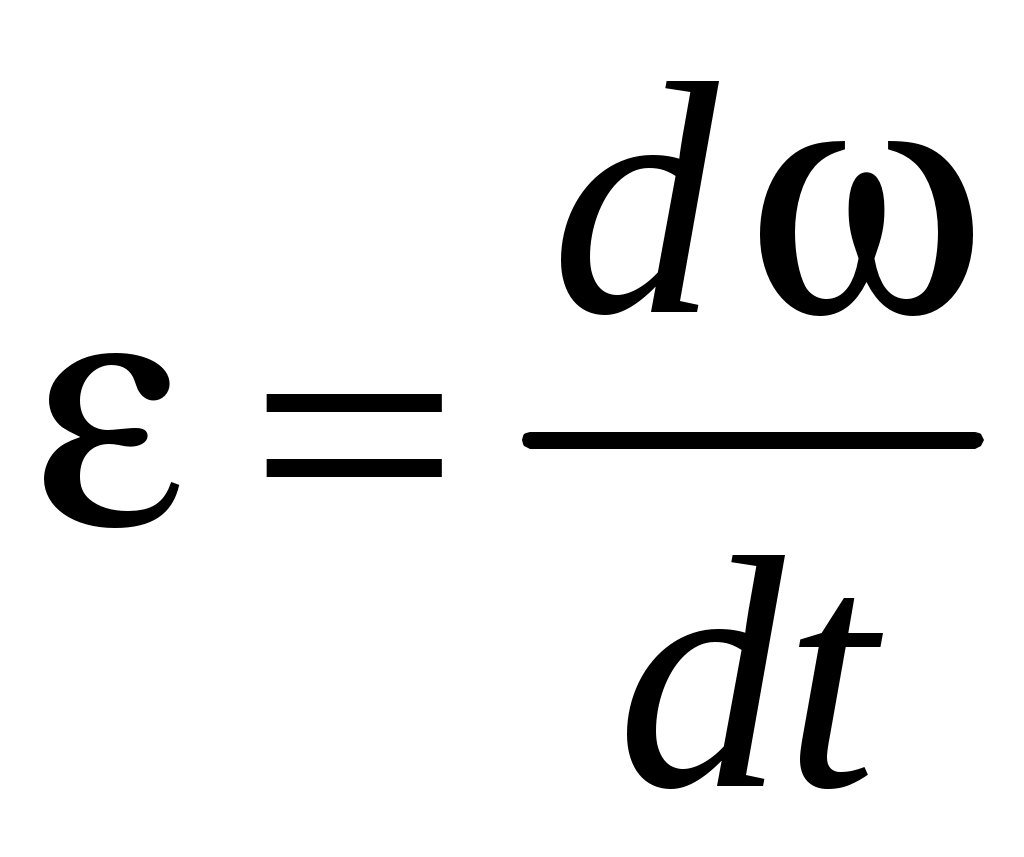 . .
|
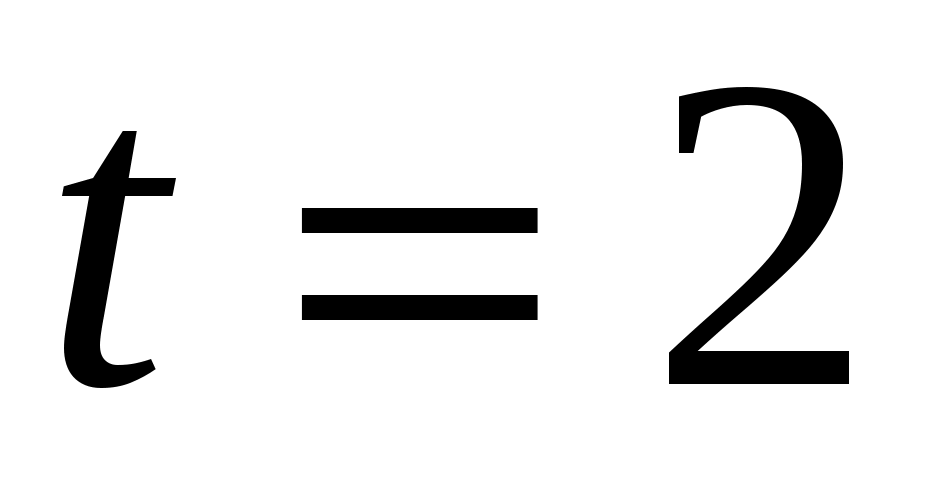 с с
|
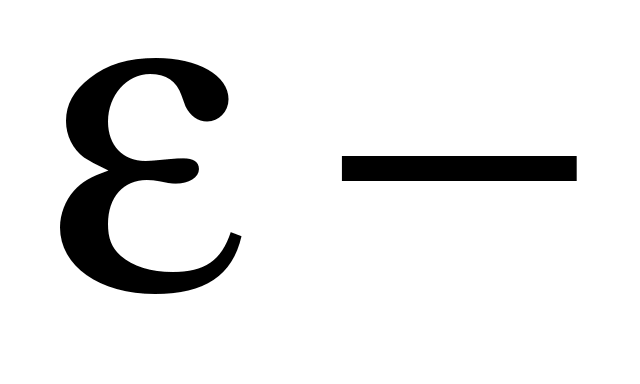 ? ?
|
Определим модуль угловой скорости по исходному выражению угловой координаты с учетом выражения (1.18):
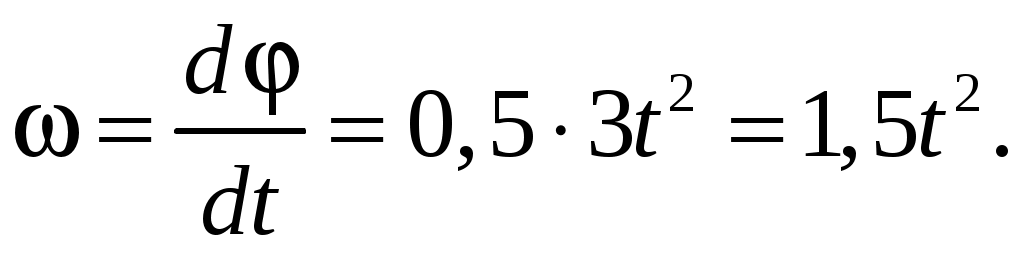
Тогда искомая величина примет вид:
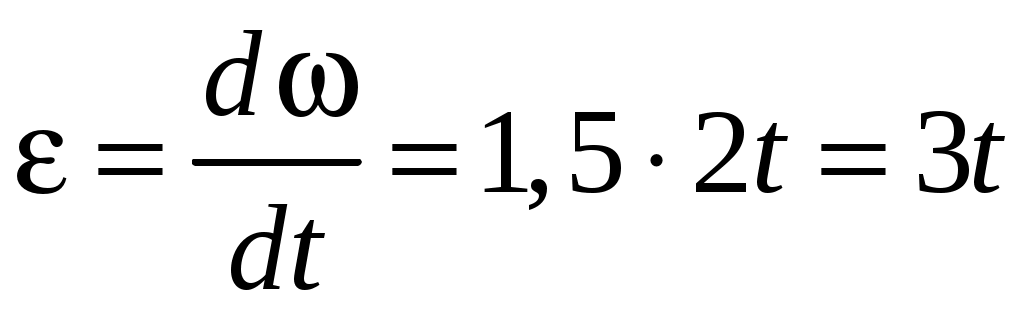 . .
Вычислим значение искомой величины:
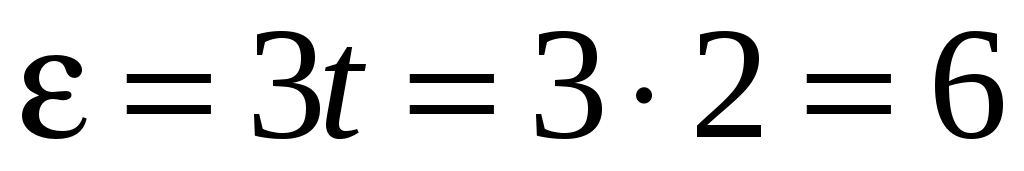 (рад/с2). (рад/с2).
Полученный в данном задании результат будет под цифрой 2.
Задание 9.
Если колесо радиусом 0,6 м вращается так, что его угловая координата задана уравнением 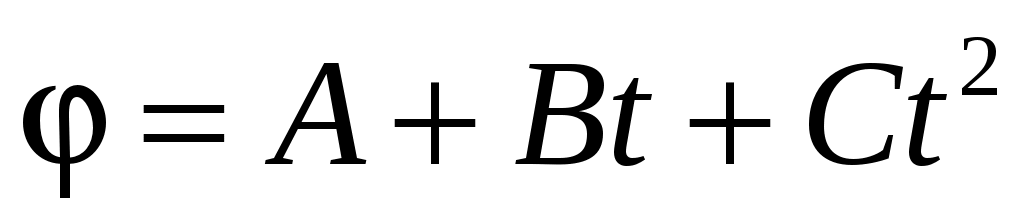 , где С = 3 рад/с2, то касательное ускорение точек на ободе колеса будет равно , где С = 3 рад/с2, то касательное ускорение точек на ободе колеса будет равно
|
1) 1,6 м/с2;
|
2) 2,6 м/с2;
|
3) 3,6 м/с2;
|
4) 4,6 м/с2.
|
Дано:
|
Решение:
|
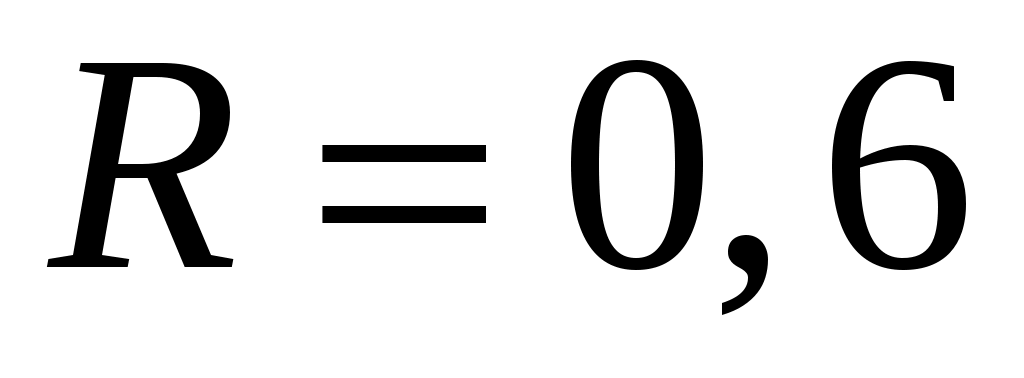 м м
|
По определению (1.23), модуль касательного ускорения:
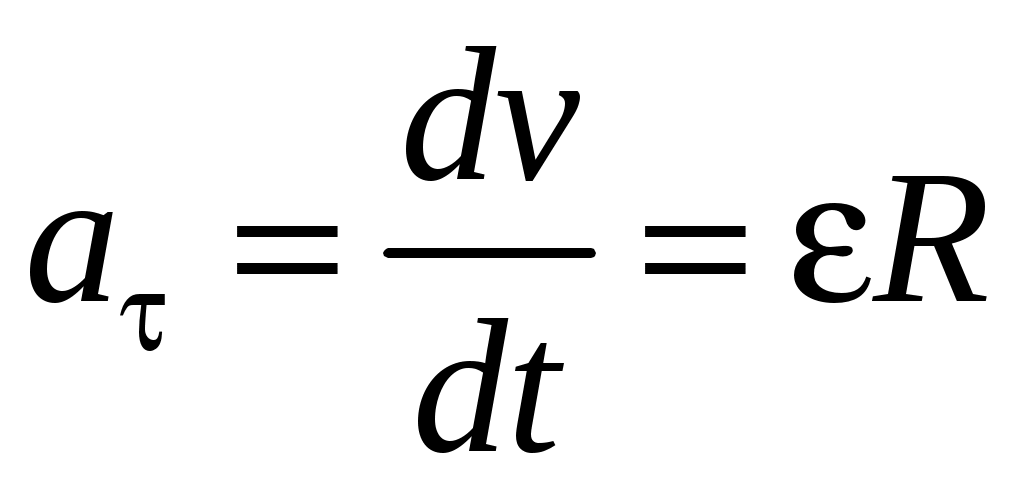 . .
С учетом выражений (1.18)и (1.20) имеем:
|
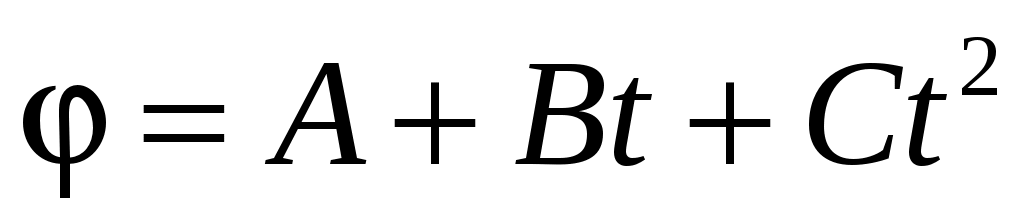
|
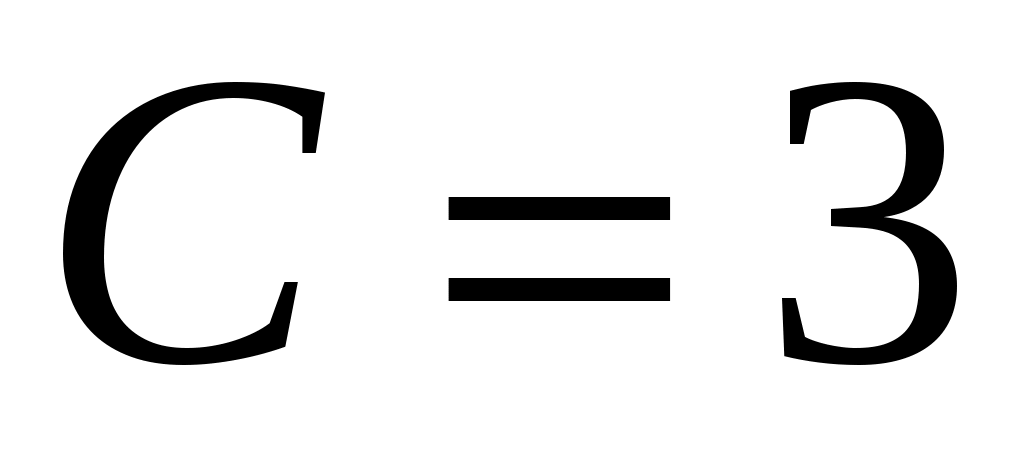 рад/с2 рад/с2
|
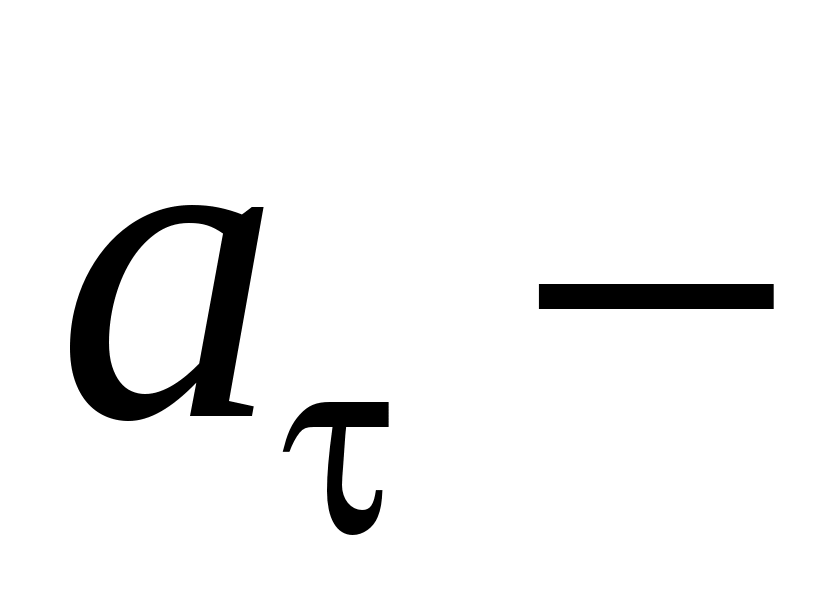 ? ?
|
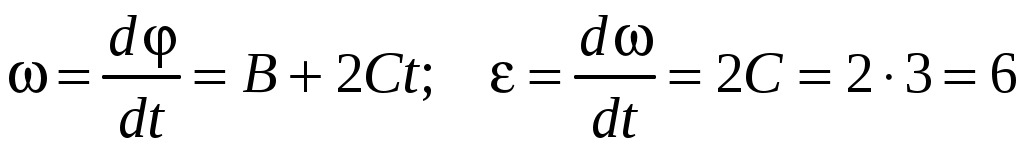 (рад/с2). (рад/с2).
Обратим внимание на то, что в данном задании угловое ускорение не зависит от времени. Следовательно, искомая величина:
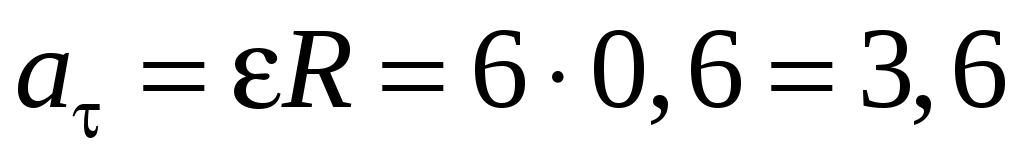 (м/с2). (м/с2).
Полученный в данном задании результат будет под цифрой 3.
Задание 10.
Если колесо радиусом 10 см вращается так, что линейная скорость точек на его ободе задана уравнением 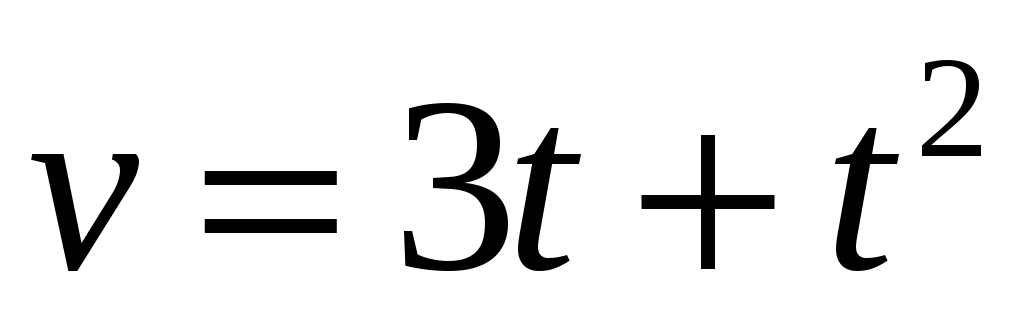 (см/с), то спустя одну секунду после начала движения угол между вектором полного ускорения и радиусом колеса будет равен (см/с), то спустя одну секунду после начала движения угол между вектором полного ускорения и радиусом колеса будет равен
|
1) 30о;
|
2) 45о;
|
3) 60о;
|
4) 70о.
|
Дано:
|
СИ
|
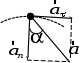
|
Решение:
|
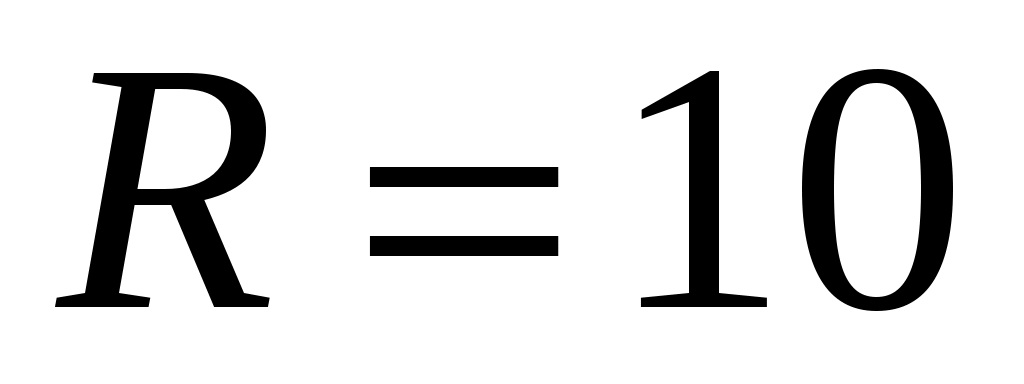 см см
|
0,1 м
|
Искомый угол определим через его тангенс:
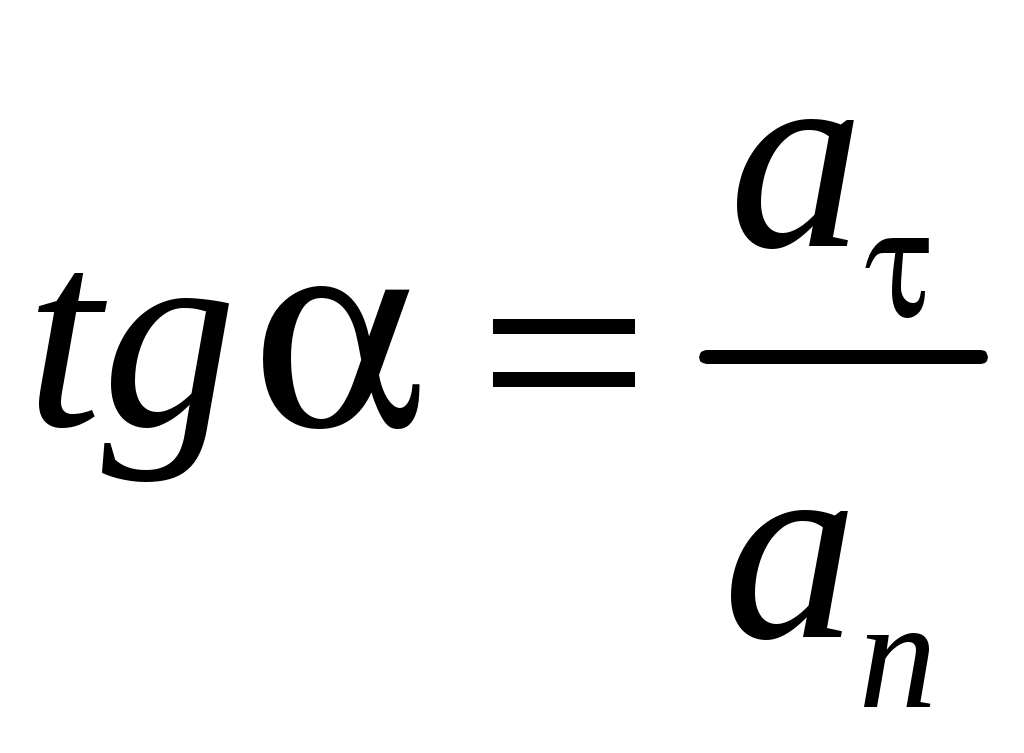 . .
|
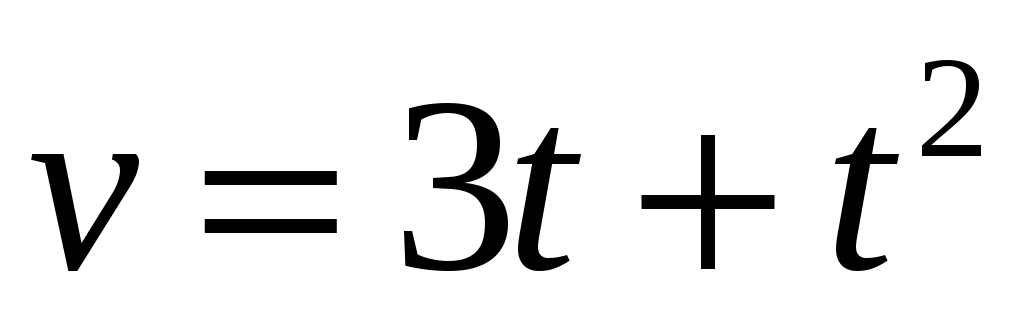 см/с см/с
|
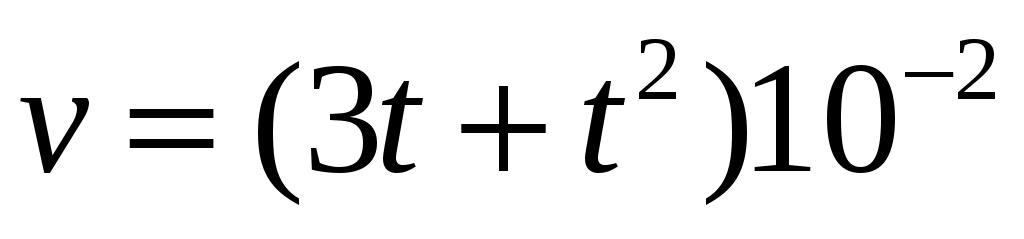 м/с м/с
|
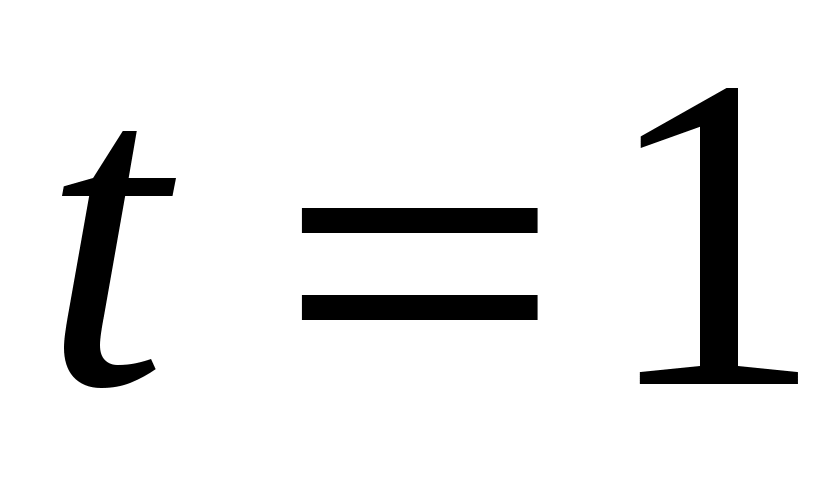 с с
|
|
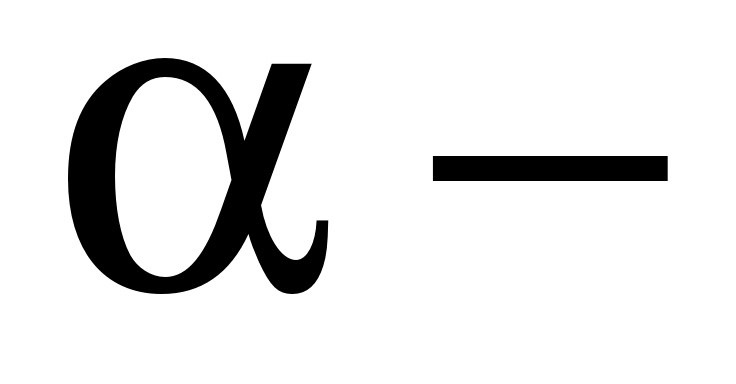 ? ?
|
|
Касательное ускорение по определению (1.23):
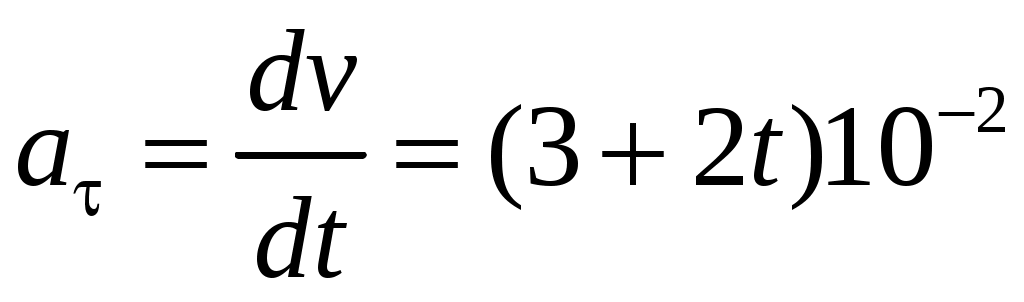 (м/с2). (м/с2).
Нормальное ускорение в соответствии с выражением (1.24):
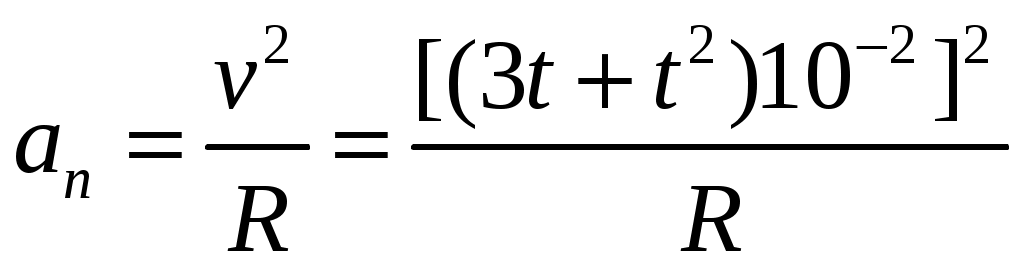 (м/с2). (м/с2).
Тогда тангенс искомого угла будет равен:
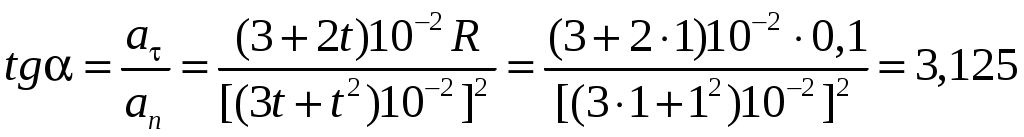 , ,
а сам искомый угол 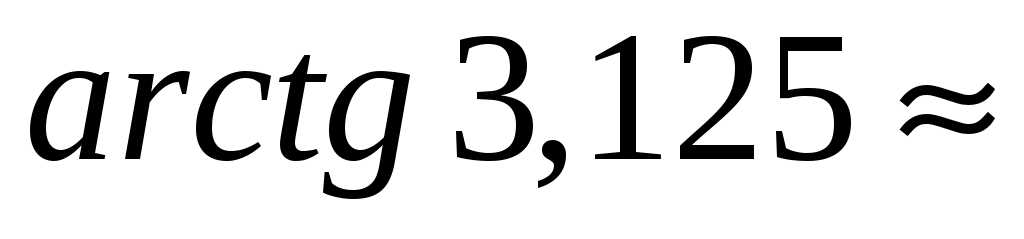 70о. 70о.
Полученный в данном задании результат будет под цифрой 4.
|
|
|
 Скачать 1.02 Mb.
Скачать 1.02 Mb.
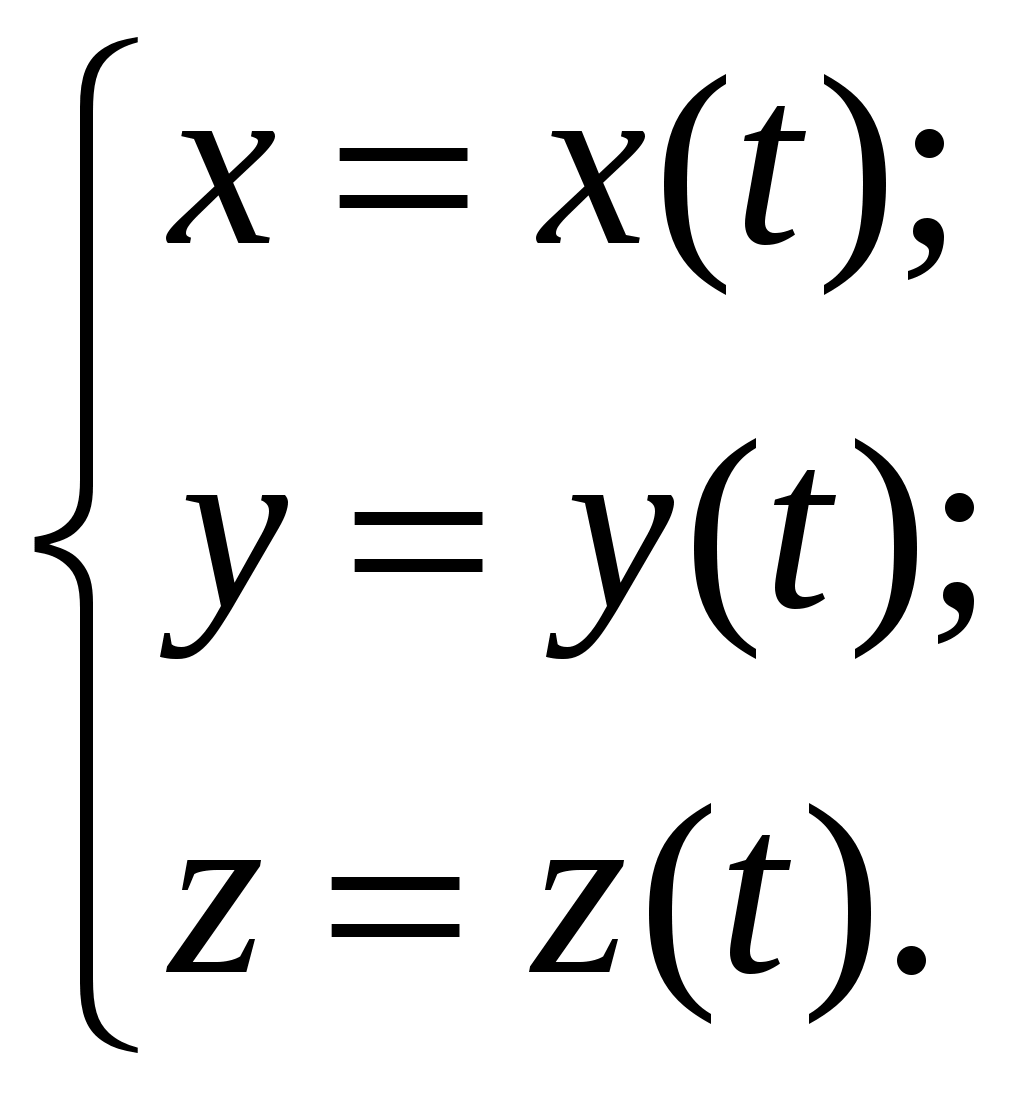
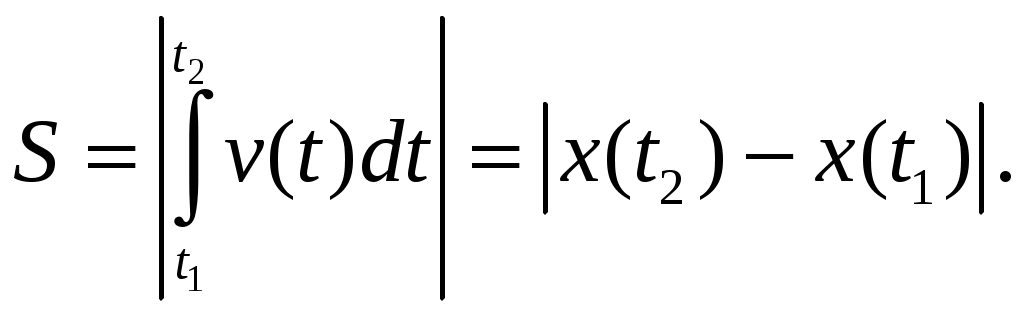 (1.13)
(1.13)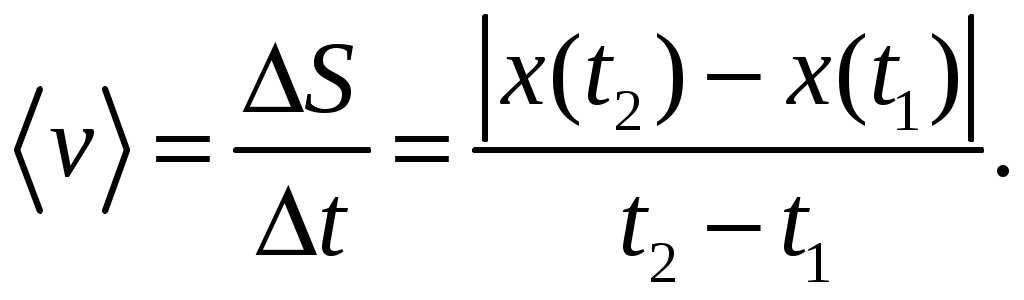 (1.14)
(1.14)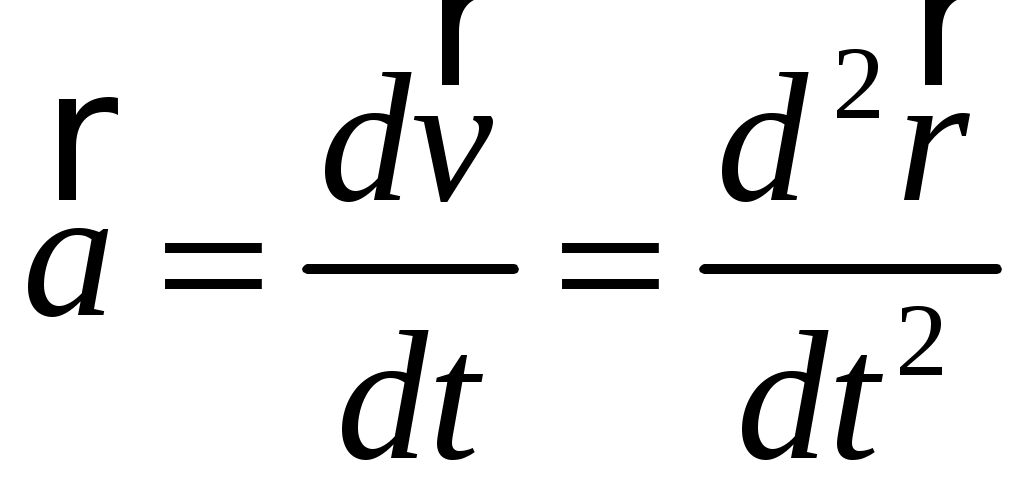 (1.14)
(1.14)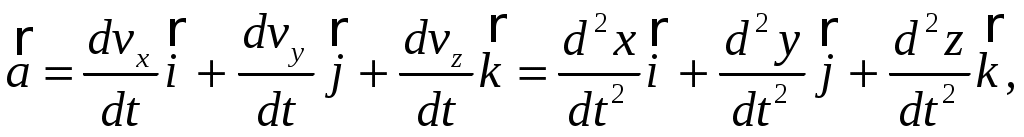 (1.15)
(1.15)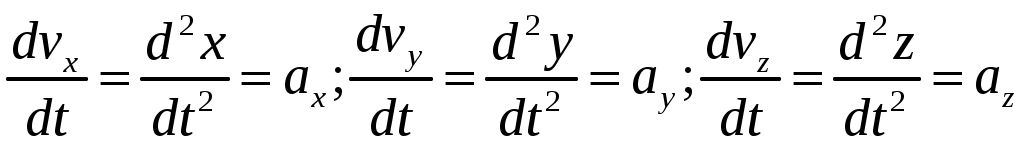 – проекции вектора ускорения на оси координат.
– проекции вектора ускорения на оси координат.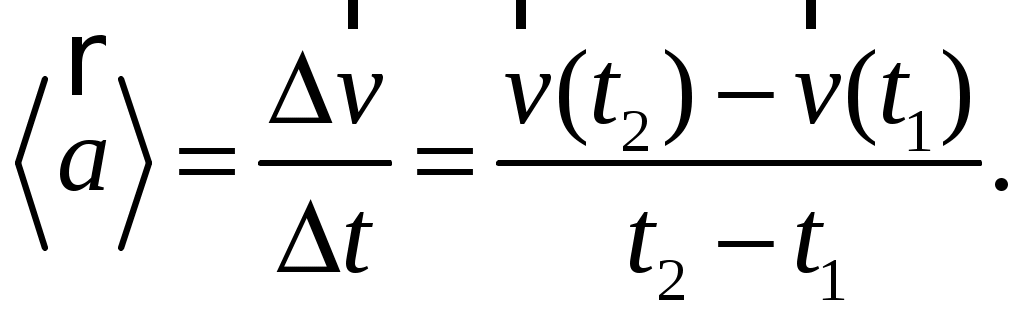 (1.17)
(1.17)
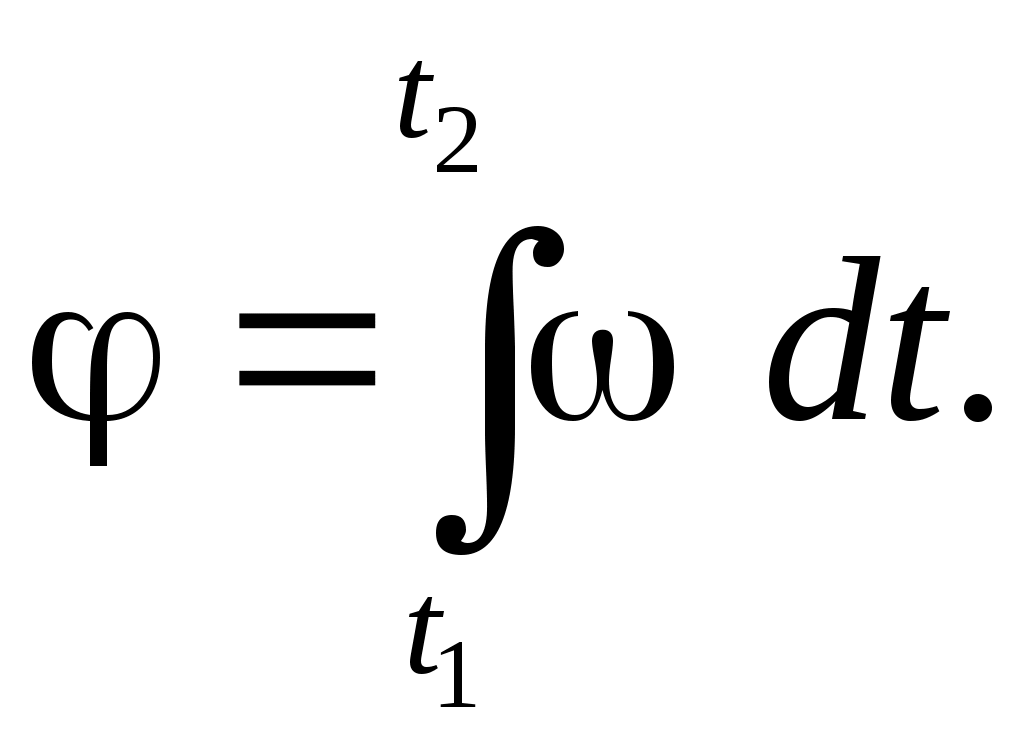
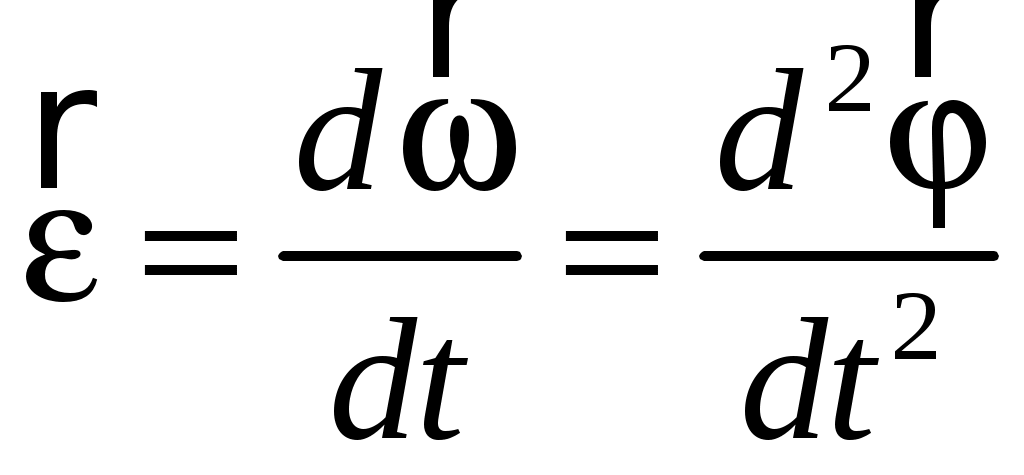 . (1.20)
. (1.20) оставляющая
оставляющая 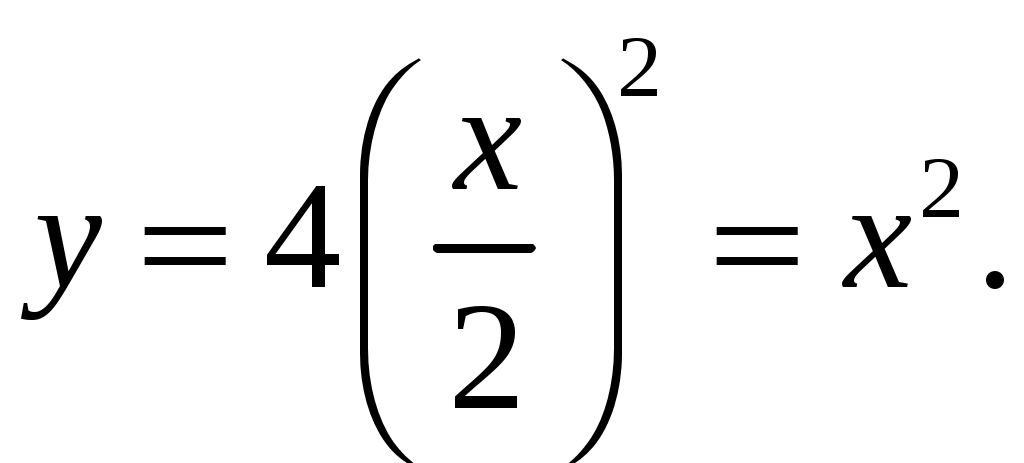
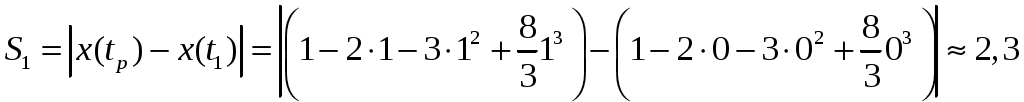 (м).
(м).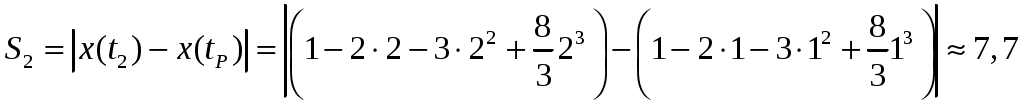 (м).
(м).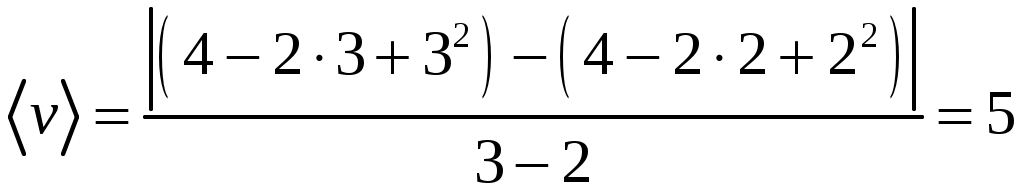 (м/с).
(м/с).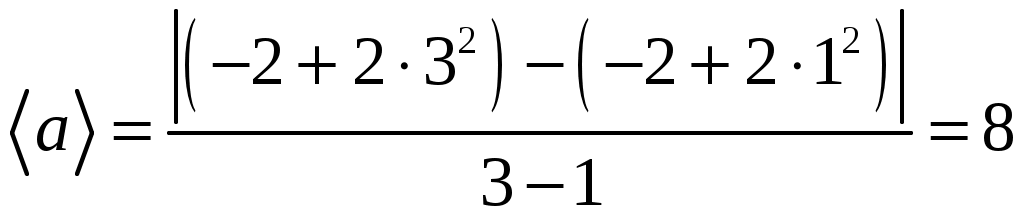 (м/с2).
(м/с2).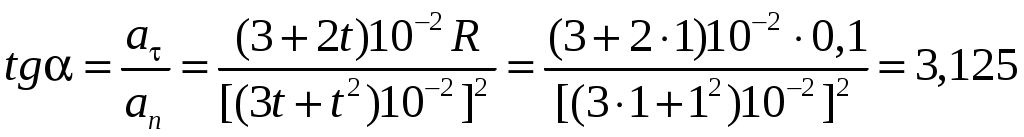 ,
,
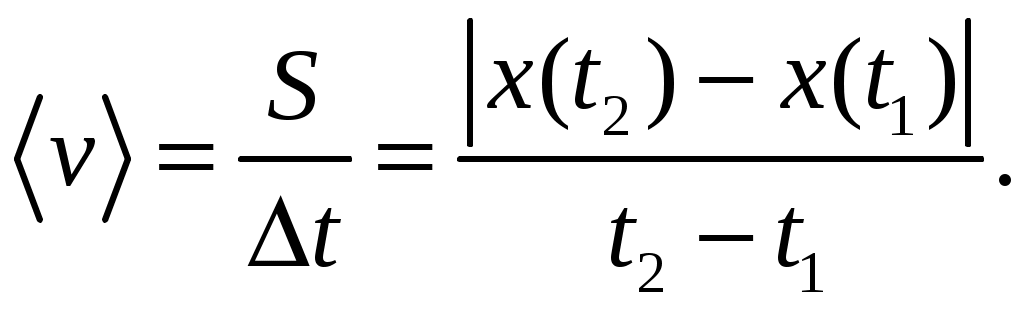
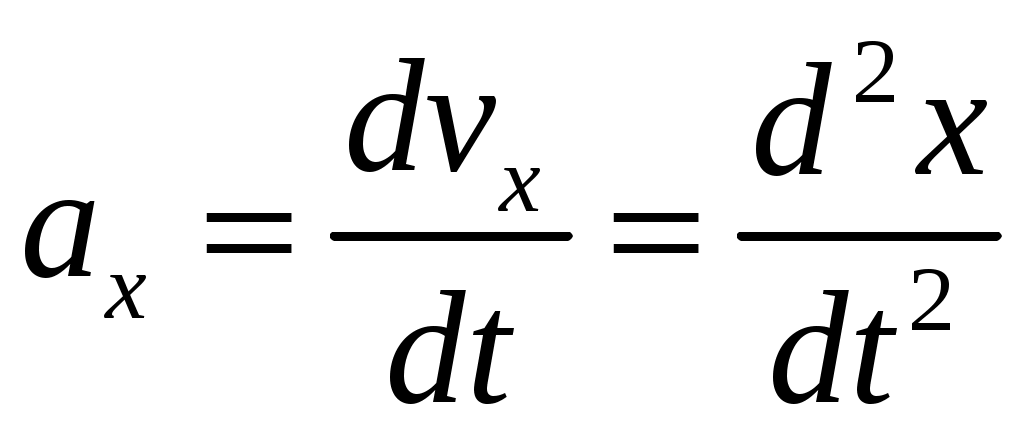 .
.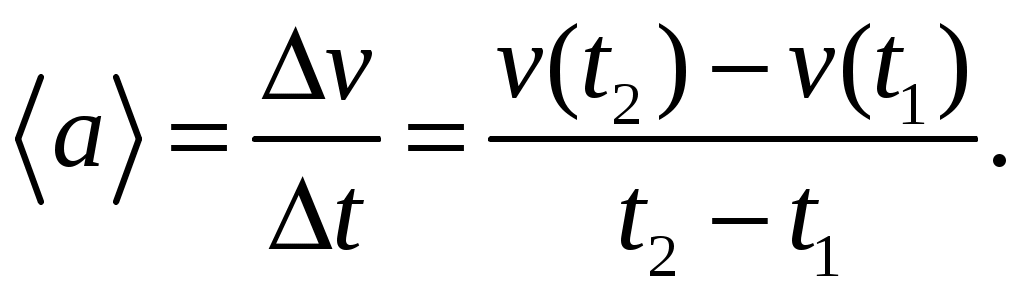

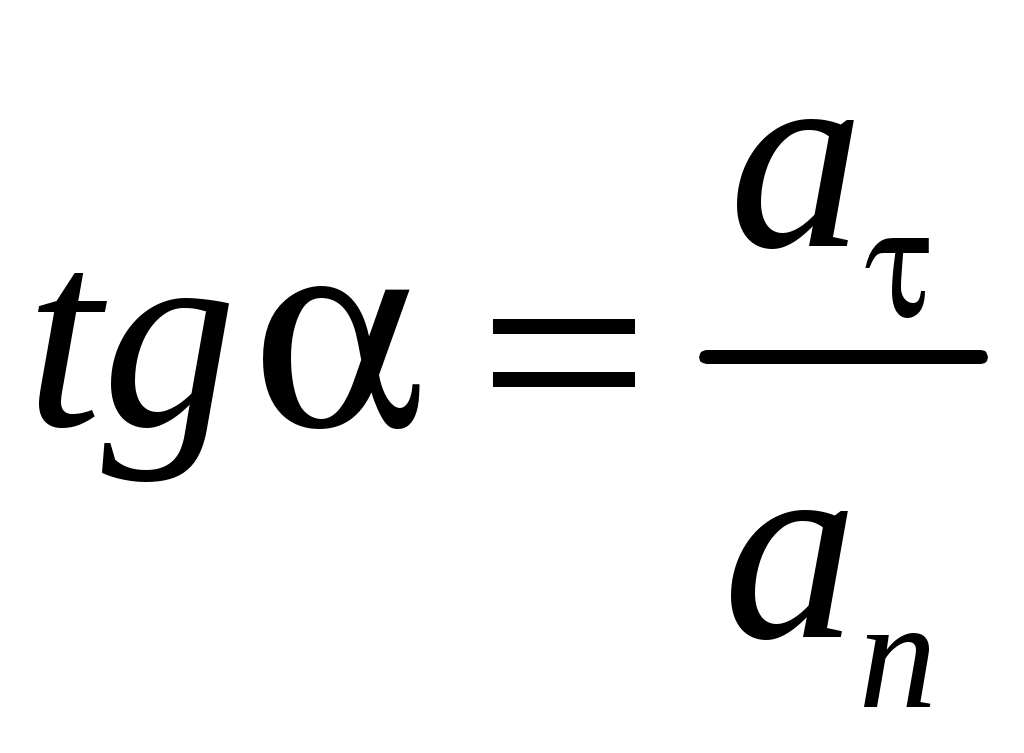 .
.