м/с2;
2) 0,4 м/с2;
|
3) 0,6 м/с2;
|
4) 0,8 м/с2.
|
1.47.
|
Если зависимость пройденного частицей пути по окружности радиусом 3 м задана уравнением 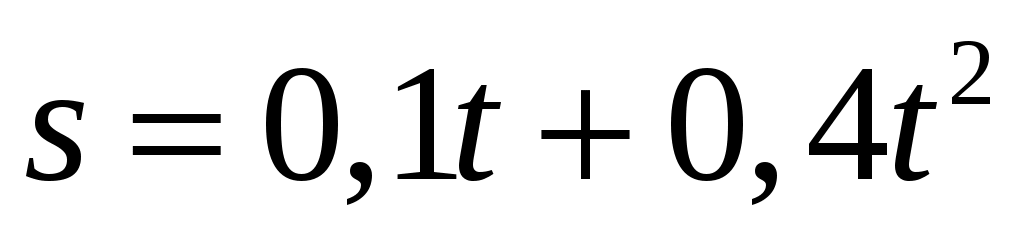 (м), то касательное ускорение частицы будет равно
|
1) 0,2 м/с2;
|
2) 0,4 м/с2;
|
3) 0,6 м/с2;
|
4) 0,8 м/с2.
|
1.48.
|
Частица движется по окружности радиусом 2 см, при этом зависимость ее пути от времени задана уравнением 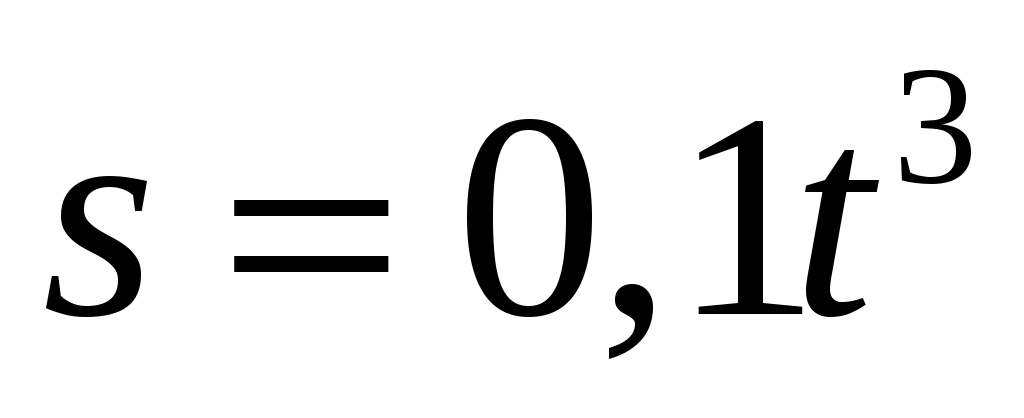 (см). Если через некоторый промежуток времени линейная скорость частицы приняла значение 0,3 м/с, то ее касательное ускорение в этот момент времени будет равно
|
1) 0,2 м/с2;
|
2) 0,4 м/с2;
|
3) 0,6 м/с2;
|
4) 0,8 м/с2.
|
1.49.
|
Если диск вращается вокруг неподвижной оси так, что его угловая координата определяется уравнением 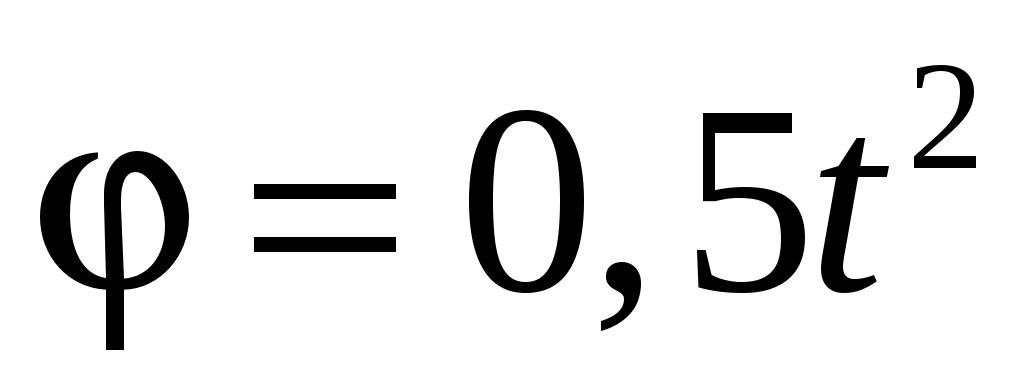 (рад), то к концу второй секунды от начала движения диска нормальное ускорение его точек, отстоящих от оси вращения на 80 см, будет равно
|
1) 3,1 м/с2;
|
2) 3,2 м/с2;
|
3) 3,3 м/с2;
|
4) 3,4 м/с2.
|
1.50.
|
Если диск радиусом 10 см вращается вокруг неподвижной оси так, что зависимость его угловой координаты определяется уравнением 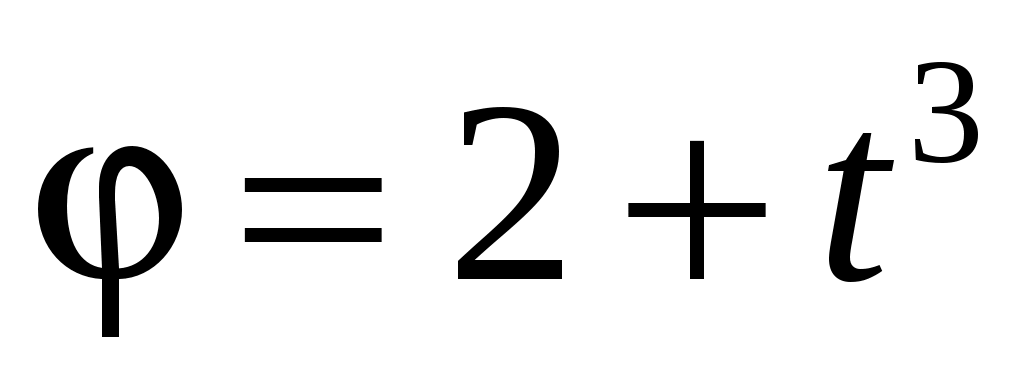 (рад), то через две секунды от начала движения для точек на ободе диска нормальное ускорение будет равно
|
1) 10 м/с2;
|
2) 12 м/с2;
|
3) 14 м/с2;
|
4) 16 м/с2.
|
1.51.
|
Если диск радиусом 10 см вращается вокруг неподвижной оси так, что его угловая координата определяется уравнением 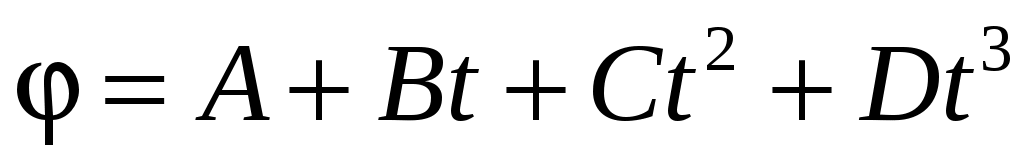 , где В = 1 рад/с; С = 1 рад/с2; D = 1 рад/с3, то к концу первой секунды от начала движения диска нормальное ускорение точек на его ободе будет равно
|
1) 3,6 м/с2;
|
2) 3,8 м/с2;
|
3) 4,0 м/с2;
|
4) 4,2 м/с2.
|
1.52.
|
Если колесо радиусом 0,1 м вращается так, что его угловая координата задана уравнением 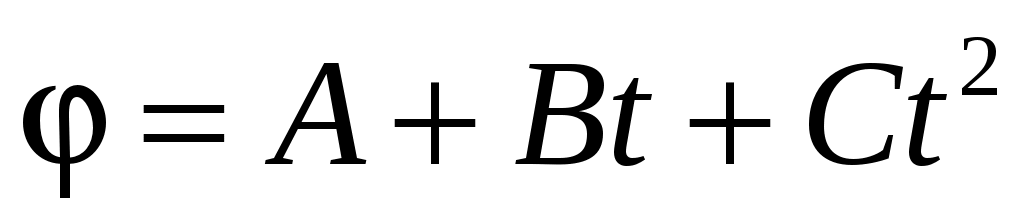 , где В = 2 рад/c; С = 1 рад/с2, то через две секунды после начала движения нормальное ускорение точек на ободе колеса будет равно
|
1) 3,6 м/с2;
|
2) 3,8 м/с2;
|
3) 4,0 м/с2;
|
4) 4,2 м/с2.
|
1.53.
|
Частица движется по окружности так, что ее угловая координата задана уравнением 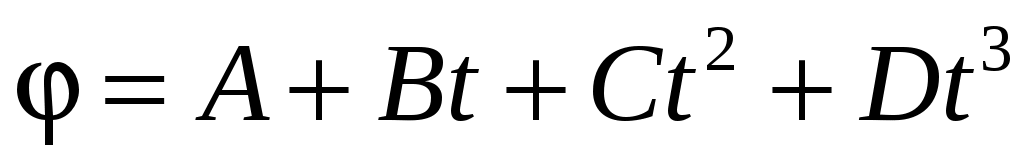, где В = 1 рад/с; С = 1 рад/с2; D = 1 рад/с3. Если к концу первой секунды движения частицы ее нормальное ускорение равно 1,8 м/с2, то радиус окружности будет равен
|
1) 5 см;
|
2) 10 см;
|
3) 15 см;
|
4) 20 см.
|
1.54.
|
Если нормальное ускорение частицы, движущейся по окружности радиусом 4 м, задается уравнением 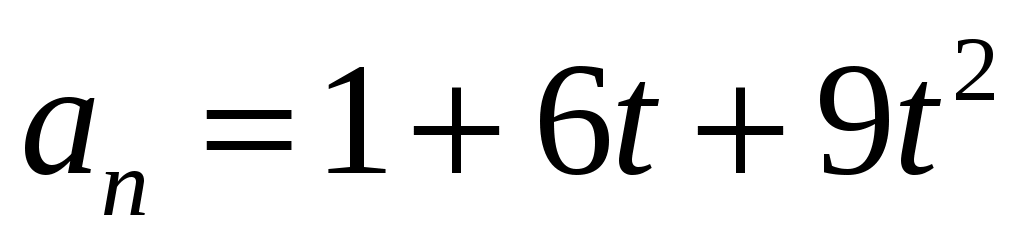 (м/с2), то для момента времени одна секунда от начала движения касательное ускорение частицы будет равно
|
1) 2 м/с2;
|
2) 4 м/с2;
|
3) 6 м/с2;
|
4) 8 м/с2.
|
1.55.
|
Если частица, двигаясь по окружности радиусом 2 см, через некоторый промежуток времени достигла значения скорости 0,3 м/с, то нормальное ускорение частицы в этот момент времени будет равно
|
1) 4,0 м/с2;
|
2) 4,5 м/с2;
|
3) 5,0 м/с2;
|
4) 5,5 м/с2.
|
1.56.
|
Зависимость пройденного частицей пути по окружности радиусом 3 м задана уравнением 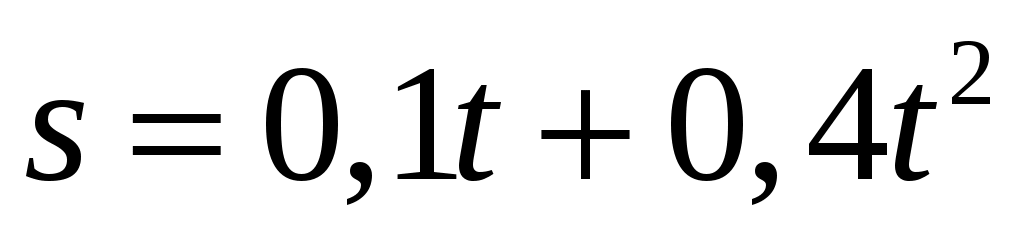(м). Нормальное ускорение частицы через одну секунду от начала ее движения будет равно
|
1) 0,1 м/с2;
|
2) 0,2 м/с2;
|
3) 0,3 м/с2;
|
4) 0,4 м/с2.
|
1.57.
|
Частица движется по окружности, причем зависимость ее пути от времени задана уравнением 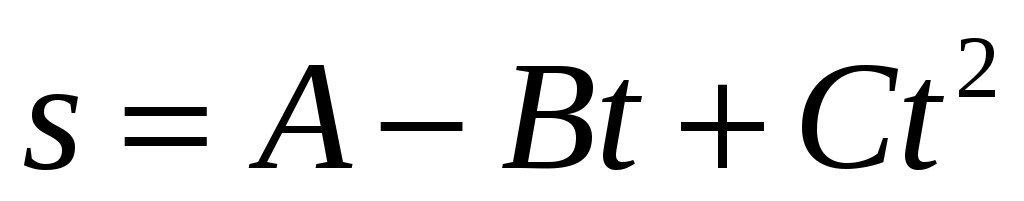 , где В = 2 м/с; С = 1 м/с2. Если в момент времени две секунды нормальное ускорение частицы равно 0,5 м/с2, то ее угловая скорость через три секунды после начала движения частицы будет равна
|
1) 0,5 рад/с;
|
2) 1,0 рад/с;
|
3) 1,5 рад/с;
|
4) 2,0 рад/с.
|
1.58.
|
Частица движется по окружности, причем зависимость ее пути от времени задана уравнением 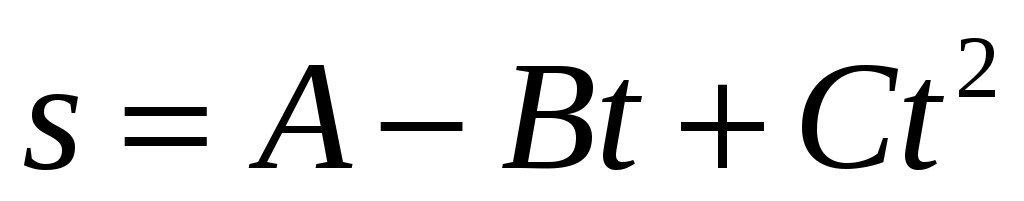, где В = 2 м/с; С = 1 м/с2. Если в момент времени две секунды нормальное ускорение частицы равно 0,5 м/с2, то ее касательное ускорение через три секунды после начала движения частицы будет равно
|
1) – 2 м/с2;
|
2) – 1 м/с2;
|
3) 1 м/с2;
|
4) 2 м/с2.
|
1.59.
|
Если нормальное ускорение частицы, движущейся по окружности радиусом 4 м, задается уравнением 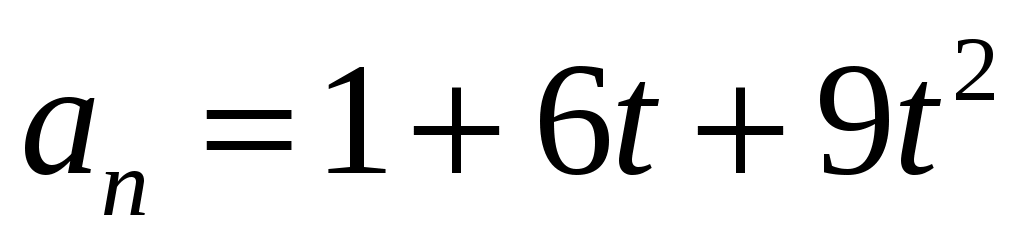(м/с2), то момент времени от начала движения, когда частица будет иметь касательное ускорение 6 м/с2; будет
|
1) любой;
|
5) 0;
|
2) 1 с;
|
3) 2 с.
|
1.60.
|
Частица движется по окружности, причем зависимость ее пути от времени задана уравнением 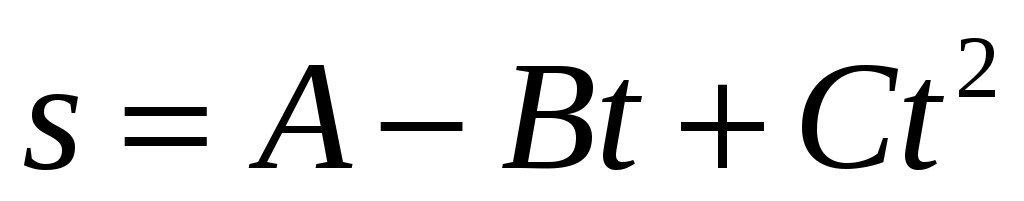, где В = 2 м/с; С = 1 м/с2. Если в момент времени две секунды нормальное ускорение частицы равно 0,5 м/с2, то ее нормальное ускорение через три секунды после начала движения частицы будет равно
|
1) 1 м/с2;
|
2) 2 м/с2;
|
3) 3 м/с2;
|
4) 4 м/с2.
|
1.61.
|
Если диск радиусом 10 см вращается вокруг неподвижной оси так, что зависимость его угловой координаты определяется уравнением 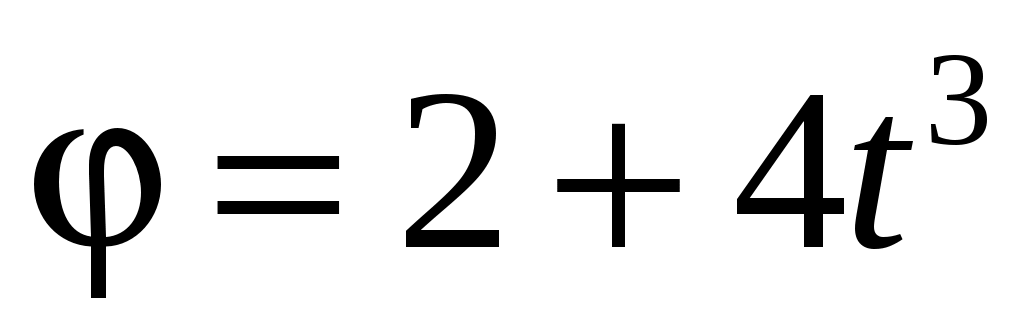 (рад), то угол поворота диска, при котором вектор полного ускорения составит с радиусом диска угол 45о, будет равен
|
1) 1 рад;
|
2) 2 рад;
|
3) 3 рад;
|
4) 4 рад.
|
1.62.
|
Если колесо радиусом 10 см вращается так, что линейная скорость точек на его ободе задана уравнением 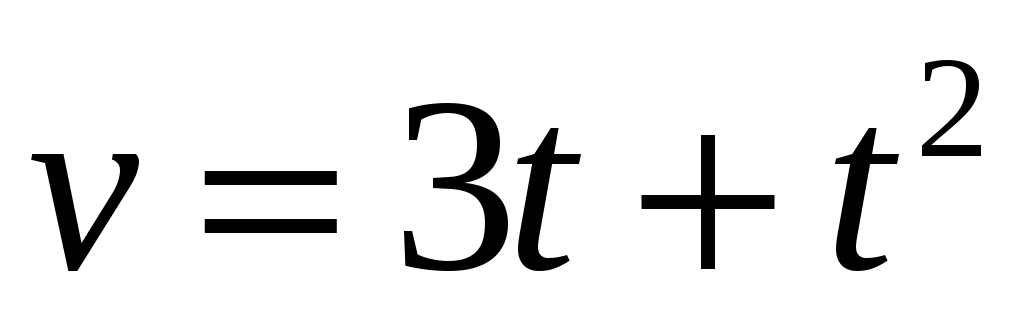 (см/с), то спустя одну секунду после начала движения угол между вектором полного ускорения и радиусом колеса будет равен
|
1) 30о;
|
2) 35о;
|
3) 70о;
|
4) 75о.
|
1.63.
|
Если колесо радиусом 10 см вращается так, что линейная скорость точек на его ободе задана уравнением 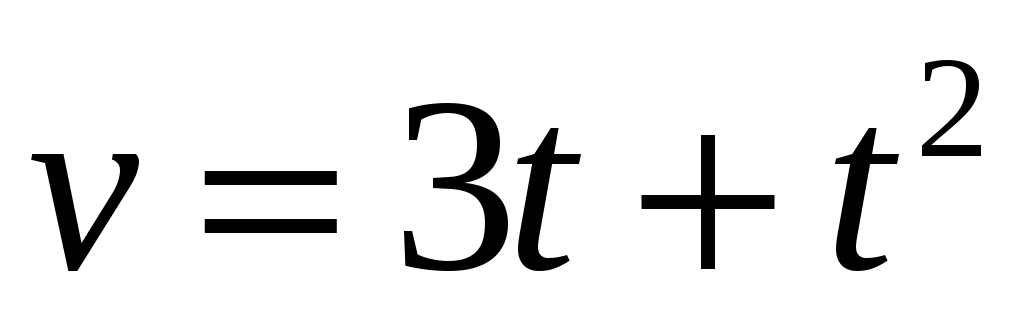(см/с), то спустя две секунды после начала движения угол между вектором полного ускорения и радиусом колеса будет равен
|
1) 30о;
|
2) 35о;
|
3) 70о;
|
4) 75о.
|
1.64.
|
Если частица начинает движение по окружности радиусом 12,5 см с постоянным касательным ускорением 0,5 см/с2, то момент времени, при котором вектор полного ускорения образует с вектором линейной скорости угол 45о, будет равен
|
1) 5 с;
|
2) 10 с;
|
3) 15 с;
|
4) 20 с.
|
1.65.
|
Если частица начинает движение по окружности радиусом 12,5 см с постоянным касательным ускорением 0,5 см/с2, причем через некоторое время вектор полного ускорения образует с вектором линейной скорости угол 45о, то путь, пройденный частицей за указанное время, будет равен
|
1) 6,00 см;
|
2) 6,25 см;
|
3) 6,50 см;
|
4) 6,75 см.
|
1.66.
|
Если диск вращается вокруг неподвижной оси так, что его угловая координата определяется уравнением 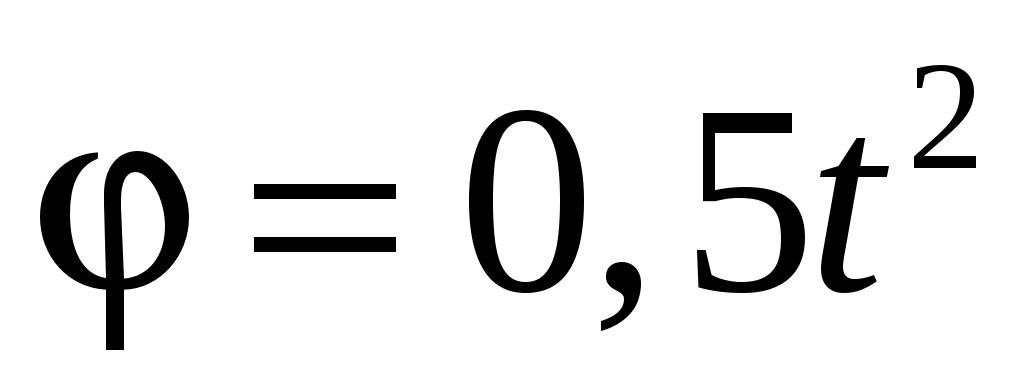(рад), то к концу второй секунды от начала движения диска полное ускорение его точек, отстоящих от оси вращения на 80 см, будет равно
|
1) 3,0 м/с2;
|
2) 3,1 м/с2;
|
3) 3,2 м/с2;
|
4) 3,3 м/с2.
|
1.67.
|
Если диск радиусом 10 см вращается вокруг неподвижной оси так, что его угловая координата определяется уравнением 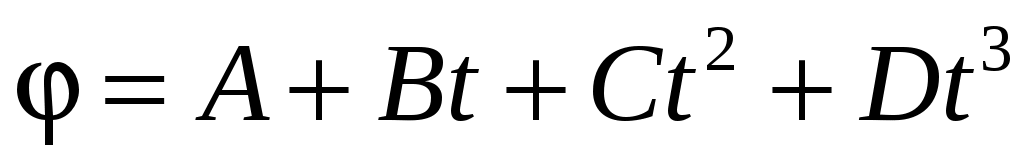, где В = 6 рад/с; С = 4 рад/с2; D = 2 рад/с3, то в момент времени t = 0 полное ускорение точек на ободе диска будет равно
|
1) 0,5 м/с2;
|
2) 1,0 м/с2;
|
3) 1,5 м/с2;
|
4) 2,0 м/с2.
|
1.68.
|
Диск вращается вокруг неподвижной оси так, что его угловая координата определяется уравнением 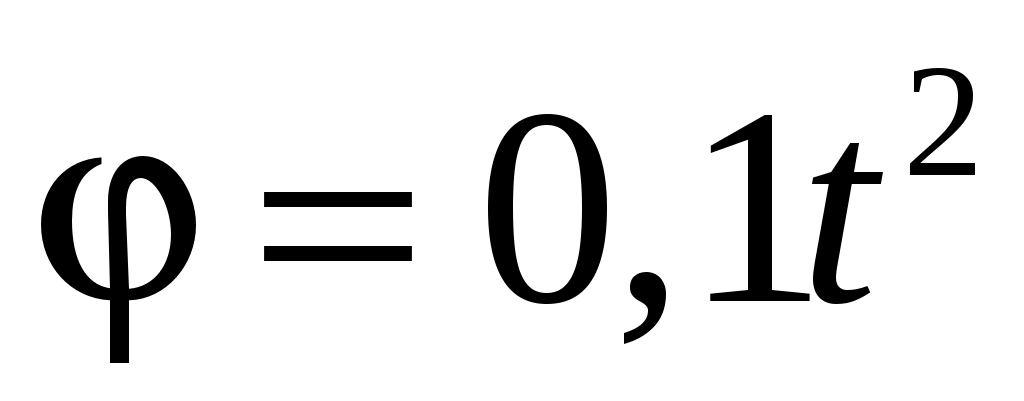 (рад). Если линейная скорость некоторой точки диска к концу второй секунды от начала его движения равна 0,4 м/с, то полное ускорение этой точки будет равно
|
1) 0,15 м/с2;
|
2) 0,25 м/с2;
|
3) 0,35 м/с2;
|
4) 0,45 м/с2.
|
1.69.
|
Если зависимость пути, пройденного частицей по окружности радиусом 3 м, задана уравнением 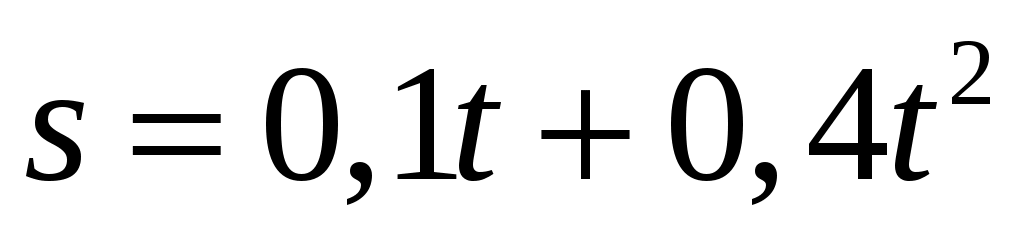(м), то полное ускорение частицы через одну секунду от начала ее движения будет равно
|
1) 0,81 м/с2;
|
2) 0,82 м/с2;
|
3) 0,83 м/с2;
|
4) 0,84 м/с2.
|
1.70.
|
Частица движется по окружности, причем зависимость ее пути от времени задана уравнением 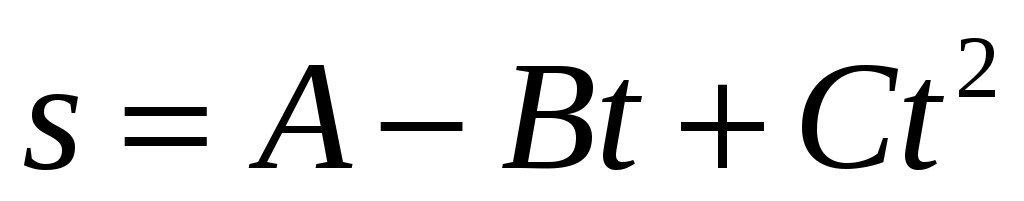, где В = 2 м/с; С = 1 м/с2. Если в момент времени две секунды нормальное ускорение частицы равно 0,5 м/с2, то ее полное ускорение через три секунды после начала движения частицы будет равно
|
1) 2,4 м/с2;
|
2) 2,6 м/с2;
|
3) 2,8 м/с2;
|
4) 3,0 м/с2.
|
1.71.
|
Если нормальное ускорение частицы, движущейся по окружности радиусом 4 м, задано уравнением 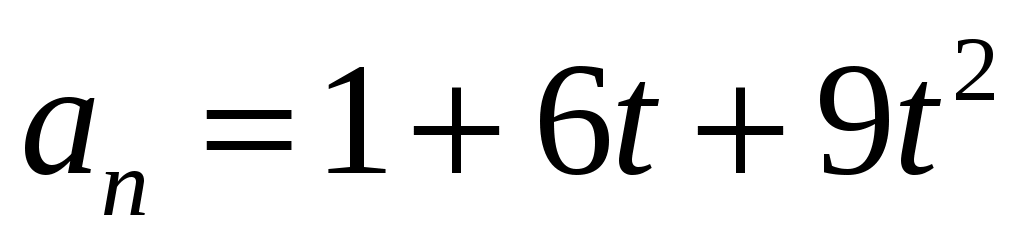(м/с2), то полное ускорение частицы для момента времени одна секунда от начала ее движения будет равно
|
1) 17 м/с2;
|
2) 16 м/с2;
|
3) 15 м/с2;
|
4) 14 м/с2.
|
1.72.
|
Если касательное ускорение частицы, начинающей движение по окружности радиусом 3,5 м, задано уравнением 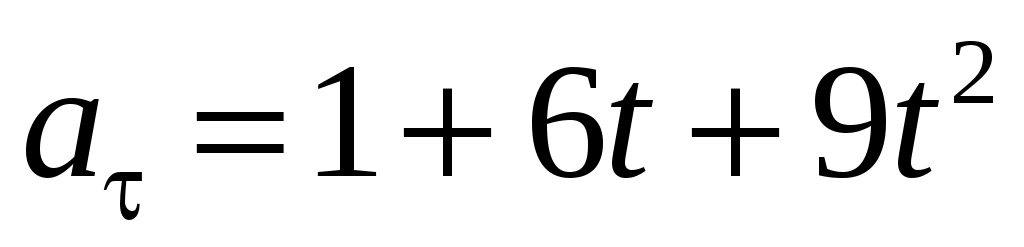 (м/с2), то полное ускорение частицы для момента времени одна секунда от начала ее движения будет равно
|
1) 11 м/с2;
|
2) 21 м/с2;
|
3) 31 м/с2;
|
4) 41 м/с2.
|
|
Скачать 1.02 Mb.