Тест по Теории вероятностей и Математической статистике по темам. Элементы комбинаторики Перестановки вычисляются по формуле
 Скачать 432 Kb. Скачать 432 Kb.
|
|
Г) M(x:y)=М(x):М(y) Найти верное равенство А) D(c)=c Б) D(cх)=cD(x) В) D(cх)=c2D(x) Г) D(c)=1 Дисперсия постоянной величины равна А)0 Б) 1 В) этой величине Г) квадрату этой величины Найти верное высказывание А) дисперсия принадлежит множеству целых чисел Б) При вынесении постоянного множителя за знак дисперсии, необходимо его возвести в квадрат В) для зависимых случайных величин х и у дисперсия алгебраической суммы равна сумме дисперсий слагаемых Г) дисперсия постоянной величины равна этой величине Найти неверное свойство дисперсии А) D(x)≥0 Б) D(с)=0 В) D(cх)=c2D(x) Г) D(x-y)=D(x)+D(y) В экономике среднее квадратическое отклонение называют А) стандартное Б) идеальное равновесие В) центр распределения ДСВ Г) среднее значение ДСВ Какое распределение относится к дискретной случайной величине? А) биноминальное Б) нормальное В) показательное Г) равномерное Какое распределение не относится к дискретной случайной величине? А) Пуассона Б) биноминальное В) геометрическое Г) равномерное Какое распределение строится на основе схемы Бернулли А) геометрическое Б) Пуассона В) биноминальное Г) показательное Закон распределения Пуассона А) pn(m)= Б) pn(k)= В) p(k)=qk-1p Г) p(x)= 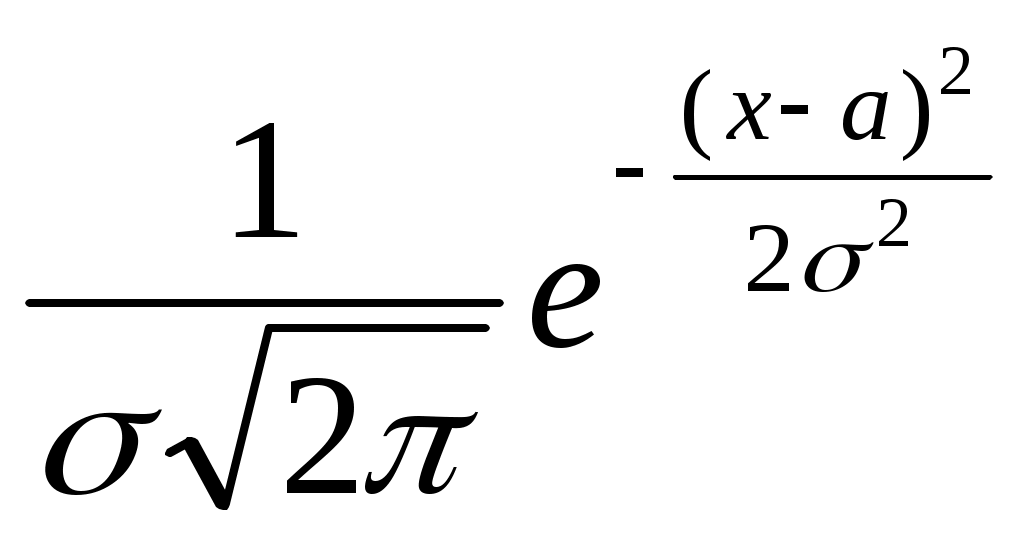 Геометрическое распределение А) p(x)= 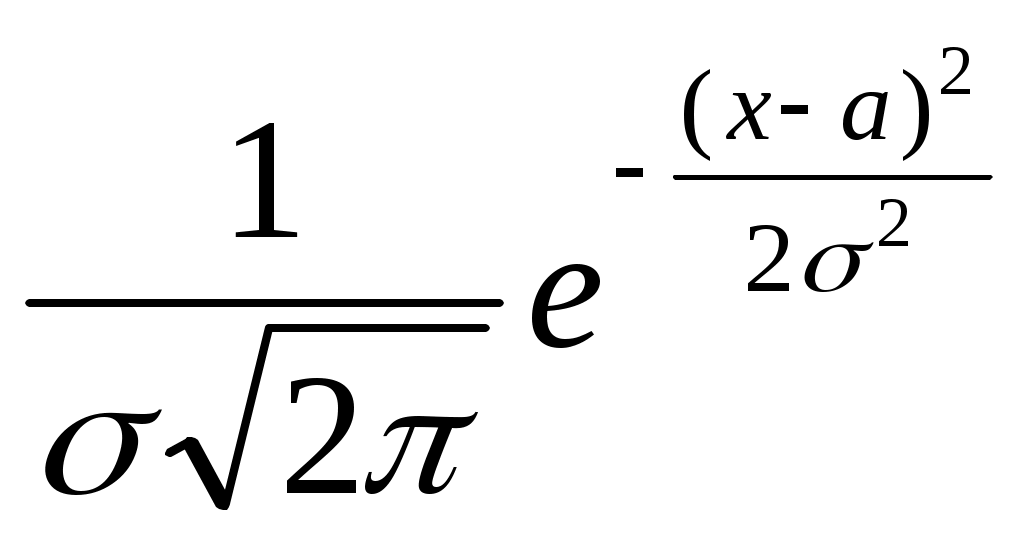 Б) p(k)=qk-1p В) pn(k)= Г) pn(m)= По заданному ряду распределения найти функцию распределения
 0 x 0 xА) F(x)= 0,1 0 0,3 1 0,6 2 1 x>3 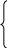 0,1 x 0,1 xБ) F(x)= 0,2 0 0,3 1 0,4 2 1 x>3  0,1 x 0,1 xВ) F(x)= 0,2 1 0,3 2 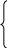 0,4 x>3 0,4 x>30 x<0 Г) F(x)= 0,1 0 0,3 1 0,6 2 1 x>3 По заданной функции распределения построить ряд распределения дискретной случайной величины  0 x 0 xF(x)= 0,05 0 0,13 1 0,63 2 1 x>3 А)
Б)
В)
Г)
Найти математическое ожидание от функции z=x+2y-5, если М(х)=2, М(у)=3 А) М(z)=0 Б) М(z)=3 В) М(z)=8 Г) М(z)=9 Найти дисперсию случайной величины z=3x-2y+14, если D(x)=2, D(y)=1 А) D(z)=18 Б) D(z)=28 В) D(z)=14 Г) D(z)=16 Ответы к тесту №3
|
