Элементы математического анализа

• Название: Элементы математического анализа
• Дата: 25.04.2021
• Размер: 273.5 Kb.
• Имя файла: 7.doc
• Тип: Документы; #198430

Элементы математического анализа
К математическому анализу относят совокупность разделов математики, посвященных исследованию функций методами дифференциального и интегрального исчислений. Обычно в курс математического анализа включают также разделы: ряды и функции комплексного переменного.
Производная

Производной функции у = f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):

.

Геометрический смысл производной заключается в том, что производная f'(x₀) есть угловой коэффициент (тангенс угла наклона α) касательной, проведенной к кривой у = f(x) в точке х₀, то есть k = f'(x₀) (рис. 4.1).

Обычно производная характеризует скорость изменения различных функций. Например, скорость движения — это производная от пути по времени s'_t. Экономическим приложением производной, например, может быть нахождение производительности труда в момент t₀ по функции количества произведенной продукции u = u(t).

С ее помощью находятся такие показатели, как предельные затраты, предельная выручка, предельный спрос, предельная производительность и др. Внешним признаком наличия связи с производной в экономических приложениях является присутствие термина «предельный».

Предельные затраты — это производная от затрат по выпуску продукции.

Предельная производительность — это производная от выпуска продукции по за­тратам данного ресурса.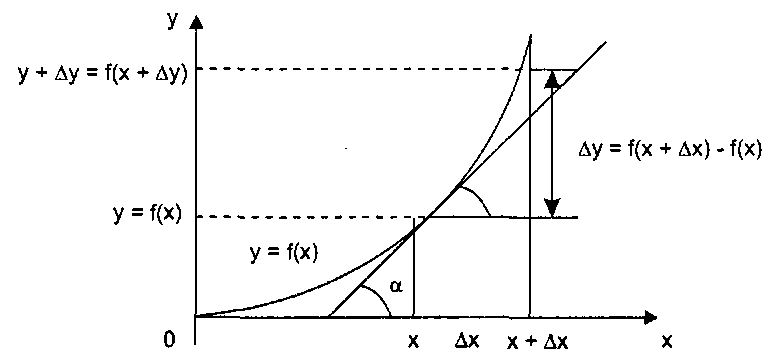



Рис. 4.1. Геометрический смысл производной Предельный спрос — это производная от спроса по цене.
Поскольку производная f'(x) сама является функцией, то она также может иметь производную. Продолжая дальше, можно сказать, что производной n-го порядка называется производная от производной (n-1)-го порядка. Обозначаются производные высших порядков как: f''(x) — второго порядка (или вторая производная), f'''(x) — третьего порядка (или третья производная). Для обозначения производных более высокого порядка используются арабские цифры в скобках или римские цифры (f⁽⁴⁾(x)).

Продифференцировать функцию (найти ее производную) можно, используя таблицу производных простейших функций и правила дифференцирования:

Таблица производных простейших функций

f(x)	с = const	x	xn	√х	sinх	cosx
f'(x)	0	1	n * хn-1	1 / 2√x	cosx	-sinx
f(x)	tgx	аx	ех	logаx	Inx
f'(x)	1 / cos2x	аx * Inа	ех	1 / х*Inа	1 / x

Правила дифференцирования:

- производная суммы функций:

(f(x) + g(x) +... + h(x))' = f'(x) + g'(x) +... + h'(x);

- производная суммы функций равна сумме производных

(k*f(x))' = k*f'(x).

Постоянный коэффициент можно выносить за знак производной.

- производная произведения:

(f(x) * g(x))' = f'(x) * g(x) + f(x) g'(x).

- производная дроби (частного, отношения):

;

- производная сложной функции:



Однако в ряде случаев простейшими правилами дифференцирования воспользоваться достаточно сложно. Например, когда функция задана таблично или получена в результате наблюдений. В этих случаях прибегают к численным методам дифференцирования.

Численное дифференцирование очень чувствительно к ошибкам, вызванным неточностью исходных данных, отбрасываемых членов ряда и т. д., и поэтому должно применяться с осторожностью.

Существуют различные формулы численного дифференцирования. Из них простейшими являются явные трехточечные формулы, в частности:

.

Здесь у_-1, у₀ и у₁ — три последовательные точки, Δх — достаточно малый шаг дис­кретизации. Погрешность вычисления производной Δ по формуле (4.1) может быть оценена из выражения:

,

где x_-1 < ξ < x₁. Когда экспериментальные данные зашумлены более сильно (имеют большие погрешности) используют методы дифференцирования по большему числу точек. Примером может являться так называемая формула численного дифференцирования после сглаживания:

.
Упражнения

1. Зависимость спроса на товар от цены выражается формулой:

.

Построить график функции этой зависимости в диапазоне p € [1; 3] с шагом Δр = 0,1. С какой скоростью изменяется спрос при цене р = 2?

2. Зависимость полных издержек производства k от объема производства х выражается формулой:

k = х³ - 4х² + 9х.

Изобразите графически изменение издержек с изменением объема производства в диапазоне х € [1; 5] с шагом Δx = 0,2. Постройте график скорости изменения издержек в диапазоне х € [1,2; 4,8] с шагом Δx = 0,2.
Определенный интеграл

Пусть на отрезке [а, b] задана функция у = f(x), и отрезок [а, b] разбит на и элементарных отрезков точками х₀,х₁,...,х_n:

а = х₀ < х₁ < х₂ < ... < х_n =b.

На каждом отрезке [х_i-1, х_i] разбиения выбрана некоторая точка ξ_i и положено, что Δx_i = х_i - х_i-1, где i = 1,2,...,n. Тогда сумма вида:

(4.2)

называется интегральной суммой для функции у = f(x) на [а, b]. Интегральная сумма зависит как от способа разбиения отрезка [а, b] точками х₀, х₁,…,х_n, так и от выбора точек ξ₀, ξ₁,…,ξ_n, на каждом из отрезков разбиения Δx_i = х_i - х_i-1, i = 1,2,...,n. Обозначим через max Δх_i максимальную из длин отрезков [х_i-1, х_i], где i = 1,2,...,n.

Тогда определенным интегралом от функции y = f(x) на [а, b] называется предел интегральной суммы при стремлении max Δх_i к нулю, если он существует, конечен и не зависит от способа выбора точек х₁, х₂,… и точек ξ₁, ξ₂,…. Определенный интеграл обозначается



а функция f(х) называется интегрируемой на отрезке [а, b], то есть:

. (4.3)

При этом число а называется нижним пределом определенного интеграла, число b — его верхним пределом, функция f(x) — подынтегральной функцией, выражение f(x)dx — подынтегральным выражением, а задача о нахождении - интегрированием функции f(х) на отрезке [а, b].

Геометрический смысл определенного интеграла заключается в следующем. Если функция у = f(х) неотрицательна на отрезке [а, b], где а < b, то 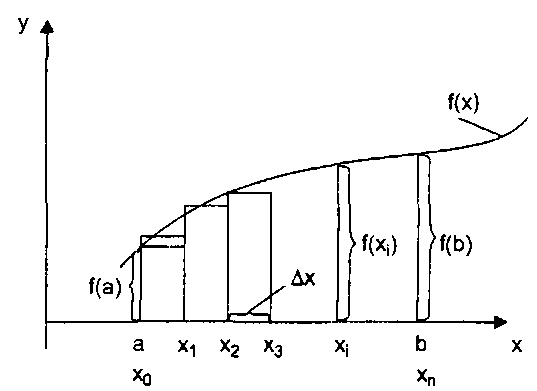численно равен площади S под кривой у = f(х) на [а, b] (рис. 4.3). Действительно, отдельное слагаемое интегральной суммы (4.2) равно площади S, прямоугольника со сторонами Δх_i и f(х_i) (согласно определению значение определенного интеграла не зависит от способа выбора точек ξ₁, ξ₂,…), где i = 1,2,…,n (рис. 4.3). Поэтому вся интегральная сумма (4.2) равна площади S_л = S₁ + S₂ + ... + S_n под ломаной, образованной на каждом из отрезков [х_i-1, х_i] прямыми, параллельными оси абсцисс. При стремлении max Δх_i к нулю ломаная неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой S_л = S.


Рис. 4.3. Диаграмма, поясняющая геометрический смысл определенного интеграла
В экономических приложениях, например, определенный интеграл может выражать объем произведенной продукции (u) при известной функции производительности труда (f(t)):

.

Обычно для нахождения определенного интеграла используется формула Ньютона-Лейбница:

, (4.4)

где F(a) и F(b) первообразные для f(х) в точках а и b. Первообразной функцией для функции f(х) на промежутке X называется функция F(x), если в каждой точке х этого промежутка F'(x) = f(х).

Однако применение формулы (4.4) на практике связано с существенными трудностями, возникающими при нахождении первообразной в случае усложнения подынтегральной функции. Поэтому в приложениях используют так называемые численные методы, позволяющие найти приближенное значение искомого интеграла с требуемой точностью. Этот подход оказывается особенно предпочтительным при использовании компьютеров для нахождения интегралов.

Существует значительное количество численных методов вычисления интегралов. Они основаны на разных способах нахождения площади под кривой f(х) (рис. 4.3.):

- как суммы элементарных прямоугольников — метод прямоугольников:

; (4.5)

- как суммы элементарных трапеций — метод трапеций: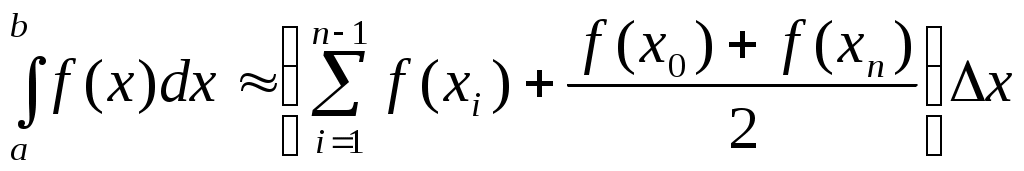

. (4.6)

Существуют также метод Симпсона и ряд других.

Формула метода прямоугольников (4.5) получается, если отрезок интегрирования [а, b] разбить на n равных частей длиной

.

На каждом из отрезков разбиения [х_i-1, х_i] участок кривой у = f(х) заменяется отрезком прямой, параллельным оси абсцисс. Тогда:

,

где S₁, S₂,…,S_n — площади прямоугольников на каждом из отрезков разбиения. Отдельное слагаемое S_i равно площади прямоугольника со сторонами Δх и f(х_i), где i = 1,2,…,n (рис. 4.3). Отсюда получается формула (4.5). Метод прямоугольников является простейшим, но и наименее точным.

Более точно определенный интеграл может быть вычислен по формуле трапеций (4.6). В этом случае, в отличие от метода прямоугольников, на каждом из отрезков разбиения [х_i-1, х_i] участок кривой у = f(х) заменяется хордами, стягивающими концевые точки. Тогда, отдельное слагаемое интегральной суммы S_i равно площади трапеции с основаниями f(х_i) и f(х_i-1) и высотой Δх, где i = 1,2,…,n. То есть:

.

Складывая площади элементарных трапеций и приводя подобные члены, получаем формулу (4.6).

Погрешность (Δ) вычисления определенного интеграла по формуле трапеций (S(n)):



может быть оценена из выражения:

,

где М₂ — максимальное значение модуля второй производной f(x) подынтегральной функции у = f(х) на [а, b].
Упражнения

3. Методом прямоугольников и методом трапеций найти следующие интегралы:

1) при Δx=0,1;

2) при Δx=0,1.

4. Найти объем продукции, произведенной за 4 года, если функция производительности труда имеет вид f(х) = (1 + t)е^3t, методом трапеций с шагом Δt = 0,2.
Ряды

При решении многих прикладных математических задач приходится рассматривать суммы, составленные из большого количества слагаемых, в том числе и из бесконечного множества слагаемых. Задача суммирования бесконечного множества слагаемых решается в теории рядов.
Числовые последовательности

Числовой последовательностью называется бесконечное множество чисел u₁, u₂,…,u_n расположенных в определенном порядке одно за другим. Числа, входящие в последовательность, называются ее членами. Последовательность считается заданной, если известен закон ее образования, то есть правило, по которому можно определить любой член последовательности. Примерами последовательностей являются натуральный ряд, арифметическая прогрессия, геометрическая прогрессия и т. д.

Пределом последовательности u₁, u₂,…,u_n называется число U, к которому числа u_n подходят сколь угодно близко, если такое число U существует для данной последовательности. Предел последовательности обозначается как

.

Широко распространенными числовыми последовательностями являются арифметическая и геометрическая прогрессии.

Арифметической прогрессией называется такая числовая последовательность, в которой каждый последующий член получается из предыдущего прибавлением определенного числа а, называемого разностью прогрессии. Если а > 0, прогрессия называется возрастающей, если а < 0 — убывающей.

и . (4.7)

Здесь S_n — сумма первых n членов прогрессии.

Геометрической прогрессией называется такая числовая последовательность, в которой каждый последующий член получается из предыдущего умножением его на определенное число q, называемое знаменателем (основанием) прогрессии. Если q > 1, прогрессия называется возрастающей, если |q| < 1, то убывающей.

и . (4.8)

Здесь S_n — сумма первых n членов прогрессии.
Упражнения

5. Вычислить все члены арифметической прогрессии с u₁ = 4 и разностью прогрессии а = 3, не превосходящие 17.

6. Вычислить сумму 10 членов геометрической прогрессии с первым членом u₁ = 3 и со знаменателем q = 4.

7. Вычислить все члены геометрической прогрессии u₁ = 2 и знаменателем прогрессии q = 2,5, не превосходящие 500.
Числовые ряды

Числовым рядом называется бесконечная последовательность чисел u₁, u₂,…,u_n соединенных знаком сложения:

.

Числа u₁, u₂,…,u_n,… называются членами ряда, а член u_n — общим или n-м членом ряда.

Ряд считается заданным, если известен его общий член u_n = f(n) (n = 1,2,...), то есть, задана функция f(n) натурального аргумента. Сумма n первых членов ряда S_n называется n-й частичной суммой ряда. Ряд называется сходящимся, если существует конечный предел последовательно­сти его частичных сумм, то есть:

.

Число S называется суммой ряда. Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся. В математике существуют специальные приемы нахождения частичных сумм ряда. Применение компьютера позволяет вычислять частичные суммы напрямую.
Упражнения

8. Найти сумму первых 7 членов ряда:

.

9. Найти сумму первых 10 членов ряда:

.

Функциональные ряды

В отличие от числовых рядов членами функционального ряда являются функции. Поэтому ряд, составленный из функций одной и той же переменной х:

,

называется функциональным. Примером функционального ряда может служить степенной ряд:

с₀ + с₁х + с₂х² + ... + с_nхⁿ + ...

Здесь числа с₀, с₁,…,с_n — коэффициенты степенного ряда.
Упражнения

10. Сумма вклада в банк 2000 руб. Банк начисляет проценты по сложной ставке 6% годовых. Определить накопленную сумму на вкладе через 7 лет.

11. Определить сумму вклада через 3 года, если процентная ставка 15% годовых и исходная сумма вклада 5000 руб.
Ряды Фурье

Важным частным случаем функциональных рядов являются ряды Фурье. Во многих задачах бывает необходимо заменить заданную периодическую функцию f(х) с периодом T точно или приближенно тригонометрической суммой 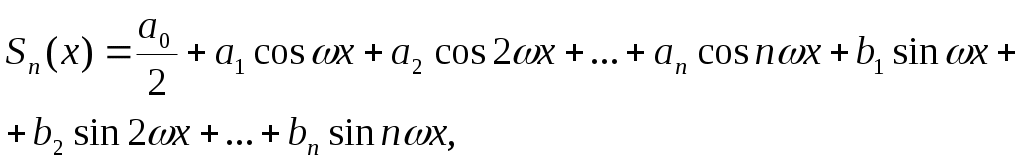(4.10):

(4.10)

где

.

Приближение (4.10) для функции f(х) будет наилучшим в смысле минимума средней квадратической ошибки:

,

если коэффициенты a_k и b_k (k = 0, 1, 2, ...) вычисляются по формулам Эйлера:

;

.

Нахождение ряда Фурье данной функции f(x) составляет задачу гармонического анализа.

Если для некоторой совокупности значений х, S_n(x) при n →∞ стремится к определенному пределу S(x), то для этих х имеем сходящийся ряд Фурье данной функции f(x). Ряд Фурье функции f(х) сходится и сумма его равна f(х) в точках непрерывности f(х), а в точках разрыва она равна

,

если функция f(x) удовлетворяет некоторым условиям, называемым условиями Дирихле. Условия Дирихле заключаются в следующем:

- интервал, на котором функция определена, может быть разбит на конечное число интервалов, в каждом из которых функция f(x) непрерывна и монотонна;

- во всякой точке разрыва f(х) существуют f(x + 0) и f(x - 0).

Непериодическая функция f(x) также может быть разложена в ряд Фурье (4.10) на промежутке 0 ≤ х ≤ l, если она удовлетворяет условиям Дирихле на этом промежутке. В этом случае

.
Упражнения

12. Получить коэффициенты а_к и b_k (k = 0,1,2,...) разложения в ряд Фурье отрезка функции у = sinjΔx, j = 0,1,2,…,31, с шагом Δx = 0,2.

13. По результатам разложения в ряд Фурье из упражнения 12 восстановить исходную функцию у = sinjΔx.
Комплексные числа

Комплексные числа используются во многих приложениях математики. Теория функций комплексной переменной является мощным инструментом при применении математических методов в различных областях научной и инженерной деятельности.
Представление комплексных чисел

Комплексным числом называется выражение вида:

z = x + iy, (4.12)

где х и у — действительные числа, i — мнимая единица.

Число х называется действительной частью числа z и обозначается Re(z), а число у — мнимой частью числа z и обозначается Im(z), то есть х = Re(z), у = Im(z).

Представление комплексного числа в виде (4.12) является алгебраической формой комплексного числа. Существуют также тригонометрическая и показательная формы.

В тригонометрической форме комплексное число может быть представлено как:

z = r(cosφ + isinφ),

а в показательной:

.

Здесь r — модуль комплексного числа z:

,

а φ — аргумент комплексного числа z:

φ = Argz = arctgy / x.

Числа z = x + iy и z = x-iy называются сопряженными.

Два комплексных числа z_l = х₁ + iy₁ и z₂ = х₂ +iy₂ называются равными, если равны их действительные и мнимые части.
Упражнения

14. Найти сопряженное комплексное число числу 2 - i5.

15. Вещественная часть комплексного числа равна 6, мнимая часть равна -2. Преобразовать в комплексное число в алгебраической форме.

16. Выделить вещественную и мнимую части комплексного числа -3 + i8.

17. Представить комплексное число z = -5 + i4 в тригонометрической форме.
Арифметические операции

На множестве комплексных чисел определены следующие арифметические операции.

1. Сумма (разность) комплексных чисел:

z₁ ± z₂ = x_l ± х₂ + i(y₁ ± у₂).

2. Произведение комплексных чисел:

z₁z₂= (x_lх₂ - y₁у₂) + i(x_ly₂ + х₂у₁).

3. Деление двух комплексных чисел:

(z₂≠0).

4. Возведение комплексного числа в натуральную степень n:

zⁿ = rⁿcosnφ + irⁿsinnφ.

5. Извлечение корня из комплексного числа:

,

где k = 0,1,2,...,n-1.
Упражнения

18. Разделить число 2 - iЗ на -2 – i.

19. Сложить комплексные числа 3 + i4, 5 - i2 и -6 + i.

20. Извлечь корень из комплексного числа 4 + i5.

21. Вычислить

.
Функции комплексной переменной

Функция ω = f(z), где z = х + iy и ω = u + iυ, определена, если известны две функции от двух действительных переменных:

u = u(х, у), υ = υ(x, у)

Из большого числа функций комплексной переменной в Excel реализованы несколько функций, наиболее часто используемых на практике. К ним относятся:

1. Экспоненциальная функция комплексной переменной

е^z - е^хе^iy = e^х (cosу + isinу),

2. Функция натурального логарифма

,

3. Функция десятичного логарифма

lgz = lg e lnz,

4, Функция логарифма по основанию 2

log₂z = log₂ е Inz,

5. Функция синуса

sinz = sinx chy + icosx shy,

6. Функция косинуса

cos z = cosx chy - isinx shy,

Здесь shy и chy — гиперболические функции синуса и косинуса соответственно:

;

.
Упражнения

22. Вычислить десятичный логарифм комплексного числа 4 - i.

23. Найти ln(2 - i2) / sin(3 + i2).

24. Вычислить sin(l + i2) cos(2 - i3).