Лекции по математической логике1. Элементы математической логики
 Скачать 2.19 Mb. Скачать 2.19 Mb.
|
Пример. Пусть требуется представить в виде таблицы следующую функцию f (x1,x2,x3)={[( | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| x1 | x2 | x3 | | | x1x2 | [ ] | x1x2 | { } | f (x1,x2,x3) |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
ВЫРАЖЕНИЕ ОДНИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ ЧЕРЕЗ ДРУГИЕ
Функция f 8(x1,x2) = x1x2 (импликация x1 в x2) может быть записана посредством функций дизъюнкции и отрицания
x1>x2=
Доказательство осуществляется посредством таблиц истинности.
| x 1 | x 2 | x1x2 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| x1 | x2 | | |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
Функцию эквивалентности f7(x1,x2)=x1x2= x1x2 выразим посредством других функций x1x2= (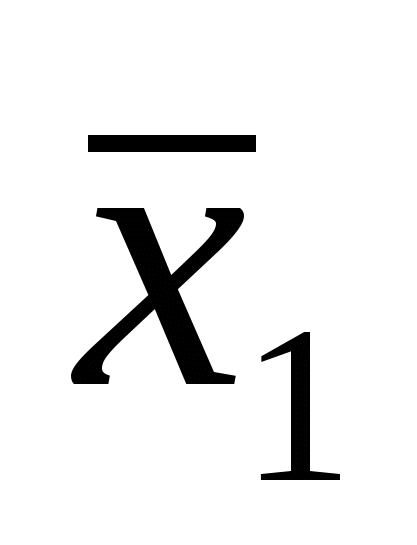 x2)&(x 1
x2)&(x 1 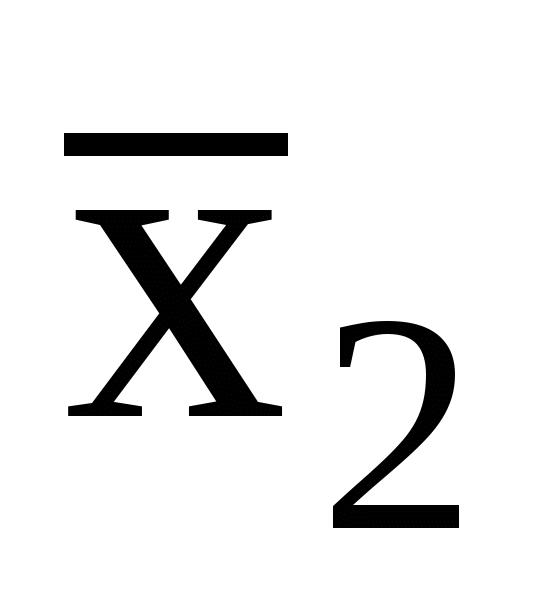 )
)
| x 1 | x 2 | x1x2 | | |||
| 0 | 0 | 1 | | |||
| 0 | 1 | 0 | | |||
| 1 | 0 | 0 | | |||
| 1 | 1 | 1 | | |||
| x 1 | x 2 | | | | x1 | ( |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
f 11(x1,x2) = x1 x2=
x2=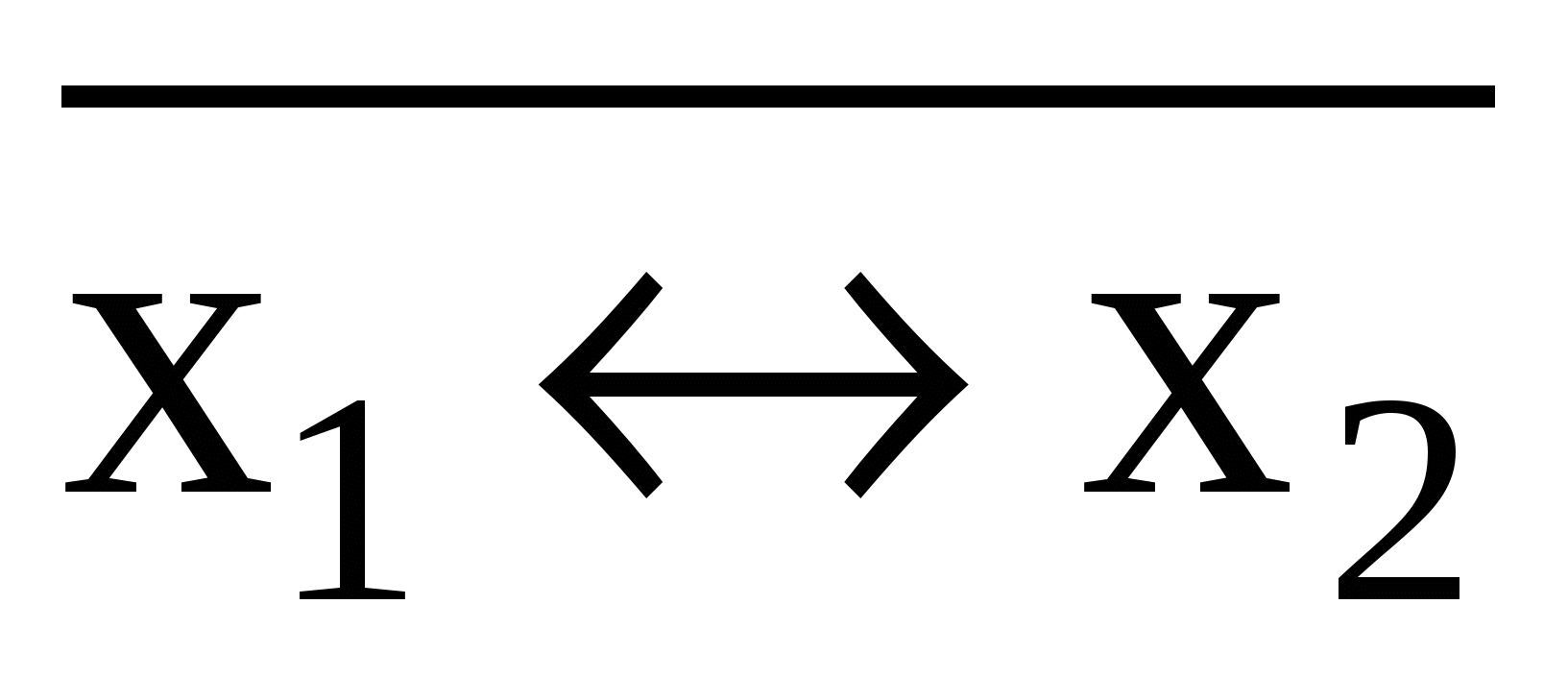
| x 1 | x 2 | x1 | x1x2 | |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
или
f(x1,x2) = x1
| x 1 | x 2 | x1 | | ( | | (x1& | ( |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
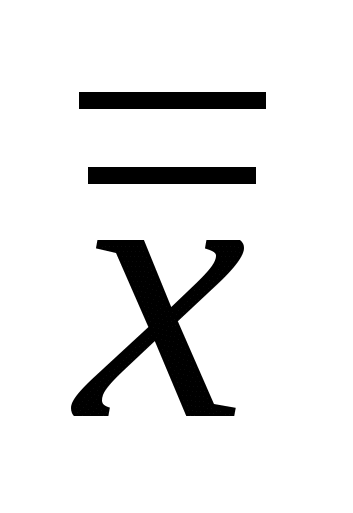 =x
=x
| x | | |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
x1& x2=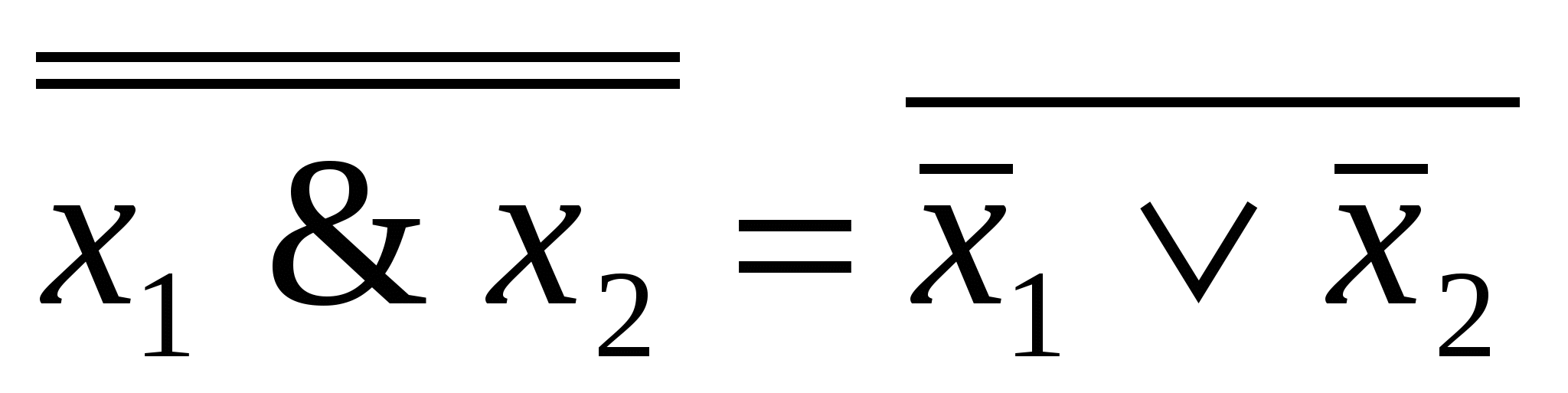
| x 1 | x 2 | x1& x2 |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| x 1 | x 2 | | | | |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 |
6. x1
| x 1 | x 2 | x1 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| x 1 | x 2 | | | | |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 |
7. x1
| x 1 | x 2 | x1 |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| x 1 | x 2 | | | | x1 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 |
Свойства конъюнкции, дизъюнкции и отрицания
Функции конъюнкции и дизъюнкции обладают рядом свойств, аналогичных свойствам обычных операций умножения и сложения. Легко убедится в том, что для этих функций выполняются сочетательный
x1&(x2&x3)= (x1&x2)&x3,
x1
переместительный
x1
x1& x2= x1&x2,
и распределительный законы. Кроме того, выполняется распределительный закон дизъюнкции относительно конъюнкции.
x1
Проверим справедливость этого закона путем сравнения таблиц для функций, стоящих в левой и правой частях рассматриваемого соотношения.
| x 1 | x 2 | x 3 | x2&x3 | x1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
| x 1 | x 2 | x 3 | x1 | x1 | (x1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
