Лекции по математической логике1. Элементы математической логики

• Название: Элементы математической логики
• Анкор: Лекции по математической логике1.doc
• Дата: 03.11.2017
• Размер: 2.19 Mb.
• Имя файла: Лекции по математической логике1.doc
• Тип: Документы; #10077
• Категория: Математика
• страница: 6 из 8

Минимальные формы

Любая булева функция представима в СН(Д или К) формах. Более того, такое представление является первым шагом перехода от табличного задания функций к ее аналитическому выражению.

В дальнейшем будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы получаются на основе принципа двойственности.

Каноническая задача синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т.е. к представлению их в дизъюнктивной нормальной форме, которая содержит наименьшее число букв (переменных и их отрицаний).

Такие формы называют минимальными.

Формула, представленная в ДНФ, упрощается многократным применением операции склеивания и операций поглощения и (дуальные тождества для конъюнктивной нормальной формы имеют вид:

).

Здесь под а и b можно понимать любую форму булевой алгебры.

В результате приходим к такому аналитическому выражению, когда дальнейшие преобразования оказываются невозможными, т.е. получаем тупиковую форму.

Среди тупиковых форм находится и минимальная ДНФ, причем она может быть неединственной. Чтобы убедиться в том, что данная тупиковая форма — минимальная, необходимо найти все тупиковые формы и сравнить их по числу входящих в них букв.

Пусть, например, функция задана в СНДФ:



Группируя члены и применяя операцию склеивания, имеем

.

При другом способе группировки получим:

.

Обе тупиковые формы не являются минимальными. Чтобы получить минимальную форму, нужно догадаться повторить в исходной формуле один член (это всегда можно сделать, т.к. ).

В первом случае таким членом может быть . Тогда

.

Добавляя член , получим:

.

Перебрав все возможные варианты, можно убедиться, что две последние формы минимальны.

Работа на таком уровне подобна блужданию. Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать графические и аналитические представления.

Метод неопределенных коэффициентов

Метод применим для минимизации функций алгебры логики от любого числа переменных.

Рассмотрим случай трех переменных. Булева функция в ДНФ может быть представлена в виде всевозможных конъюнктивных членов, которые могут входить в ДНФ: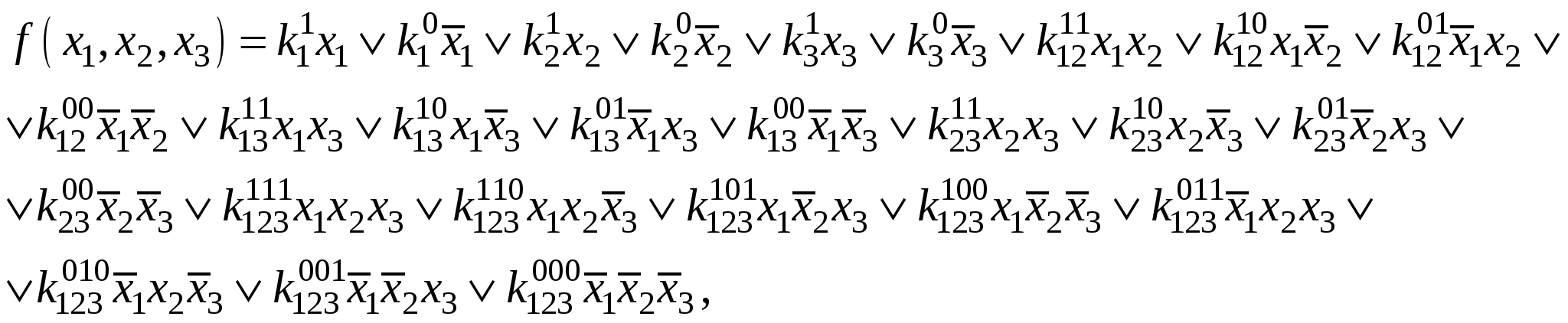



где kÎ{0,1}   коэффициенты. Метод заключается в подборе коэффициентов таким образом, чтобы получаемая ДНФ была минимальной.

Если теперь задать всевозможные значения переменных от 000 до 111, то получим 2ⁿ (2³ =8) уравнений для определения коэффициентов k:

;

;

;

;

;

;

;

.

Рассматривая наборы, на которых функция принимает нулевое значение, определяют коэффициенты, которые равны 0, и вычеркивают их из уравнений, в правой части которых стоит 1. Из оставшихся коэффициентов в каждом уравнении к единице приравнивают по одному коэффициенту, определяющему конъюнкцию наименьшего ранга. Остальные коэффициенты приравнивают к 0. Итак, единичные коэффициенты k определяют соответствующую минимальную форму.

Пример. Минимизировать заданную функцию

,

если известны значения: ; ; ; ; ; ; ; .

_{Решение.}

=1;

=0;

=0;

=0;

=1;

=1;

=1;

=1.

После вычеркивания нулевых коэффициентов получим:

=1;

=1;

=1;

=1;

=1.

Приравняем к единице коэффициент , соответствующий конъюнкции наименьшего ранга и обращающий четыре последних уравнения в 1, а в первом уравнении целесообразно приравнять к 1 коэффициент . Остальные коэффициенты приравнивают к 0.

Ответ: вид минимизированной функции .

Следует отметить, что метод неопределенных коэффициентов эффективен, когда число переменных невелико и не превышает 5-6.
Многомерный куб

Рассмотрим графическое представление функции в виде многомерного куба. Каждой вершине n-мерного куба можно поставить в соответствие конституенту единицы.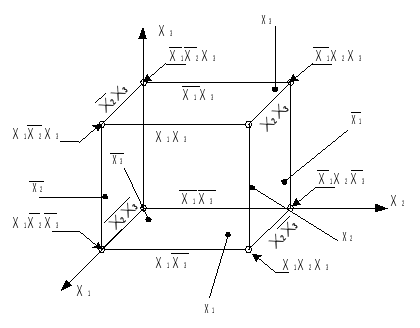



Подмножество отмеченных вершин является отображением на n-мерном кубе булевой функции от n переменных в СДНФ.

Для отображения функции от n переменных, представленной в любой ДНФ, необходимо установить соответствие между ее минитермами и элементами n-мерного куба.

Минитерм (n-1)-го ранга можно рассматривать как результат склеивания двух минитермов n-го ранга, т.е.

=

На n-мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координат х_i, соединяющих эти вершины ребром (говорят, что ребро покрывает инцидентные ему вершины).

Таким образом, минитермам (n-1)-го порядка соответствуют ребра n-мерного куба.

Аналогично устанавливается соответствие минитермов (n-2)-го порядка граням n-мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).

Элементы n-мерного куба, характеризующиеся S измерениями, называются S-кубами.

Так вершины являются 0-кубами, ребра 1-кубами, грани 2-кубами и т.д.

Обобщая, можно сказать, что минитерм (n-S) ранга в ДНФ для функции n переменных отображается S-кубом, причем каждый S-куб покрывает все те кубы низшей размерности, которые связаны только с его вершинами.

Пример. На рис. дано отображение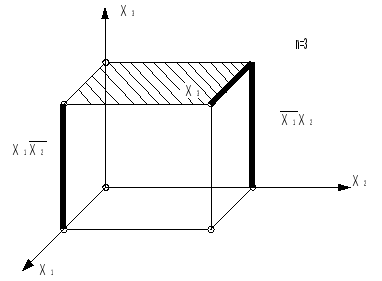



Здесь минитермы и соответствуют 1-кубам (S=3-2=1), а минитерм х₃ отображается 2-кубам (S=3-1=2).

Итак, любая ДНФ отображается на n-мерном кубе совокупностью S-кубов, которые покрывают все вершины, соответствующие конституентам единицам (0-куба).

Конституенты. Для переменных х₁, х₂,… х_n выражение называют конституентой единицы, а — конституентой нуля ( означает либо , либо ).

Данная конституента единицы (нуля) обращается в единицу (нуль) только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными единице (нулю), а их отрицания — нулю (единице).

Например: конституенте единице соответствует набор (1011), а конституенте нуля — набор (1001).

Так как СД(К)НФ является дизъюнкцией (конъюнкцией) конституент единицы (нуля), то можно утверждать, что представляемая ею булева функция f(x₁,x₂,…,x_n) обращается в единицу (нуль) только при наборах значений переменных x₁,x₂,…,x_n, соответствующих этим копституантам. На остальных наборах эта функция обращается в 0 (единицу).

Справедливо и обратное утверждение, на котором основан способ представления в виде формулы любой булевой функции, заданной таблицей.

Для этого необходимо записать дизъюнкции (конъюнкции) конституент единицы (нуля), соответствующих наборам значений переменных, на которых функция принимает значение, равное единице (нулю).

Например, функции, заданной таблицей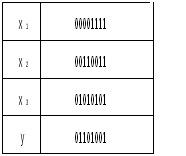



соответствуют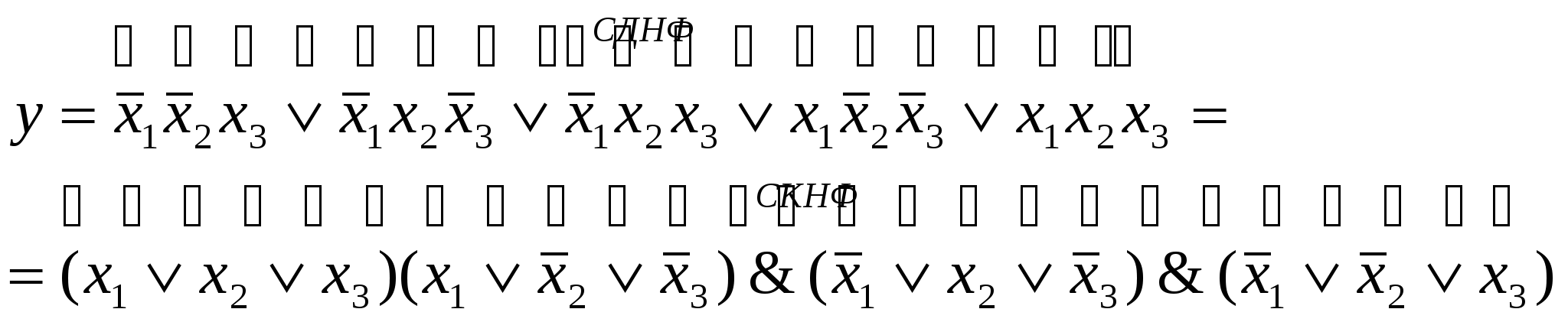



Полученные выражения можно преобразовать к другому виду на основании свойств алгебры логики.

Справедливо и обратное утверждение: если некоторая совокупность S-кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим S-кубам минитермов является выражением данной функции в ДНФ.

Говорят, что такая совокупность S-кубов (или соответствующих им минитермов) образует покрытие функции. Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число S-кубов которого было бы поменьше, а их размерность S — побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием.

Например, для функции у= покрытие соответствует неминимальной форме:

рис a) у=,

а покрытия на рис б) у=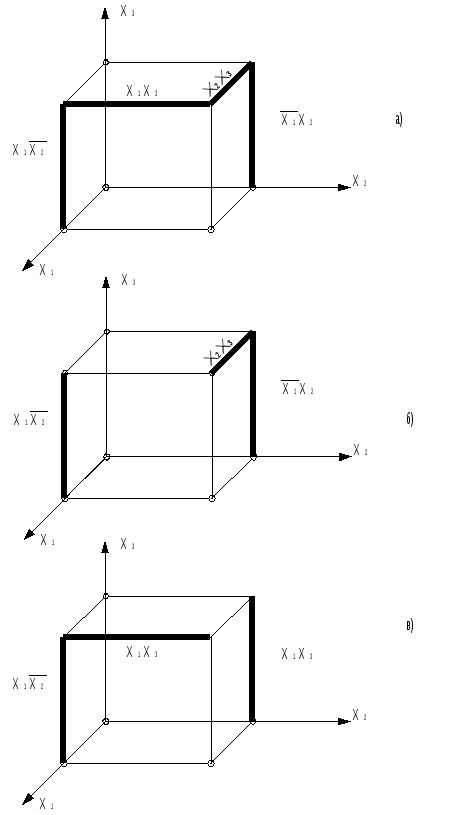, рис в) у= минимальные.


Рис. Покрытие функции у=:

а) неминимальное; б), в) минимальное.
Отображение функции на n-мерном наглядно и просто при n3. Четырехмерный куб можно изобразить, как показано на рис., где отображены функции четырех переменных и ее минимальное покрытие, соответствующее выражению у=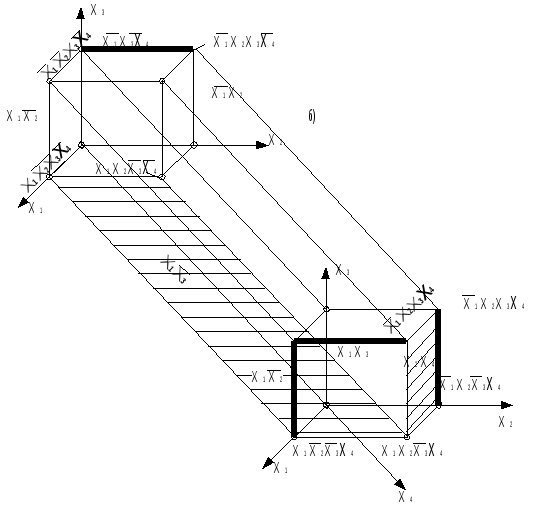



Использование этого метода при n>4 требует настолько сложных построений, что теряет все его преимущества.
Карты Карно

В другом методе графического отображения булевых функций используют карты Карно — специально организованные таблицы соответствия.

Столбцы и строки таблицы соответствуют всевозможным наборам значений не более 2-х переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством.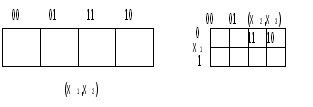



Рис. Карты Карно для 2-х и 3-х переменных.
Карты Карно для 4-х переменных.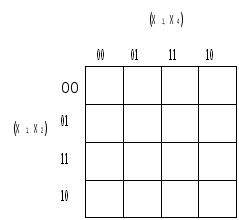



Как и в обычных таблицах соответствия клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписываются, им соответствуют пустые клетки).

Например, на рис. показана карта Карно для функции, отображение которой дано на 4-х-мерном кубе (см. рис.).

Для упрощения строки и столбцы, соответствующие значениям “1” для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.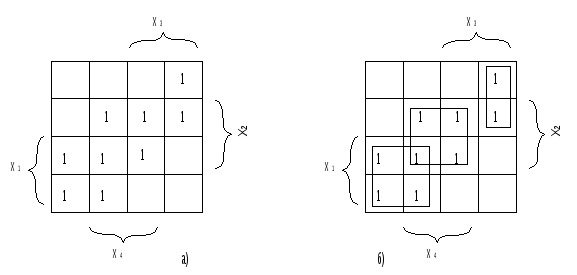



Рис. а) отображение функции четырех переменных;

б) отображение ее минимального покрытия.
Между отображениями функции на n-мерном кубе и на карте Карно имеет место взаимно-однозначное соответствие. На карте Карно S-кубу соответствует совокупность 2-х соседних клеток, размещенных в строке, столбце, квадрате или прямоугольнике. Поэтому все положения, изложенные ранее, справедливы и для карт Карно. Так на рис. б) показано покрытие единиц карты, соответствующее минимальной дизъюнктивной форме

у=, рассматриваемой функции.

Считывание минитермов с карты Карно осуществляется по простому правилу. Клетки, образующие S-куб, дают минитерм (n-S)-го ранга, в который входят те (n-S)-переменные, которые сохраняют одинаковые значения на этом S-кубе, причем значениям “1” соответствуют сами переменные, а значениям “0” их отрицание.

Переменные, которые не сохраняют свои значения на S-кубе, в минитерме отсутствуют. Различные способы считывания приводят к различным представлениям функции в ДНФ.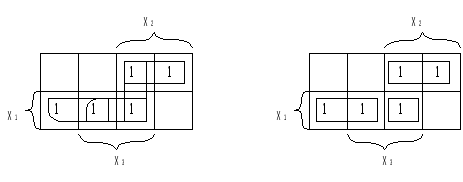



у= у=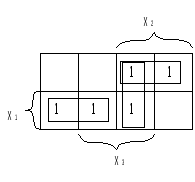



у=

Использование карт Карно требует более простых построений по сравнению с отображением на n-мерном кубе, особенно в случае 4-х переменных.

Для отображения функций 5-ти переменных используют две карты Карно на 4-ре переменные, а для функции 6-ти переменных — четыре таких карты.

При дальнейшем увеличении числа переменных карты Карно становятся практически непригодны.
Метод Мак-Класски (алгебраический метод)

Алгебраический метод известен как метод Мак-Класски, модифицировавшего в 1956 году метод Квайна. Базируется данный метод на следующей теореме.

Теорема. Если в СДНФ функции алгебры логики произвести всевозможные операции неполного склеивания, а затем всевозможные операции элементарного поглощения, то полученная форма функции будет сокращенной.

Элементарную конъюнкцию ранга n будем называть минитермом ранга n.

Элементарная конъюнкция называется импликантой булевой функции , если , то есть булева функция на данном наборе является константной и равна 1.

Минимизация булевой функции по методу Мак-Класски осуществляется согласно следующей последовательности действий:

1. Записать минитермы в виде их двоичных кодов и разбить их на непересекающиеся группы по числу единиц в этих группах. В i-ю группу войдут только те кодовые комбинации, которые в своей двоичной записи содержат ровно i единиц. Группы располагаются по мере роста i.

2. Попарное сравнение минитермов.

2.1. Произвести попарное сравнение двоичных номеров всех членов группы с индексом i с членами только группы с индексом (i+1).

2.2. Если некоторые два минитерма имеют вид ax_i и , то выписывают конъюнкцию а, которая является минитермом ранга (n-1), то есть если сравниваемы двоичные коды различаются только в одном разряде, то в столбец остатков записывается двоичный код с прочерком “-” на месте этого разряда (этот код соответствует минитерму (n-1)-го ранга.

2.3. Все двоичные коды номеров, участвующих в операции сравнения при условии их склеивания, отмечаются знаком “*”.

2.4. Пункты 2.1-2.3. повторяются для всех групп последовательно в порядке возрастания i. Двоичные коды, не отмеченные знаком “*”, соответствуют простым импликантам.

2.5. После построения всех минитермов (n-1) ранга по пунктам 2.1-2.3, они также сравниваются между собой и получают минитермы ранга (n-2) и т.д. Работа по первому этапу продолжается до тех пор, пока среди двоичных кодов можно будет обнаружить сравнимые, то есть такие укороченные коды, которые содержат прочерки в одних и тех же разрядах и различаются значением одного разряда.

Все неотмеченные минитермы называются первичными или простыми импликантами.

3. Построение импликантной таблицы. Строится таблица, в которой число строк равно числу полученных первичных импликант минимизируемой функции, а число столбцов равно числу минитермов исходной СДНФ. Если в некоторый минитерм исходной СДНФ входит первичная импликанта, то на пересечении строки и столбца ставится метка. Данные импликантной таблицы позволяют определить импликанты, отбросив которые, истинность функции не изменится.

4. Нахождение существенных импликант. Если в каком-либо из столбцов полученной таблицы имеется только одна метка, то первичная импликанта, стоящая в соответствующей строке, называется существенной. Существенная импликанта включается в минимальную ДНФ, а из таблицы исключаются строки, соответствующие существенным импликантам, а также столбцы минитермов, покрываемые этими существенными импликантами. Если в таблице нет столбцов, содержащих только одну метку, то переход на п.7.

5. Вычеркивание лишних столбцов. Если в таблице после четвертого этапа есть два столбца, в которых стоят метки в одинаковых строках, то один из них вычеркивают, так как покрытие оставшегося столбца будет осуществлять покрытие исключенного минитерма.

6. Вычеркивание лишних первичных импликант. Если на пятом этапе появляются строки, в которых нет меток, то первичная импликанта исключается из дальнейшего рассмотрения.

7. Выбор минимального покрытия. Выбирают наименьшее число строк таких, чтобы для каждого столбца из данной таблицы и каждой метки в этом столбце нашлась бы по крайней мере одна строка из множества выбранных строк, которая содержит эту метку.

Дизъюнкция всех простых импликантов покрытия, в том числе и существенных, образует тупиковую форму функции. Из найденных тупиковых форм выбирают минимальную по наименьшему числу дизъюнкций и элементов переменных.

Пример.

.

1) Получение групп кодовых комбинаций. 0011 0100 0101 0111 1001 1011 1100 1101

1 гр. 0100 2 гр. 0011 3 гр. 0111

0101 1011

1001 1101

1100

2) Попарное сравнение минитермов.

Минитермы 3-го ранга: 010-*, -100, 0-11, -011, -101, 10-1, 1-01, 110-*

Минитермы 2-го ранга: -10-.
3) Построение импликантной таблицы и расстановка меток

	0100	0011	0101	1001	1100	0111	1011	1101
-100	*				*
0-11		*				*
-011		*					*
-101			*					*
10-1				*			*
1-01				*				*
-10-	*		*		*			*

4) Нахождение существенных импликант. Столбец, соответствующий кодовой комбинации 0111 содержит единственную метку. Соответствующая этой метке импликанта является существенной, поэтому включаем ее в минимальную ДНФ , а из таблицы согласно п.4 исключаем столбцы и строку, после чего получаем следующую таблицу:

	0100	0101	1001	1100	1011	1101
-100	*			*
-011					*
-101		*				*
10-1			*		*
1-01			*			*
-10-	*	*		*		*

5) и 6) В полученной таблице нет столбцов, в которых стоят метки в одинаковых строках и нет строк, в которых нет меток, поэтому переходим к п.7.

7) Выбор минимального покрытия. Минимальному покрытию соответствует выбор строк -10- и 10-1. Тогда минимизированная ДНФ запишется как .