Лекции по математической логике1. Элементы математической логики
 Скачать 2.19 Mb.
|
|
Совпадение построенных таблиц доказывает наше утверждение. Рассмотрим теперь ряд простых, но весьма важных соотношений 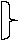 х х=х;х&х=х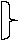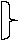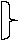. х 1=1; х0=х; х =1;х&1=х. х&0=0. х& =0. И как следствие получаем х х…х=х,х&х&…&х=х. Как обобщение формул получаем следующие формулы, называемые формулами (законами) де Моргана х1 х2…хn= ;х1&х2&…&хn=  .Свойства функций сложения по модулю 2, импликации, штриха Шеффера и стрелки Пирса (функции Вебба) Свойства функции сложения по модулю 2 и функции импликации часто бывают полезными при анализе и синтезе различных дискретных устройств. Для функции сложения по модулю 2 выполняются переместительный и сочетательный законы, а также распределительный закон относительно конъюнкции: x1  x2= x2 x1;x1 (x2x3)= (x1x2)x3;x1&(x2 x3)= (x1&x2)( x1&x3).Справедливы также очевидные соотношения  xx=0;x 0=х;x 1=;х =1.Кроме того, выполняется формула х1 х2= x1x2 x1&x2.В отличие от всех ранее рассмотренных функций для импликации не выполняются переместительный и сочетательный законы, однако справедливы следующие соотношения: х  x=1;x =;x1=1; х0= ;0х=1; 1х=х; х1х2=  ;х1х2 х1= х1. Функции дизъюнкции и конъюнкции могут быть выражены через импликацию следующим образом: х1х2= х2;х1&х2=  .Для функции Шеффера и Вебба справедлив переместительный закон: х1 /х2= х2/х1; х1х2= х2х1. Сочетательный закон для них не выполняется: х1/(х2/х3)(х1/х2)/х3 ; х1( х2х3) (х1 х2) х3. С  праведливы следующие очевидные соотношения, проверка которых аналогична приведенным выше примерам и осуществляется при помощи таблиц истинности:х/х= , х х=;х/ =1, х=0;х/1= , х1 =0;х/0=1, х0= ;х1/х2=  = ;х1х2=  =&.Функции Шеффера и Вебба связаны между собой соотношениями, аналогичными формулами де Моргана для функций конъюнкции и дизъюнкции: х1/х2= ;х1х2=  .ОСНОВНЫЕ КЛАССЫ ФАЛ В качестве первого класса таких ФАЛ рассмотрим класс функций, сохраняющих константу нуль, т.е. таких функций, для которых справедливо равенство f (0, 0, …, 0)=0 Очевидно, что в фиксированном множестве число функций этого класса составляет половину всех функций алгебры логики, т.е.  функций.Аналогично класс функций, сохраняющих константу единица, будет определен, как класс функций, для которых выполняется равенство f (1, 1,…, 1)=1 Этот класс состоит также из функций.Определение Функция f*(x1 ,…,xn) называется двойственной к функции f(x1 ,…,xn), если выполняется равенство f*(x1 ,…,xn)=  .Определение Функция .f(x1 ,…,xn) самодвойственный, если она совпадает с двойственной себе функцией, т.е. справедливо равенство f(x1 ,…,xn )= .Определение ФАЛ f(x1,…,xn ) называется линейной, если она представима в следующем виде f(x1 ,…,xn )=с0 с1х1… сnхn,где коэффициент сi  {0, 1}.Число членов этого класса  .Определение ФАЛ f(x1,…,xn ) называется монотонной, если для любых двух наборов Х1 и Х2 таких, что Х1 Х2выполняется равенство f(X1)f(X2) X1=<  >X2=<  >.Определение ФАЛ f(x1,…,xn ) называется симметричной, если она не изменяется при произвольной перенумерации аргументов. f(x1,…,xn )= f(y1,…,yn ), где (y1,…,yn) – любая перестановка аргументов (x1,…,xn ). АНАЛИТИЧЕСКАЯ ЗАПИСЬ ФАЛ Пусть имеется двоичный набор <  >. Сопоставим ему число i, определяемое i=  + +…+ ,число i называют номером набора < >.Рассмотрим функцию F(x1,…,xn), определяемую следующим соотношением  1, если номер набора i(0) Fi= 0, в противном случае. Такую функцию называют характеристической функцией «единицы». Предположим, что удалось построить аналитическое выражение для функции Fi (как это можно сделать описывается ниже). Тогда справедлива следующая теорема. Теорема. Любая таблично заданная функция ФАЛ может быть задана в следующей аналитической форме (1) f(x1,…,xn )=   … = ,где Ti – множество номеров наборов, на которых функция обращается в единицу. Справедливость этой теоремы вытекает из следующего. Возьмем произвольный набор аргументов из таблицы, задающей функцию. Возможны два случая:
В  силу х1=1х •1 = 1 х 0=хх&0 =0 х  =1х • =0.при этом вся правая часть (1) будет также равна единице. Если же на рассматриваемом наборе функция f(x1,…,xn )=0, то как следует из формулировки теоремы, среди характеристических функций  не будет такой, у которой индекс совпадает с номером рассматриваемого набора аргументов. Все члены дизъюнкции будут равны 0 в правой части. Мы доказали, что левая и правая часть соотношения (1) совпадают на любом наборе.2. В теореме (1) мы воспользовались дизъюнкцией характеристических функций. Выясним, нельзя ли вместо дизъюнкции использовать какую-либо другую ФАЛ. Для того, чтобы выполнялось соотношение, подобное (1), необходимо, чтобы при обращении любой из характеристических функций в «1» все выражение обращалось в «1», а при нулевых значениях (0) все выражение становилось равным 0. Если обозначить неизвестную операцию значком  , то сформулированное нами условие представимо в виде таблицы.
|