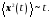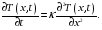шаблон. Элементы нейронного контроля
 Скачать 49.48 Kb. Скачать 49.48 Kb.
|
Глава 4 Элементы нейронного контроляНейронный контроль является ветвью общего поля интеллектуального управления, которая основана на концепции искусственного интеллекта (ИИ). ИИ можно определить как компьютерную эмуляцию процесса мышления человека. Методы искусственного интеллекта обычно классифицируются на экспертные системы (ES), нечеткая логика (FL) и искусственные нейронные сети (ANN). Классические экспертные системы основаны на булевой алгебре и используют точные вычисления в то время, как системы нечеткой логики включают расчеты, основанные на приблизительных рассуждениях. Нечеткая логика является обычной (булевой) логикой, которая была расширена для обработки концепции частичной истины - истины между «полностью истинным» и «совершенно ложным» [88]. Это понятие было введено доктором Лотфи Заде из Калифорнийского университета в Беркли в 1960-х годах, как средство моделирования неопределенности естественного языка. Истина логического выражения в нечеткой логике — это число в интервале [0,1]. Нечеткая логика возникла как прибыльный инструмент для управления сложными промышленными процессами и системами. Она используется для процессов, которые не имеют простых математических моделей, для сильно нелинейных процессов, или где обработка лингвистически сформулированного знания должна быть выполнена. Хотя она была открыта в Соединенных Штатах, быстрый рост этой технологии произошел из Японии и теперь снова достиг США и Европа. Контроллеры, основанные на этом математическом подходе, известны как нечеткие контроллеры. Использование искусственных нейронных сетей (ИНС) является наиболее мощным подходом в ИИ. ИНС - это структуры обработки информации, которые имитируют архитектуру и режим биологической нервной ткани. Любая ИНС - это система, состоящая из нескольких основных объектов (называемые нейронами), которые взаимосвязаны и работают в параллельной передаче сигналов друг другу для достижения определенной задачи обработки [237]. Один из наиболее выдающихся особенностей ИНС является их способность моделировать процесс обучения. Они снабжены парами входных и выходных сигналов, из которых общие правила автоматически выводится так, что ИНС будет (при определенных условиях) способна генерировать правильный выход для сигнала, который ранее не использовался. Нейронный подход может быть совмещен с нечеткой логикой, производя нервно-нечеткие системы, которые совмещают преимущества из двух контрольных парадигм. 4.1 Типы нейронов Работа искусственных нейронов основана на своих природных аналогах. Каждый искусственный нейрон имеет несколько входов (соответствующих синапсам биологического нейронов) и один-единственный выход, аксон. Каждый входной сигнал охарактеризован некоторым весом, указывающим на влияние соответствующего сигнала на выход нейрона. Нейроны вычисляют эквивалентный суммарный входной сигнал как взвешенную сумму индивидуальных входных сигналов (4.1). (net =i=1n wi ⋅ xi) (4.1) Затем полученное количество сравнивается с постоянным значением,называемым порогом.Уровень и выходной сигнал рассчитывается как функция их разности (нетто - т). Это функция называется передаточной функцией или функцией активации. Веса ввода, пороговый уровень и функция активации являются параметрами, которые полностью описывают искусственный нейрон. В зависимости от типа искусственного нейрона активация функция может иметь несколько форм. Есть аналоговые нейроны с использованием непрерывного реального функции активации и дискретные нейроны, чьи функции активации являются прерывистыми. Биполярные нейроны генерируют как положительные, так и отрицательные выходы, в то время как однополярные только положительные значения. В случае биполярных аналоговых нейронов наиболее популярна активация функция дается формулой (4.2). Выход непрерывно изменяется от –1 до 1, в зависимости от входных сигналов, которые могут иметь любое реальное значение (рис. 4.1). Рисунок 4.1 – Sigmoidal activation function of bipolar analogue neurons(L=1) Параметр λ - это константа, управляющая наклоном графика функции активации. Некоторые авторы считают, что λ = 1, чтобы упростить вычисления, в то время как другие работают с более общим форматом представленным в (4.2), но основные результаты и свойства соответствующие ANN остаются действительными в обеих ситуациях. Функция в (4.2) является частью больший класс передаточных функций, называемый «сигмоидальными функциями». Что у них общего это форма графика и свойство, которое должно быть выводимым, что важно в некоторых приложениях. (net =i=1n wi ⋅ xi) (4.2) Альтернативная функция активации представлена в (4.3). Это часть сигмоидальной функции группы и, как показано в (4.4), она имеет те же предельные значения, что и функция f1. Униполярные аналоговые нейроны похожи на биполярные с той разницей, что выходные сигналы могут принимать значения только от 0 до +1 (рис. 4.2). Их функция активации описывается формулой (4.5). (net =i=1n wi ⋅ xi) (4.2) Рисунок 4.1 – Sigmoidal activation function of unipolar analogue neurons (λ=1) (net =i=1n wi ⋅ xi) (4.2) (net =i=1n wi ⋅ xi) (4.2) Не все функции непрерывной активации являются сигмоидальными. Пошагово-линейная активация функция, представленная в (4.6), не выводима в двух точках: net = t - 1.0 и net = t + 1.0 (Рис. 4.3). Рисунок 4.1 – Non-sigmoidal activation function (net =i=1n wi ⋅ xi) (4.2) Дискретные нейроны используют функции активации порогового типа. Биполярный дискретный сорт связан с функцией активации, описанной в (4.7), в то время как однополярный тип использует функция активации, иллюстрируемая (4.8). Эти две функции можно считать ограничивающими (λ→∞) в (4.2) и (4.5). (net =i=1n wi ⋅ xi) (4.2) (net =i=1n wi ⋅ xi) (4.2) За последние несколько лет более сложные типы нейронов и функции активации были введены для решения различных видов практических задач. Особенно, радиальные нейроны оказались очень полезными для многих систем управления и систем идентификационные приложения. Эти нейроны используют так называемые функции активации радиальной основы. Уравнение (4.9) представляет собой наиболее часто используемую форму для такой функции, где ‘x’ – двумерный вектор входных сигналов и «т» постоянный вектор того же размера в то время, как || · || является евклидовой нормой в n-мерном пространстве. (net =i=1n wi ⋅ xi) (4.2) Практически f7 показывает, насколько близок вектор "x" к вектору "t" в этом n-мерном пространстве. Чем ближе x к t, тем больше f7 (x); если x = t, то f7 (x) = 1. Классический гауссовский колокол, полученный для одномерного случая, в то время как двумерный случай иллюстрируется в Рис. 4.4. Очевидно, что такой тип нейронов очень далек от биологической модели, но это не имеет значения, поскольку он оказывается полезным для определенных технических приложений. Рисунок 4.1 – Radial basis activation function: two-dimensional case 4.2 Искусственные нейронные сети 1. Частицы движутся из областей более высоких концентраций к областям более низких концентраций. 2. Функция плотности вероятности концентрации имеет гауссово распределение. 3. Асимптотическое среднеквадратическое смещение является линейной функцией времени, т. е.
4. Диффузия наблюдается в системах, близких к равновесию. 5. Распределение скоростей частиц – максвелловское. Размеры системных матриц определяются в соответствии с числом состояний входов и выходов следующей программы: [m1,n1]=size(Cd); [n1,n_in]=size(Bd); A_e=eye(n1+m1,n1+m1); A_e(1:n1,1:n1)=Ad; A_e(n1+1:n1+m1,1:n1)=Cd*Ad; B_e=zeros(n1+m1,n_in); B_e(1:n1,:)=Bd; B_e(n1+1:n1+m1,:)=Cd*Вd; C_zeros(m1,n1+m1); C_e(:,n1+1:n1+m1)=eye(m1,m1); Модель нормальной диффузий математически описывается уравнением диффузии вида
Однако существуют классы систем (2.), не соответствующих вышеупомянутым свойствам и функциям. 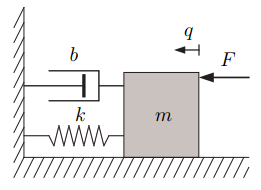 Рисунок 2.1 – Example of a mechanical passive system Примерами таких систем являются [210]: перенос дырок и электронов (2.) внутри аморфных полупроводников под действием электрического поля, перемещение загрязняющих веществ в подземных водах, диффузия белков через клеточные мембраны, движение больших молекул и металлических кластеров на кристаллических поверхностях, полет альбатроса, движение частиц внутри быстро вращающегося кольцевого резервуара, процессы, протекающие в композитных материалах на основе графена, и многие другие. Это системы, состояние которых находится далеко от равновесного. |