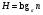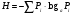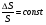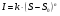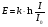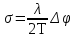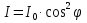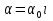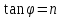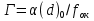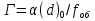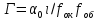|
|
Элементы теории вероятностей
ВОПРОСЫ И ЗАДАЧИ К МОДУЛЮ «ОСНОВЫ БИОЛОГИЧЕСКОЙ ФИЗИКИ»ДЛЯ СТУДЕНТОВ 1 КУРСА ВСЕХ ФАКУЛЬТЕТОВ на 1 семестрТЕМА: Элементы теории вероятностей.Теоретические вопросы
Сформулируйте определение события с точки зрения теории вероятностей.
* Pезультат испытаний
Что называют абсолютной частотой случайного события?
* Предел, к которому стремится относительная частота события при числе опытов, стремящихся к бесконечности
Что называют относительной частотой событий?
* Отношение общего числа опытов к числу испытаний, которые благоприятствуют наступлению интересующего события
Дайте определение случайного события.
* Которое может произойти, но может и не произойти в результате данного опыта
Дайте определение достоверного события.
* Которое обязательно наступит в результате испытания
Дайте определение невозможного события.
* Никогда не может произойти в результате данного опыта
Чему равна вероятность достоверного события?
*1
Чему равна вероятность невозможного события?
*0
Какие события называются совместными?
* Которые могут наступать одновременно в результате данного испытания.
Какие события называются несовместными?
* Которые никогда не могут наступать одновременно в результате данного опыта
Какие события называются зависимыми?
* Зависимыми называются события А и В, если вероятность наступления события В изменяется в зависимости от того, произошло ли событие А
Какие события называются независимыми?
* Независимыми называются события А и В, если вероятность наступления события В не изменяется в зависимости от того, произошло ли событие А
Какие события называются противоположными?
* Под противоположным событием понимается событие Ā, которое обязательно должно произойти, если не наступило некоторое событие А
Чему равна сумма вероятностей противоположных событий?
*0
Какие события образуют полную группу несовместных событий?
* Которые несовместны и в результате каждого испытания появляется только одно из этих событий
Чему равна сумма вероятностей событий, которые образуют полную группу событий?
*1
Сформулируйте классическое определение вероятности случайного события.
* Отношение благоприятствующих случаев к общему числу равновозможных совместных событий
Сформулируйте статистическое определение вероятности случайного события.
* Предел, к которому стремится относительная частота встречаемости событий при неограниченном увеличении числа испытаний
Дайте определение условной вероятности
* События В при условии, что событие А состоялось
Как записывается формула теоремы сложения вероятностей?
* Р (А или В)=Р(А)+Р(В)
Сформулируйте теорему сложения вероятностей.
* Вероятность появления одного из нескольких несовместных событий (А или В) равна Р(А)+Р(В)
В каких случаях применяется теорема сложения вероятностей?
* Когда необходимо рассчитать вероятность одновременного появления нескольких независимых событий 23. Сформулируйте теорему умножения вероятностей для независимых событий. * Вероятность одновременного появления в результате опыта двух и более независимых событий равна произведению вероятностей этих событий 24. Как записывается формула теоремы умножения вероятностей для независимых событий? * Р (А и В)=Р(А)*Р(В) 25. В каких случаях применяется теорема умножения вероятностей для независимых событий? * Когда требуется вычеслить вероятность одновременного появления нескольких независимых событий 26. Сформулируйте теорему умножения вероятностей для зависимых событий. * Вероятность совместного появления в результате опыта двух (или более) зависимых событий равна произведению вероятности первого события на условную вероятность второго (третьего и т.д.)
Сформулируйте теорему умножения вероятностей для независимых событий.
* Вероятность одновременного появления в результате опыта двух и более независимых событий равна произведению вероятностей этих событий
В каких случаях применяется теорема умножения вероятностей для независимых событий?
* Когда требуется вычислить вероятность одновременного появления нескольких независимых событий
Как записывается формула теоремы умножения вероятностей для зависимых событий?
* Р (А и В)=Р(В)*Р(А/В)
В каких случаях применяется теорема умножения вероятностей для зависимых событий?
* Когда необходимо рассчитать вероятность одновременного появления нескольких зависимых событий
Как записывается формула теоремы полной вероятности?
* 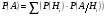
В каких случаях применяется формула полной вероятности?
* Когда событие А наст только при усл появления одного из событий образующих полн группу
В каких случаях применяется формула Байеса?
* Когда событие А появляющееся совместно с каким-либо из событий образующих полную группу произошло и требуется произвести количественную переоценку вероятностей гипотез В 1, В 2, В n. ТЕМА: Элементы теории вероятностейЗадачи
Из 900 больных, поступивших в хирургическое отделение больницы, 150 человек имели травмы. Какова относительная частота поступления травмированных больных? (Ответ: 0,17.)
В институт было подано 1250 заявлений о приеме от девушек и 1050 - от юношей. Какова относительная частота подачи заявлений от девушек? (Ответ: 0,54)
Грани правильного тетраэдра пронумерованы: 1,2,3,4. Какова вероятность того, что при бросании тетраэдр станет на грань с цифрой 2? Предполагается, что тетраэдр сделан из однородного материала. (Ответ: 0,25)
Студент подготовил к экзамену 25 билетов из 40. Какова вероятность того, что он "вытащит" выученный билет? (Ответ: 0,625)
В урне находится 10 шаров: 3 белых, 5 черных и 2 красных. Из урны извлекается черный шар и в урну не возвращается. Какова вероятность извлечь после этого черный шар? (Ответ: 0,44)
В коробке находятся 5 синих, 10 черных и 15 красных карандашей. Какова вероятность того, что первый наугад вынутый карандаш окажется синим или красным? (Ответ: 0,67)
Стрелок стреляет по мишени, имеющей 3 области. Вероятность попасть в первую область равна 0,3, вероятности попасть во вторую и третью области равны, соответственно, 0,25 и 0,45. Найти вероятность того, что, выстрелив один раз, стрелок попадет в первую или во вторую область. (Ответ: 0,55)
Вероятность того, что день будет дождливым, равна 0,6. Найти вероятность того, что день будет ясным. (Ответ: 0,4)
Три врача независимо друг от друга осмотрели одного и того же больного. Вероятность того, что первый врач установит верный диагноз, равна 0,8. Для второго и третьего врачей эти вероятности соответственно, равны 0,7 и 0,9. Определить вероятность того, что все врачи поставят правильный диагноз. (Ответ: 0,5)
Два врача независимо друг от друга осмотрели одного и того же больного. Вероятность того, что первый врач установит верный диагноз, равна 0,8. Для второго врача эта вероятность равна 0,7. Определить вероятность того, что оба врача поставят ошибочный диагноз. (Ответ: 0,06)
Дальтоник воспринимает красный и зеленый цвет как серый. В корзине находятся два красных, 4 зеленых, 2 белых и 2 черных шара. Какова вероятность того, что наугад вытянутый дальтоником шар окажется для него "серым"? (Ответ: 0,6)
На приеме у врача находятся 15 больных. Пятеро из них больны ветрянкой. Определить вероятность того, что два наугад вызванных пациента не больны ветрянкой? (Ответ: 0,43)
Студент знает 20 из 25 вопросов программы. Определить вероятность того, что студент не знает предложенные экзаменатором два вопроса. (Ответ: 0,03)
Для некоторой местности среднее число пасмурных дней в июле равно шести. Найти вероятность того, что первого и второго июля будет пасмурно.(Ответ: 0,032)
Найдите вероятность того, что в семьях с двумя детьми оба ребенка - мальчики. Вероятность рождения мальчика равна 0,515. (Ответ: 0,265)
ТЕМА: Формула полной вероятности
Задачи
На приеме у врача 10 пациентов, четверо из которых больны гриппом. Вероятность повышения температуры в группе с гриппом равна 0,8, а в другой группе - 0,6. Определить вероятность того, что у наугад выбранного пациента повышена температура. (Ответ: 0,68)
На участке у врача 40 человек, у которых с вероятностью 0,3 встречается инфекционно-аллергический полиартрит. На другом участке 60 человек, и данное заболевание встречается с вероятностью 0,5. Определить вероятность того, что наугад выбранный пациент болен инфекционно-аллергическим полиартритом. (Ответ: 0,42)
На участке у врача находятся 2 группы больных. В 1-й группе 6 человек, у которых с вероятностью 0,3 встречается инфекционно-аллергический полиартрит. 2-я группа состоит из 10 человек, и данное заболевание встречается с вероятностью 0,5. Определить вероятность того, что наугад выбранный пациент болен инфекционно-аллергическим полиартритом. (Ответ: 0,425)
В поликлинике принимают два врача стоматолога. Вероятность попасть на прием к первому врачу - 0,4, ко второму - 0,6. Вероятность повторного обращения к стоматологу для первого врача равна 0,2; для второго - 0,15. Определите вероятность того, что наугад выбранному пациенту придется обращаться к врачу повторно. (Ответ: 0,17)
Вероятность того, что при работе ЭВМ возникнет сбой в АЛУ - 0,4; в ОЗУ - 0,6. Вероятность обнаружения сбоя в АЛУ - 0,9; в ОЗУ - 0,85. Определить вероятность того, что возникший в машине сбой будет обнаружен. (Ответ: 0,87)
Студент может заболеть гриппом только в результате либо переохлаждения, либо контакта с другим больным. Вероятность переохлаждения равна 0,2, вероятность контакта с другим больным- 0,8. Вероятность заболеть гриппом при переохлаждении составляет 0,3, а при контакте - 0,1. Определить вероятность того, что наугад выбранный студент заболеет гриппом. (Ответ: 0,14)
На приеме у врача находится 10 пациентов, 3 из которых страдает гипертонической болезнью. Вероятность головной боли при гипертонии - 0,99, а в других случаях - 0,65. Определить вероятность того, что у наугад выбранного пациента головная боль. (Ответ: 0,752)
На приеме у врача 10 пациентов, четверо из которых больны гриппом. Вероятность повышения температуры в группе с гриппом - 0.81, во второй - 0,6. Определить вероятность того, что у наугад выбранного пациента повышена температура. (Ответ: 0,684)
В поликлинике принимают два врача стоматолога. Вероятность попасть на прием к первому врачу - 0,3, ко второму - 0,7. Вероятность повторного обращения к стоматологу для первого врача - 0,15, для второго - 0,1. Определите вероятность повторного обращения к стоматологу, если врач был выбран наугад. (Ответ: 0,115)
ТЕМА: Случайные величины и законы их распределенияТеоретическое вопросы
Дайте определение случайной непрерывной величины.
* Случайная величина, которая может принимать любые значения внутри некоторого интервала
Приведите примеры величин, которые можно отнести к случайным непрерывным величинам.
* Температура тела человека, артериальное давление, масса тела
Дайте определение случайной дискретной величины.
* Дискретной называется случайная величина, принимающая конечное или бесконечное счетное множество значений
Приведите примеры величин, которые можно отнести к случайным дискретным величинам.
* Число больных на приеме у врача, частота пульса
Перечислите основные характеристики случайных величин.
* Математическое ожидание, дисперсия, моменты
По какой формуле вычисляется математическое ожидание для случайной дискретной величины?
* 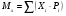
Какая формула используется для расчета дисперсии случайной дискретной величины?
* 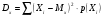
Какая формула используется для расчета среднего квадратического отклонения случайной дискретной величины?
* Ϭ= 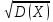
Какую размерность имеет значение дисперсии случайной величины?
* Размерность квадрата случайной величины.
Какую размерность имеет значение математического ожидания случайной величины?
* Размерность случайной величины
Какую размерность имеет значение среднего квадратического отклонения случайной величины?
* Размерность квадратного корня случайной величины
Почему при описании случайной величины чаще пользуются средним квадратическим отклонением, чем дисперсией?
* Для приведения в соответствие размерности разброса случайной величины с размерностью самой случайной величины
Случайную величину X увеличили в "а" раз. Как при этом изменится математическое ожидание этой случайной величины?
* Увеличится в "а" раз
Случайную величину X уменьшили в "а" раз. Как при этом изменится дисперсия этой случайной величины?
* Уменьшится в "а 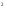 " раз ТЕМА: Случайные величины и законы их распределенияЗадачи
Найти математическое ожидание случайной величины, образующейся при бросании правильного однородного тетраэдра с пронумерованными гранями 1,2,3,4. (Ответ: 2,5)
Найти математическое ожидание случайной величины, образующейся при бросании правильного однородного додекаэдра с пронумерованными гранями 1,2,3,4,5,6,7,8,9,10,11,12. (Ответ: 6,5)
Найти среднеквадратичное отклонение случайной величины, если ее дисперсия принимает значение, равное 4. (Ответ: 2)
Найти среднее квадратическое отклонение случайной величины, если ее дисперсия принимает значение, равное 100. (Ответ: 10)
При изучении электрического сопротивления кожи до введения атропина установлен приведенный ниже закон распределения случайной величины. Найдите математическое ожидание случайной величины. (Ответ: 9.)
X
|
5
|
7
|
8
|
10
|
12
|
ш
|
10
|
30
|
10
|
20
|
30
|
При изучении электрического сопротивления кожи после введения атропина установлен приведенный ниже закон распределения случайной величины. Найдите математическое ожидание случайной величины. (Ответ: 8,35)
X
|
6
|
7,2
|
8,9
|
9,3
|
10,2
|
р
|
0,1
|
0,3
|
0,2
|
0,3
|
0,1
|
При изучении электрического сопротивления кожи до введения атропина установлен приведенный ниже закон распределения случайной величины. Найдите дисперсию случайной величины, если ее математическое ожидание принимает значение 9. (Ответ: 5,8)
X
|
5
|
7
|
8
|
10
|
12
|
m
|
1
|
3
|
1
|
2
|
3
|
При изучении электрического сопротивления кожи после введения атропина установлен приведенный ниже закон распределения случайной величины. Найдите дисперсию случайной величины, если ее математическое ожидание принимает значение 8. (Ответ: 1,4)
X
|
6
|
7
|
8
|
9
|
10
|
Р
|
0,1
|
0,3
|
0,2
|
0,3
|
0,1
|
ТЕМА: Математическая статистикаТеоретические вопросы
В каких случаях требуется знание коэффициента Стьюдента?
* Для расчета доверительного интервала
Что называют доверительным интервалом?
* Интервал, в котором с заданной доверительной вероятностью находится среднее значение генеральной совокупности
Когда пользуются интервальной оценкой случайной величины?
* Для оценки среднего значения генеральной совокупности по малой выборке
Что называют генеральной совокупностью?
* Большая статистическая совокупность, из которой отбирается часть объектов для исследования
Что называют выборочной совокупностью?
* Часть объектов генеральной совокупности, выбранных случайным образом, как объект исследования
Что называют статистическим распределением?
* Совокупность вариант и соответствующих им частот
Что называют полигоном частот?
* Ломаная линия, соединяющая точки с координатами (Xi,Pi) ТЕМА: Сравнение 2-х статистических совокупностейТеоретические вопросы
В каких случаях применяется критерий Стьюдента?
* Для выявления достоверности различия между двумя статистическими совокупностями
По какой формуле рассчитывается фактическое значение критерия Стьюдента?
*
В каких случаях используется критерий Фишера?
* Это критерий рассеяния, применяемый для проверки равенства дисперсий из двух выборок
По какой формуле рассчитывается фактическое значение критерия Фишера?
В каких случаях используется критерий знаков?
* Критерий знаков используется при проверке нулевой гипотезы о равенстве медиан двух непрерывно распределенных случайных величин
Какие вы знаете параметрические критерии оценки для сравнения двух статистических совокупностей?
* Критерий Фишера и критерий Стьюдента
Какие вы знаете непараметрические критерии оценки для сравнения двух статистических совокупностей?
*
Можно ли использовать критерий Фишера для сравнения двух статистических совокупностей, которые не подчиняются закону Гаусса?
Можно ли использовать критерий Стьюдента для сравнения двух статистических совокупностей, которые не подчиняются закону Г аусса?
Можно ли использовать критерий знаков для сравнения двух статистических совокупностей, которые не подчиняются закону Г аусса?
ТЕМА: Сравнение 2-х статистических совокупностей
Задачи
При исследовании влияния радиации на всхожесть семян экспериментатор установил, что данные, полученные в эксперименте, не подчиняются нормальному закону распределения. Какой критерий можно использовать в данном случае, чтобы выявить влияние радиации на всхожесть семян? (Ответ: критерий знаков)
При изучении влияния некоторого препарата на стабилизацию уровня сахара в крови было установлено, что средние значения сахара до введения препарата и после введения одинаковые. Какой критерий можно использовать в данном случае, чтобы выявить влияние препарата?
(Ответ: критерий Фишера)
При исследовании влияния нагрузки на уровень холестерина в крови оказалось, что среднее значение холестерина до нагрузки и после разное. Полученные данные подчиняются нормальному закону распределения. Какой критерий можно использовать в данном случае, чтобы сделать вывод о влиянии нагрузки на содержание холестерина в крови? (Ответ: критерий Стьюдента)
Сравнивая 2 статистические совокупности, экспериментатор получил значение критерия Фишера Рф=4,56. Табличное значение для данных объемов выборок равно 6,7. Какой вывод должен сделать экспериментатор из полученных данных? (Ответ: верна нулевая гипотеза)
Сравнивая 2 статистические совокупности, экспериментатор получил значение критерия Стьюдента 1Ф=3,17. Табличное значение для данных объемов выборок равно 2,9. Какой вывод должен сделать экспериментатор из полученных данных? (Ответ: полученная в опыте разница между исходными данными статистически достоверна)
Сравнивая 2 статистические совокупности, экспериментатор получил значение критерия знаков Z,},=14. Табличное значение для данных объемов выборок равно 19. Какой вывод должен
сделать экспериментатор из полученных данных. (Ответ: верна нулевая гипотеза)
Сравнивая 2 статистические совокупности, экспериментатор получил значение критерия Фишера Рф=б,56. Какой вывод должен сделать экспериментатор. (Ответ: для вывода
недостаточно данных)
ТЕМА: Коэффициент корреляции и его свойства.
Уравнения регрессии
Теоретические вопросы
В каком интервале находятся значения коэффициента корреляции?
* От 0 до 1
Какие значения коэффициента корреляции указывают на слабую тесноту связи между исследуемыми величинами?
*-0.125 , 0.18
Какие значения коэффициента корреляции указывают на среднюю тесноту связи между исследуемыми величинами?
* -0.625 , 0.48
Какие значения коэффициента корреляции указывают на сильную тесноту связи между исследуемыми величинами?
* 0.95 , -0.84 , 0.72
Какую информацию можно получить, построив корреляционное поле?
* По виду корреляционного поля можно сделать вывод о наличии или отсутствии связи между исследуемыми величинами и определить тип этой связи
Экспериментатор сделал расчет коэффициента корреляции и получил значение г=0,15. Какой вывод можно сделать?
*
Экспериментатор сделал расчет коэффициента корреляции и получил значение г=-0,62. Какой вывод можно сделать?
* Связь между исследуемыми величинами обратная и средняя
Экспериментатор сделал расчет коэффициента корреляции и получил значение г=1,7. Какой вывод можно сделать?
* Экспериментатор ошибся в расчетах
Какую связь отражает уравнение регрессии?
* Зависимость среднего значения одной величины от конкретного значения другой величины
При каких значениях коэффициента корреляции целесообразно строить теоретическую линию регрессии?
* От 0.1 до 0.8
ТЕМА: Элементы теории информации
Теоретические вопросы
Что называется информационной энтропией?
* Мера неопределенности в системе
Чему равна энтропия системы, которая может находится в n равновероятных состояниях?
* 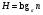
По какой формуле рассчитывается энтропия системы, которая может находиться в n неравновероятных состояниях?
* 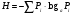
Дайте наиболее полное определение информации.
* Информация - это совокупность сведений, сообщений о явлениях, процессах, предметах, привносящие новые знания об этих явлениях, процессах, предметах
Дайте определение единицы информации 1 бит.
* Бит - это количество информации, заключенное в сообщении о том, что произошло одно из двух равновероятных событий
Что называется пропускной способностью канала связи?
* Максимальное количество информации, которое можно передать по каналу связи в единицу времени
В каком случае информационная энтропия системы принимает минимальное значение
* Если система может находиться только в одном состоянии
В каком случае информационная энтропия системы принимает максимальное значение?
* Если все состояния системы равновероятны
ТЕМА: Элементы теории информации.
Задачи.
Грани правильного тетраэдра пронумерованы. Определите количество информации, заключенное в сообщении о том, что тетраэдр выпал гранью 4? (Ответ: 2 бита)
Определите количество информации, заключенное в сообщении о том, что из колоды карт выпала карта валет пиковый? Вся колода состоит из 32 карт. (Ответ: 5 бит)
Определите количество информации, заключенное в сообщении состоящем из 4 символов, если весь алфавит сообщений содержит 8 символов. (Ответ: 12 бит)
Какое количество информации содержится в сообщении о том, что данный нуклеотид в молекуле ДНК содержит цитозин, если известно, что в ДНК с одинаковой частотой встречаются азотистые основания четырех типов. (Ответ: 2 бита)
Определите энтропию системы, которая может находиться в трех состояниях с вероятностями: 0,25, 0,25, 0,5 соответственно.(Ответ: 1,5 бита)
Определите энтропию двумерной характеристики данного вида растения, которое может иметь один из 8 видов цветов и одну из 4 форм листа. (Ответ: 5 бит)
Определите количество информации, которое получит экспериментатор при однократном изъятии шарика из урны, если в урне находится 15 черных, 15 красных, 15 зеленых и 15 белых шаров. (Ответ: 2 бита)
Определите количество информации, которое получит экспериментатор-дальтоник, воспринимающий красный и зеленый цвет как один при однократном изъятии шарика из урны. В урне находится 25 черных, 25 красных, 25 зеленых и 25 белых шаров. (Ответ: 1,5 бита)
Определите пропускную способность канала связи, если при передаче информации в течение 24 секунд было передано 2640 бит информации. (Ответ: 110 бит/с)
Определите количество информации, заключенное в сообщении о событии, вероятность наступления которого равна 0,5 .(Ответ: 1 бит)
Определите энтропию системы, которая может находиться в 8 равновероятных состояниях. (Ответ: 3 бита)
Определите энтропию системы: колода карг (32 карты) и тетраэдр. (Ответ: 7 бит)
Определите пропускную способность канала связи, если при передаче информации в течение 16 секунд было передано 192 бита информации. (Ответ: 12 бит/с)
Какое количество информации было передано по каналу связи в течение 15 секунд, если пропускная способность его 20 бит/с? (Ответ: 300 бит)
Как долго осуществлялась передача информации, если при пропускной способности канала связи 25 бит/с было передано 600 бит информации? (Ответ: 24 с)
ТЕМА: Сенсорные системы
Теоретические вопросы
Как формулируется закон Вебера?
* Отношение минимально определяемого изменения силы стимула к величине этого стимула есть величина постоянная
Как в аналитическом виде выглядит закон Вебера?
*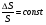
Как в аналитическом виде выглядит закон Стивенса.
* 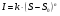
Как в аналитическом виде выглядит закон Вебера-Фехнера.
*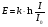
Дайте определение абсолютного порога ощущения.
* Минимальное значение силы стимула, вызывающее появление ощущения
Дайте определение максимального абсолютного порога ощущения?
* Максимальное значение интенсивности ощущений при действии внешних стимулов
Дайте определение дифференциального пространственного порога?
* Наименьшее расстояние между раздражителями, при котором последние воспринимаются как раздельные
Дайте определение дифференциального временного порога?
* Минимальное время действия стимула, которое мы способны дифференцировать в своих ощущениях
Дайте определение психофизического направления?
* Направление, устанавливающее связь между характеристиками различных свойств вызвавших их раздражений
ТЕМА: Физическая оптика
Что называется оптическим путем?
* Произведение геометрического пути на показатель преломления среды
Что называется интерференцией света?
* Перераспределение интенсивности света в результате наложения (суперпозиции) нескольких световых волн
Что называется дифракцией волн?
* Явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн
Что называется поляризацией света?
* Процесс упорядочения колебаний вектора напряжённости электрического поля световой волны при прохождении света сквозь некоторые вещества (при преломлении) или при отражении светового потока
Выберите условие максимума интенсивности света при интерференции.
*
Выберите условие минимума интенсивности света при интерференции.
*
Выберите формулировку принципа Гюйгенса?
* Образующиеся вторичные волны являются когерентными и интерферируют между собой
Выберите формулировку принципа Френеля?
* Каждая точка волн. пов.,кот достиг волна явл ист вторичных сферических волн
Выберите формулу для дифракционной решетки.
* 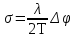
Что называется поляризатором?
* Устройство, предназначенное для получения полностью или частично поляризованного оптического излучения из излучения с произвольным состоянием поляризации
Выберите формулу для закона Малюса.
* 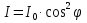
Выберите формулу для определения утла поворота плоскости поляризации плоскополяризованного света.
*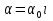
Выберите формулу закона Брюстера.
*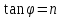
Какие вещества называют оптически активными?
* Это способность среды (кристаллов, растворов, паров вещества) вызывать вращение плоскости поляризации проходящего через неё оптического излучения (света)
Оптическая разность хода двух когерентных лучей составляет
мкм. Определить результат интерференции лучей с длиной волны 640 нм. (Ответ: максимум)
Оптическая разность хода двух лучей, полученных от независимых источников, составляет 6,4 мкм. Определить результат интерференции лучей с длиной волны 640 нм. (Ответ: интерференция отсутствует)
Оптическая разность хода двух когерентных лучей составляет
мкм. Определить результат интерференции лучей с длиной волны 640 нм. (Ответ: минимум)
Разность хода двух интерферирующих волн в вакууме равна 0. Чему равна соответствующая разность фаз? (Ответ: 0)
Разность хода двух интерферирующих волн в вакууме равна 0,2 длины волны. Чему равна соответствующая разность фаз? (Ответ: 72°)
Разность фаз двух интерферирующих волн в вакууме равна те/3. Скольким длинам волн в вакууме будет соответствовать оптическая разность хода этих волн? (Ответ: А/6)
На пути луча света перпендикулярно ему поставлена стеклянная пластинка (п = 1,5) толщиной 1=1 мм. На какую величину изменится оптическая длина пути? (Ответ: 0,5 мм)
Определите толщину кварцевой пластинки для которой угол поворота плоскости поляризации света с длиной волны 500 нм равен 48°. Постоянная вращения кварца для этой длины волны 30 град./мм. (Ответ: 1,6 мм)
Раствор сахара, налитый в трубку длиной 1=20 см и помещенный между поляризатором и анализатором, поворачивает плоскость поляризации света (А=0,5 мкм) на а=30°. Найдите (в г/см3) концентрацию сахара в растворе, если удельное вращение сахара для этой длины волны [а0]=6,67 град см2/г. (Ответ: 0,22 г/см3)
При прохождении света через слой толщиной lj = 10 см 10%-ного раствора сахара плоскость поляризации света повернулась на угол aj =17°. В растворе сахара с неизвестной концентрацией сахара, при прохождении света через слой толщиной І2 = 25 см, плоскость поляризации повернулась на угол 0.2 =34°. Найдите концентрацию второго раствора. (Ответ: 8%).
Между николями, расположенными под 45°, поместили пластинку кварца толщиной / =1,5 мм, в результате чего поле зрения стало максимально светлым. Определите постоянную вращения используемого в опыте кварца для монохроматического света. (Ответ: 30 град/мм)
Угол падения светового луча на некоторое вещество равен 60°. Определите показатель преломления вещества, если отраженный от вещества луч полностью поляризован? (Ответ:
1,7)
Два николя расположены так, что угол между их главными плоскостями составляет 60°. Как изменится интенсивность естественного света при прохождении его через первый НИКОЛЬ? (Ответ: уменьшится в 2 раза)
ТЕМА: Геометрическая оптика
Теоретические вопросы
ЗАДАНИЕ № 1
Какие из перечисленных недостатков относятся к оптической системе глаза?
* Астигматизм, обусловленный недостатком оптической системы, дальнозоркость, близорукость
ЗАДАНИЕ № 2
Какие из перечисленных погрешностей относятся к оптическим системам?
* Астигматизм, обусловленный асимметрией оптической системы, сферическая аберрация, астигматизм косых пучков, дисторсия, хроматическая абеpрация
ЗАДАНИЕ № 3
В чем заключается сферическая аберрация?
* Периферические части линзы сильнее отклоняют лучи, идущие от источника S на оси, чем центральные.
ЗАДАНИЕ № 4
В чем заключается хроматическая аберрация?
* Пучок белого света, идущий параллельно главной оптической оси, будет фокусироваться в разных точках, разлагаясь в спектр.
ЗАДАНИЕ № 5
В чем заключается дисторсия?
* Лучи, посылаемые предметом в систему, составляют большие углы с оптической осью, при этом зависимость линейного увеличения от угла пучка приводит к нарушению подобия изображения и предмета.
ЗАДАНИЕ № 6
В чем заключается астигматизм?
* Сферическая световая волна, проходя через оптическую систему, деформируется и перестает быть сферической.
ЗАДАНИЕ № 7
Что называется фокусным расстоянием центрированной оптической системы?
* Расстояние между фокусами и соответствующими главными точками.
ЗАДАНИЕ № 8
Чему равно расстояние наилучшего зрения у взрослого человека?
* 25 см
ЗАДАНИЕ № 9
Что в медицине принимают за норму остроты зрения?
* 1
ЗАДАНИЕ № 10
Выберите формулу для расчета увеличения окуляра микроскопа.
* 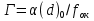
ЗАДАНИЕ № 11
Выберите формулу для расчета увеличения объектива микроскопа.
* 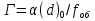
ЗАДАНИЕ № 12
Выберите формулу для расчета увеличения микроскопа.
*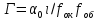
Геометрическая оптика
Задачи
ЗАДАНИЕ № 1
Какое увеличение дает лупа, если расстояние наилучшего зрения 27 см.
Фокусное расстояние 3 см?
* 9
ЗАДАНИЕ № 2
Определите расстояние наилучшего зрения, если получено четкое десятикратное увеличение предмета при помощи лупы, имеющей фокусное расстояние 3 см.
* 30
ЗАДАНИЕ № 3
Определите увеличение окуляра микроскопа, если фокусное расстояние окуляра F = 5см.
* 5
ЗАДАНИЕ № 4
Определите увеличение объектива микроскопа, если длина тубуса микроскопа 1,2 м , фокусное расстояние объектива 10 см.
*
ЗАДАНИЕ № 5
Рассчитайте увеличение микроскопа, если Fok=3 cm, Fo6=l,5 см ,L=20см
* |
|
|
 Скачать 89.92 Kb.
Скачать 89.92 Kb.
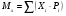
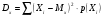
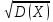
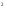 " раз
" раз