Элементы вариационного исчисления
 Скачать 57 Kb.
|
|
Элементы вариационного исчисления. При решении инженерных задач, которые описываются с помощью мат. модели,состоящая из дифференциального уравнения и краевых условий, т.е.   (1){  (2)Наряду с аналитическими и численными методами используются элементы вариационного исчисления. А именно мат. модели (1) – (2) ставится в соответствии некий функционал, минимум которого может быть решением краевой задачи (1) – (2). Поэтому ниже рассмотрим некоторые основные понятия элементов вариационного исчисления. Первой задачей вариационного исчисления была задача о брахистохроне, сформулированный Бернулли в 1696 г. в этой задаче необходимо было найти кривую у(х), таким образом, чтобы минимизировать время спуска по этой кривой из одной точки в другую. Бернулли показал, что время спуска записывается в виде: 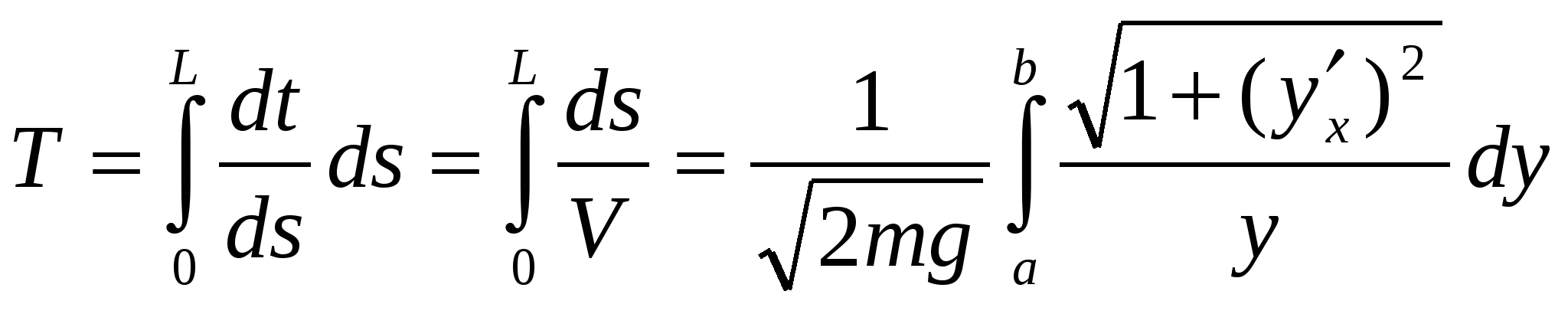 (3)Выражение 3 показывает, что Т=Т[e], т.е. может быть функцией от у, и называется функционалом, т.е. его переменная является функцией. В общем виде выражении 3 записывают так:  (4)Итак сформулируем главную цель вариационного исчисления. Найти функцию у. которая доставляла бы max(min) функционала (4), в соответствии с этим стратегия поиска экстремума функционала (4) будет такой же как и нахождение экстремума функций в мат. анализе, т.е. сначала находим критические точки из условия у'(х)=0 и далее определяем max или min. В вариационном же исчислении подход остаётся прежним, но аргументом здесь может быть не числовая переменная, а функции. В вариационном исчислении мы вычисляем так называемую функциональную производную, т.е. производную по функции у=у(х) и далее приравниваем её к нулю и место критических точек из курса мат. анализа мы получаем обыкновенное дифференциальное уравнение (ОДУ) известное как уравнение Эйлера-Лагранжа решая которое, при соответствующих краевых условиях мы получаем функцию (решение) которое даёт минимум исходному функционалу вариационного исчисления, таким образом задача нахождения минимума функционала сводится к нахождению решения краевой задачи для ОДУ. Минимизация функционала 4 Рассмотрим минимизацию функционала на классе гладкой функции, удовлетворяющих условию у(а)=А у(в)=В (5) Далее рассмотрим вариацию гладкой функции у(х) равной  , где  А функция …  удовлетворяет краевым условиям: (6)Ясно, что функционал  при всех   .Здесь функционал  ведёт себя как функция  следующим образом: Если мы возьмём производную  по параметру и приравняем к нулю то получим выражение  Далее интегрируя этот интеграл по частям получаем:  Поскольку последний интеграл обращается при любой функции n(x) получаем  (7)Уравнение(7) называется уравнением Эйлера-Лагранжа Замечание. Хотя уравнение (7) кажется сложным, но после подставления конкретной функции оно выглядит менее сложным и превращается в обыкновенное дифференциальное уравнение 2-го порядка относительно у(х), решая уравнение(7). Мы находим функцию у(х). которая даёт min исходному функционалу, на класс гладких функций. Замечание 1 Основную роль играет уравнение Эйлера-Лагранжа, т.к. после подставления явного вида функции F в него получаем то или иное ДУ 2-го порядка решение которое находится обыкновенными методами. Замечание 2 В методе вариационного исчисления основной задачей является запись функционала I(y) затем из уравнения Эйлера-Лагранжа получим ОДУ 2-го порядка и его решение. |