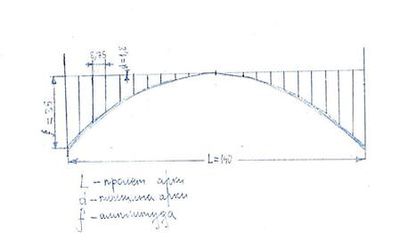
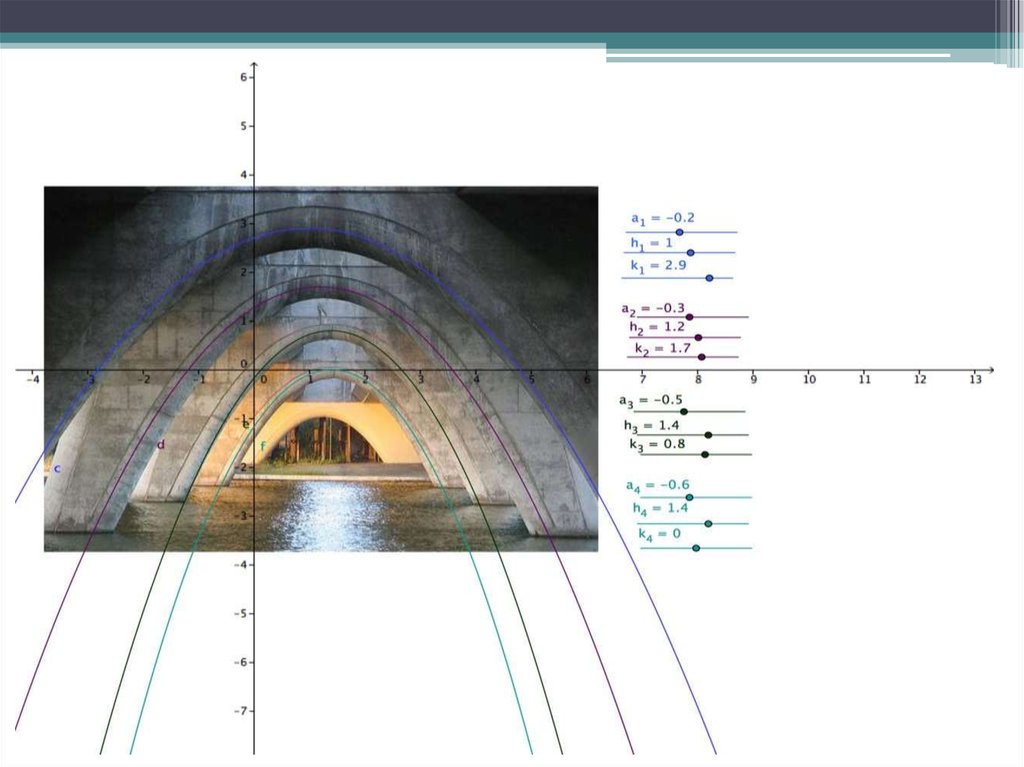
Проектная работа Параболы в арочных мостах. Параболы в арочных мостах. Енисейская православная гимназия
 Скачать 2.93 Mb. Скачать 2.93 Mb.
|
|
МОСКОВСКИЙ ПАТРИАРХАТ ЕНИСЕЙСКАЯ ЕПАРХИЯ ЧАСТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ “ЕНИСЕЙСКАЯ ПРАВОСЛАВНАЯ ГИМНАЗИЯ” тел./факс (39 195) 2-50-63, 2-20-13 663180 ул. Кирова, 97, г.Енисейск, Красноярский край Сайт: http://www.eppg.clan.su E-mail: eppg@mail.ru ИНН 2447002241; КПП 244701001; ОКПО 21903338; ОГРН 1022401274532 ПРОЕКТНАЯ РАБОТА Тема проекта "Параболы в арочных мостах" Гимназист 9 класса Грудинина Светлана Петровна руководитель проекта Енисейск 2021 ОЦЕНОЧНЫЙ ЛИСТ ПРОЕКТА 9 класс
ОглавлениеВведение 1. Что такое парабола? 2. Парабола – график квадратичной функции, её свойства и график. Парабола в мостостроении. 3. Из истории мостостроения в России с XII по XIX века. 4. Виды мостов. 5. Арочные мосты. Заключение Используемая литература Введение Ни одного архитектурного сооружения в нашем мире не существовало бы без предварительных точных расчетов, которые помогает делать наука под названием математика. В повседневной жизни довольно часто нам встречаются дугообразные конструкции; эта форма широко распространена не только из-за эстетичного внешнего вида, но и из-за способности выдерживать нагрузки, вызываемые весом самого сооружения и дополнительными факторами (сейсмическая активность в регионе, транспорт и т.д.). К таким сооружениям относятся арки, купола храмов, акведуки, однако в этой работе будут рассмотрены мосты. В процессе работы над индивидуальным исследовательским проектом по математике на тему "Параболы в арочных мостах" была поставлена цель, изучить материал о свойствах квадратичной функции и ее графика - параболы, исследовать графики квадратичной функции в арочных мостах. Работа интересна, так как рассматривается теоретическая база о построении арочных мостов с применением принципа параболы. Создан буклет красивейших арочных мостов с применением принципа параболы. В исследовательском проекте по математике представлена теория квадратичной функции и ее графика, найдены арочные мосты и представлены их фотографии с выделением параболы. Цель работы: Изучить материал о свойствах квадратичной функции и ее графика- параболы и исследовать графики квадратичной функции в арочных мостах. Для достижения цели я поставил следующие задачи: Изучить литературу про мосты. Изучить теорию квадратичной функции и ее графика. Найти арочные мосты. Объект исследования: Арочные мосты. Предмет исследования: свойства параболы, применяемые при строительстве арочных мостов. Продукт научно-исследовательской работы: презентация, буклет с красивейшими арочными мостами с применением принципа параболы. Что такое парабола. Пара́бола (греч. παραβ ολή — приложение) —кривая , точки которой одинаково удалены от некоторой точки, называемой фокусом, и от некоторой прямой, называемой директрисой параболы. Наряду с эллипсом и гиперболой, парабола является коническим сечением. Изображение конического сечения, являющегося параболой. Построение параболы как конического сечения. 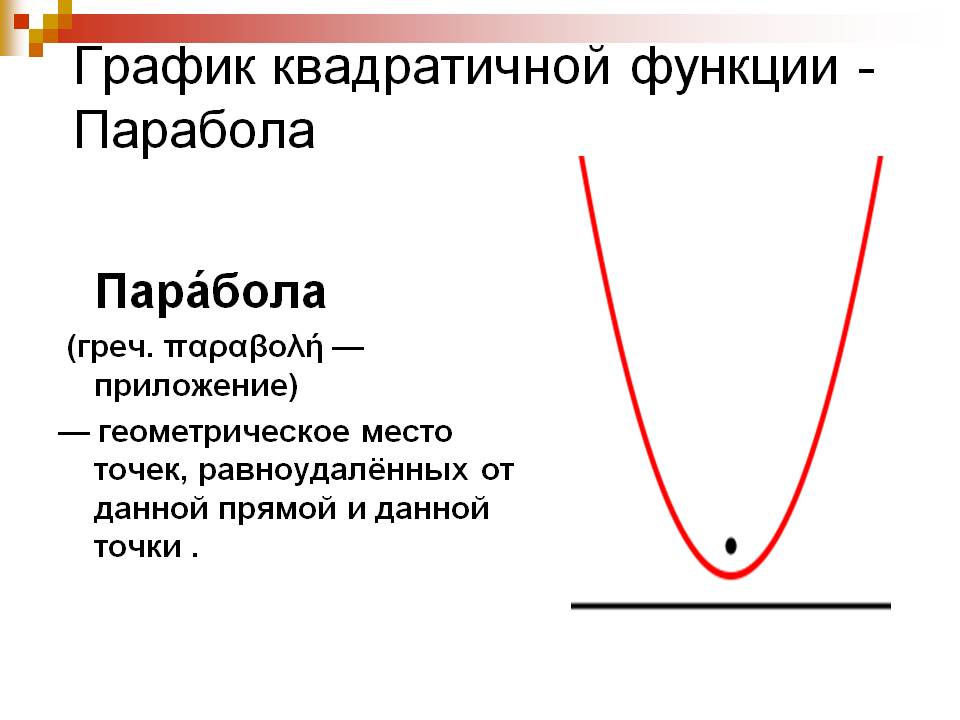 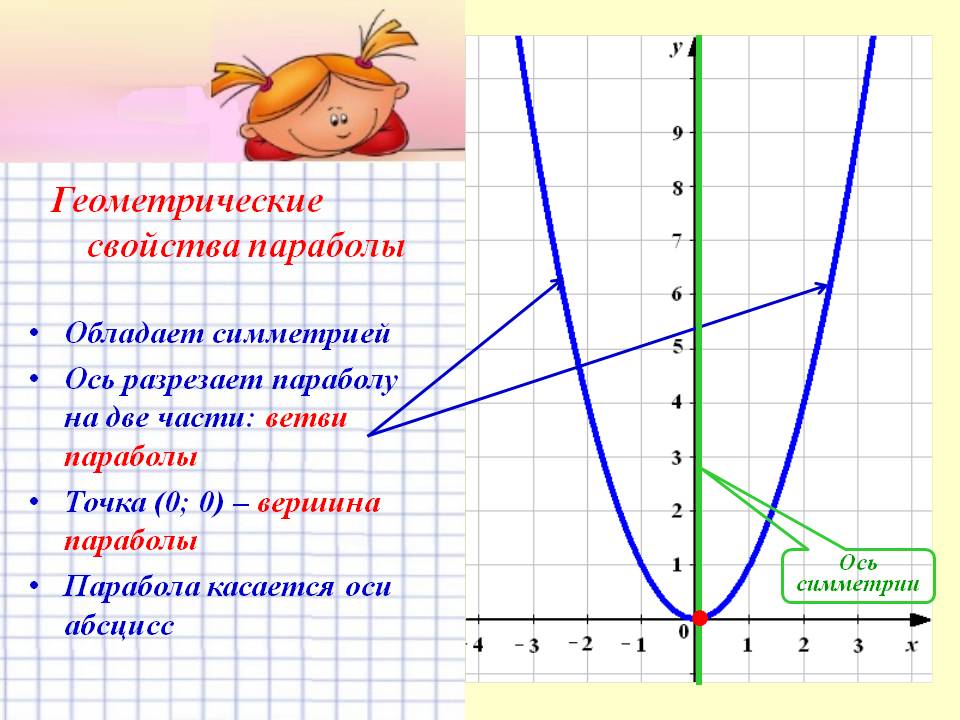 Парабола — кривая второго порядка. Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе. Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей. Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе. Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб. При вращении параболы вокруг оси симметрии получается эллиптический параболоид. 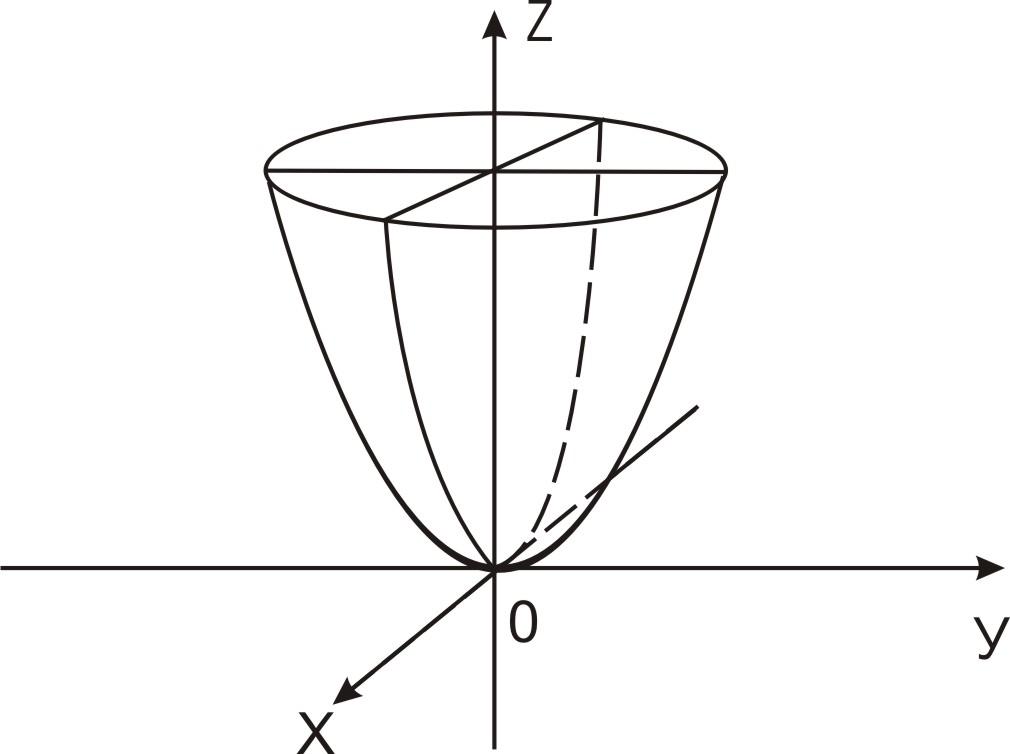 2. Парабола – график квадратичной функции, её свойства и график. Функция вида y=ax^2+bx+c, где a, называется квадратичной. Графиком этой функции является парабола. Парабола – это геометрическое место точек, равноудаленных от данной прямой и данной точки. 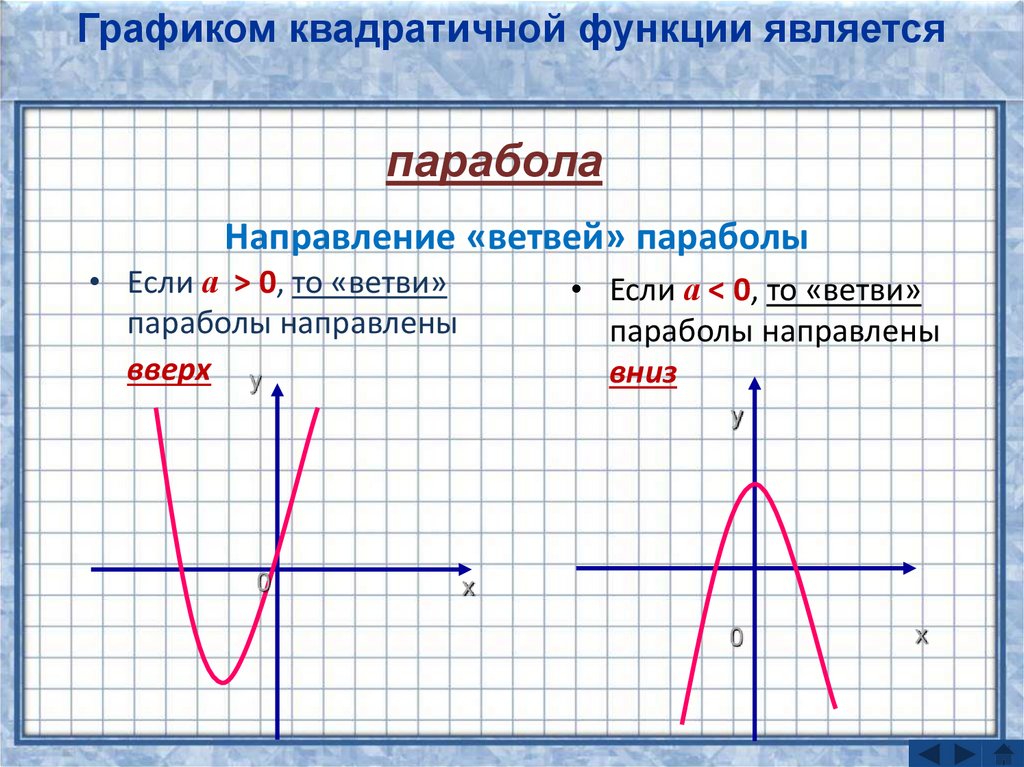 Чтобы построить график функции вида y=ax^2+bx+c, нужно найти координаты вершины графика. Х вершины = (-b)/2a; для нахождения у вершины нужно подставить значение найденного x в данное уравнение; график функции y=ax2+bx+c получается из графика функции у=aх2 сдвигом в точку (х вершины; у вершины). 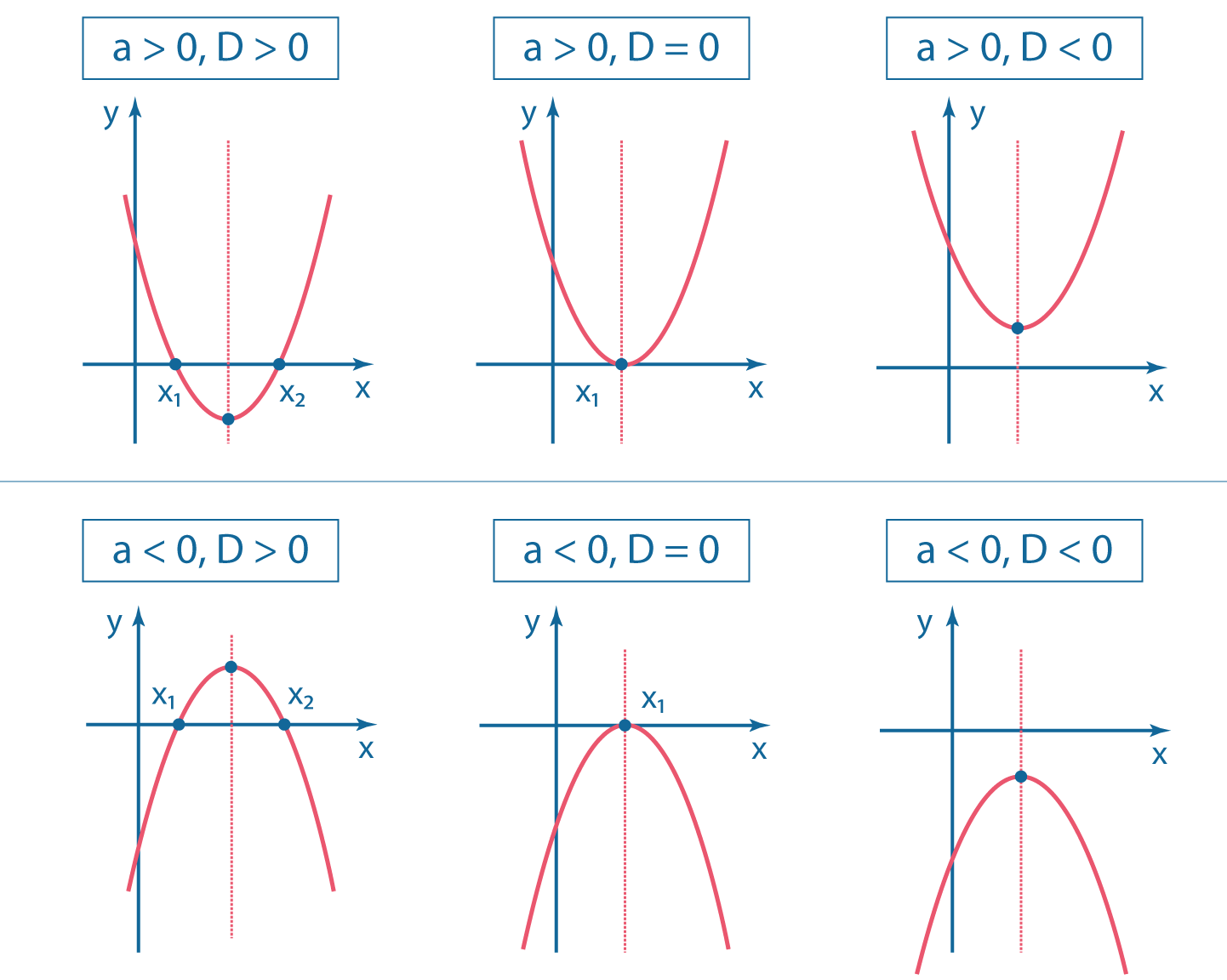 Довольно часто мы сталкиваемся с параболическими формами. Например, во время или после дождя мы наблюдаем радугу. В лепестках некоторых цветов, в очертании горных хребтов и вершин можно разглядеть параболу. Гуляя по городу, мы часто видим дугообразные конструкции. Архитекторы используют параболическую форму в проектировании арок, мостов, куполов, потолков. Во-первых, именно такая форма придает эстетичный вид, во-вторых, параболическим конструкциям присуща прочность, потому что сила, создаваемая нагрузкой на мост или арку, не толкает вниз, а распределяется вдоль дуги, то есть эти строения поддерживают сами себя. В куполах всех храмов и церквей используется этот же принцип. Прежде чем рассматривать виды мостов и их преимущества, познакомимся с историей мостостроения в России. 3.Из истории мостостроения в России с XII по XIX века.Постройка мостов, вероятно, началась очень давно. При Владимире Мономахе в 1115 году был построен наплавной мост через Днепр в Киев, при Дмитрии Донском во время осады Твери были построены 2 моста, а во время войны с татарами в 1380 году возвели мост через Дон. Кроме того, в Новгородской летописи упоминается о «разборчатых» мостах в Новгороде через реку Волхов.  Мост 12 века через реку Волхов Наплавные мосты состояли из закрепленных между собой плотов и лодок. Именно наплавные мосты были наиболее распространены в России в этот период из-за простоты и дешевизны конструкции. Возводной мост, прилегавший к городской стене, делался подъемным. Первое указание относительно употребления таких мостов относится к 1229 году. Механизм, приводивший мост в движение, состоял из коромысла, который вращался между столбами, и цепей. Первый каменный мост начали строить в 1643 году при Михаиле Федоровиче Романове, однако в связи со смертью царя в 1645 году строительство было остановлено. Только в 1687 году первый каменный мост был открыт. С воцарением Петра Великого инженерное искусство развивалось неимоверно быстро, но при царе мостов не строилось. Петр I воспринимал Петербург как крупнейший порт, куда прибывали суды всех стран Европы, а мосты мешали судоходству. Также в городе на Неве ежегодно случались наводнения и штормовые бури, которые могли повредить конструкции. Но все же Петр I сделал исключение, издав приказ о строении деревянного моста, соединявшего Березовый и Заячий острова, с целью транспортировки грузов к Петропавловской крепости. Чугунные арочные мосты впервые появились в 1806 году в Петербурге при Александре I, это были первые металлические мосты в России. Были построены Полицейский, Красный, Синий, Поцелуев, Мало-Семеновский мосты. Цепные мосты введены в Россию в 1822 году по предложению французских инженеров. Распространение таких мостов захватило период с 1824 по 1853 год. К цепным мостам относятся Пантелеймоновский, пешеходные через Екатерининский канал и Мойку, Египетский, проволочный Лиговский через Западный Бур в Брест, мост через Нарву в Ивангород, Киевский через Днепр и Островский через реку Великую. До 1873 года из подвижных мостов с постоянными опорами применялись только подъемные с горизонтальной осью вращения. Поворотные мосты появились в первые в 1850 году при строительстве Николаевского моста в Петербурге и цепного моста в Киеве в 1853 году. 4. Виды мостовЭто – БАЛОЧНЫЙ, АРОЧНЫЕ, ВИСЯЧИЕ и ВАНТОВЫЕ. Балочный мостСамый первый, древний, простой и распространенный тип мостов – БАЛОЧНЫЙ. Он состоит из пролетного строения, опорных частей, опоры и фундамента. Пролетное строение или пролет, это и есть та самая балка, которая дала название всей системе подобных мостов. Прямоугольный брус лежащий на 2-х и более опор. Балка всегда прямая, работает она на изгиб. Человек придумал 2 системы этих мостов – разрезная и неразрезная. Разрезная система – это три разрезные балки упирающиеся на две опоры. Неразрезная система, когда одна балка перекрывает несколько пролетов весь мост целиком. У этих систем есть плюсы и минусы. Но большой минус этих систем – расстояние между опорами нельзя сделать слишком большим. Балка будет прогибаться под собственным весом и может просто рухнуть. В этих мостах самая простая конструкция и дешевая. Поэтому их построено больше всего в мире. 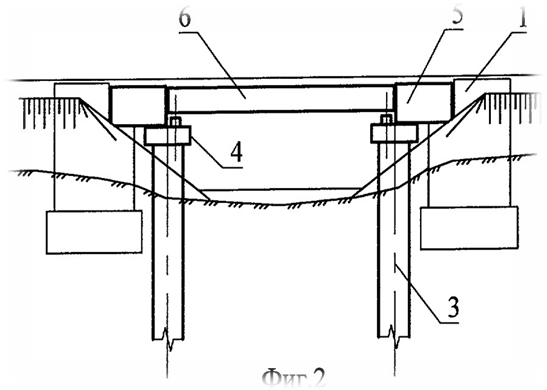  Висячий мост ВИСЯЧИЕ МОСТЫ – это ВЕНЕЦ ИНЖЕНЕРНОЙ МЫСЛИ. Все самые дорогие мосты и мосты с самой большой длиной пролета – это Висячие мосты. В них используют очень прочный материал. Несущая конструкция Висячего моста - гибкая нить. Она сможет быть в виде - троса, цепей, канатов, кабелей. Она работает только на растяжение, и в ней может быть использована высокопрочная сталь или современный материал - углеродное волокно. Нить крепится к фундаменту на земле, пропускается через пилоны, и уже к ней опять же с помощью канатов или тросов подвешивают проезжую часть. Висячие мосты одновременно очень гибкие и прочные позволяют перекрывать самые большие пролеты, поэтому их строят, как правило, через проливы и широкие реки . И все мировые рекорды длины за висячими мостами. Они позволили увеличить длину пролета по уму непостижимых размеров, но вместе с тем эти строения сложны и дороги. 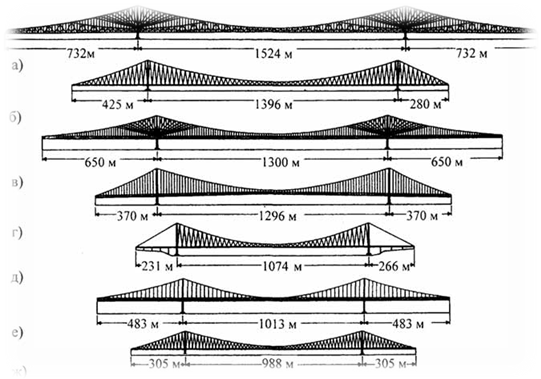  Вантовый мост Вантовые мосты часто называют разновидностью висячих. С тем же отличием, что стальные тросы от дорожного полотна идут непосредственно к пилонам, а не к гибкой нити наверху. Но на самом деле вантовые – это отдельный вид конструкции. ВАНТОВЫЕ МОСТЫ имеют прямолинейные ванты. Достоинством Вантовых мостов является возможность всей сборки в навес. Это значит, что постепенно от опоры в обе стороны наращивая пролетное строение, каждый раз поддерживая его своей опорой вант. В вантовых мостах балка жесткости поддерживается только прямолинейными вантами - тросами работающими на растяжение. Они сделаны из высокопрочной стали. 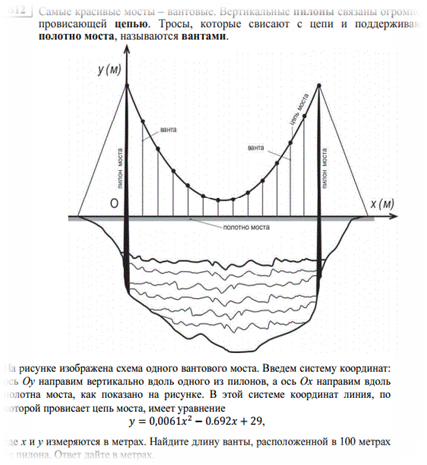  Арочные мосты. АРОЧНЫЕ МОСТЫ с анг. – ПРОСВЕРЛИВАМАЯ ДВЕРЬ. - это их природный аналог. Они отличаются тем, что представляют собой изогнутый брус, он как бы повторяет ту линию, которая возникает в балке при действии сгибающего момента. Арочный мост работает на сжатие, а не на изгиб, как балочный. Он держится, что называется за счет собственного веса. Поэтому такая конструкция построена из крепкого материала, не работающего на растяжение, из камня или бетона. Эти мосты самые прочные и меньше всего подвержены деформации. Они бывают небольшими пешеходными, а как правило все транспортные арочные мосты можно разделить: с проездом по низу; по середине; поверху. 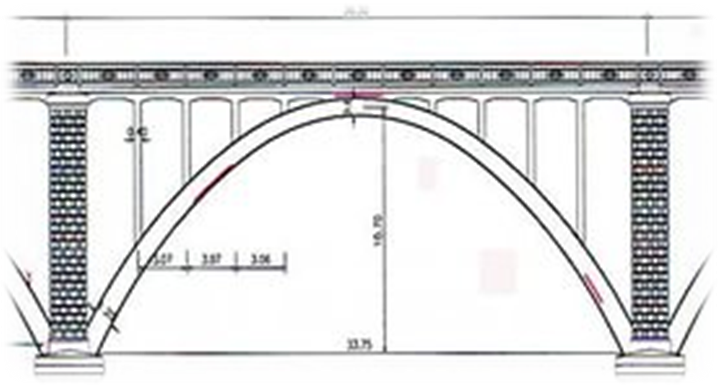 Чугунные арочные мосты Чугунные арочные мосты стали строить повсеместно. Пролеты мостов постепенно увеличивались. В России наиболее значительным чугунным арочным мостом являлся Николаевский мост в Петербурге (после революции был назван мостом Лейтенанта Шмидта). Он был построен в 1843-1850 гг. Мост имел пролеты по схеме: 32.1 + 36.9 + 42.9 + 46.8 + 42.9 +36.9 + 32.1 м. Полная длина моста составила 298 м. Проект майора-инженера С. В. Кербедза, архитектор А.П. Брюллов. В 1938 году пролетные строения моста заменены стальными сварными балками. |