Задачи для электриков в комплексных числах. задачи для электриков в компл числах. Это комплексное число

• Название: Это комплексное число
• Анкор: Задачи для электриков в комплексных числах
• Дата: 24.03.2023
• Размер: 157.74 Kb.
• Имя файла: задачи для электриков в компл числах.docx
• Тип: Документы; #1012541

. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2)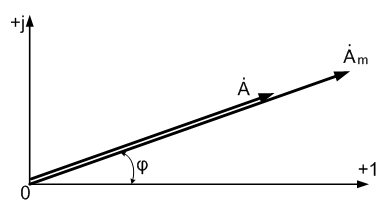



Рис.2. Комплексное число на комплексной плоскости

Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины. С учетом начальной фазы φ такое число записывают как  .

На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна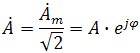



На рисунке выше этот вектор также показан.
Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли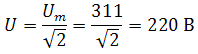



При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.
Итак, три формы записи комплексного числа:

1) показательная форма в виде



2) тригонометрическая форма в виде



3) алгебраическая форма



где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая.

Например, имеем комплексное число в показательной форме вида



в тригонометрической форме записи это запишется как



при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что





В итоге получим



где 

При переходе от алгебраической формы к показательной комплексное число вида



переходит к показательному виду  по следующим преобразованиям



а угол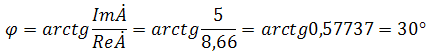



Таким образом, и получим



Перейдем к рассмотрению несложных примеров использования  символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода:

1. 
   
   
   1. 
      
      
      • 
        Составить комплексную схему, заменяя мгновенные значения ЭДС, напряжений и токов их комплексным видом
        
      • 
        В полученной схеме произвольно выбирают направления токов в ветвях и обозначают их на схеме.
        
      • 
        При необходимости составляют комплексные уравнения по выбранному методу решения.
        
      • 
        Решают уравнения относительно комплексного значения искомой величины.
        
      • 
        Если требуется, записывают мгновенные значения найденных комплексных величин.
        

Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.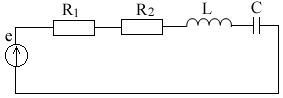



Рис.3. Схема с последовательным соединением элементов

Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.4):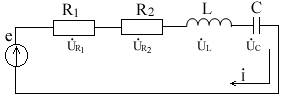



Рис.4. Схема с комплексными обозначениями

По закону Ома ток в цепи равен



где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как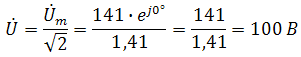



Пояснение: здесь начальная фаза φ = 0°, так как  общее выражение для мгновенного значения напряжение вида  приφ = 0° равно



Соответственно, комплекс входного напряжения в показательной форме запишется как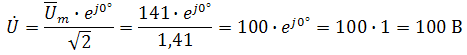



Полное комплексное сопротивление цепи в общем виде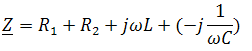



Находим комплексное сопротивление индуктивности



Находим комплексное сопротивление емкости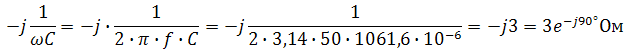



Соответственно, общее комплексное сопротивление цепи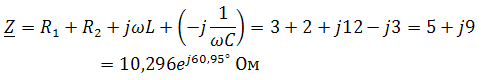



Ток в цепи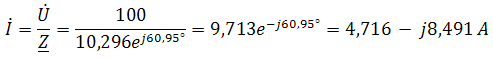



Комплексные напряжения на элементах

Комплексные напряжения на элементах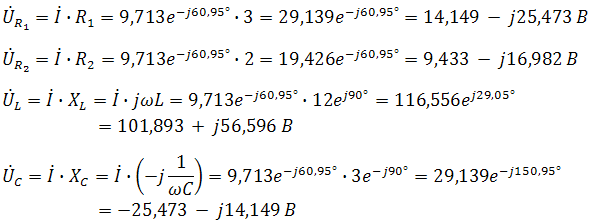



Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство 

Проверяем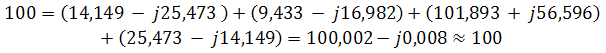



С небольшим расхождением из-за округлений промежуточных вычислений всё верно.

Пример 2.В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1)  полное сопротивление электрической цепи и его характер;
2)  действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;

1. 
   
   

Исходные данные: Е = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R3 = 10 Ом, С3 = 300 мкФ.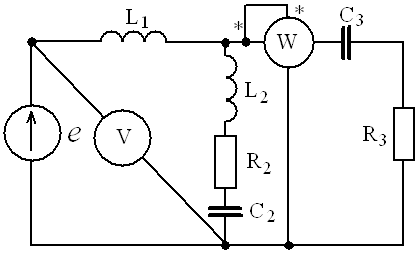



Рис.5.Цепь однофвзного синусоидального тока

Решение:
1.  Находим комплексные сопротивления ветвей и всей цепи:
Учитываем, что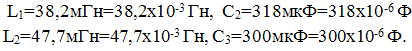



Комплексное сопротивление первой ветви:



Комплексное сопротивление второй ветви: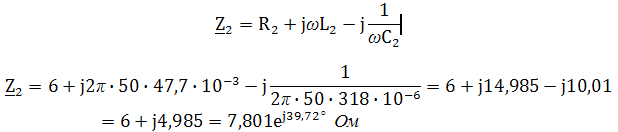



Комплексное сопротивление третьей ветви: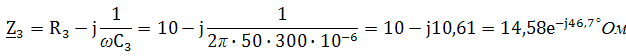



Общее сопротивление цепи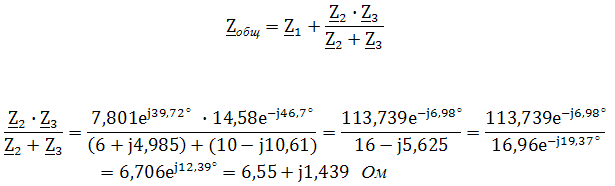



Откуда



— нагрузка носит активно-индуктивный характер

2. Находим действующие значения токов в ветвях: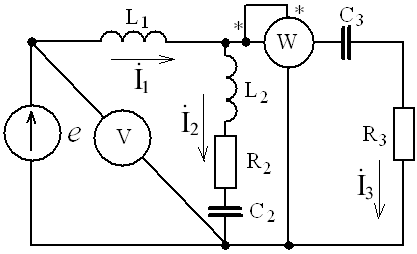

 



Рис.6. Схема с обозначенными комплексными токами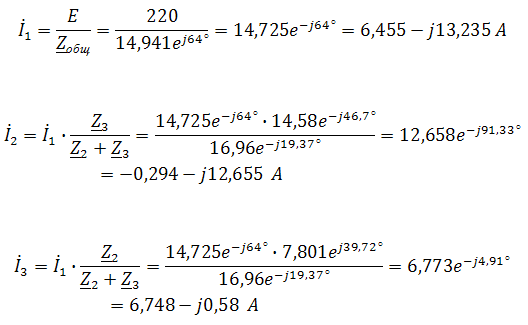



Действующие значения, соответственно,



3. Определим показания приборов:
Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:
U=220 В
Ваттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом,  активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания: