физика. Это тело, размерами которого в условиях данной задачи можно пренебречь
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
Теплопроводность газов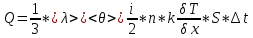 – уравнение теплопроводности/Фурье – уравнение теплопроводности/Фурье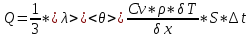 - уравнение теплопроводности/Фурье, где Λ = - уравнение теплопроводности/Фурье, где Λ = 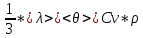 – коэффициент теплопроводности – коэффициент теплопроводностиДиффузия в газах 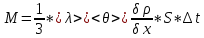 - закон Фика, где D = - закон Фика, где D = 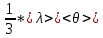 – коэффициент диффузии ( – коэффициент диффузии (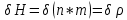 ) )Вязкость газов 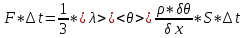  - сила внутреннего трения, где η = - сила внутреннего трения, где η = 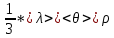 - коэффициент вязкости - коэффициент вязкости3 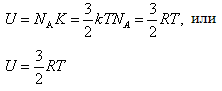 1) Внутренняя энергия термодинамической системы - В термодинамических процессах изменяется только кинетическая энергия движущихся молекул (тепловой энергии недостаточно, чтобы изменить строение атома, а тем более ядра). Следовательно, фактически под внутренней энергией в термодинамике подразумевают энергию теплового хаотического движения молекул. 1) Внутренняя энергия термодинамической системы - В термодинамических процессах изменяется только кинетическая энергия движущихся молекул (тепловой энергии недостаточно, чтобы изменить строение атома, а тем более ядра). Следовательно, фактически под внутренней энергией в термодинамике подразумевают энергию теплового хаотического движения молекул.В 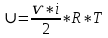 Число степеней свободы молекулы&Закон равномерного распределения энергии по степеням свободы молекул - 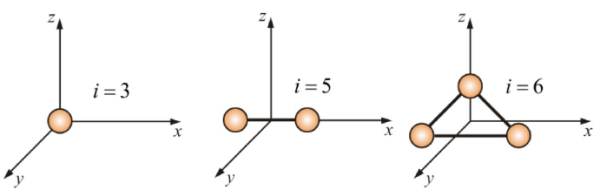    32) Внутренняя энергия идеального газа - Работа газа при изменении его объёма - Если газ, расширяясь, передвигает поршень на расстояние dl, то производит над ним работу dA = Fdl = pS dl = pdV 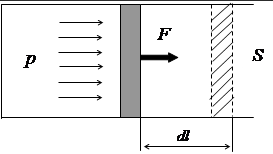 dA = pdV К 3  3) Теплоёмкость – 1. Удельная теплоёмкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1кг вещества на 1К: 3) Теплоёмкость – 1. Удельная теплоёмкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1кг вещества на 1К: 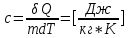 2. Молярная теплоёмкость: 2. Молярная теплоёмкость: 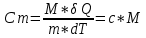 . Теплоёмкость идеального газа при постоянном давлении и при постоянном объёме – . Теплоёмкость идеального газа при постоянном давлении и при постоянном объёме – 1. Изобарный 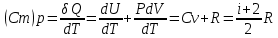 2. Изохорный. В изохорном процессе постоянен объём, то есть  V=0 и, следовательно, газ не совершает работы. Первое Начало Термодинамики для изохорного процесса имеет вид: V=0 и, следовательно, газ не совершает работы. Первое Начало Термодинамики для изохорного процесса имеет вид: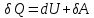 , , 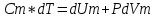 , , 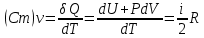 У 34) Применение первого закона термодинамики для вычисления работы и изменения внутренней энергии при изохорическом, изобарическом, изотермическом процессах(см. лист) – 1. При изотермическом процессе изменения внутренней энергии в идеальном газе не происходит и все подводимое к газу количество теплоты идет на совершение им работы: T = const, U = const, ΔU = 0, Q = A. 2. При изохорном процессе объем газа остается постоянным. Соответственно, не совершается работа и внутренняя энергия газа изменяется исключительно за счет теплообмена с окружающей средой: V = const, ΔV = 0, A = 0, ΔU = QV 35) Адиабатический процесс. Уравнение Пуассона. Работа идеального газа при адиабатическом процессе (см листок). 36) Обратимые и необратимые процессы - 1. Обратимым термодинамическим процессом называется термодинамический процесс, допускающий возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Необходимым и достаточным условием обратимости термодинамического процесса является его равновесность (состояние равновесия – то состояние, в котором система может находится бесконечно долго при неизменных внешних параметрах). Квазистатические процессы – текут бесконечно медленно – бесконечная последовательность равновесных состояний, причём может пойти вспять, а потом снова в прежнем направлении. 2. Необратимым термодинамическим процессом называется термодинамический процесс, не допускающий возможности возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Все реальные процессы протекают с конечной скоростью. Они сопровождаются трением, диффузией и теплообменом при конечной разности между температурами системы и внешней среды. Следовательно, все они неравновесны и необратимы. 3. Всякий необратимый процесс в одном направлений (прямом) протекает самопроизвольно, а для осуществления его в обратном направлении так, чтобы система вернулась в первоначальное состояние, требуется компенсирующий процесс во внешних телах, в результате которого состояния этих тел .оказываются отличными от первоначальных. Например, процесс выравнивания температур двух соприкасающихся различно нагретых тел идет самопроизвольно, т. е. не связан с необходимостью одновременного существования каких-либо процессов в других (внешних), телах. Однако для осуществления обратного процесса увеличения разности температур тел до первоначальной нужны компенсирующие процессы во внешних телах, обусловливающие, например, работу холодильной машины. Круговой процесс – цикл, в котором система периодически возвращается в исходное состояние. КПД для кругового процесса – 1. Если за цикл совершается положительная работа A>0: 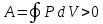 - цикл по часовой стрелке, прямой цикл - цикл по часовой стрелке, прямой цикл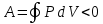 - цикл против часовой стрелки, обратный цикл - цикл против часовой стрелки, обратный циклПричём 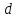 U = 0, так как по кругу => Q = A. Но в результате кругового процесса система может как получать, так и терять теплоту => U = 0, так как по кругу => Q = A. Но в результате кругового процесса система может как получать, так и терять теплоту =>Q = Q1(полученное) – Q2(отданное) КПД = 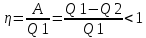 . Прямой цикл – тепловой двигатель (за счёт получения тепла извне), обратный – холодильная машина. . Прямой цикл – тепловой двигатель (за счёт получения тепла извне), обратный – холодильная машина.37) Приведённое количество теплоты - элементарное количество теплоты 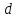 Q, полученное термодинамической системой в бесконечно малом процессе, при абсолютной температуре T. Определяется отношением: Q, полученное термодинамической системой в бесконечно малом процессе, при абсолютной температуре T. Определяется отношением:  . Понятие в термодинамику было введено Клаузиусом. . Понятие в термодинамику было введено Клаузиусом.Р 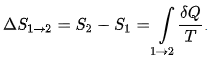 азность энтропий в двух равновесных состояниях 1 и 2, по определению, равна приведённому количеству тепла, которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути азность энтропий в двух равновесных состояниях 1 и 2, по определению, равна приведённому количеству тепла, которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому путиЭ 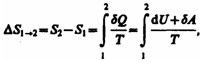 Т п С где k — постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана (57.8) позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия. Так как реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных состояний к более вероятным, до тех пор пока вероятность состояния не станет максимальной. Сопоставляя выражения (57.5) и (57.8), видим, что энтропия и термодинамическая вероятность состояний замкнутой системы могут либо возрастать (в случае необратимых процессов), либо оставаться постоянными (в случае обратимых процессов). Отметим, однако, что эти утверждения имеют место для систем, состоящих из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для «малых» систем могут наблюдаться флуктуации, т. е. энтропия и термодинамическая вероятность состояний замкнутой системы на определенном отрезке времени могут убывать, а не возрастать, или оставаться постоянными 38) Изменение энтропии в законах идеального газа (см вопрос 37). 39) Второй закон термодинамики, его различные формулировки – 1. Второе начало т/д определяет направление протекания т/д процессов 2. Устанавливает существование энтропии как функции состояния термодинамической системы и вводит понятие абсолютной термодинамической температуры, то есть «второе начало представляет собой закон об энтропии» и её свойствах. В изолированной системе энтропия остаётся либо неизменной, либо возрастает (в неравновесных процессах), достигая максимума при установлении термодинамического равновесия (закон возрастания энтропии). 3. По Кельвину: невозможно всё тепло перевести в работу/вечный двигатель второго невозможен из-за невозможности создать тепловой двигатель с КПД = 1. 4. По Клаузису: невозможно передать тепло от более холодного тела к более горячему. 4 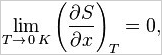 0) Третий закон термодинамики - Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система (где х — любой термодинамический параметр системы (давление, объём и др.)): 0) Третий закон термодинамики - Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система (где х — любой термодинамический параметр системы (давление, объём и др.)):Т Т Для чисто термодинамического подхода достаточно теоремы Нернста. В статистической физике более естественен подход Планка, а теорема Нернста уже не является аксиомой, а получается автоматически, как следствие статистического подхода. 4 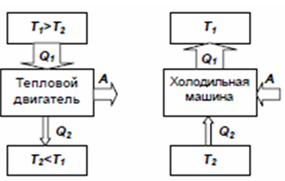 1) Тепловые двигатели и холодильные машины – 1. Тепловой двигатель - это периодически действующий двигатель, совершающий работу за счет полученной извне теплоты. Рабочее тело - это тело, совершающее круговой процесс и обменивающееся энергией с другими телами. Принцип работы теплового двигателя: от термостата с более высокой температурой T1, называемого нагревателем, за цикл отнимается количество теплоты Q1, а термостату с более низкой температурой T2, называемому холодильником, за цикл передается количество теплоты Q2. При этом совершается работа A=Q1-Q2. 1) Тепловые двигатели и холодильные машины – 1. Тепловой двигатель - это периодически действующий двигатель, совершающий работу за счет полученной извне теплоты. Рабочее тело - это тело, совершающее круговой процесс и обменивающееся энергией с другими телами. Принцип работы теплового двигателя: от термостата с более высокой температурой T1, называемого нагревателем, за цикл отнимается количество теплоты Q1, а термостату с более низкой температурой T2, называемому холодильником, за цикл передается количество теплоты Q2. При этом совершается работа A=Q1-Q2.КПД = 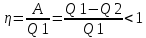 , При этом Q=Q1-Q2=A или Q1=Q2+A. Количество теплоты Q1, отданное системой термостату T1, больше количества теплоты Q2, полученного от термостата T2, на величину работы, совершенной над системой. Эффективность холодильной машины характеризует холодильный коэффициент η' - отношение отнятой от термостата с более низкой температурой количества теплоты Q2 к работе A, которая затрачивается на приведение холодильной машины в действие: , При этом Q=Q1-Q2=A или Q1=Q2+A. Количество теплоты Q1, отданное системой термостату T1, больше количества теплоты Q2, полученного от термостата T2, на величину работы, совершенной над системой. Эффективность холодильной машины характеризует холодильный коэффициент η' - отношение отнятой от термостата с более низкой температурой количества теплоты Q2 к работе A, которая затрачивается на приведение холодильной машины в действие: η'=Q2/A=Q2/(Q1-Q2) Ц 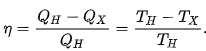 икл Карно и его КПД для идеального газа - это идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов. В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником. икл Карно и его КПД для идеального газа - это идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов. В процессе Карно термодинамическая система выполняет механическую работу за счёт обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры. Резервуар с более высокой температурой называется нагревателем, а с более низкой температурой — холодильником.  |
