физика. Это тело, размерами которого в условиях данной задачи можно пренебречь
 Скачать 1.3 Mb. Скачать 1.3 Mb.
|
|
Раздел физики, который основывается на молекулярно-кинетической теории, называется молекулярной физикой. 2) Термодинамический метод изучает макроскопические свойства веществ и основывается на изучении различных превращений энергии. Раздел физики, в котором физические свойства вещества изучаются с помощью термодинамического метода, называется термодинамикой. Термодинамика основывается на трех фундаментальных законах (началах). Молекулярно-кинетическая теория и термодинамика дополняют друг друга, образуя по существу одно целое. Термодинамическая система и её основные параметры – T, P, V - совокупность макроскопических. тел, к-рые могут взаимодействовать между собой и с др. телами (внеш. средой) — обмениваться с ними энергией и в-вом. Т. с. состоит из столь большого числа структурных ч-ц (атомов, молекул), что её состояние можно характеризовать макроскопическими параметрами: плотностью, давлением, концентрацией в-в, образующих Т. с., и т. д. Термодинамическое состояние и термодинамический процесс – 1) термодинамическое состояние — совокупность макроскопических параметров, характеризующих состояние термодинамической системы. Выбор параметров конкретной термодинамической системы зависит от целей исследования, связь между параметрами носит название уравнения состояния. 2) Термодинамическим процессом называется процесс изменения состояния термодинамического тела (системы), не находящегося в термодинамическом равновесии с внешней средой и не изолированный от нее. При этом наблюдается энергетическое взаимодействие между телом и окружающей средой, сопровождающееся изменением параметров тела. Термодинамическое равновесие - состояние системы, при котором остаются неизменными во времени макроскопические величины этой системы (температура, давление, объём, энтропия) в условиях изолированности от окружающей среды. В общем, эти величины не являются постоянными, они лишь флуктуируют (колеблются) возле своих средних значений. Если равновесной системе соответствует несколько состояний, в каждом из которых система может находиться неопределенно долго, то о системе говорят, что она находится в метастабильном равновесии. 22) Постулаты молекулярно-кинетической теории идеального газа - 1. Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными, т.е. состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы. 2. Атомы и молекулы находятся в непрерывном хаотическом движении. 3. Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало. Процессы, протекающие в идеальном газе при постоянстве одного из термодинамических параметров - 1.Изохорический процесс. Закон Шарля. V = const. И 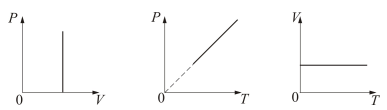 При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным: P/Т = const. 2.Изобарический процесс. Закон Гей-Люссака. Р = const. И 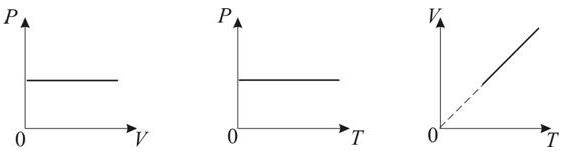 При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре о стаётся постоянным: V/T = const. 3 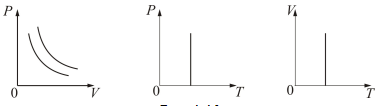 Изотермическим процессом называется процесс, протекающий при постоянной температуре Т. Поведение идеального газа при изотермическом процессе подчиняется закону Бойля – Мариотта: П 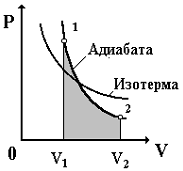 4 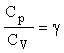 .Адиабатический процесс (изоэнтропийный): .Адиабатический процесс (изоэнтропийный):Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой. 5 О  2 2 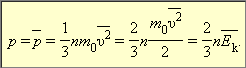 4) Основное уравнение молекулярно-кинетической теории - Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура). По законам механики это изменение импульса всех столкнувшихся со стенкой м 4) Основное уравнение молекулярно-кинетической теории - Простейшей моделью, рассматриваемой молекулярно-кинетической теорией, является модель идеального газа. В кинетической модели идеального газа молекулы рассматриваются как идеально упругие шарики, взаимодействующие между собой и со стенками только во время упругих столкновений. Суммарный объем всех молекул предполагается малым по сравнению с объемом сосуда, в котором находится газ. Модель идеального газа достаточно хорошо описывает поведение реальных газов в широком диапазоне давлений и температур. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, объем, температура). По законам механики это изменение импульса всех столкнувшихся со стенкой мИз уравнения P=n*k*T следует, что при одинаковых температуре и давлении все газы содержат в единице объёма одинаковое количество молекул. Абсолютный нуль температуры. Температура, определяемая формулой (9.6), очевидно, не может быть отрицательной, так как все величины, стоящие в левой части этой формулы, заведомо положительны. Следовательно, наименьшим возможным значением температуры T является значение T=0, если давление p или объем V равны нулю. 2 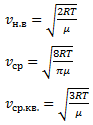 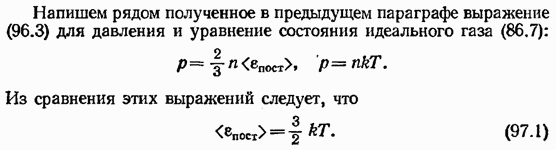 5) Закон Максвелла о распределении молекул идеального газа по скоростям (без вывода) - используя методы теории вероятностей, Максвелл нашел функцию f(v) - закон распределения молекул идеального газа по скоростям: f(v) зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т). Средняя, средняя квадратичная и наиболее вероятная скорости молекул – 5) Закон Максвелла о распределении молекул идеального газа по скоростям (без вывода) - используя методы теории вероятностей, Максвелл нашел функцию f(v) - закон распределения молекул идеального газа по скоростям: f(v) зависит от рода газа (от массы молекулы) и от параметра состояния (от температуры Т). Средняя, средняя квадратичная и наиболее вероятная скорости молекул – 2  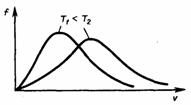 6) Средняя энергия молекул – Закон Максвелла о распределении молекул идеального газа по значениям энергии теплового движения - функция распределения молекул по энергиям теплового движения: 6) Средняя энергия молекул – Закон Максвелла о распределении молекул идеального газа по значениям энергии теплового движения - функция распределения молекул по энергиям теплового движения: 27) Барометрическая формула - зависимость давления или плотности газа от высоты в поле силы тяжести в стационарных условиях. Д 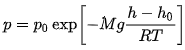 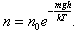 ля идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид. Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону. Распределение Больцмана – если термодинамическая система находящаяся в равновесном состоянии, помещена в силовое поле, то распределение в пространстве молекул описывается распределением Больцмана , где n – концентрация молекул. ля идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид. Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону. Распределение Больцмана – если термодинамическая система находящаяся в равновесном состоянии, помещена в силовое поле, то распределение в пространстве молекул описывается распределением Больцмана , где n – концентрация молекул.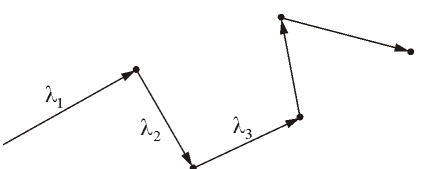 28) Столкновения молекул & Средняя длина свободного пробега молекул & Эффективное сечение молекулы & Цилиндр столкновений & Среднее число столкновений в единицу времени - Расстояние, проходимое молекулой в среднем без столкновений, называется средней длиной свободного пробега. Средняя длина свободного пробега равна ( 28) Столкновения молекул & Средняя длина свободного пробега молекул & Эффективное сечение молекулы & Цилиндр столкновений & Среднее число столкновений в единицу времени - Расстояние, проходимое молекулой в среднем без столкновений, называется средней длиной свободного пробега. Средняя длина свободного пробега равна (М 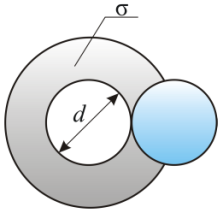 одель идеального газа – твёрдые шарики одного диаметра, взаимодействующие между собой только при столкновении. Обозначим σ – эффективное сечение молекулы, т.е. полное поперечное сечение рассеяния, характеризующее столкновение между двумя молекулами одель идеального газа – твёрдые шарики одного диаметра, взаимодействующие между собой только при столкновении. Обозначим σ – эффективное сечение молекулы, т.е. полное поперечное сечение рассеяния, характеризующее столкновение между двумя молекулами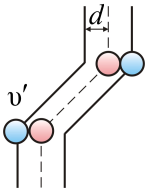  29) Опытное обоснование молекулярно-кинетической теории - Основные положения МКТ подтверждаются многими опытными фактами. Существование молекул, атомов и ионов доказано экспериментально, молекулы достаточно изучены и даже сфотографированы с помощью электронных микроскопов. Способность газов неограниченно расширяться и занимать весь предоставленный им объем объясняется непрерывным хаотическим движением молекул. Упругость газов, твердых и жидких тел, способность жидкостей смачивать некоторые твердые тела, процессы окрашивания, склеивания, сохранения формы твердыми телами и многое другое говорят о существовании сил притяжения и отталкивания между молекулами. Явление диффузии — способность молекул одного вещества проникать в промежутки между молекулами другого — тоже подтверждает основные положения МКТ. Явлением диффузии объясняется, например, распространение запахов, смешивание разнородных жидкостей, процесс растворения твердых тел в жидкостях, сварка металлов путем их расплавления или путем давления. Подтверждением непрерывного хаотического движения молекул является также и броуновское движение — непрерывное хаотическое движение микроскопических частиц, нерастворимых в жидкости. Основными доказательствами этих положений считались: - Диффузия - Броуновское движение - Изменение агрегатных состояний вещества Б 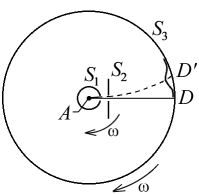 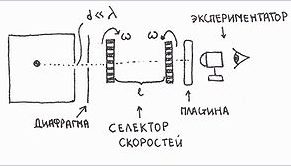 роуновское движение, опыт Штерна, опыт Ламмерта – 1) беспорядочное движение микроскопических видимых, плавающих в жидкости или газе частиц твёрдого вещества, вызываемое тепловым движением частиц жидкости или газа. Броуновское движение является следствием и свидетельством существования теплового движения 2) Проверка того факта, что атомы и молекулы идеальных газов в термически равновесном пучке имеют различные скорости, была осуществлена немецким физиком Отто Штерном (1888-1969) в 1920 г. Таким образом, в этом опыте были не только измерены скорости газовых молекул, но и показано, что они имеют большой разброс по скоростям. Причина – в хаотичности теплового движения молекул. Ещё в XIX веке Дж. Максвелл утверждал, что молекулы, беспорядочно сталкиваясь друг с другом, как-то «распределяются» по скоростям, причём вполне определённым образом 3) физический эксперимент 1929 года, поставленный немецким физиком-эксприментатором Бертольдом Ламмертом для подтверждения распределения Максвелла. В опыте используется ящик с газом, молекулы которого вылетают через отверстие наружу. Диаметр отверстия много меньше длины свободного пробега молекул, молекул в ящике много, так что исчезновение вылетающих не меняет имеющееся распределение по скоростям внутри ящика. Колёса селектора, на поверхности которых находятся выступы, пропускающие или останавливающие летящие молекулы, вращаются с угловой скоростью w. Так, преодолев первое колесо, молекула летит расстояние l до второго, которое за это время поворачивается на угол альфа. Экспериментальное определение числа Авогадро - Броуновское движение указывает на то, что достаточно малые частицы вовлекаются в совершаемое молекулами тепловое движение. Принимая участие в тепловом движении, такие частицы должны вести себя подобно гигантским молекулам, и на них должны распространяться закономерности кинетической теории, в частности закон. роуновское движение, опыт Штерна, опыт Ламмерта – 1) беспорядочное движение микроскопических видимых, плавающих в жидкости или газе частиц твёрдого вещества, вызываемое тепловым движением частиц жидкости или газа. Броуновское движение является следствием и свидетельством существования теплового движения 2) Проверка того факта, что атомы и молекулы идеальных газов в термически равновесном пучке имеют различные скорости, была осуществлена немецким физиком Отто Штерном (1888-1969) в 1920 г. Таким образом, в этом опыте были не только измерены скорости газовых молекул, но и показано, что они имеют большой разброс по скоростям. Причина – в хаотичности теплового движения молекул. Ещё в XIX веке Дж. Максвелл утверждал, что молекулы, беспорядочно сталкиваясь друг с другом, как-то «распределяются» по скоростям, причём вполне определённым образом 3) физический эксперимент 1929 года, поставленный немецким физиком-эксприментатором Бертольдом Ламмертом для подтверждения распределения Максвелла. В опыте используется ящик с газом, молекулы которого вылетают через отверстие наружу. Диаметр отверстия много меньше длины свободного пробега молекул, молекул в ящике много, так что исчезновение вылетающих не меняет имеющееся распределение по скоростям внутри ящика. Колёса селектора, на поверхности которых находятся выступы, пропускающие или останавливающие летящие молекулы, вращаются с угловой скоростью w. Так, преодолев первое колесо, молекула летит расстояние l до второго, которое за это время поворачивается на угол альфа. Экспериментальное определение числа Авогадро - Броуновское движение указывает на то, что достаточно малые частицы вовлекаются в совершаемое молекулами тепловое движение. Принимая участие в тепловом движении, такие частицы должны вести себя подобно гигантским молекулам, и на них должны распространяться закономерности кинетической теории, в частности закон.Основную трудность в опытах Перена составляло приготовления одинаковых частиц и определение их массы. Применив многократно метод центрифугирования, Перрену удалось приготовить весьма однородную эмульсию из практически одинаковых шариков гуммигута[1] с радиусами порядка нескольких десятых долей микрона. Эмульсия помешалась в плоскую стеклянную кювету глубиной 0,1 мм и рассматривалась с помощью микроскопа. Микроскоп имел столь малую глубину поля зрения, что в него были видны только частицы, находящиеся в горизонтальном слое толщиной примерно 1 мк. Перемещая микроскоп в вертикальном направлении, можно было исследовать распределение броуновских частиц по высоте. 30) Явление переноса в термодинамически неравновесных системах - это группа явлений, обусловленных хаотическими движениями молекул и приводящих к направленному переносу: массы(диффузии), энергии (теплопроводимости), импульса 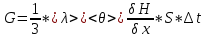 - общее уравнение переноса. - общее уравнение переноса. |
