реферат 3 з-н термодинамики. Формулировка
 Скачать 96 Kb. Скачать 96 Kb.
|
|
Содержание
Введение Третье начало термодинамики (Теорема Нернста): энтропия физической системы при стремлении температуры к абсолютному нулю не зависит от параметров системы и остается неизменной. Тепловой закон Нернста, согласно которому энтропия S любой системы стремится к конечному для неё пределу, не зависящему от давления, плотности или фазы, при стремлении температуры (Т) к абсолютному нулю. Третье начало термодинамики позволяет находить абсолютное значение энтропии, что нельзя сделать на основе первого и второго начал термодинамики. В классической термодинамике (первого и второго начал) энтропия может быть определена лишь с точностью до произвольной аддитивной постоянной S0, что практически не мешает большинству термодинамических исследований, так как реально измеряется разность энтропий (S0) в различных состояниях. Согласно третьему началу термодинамики при Т → 0 значение ΔS → 0. Другие формулировки теоремы: при стремлении температуры к абсолютному нулю все изменения состояния системы не изменяют ее энтропии; при помощи конечной последовательности термодинамических процессов нельзя достичь температуры абсолютного нуля. М. Планк дополнил теорему гипотезой, согласно которой энтропия всех тел при абсолютном нуле температуры равна нулю. Он дал другую формулировку третьего начала термодинамики - как условие обращения в нуль энтропии всех тел при стремлении температуры к абсолютному нулю: Отсюда S0 = 0. Это даёт возможность определять абсолютное значения энтропии и других термодинамических потенциалов. Формулировка Планка соответствует определению энтропии в статистической физике через термодинамическую вероятность (W) состояния системы S = klnW. При абсолютном нуле температуры система находится в основном квантово-механическом состоянии, если оно невырождено, для которого W = 1 (состояние реализуется единственным микрораспределением). Следовательно, энтропия S при Т = 0 равна нулю. В действительности при всех измерениях стремление энтропии к нулю начинает проявляться значительно раньше, чем может стать существенной при T → 0 дискретность квантовых уровней макроскопической системы, приводящая к явлениям квантового вырождения. Из теоремы вытекают важные следствия о свойствах веществ при температурах, близких к абсолютному нулю: приобретают нулевое значение удаленные теплоемкости при постоянных объеме и давлении, термический коэффициент расширения и давления. Кроме того, из теоремы следует недостижимость абсолютного нуля температуры при конечной последовательности термодинамических процессов. Если первое начало термодинамики утверждает, что теплота есть форма энергии, измеряемая механической мерой, и невозможность вечного двигателя первого рода, то второе начало термодинамики объявляет создание вечного двигателя второго рода. Первое начало ввело функцию состояния – энергию, второе начало ввело функцию состояния – энтропию. Если энергия закрытой системы остается неизменной, то энтропия этой системы, состоящая из энтропий ее частей, при каждом изменении увеличивается – уменьшение энтропии считается противоречащим законам природы. Существование таких независимых друг от друга функций состояния, как энергия и энтропия, дает возможность делать высказывания о тепловом поведении тел на основе математического анализа. Поскольку обе функции состояния вычислялись лишь по отношению к произвольно выбранному начальному состоянию, определения энергии и энтропии не были совершенными. Третье начало термодинамики позволило установить этот недостаток. Важное значение для развития термодинамики имели установленные Ж.Л. Гей-Люссаком законы – закон теплового расширения и закон объемных отношений. Б.Клапейрон установил зависимость между физическими величинами, определяющими состояние идеального газа (давлением, объемом и температурой), обобщенное Д.И. Менделеевым. Таким образом, концепции классической Термодинамики описывают состояния теплового равновесия и равновесные (протекающие бесконечно медленно, поэтому время в основные уравнения не входит) процессы. Термодинамика неравновесных процессов возникает позднее - в 30-х гг.ХХ века. В ней состояние системы определяется через плотность, давление температуру и другие локальные термодинамические параметры, которые рассматриваются как функции координат и времени. Определение Третье начало термодинамики (теорема Нернста) – физический принцип, определяющий поведение энтропии при приближении температуры к абсолютному нулю. Является одним из постулатов термодинамики, принимаемым на основе обобщения значительного количества экспериментальных данных. Формулировка Третье начало термодинамики может быть сформулировано так: «Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система». или 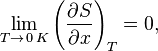 где Третье начало термодинамики относится только к равновесным состояниям. Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение): третье начало термодинамики может быть использовано для точного определения энтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю. Третье начало термодинамики позволяет находить абсолютное значение энтропии, что нельзя сделать в рамках классической термодинамики (на основе первого и второго начал термодинамики). В классической термодинамике энтропия может быть определена лишь с точностью до произвольной аддитивной постоянной В 1911 году Макс Планк сформулировал третье начало термодинамики как условие обращения в нуль энтропии всех тел при стремлении температуры к абсолютному нулю: Следствия Недостижимость абсолютного нуля температур:Из третьего начала термодинамики следует, что абсолютного нуля температуры нельзя достичь ни в каком конечном процессе, связанном с изменением энтропии, к нему можно лишь асимптотически приближаться, поэтому третье начало термодинамики иногда формулируют как принцип недостижимости абсолютного нуля температуры. Поведение термодинамических коэффициентов: Из третьего начала термодинамики вытекает ряд термодинамических следствий: при |

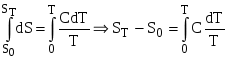
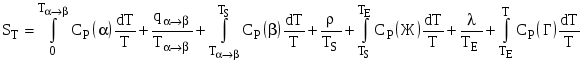 , (5.15)
, (5.15)