Лекция шар Математика. Лекция Шар_03052021. Лекция Сфера и шар. Площади сферы и ее частей. Объемы шара и его частей
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Лекция _ 03.05.2021 Лекция «Сфера и шар. Площади сферы и ее частей. Объемы шара и его частей» 1  . Понятие «Шар и сфера» . Понятие «Шар и сфера»Определение:Сферой называется поверхность, состоящая из всех точек пространства, которые расположены на данном расстоянии от данной точки. Основные элементы: 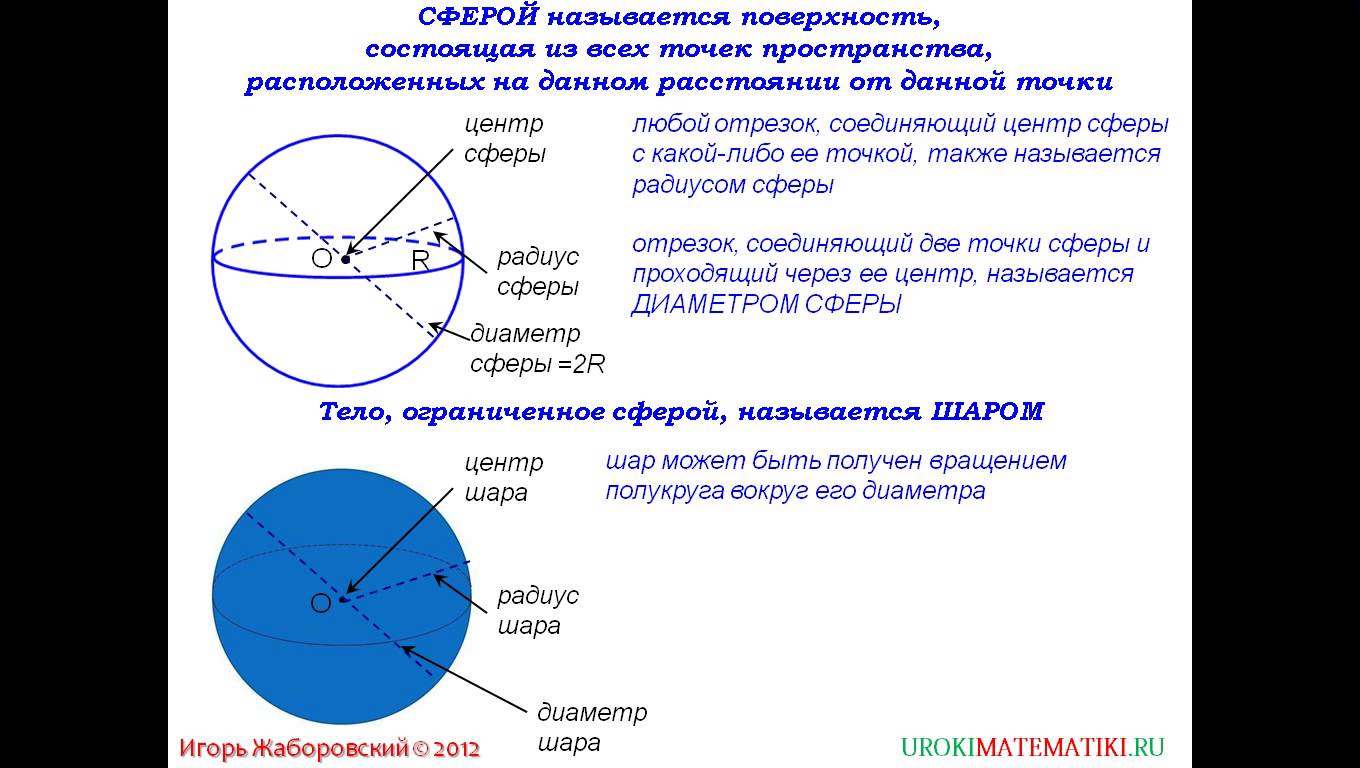 Данная точка О – центр сферы. Данное расстояние – радиус сферы (R). Радиус сферы – любой отрезок, соединяющий центр и какую-нибудь точку сферы. Диаметр сферы (D) – отрезок, соединяющий две точки сферы и проходящий через ее центр. D = 2R. Сфера может быть получена вращением полуокружности вокруг ее диаметра. 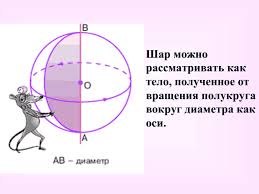 Определение: Шаром называется тело, ограниченное сферой. Основные элементы: 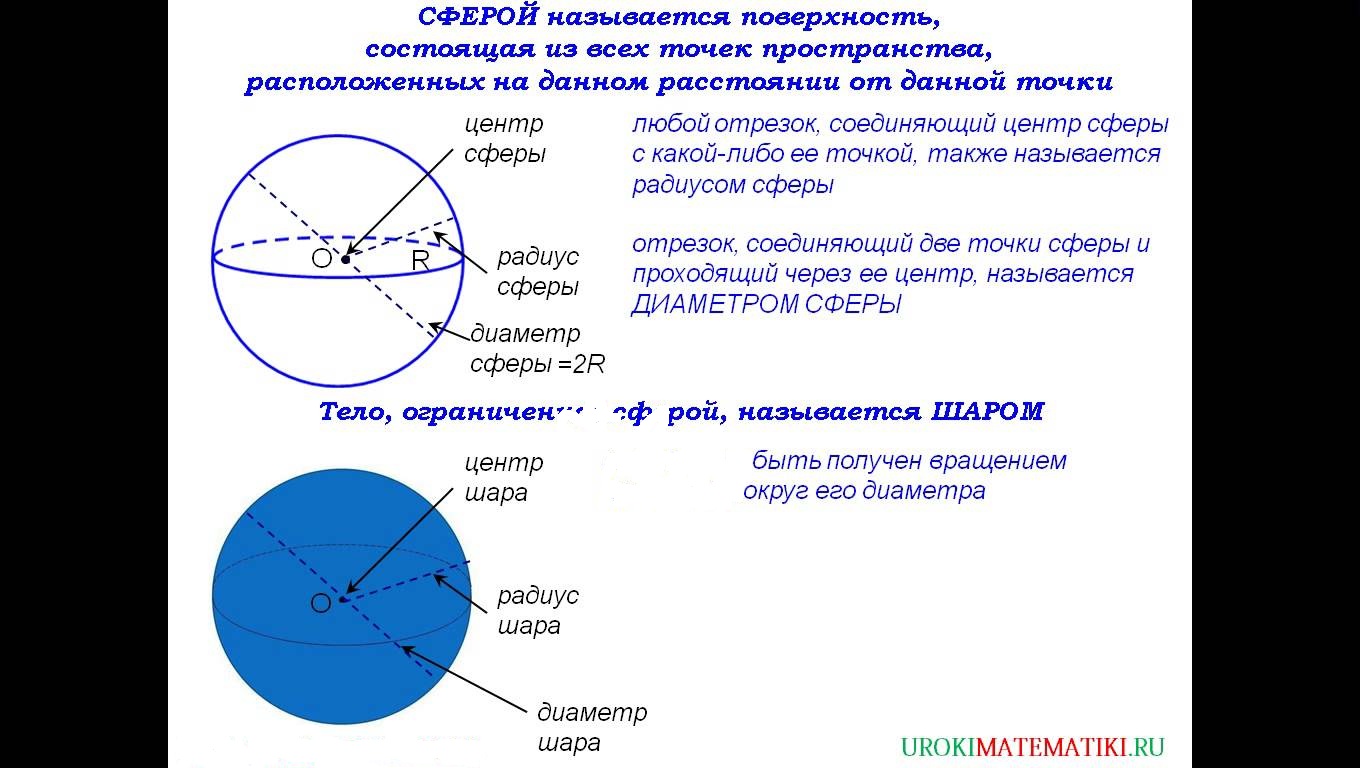 Радиус шара (R) – любой отрезок, соединяющий центр и какую-нибудь точку сферы. Диаметр шара (D) – отрезок, соединяющий две точки сферы и проходящий через ее центр. D = 2R. Центр шара – точка О. 2. Формулы: Теорема 1: Площадь сферы радиуса R равен:  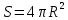 , ,где 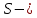 площадь сферы; площадь сферы;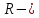 радиус сферы. радиус сферы.Теорема 2: Объем шара радиуса R равен:  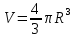 , ,где 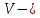 объём шара; объём шара;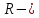 радиус шара. радиус шара.3. Части шара и формулы.
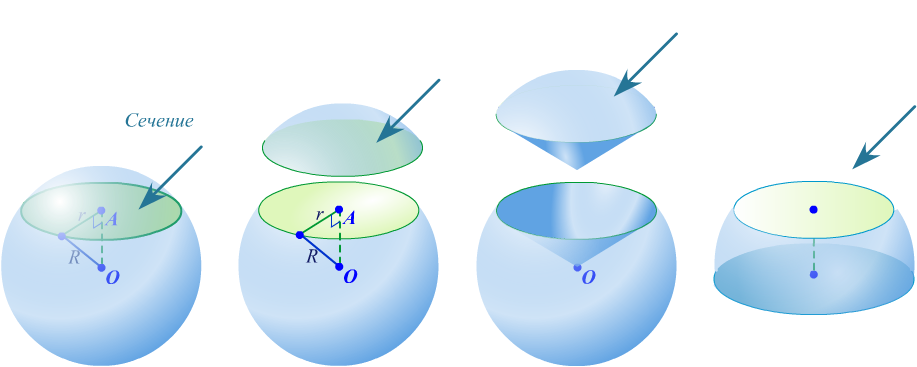
4. Сечения В 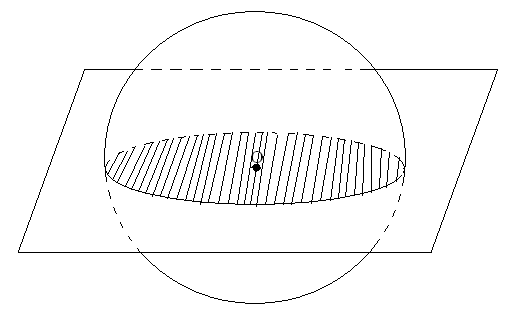 сякое сечение шара плоскостью есть круг. Плоскость, проходящая через центр шара называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы- большой окружностью. сякое сечение шара плоскостью есть круг. Плоскость, проходящая через центр шара называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы- большой окружностью.Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии. Определение. Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью. Точка А называется точкой касания. Т 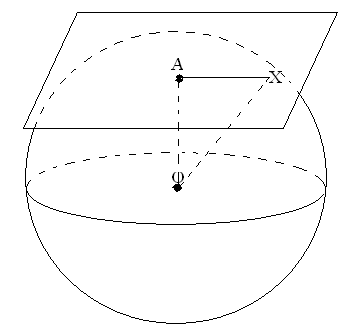 еорема. Касательная плоскость имеет с шаром только одну общую точку- точку касания. еорема. Касательная плоскость имеет с шаром только одну общую точку- точку касания.Прямая в касательной плоскости шара, проходящая через точку касания, называется касательной к шару в этой точке. Так как касательная плоскость имеет с шаром только одну общую точку, то касательная прямая тоже имеет с шаром только одну общую точку- точку касания. Теорема. Линия пересечения двух сфер есть окружность. 5. Закрепление изученного материала А1) Найти площадь поверхности сферы, радиуса 5 см. А2) Найти площадь поверхности сферы, с диаметром 40 см. А3) Найти радиус сферы, площадь поверхности которой равна 256 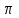 см2. см2.В1) Найти площадь поверхности сферы, образованной полуокружностью, длина которой 12 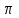 см2. см2. | |||||||||||||||||||||||||||||||||||||||


 Части шара
Части шара
 часть шара отсекаемая от него какой-нибудь плоскостью
часть шара отсекаемая от него какой-нибудь плоскостью
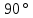 , вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов
, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов
 часть шара, заключенная
часть шара, заключенная 

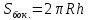 ,
, 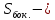 площадь сегментовой поверхности шара;
площадь сегментовой поверхности шара;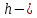 высота сегмента
высота сегмента
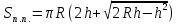 ,
,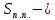 площадь полной поверхности шарового сектора;
площадь полной поверхности шарового сектора;
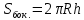 ,
,  Объем шарового сегмента:
Объем шарового сегмента: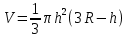 ,
,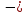 объем шарового сегмента;
объем шарового сегмента; Объем шарового сектора:
Объем шарового сектора: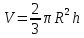 ,
,  Объем шарового слоя:
Объем шарового слоя: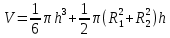 ,
,