Курсовая по основам мат.моделирования. Факультет машиностроения и аэрокосмической техники кафедра технологии машиностроения
 Скачать 358.89 Kb. Скачать 358.89 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Воронежский государственный технический университет» (ФГБОУ ВО «ВГТУ» ВГТУ) ФАКУЛЬТЕТ МАШИНОСТРОЕНИЯ И АЭРОКОСМИЧЕСКОЙ ТЕХНИКИ КАФЕДРА ТЕХНОЛОГИИ МАШИНОСТРОЕНИЯ Курсовая работа по дисциплине Основы математического моделирования Обучающийся _____________Неделин Михаил Андреевич_______________ (Ф.И.О. обучающегося) Группа _______бКТО-201____________________________________________ Тема Выбор заготовки для изготовления детали вал из 5 альтернатив по 11 критериям методом анализа иерархий__________________ _________________________________________________________________ Обучающийся _____________________М.А. Неделин ____________ (подпись, И.О.Фамилия, дата) Проверила __________________________доцент А.В. Перова___________ (подпись, И.О.Фамилия,дата) Оценка ___________________________ Воронеж 2021СОДЕРЖАНИЕВоронеж 2021 1 Введение 3 1.Постановка задачи для метода анализа иерархий 5 1.1. Формирование матрицы попарных сравнений 8 1.2. Формирование матриц попарных сравнений для третьего уровня 11 1.3. Синтез глобальных приоритетов 16 2.Методы линейного программирования в математическом моделировании технологических процессов 18 2.1.Задача и исходные данные 18 2.2.Составление целевой функции и ограничений 18 2.3.Решение задачи средствами Excel 19 Заключение 21 СПИСОК ЛИТЕРАТУРЫ 22 Приложение А 23 Введение 3 1. Постановка задачи для метода анализа иерархий 5 1.1. Формирование матрицы попарных сравнений 8 1.2. Формирование матриц попарных сравнений для третьего уровня 11 1.3. Синтез глобальных приоритетов 16 2. Методы линейного программирования в математическом моделировании технологических процессов 18 2.1. Задача и исходные данные 18 2.2. Составление целевой функции и ограничений 18 2.3. Решение задачи средствами Excel 19 Заключение 21 СПИСОК ЛИТЕРАТУРЫ 22 Приложение А 23 ВведениеМетод анализа иерархий (МАИ) является математической процедурой для иерархического представления сущностных элементов на все более простые составляющие части и дальнейшей обработке последовательных суждений оценщика по парным сравнениям. Главное преимущество метода анализа иерархий заключается в возможности сравнивать критерии и варианты решений попарно, что существенно облегчает обоснование сделанных выводов. Анализ проблемы принятия решений начинается с построения иерархической структуры, которая включает цель, критерии, альтернативы и другие рассматриваемые факторы, влияющие на выбор. Эта структура отражает понимание проблемы лицом, принимающим решение. Каждый элемент иерархии может представлять различные аспекты решаемой задачи, причем во внимание могут быть приняты как материальные, так и нематериальные факторы, измеряемые количественные параметры и качественные характеристики, объективные данные и субъективные экспертные оценки. Иными словами, анализ ситуации выбора решения в МАИ напоминает процедуры и методы аргументации, которые используются на интуитивном уровне. Следующим этапом анализа является определение приоритетов, представляющих относительную важность или предпочтительность элементов построенной иерархической структуры, с помощью процедуры парных сравнений. Безразмерные приоритеты позволяют обоснованно сравнивать разнородные факторы, что является отличительной особенностью МАИ. На заключительном этапе анализа выполняется синтез (линейная свертка) приоритетов на иерархии, в результате которой вычисляются приоритеты альтернативных решений относительно главной цели. Лучшей считается альтернатива с максимальным значением приоритета. Существо симплекс-метода состоит в следующем: 1. Находят какое-либо допустимое базисное решение. Его можно найти, приняв какие-либо n - m переменных за свободные, приравняв их к нулю и решив полученную систему уравнений. Если при этом некоторые из базисных переменных окажутся отрицательными, то нужно выбрать другие свободные переменные, т.е. перейти к новому базису. 2. Проверяют, не достигнут ли уже максимум (минимум) целевой функции при найденном допустимом базисном решении. 3. Если оптимальное решение не найдено, то ищут новое допустимое базисное решение, но не любое, а такое, которое увеличивает (уменьшает) значение целевой функции. При пользовании табличным методом удобно ввести специальную форму записи уравнений и целевой функции в виде матрицы коэффициентов при свободных переменных. Решение задачи линейного программирования табличным методом заключается в нахождении на первом этапе какого-либо допустимого базисного решения, которое в общем случае не является оптимальным, и преобразовании первоначальной матрицы коэффициентов с целью перехода к лучшему базисному решению. Для более полного представления о задаче линейного программирования дают ее геометрическую интерпретацию. Проводят геометрическое построение прямых или плоскостей (в зависимости от числа уравнений и неизвестных), соответствующих каждому уравнению системы, вершины образовавшейся фигуры будут соответствовать набору допустимых базисных решений. Постановка задачи для метода анализа иерархий Валы предназначены для передачи вращающего момента и, как правило, поддержания установленных на них деталей. Кроме вращающих моментов валы нагружены обычно поперечными силами и изгибающими моментами. Различают валы прямые и коленчатые, ступенчатые и гладкие, сплошные и пустотелые, цельные и составные, а также гибкие проволочные. Чаще всего валы выполняют ступенчатыми, состоящими из участков различных диаметров, называемых монтажными шейками и служащих для установки на них различных деталей. Крепление деталей на валах во избежание проворота осуществляется с помощью шпонок, шлицев, штифтов и клиньев, а для предотвращения осевого перемещения - втулками, запорными кольцами, винтами и прочее. Технические требования к валам: отсутствие износа, забоин и задиров монтажных шеек; наличие заданных размеров и правильной геометрической формы монтажных шеек; перпендикулярность опорных уступов и буртиков осп вала; прямолинейность оси вала и отсутствие его скрученности; отсутствие трещин, изломов; отсутствие износа и смятия рабочих поверхностей шлицев, шпоночных пазов, резьбы. Необходимо выбрать заготовку для изготовления детали «вал» (Приложение А). Исходя из технических требований в результате обсуждений удалось определить 11 критериев, уточняющих эту цель. Задача заключается в выборе одной из 5 заготовок, технические характеристики которых указаны в таблице 1. Соответствующая нисходящая иерархическая декомпозиция представлена на рисунке 1. Таблица 1 – Характеристики заготовок
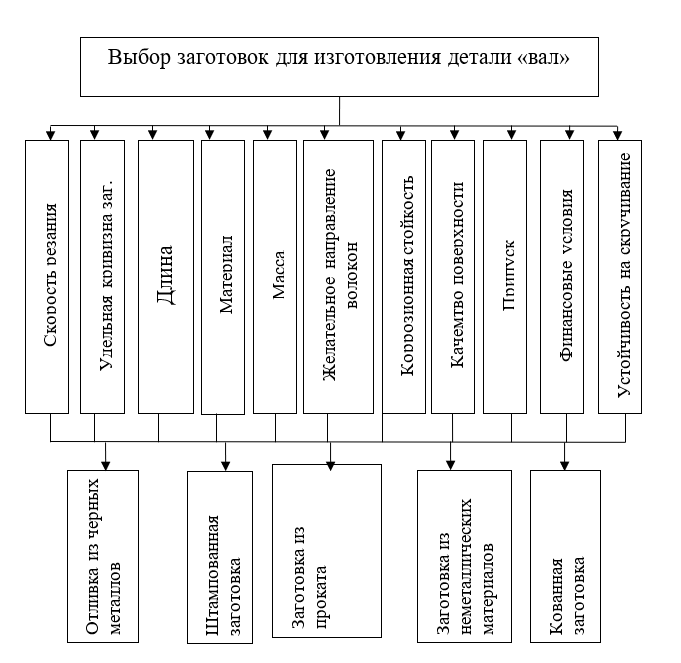 Рисунок 1 - Формирование иерархии 1.1. Формирование матрицы попарных сравненийВ рамках МАИ с участием ЛПР формируется матрица попарных сравнений элементов на основе субъективных суждений, численно оцениваемых по определенной шкале. На основе выраженных численно результатов попарных сравнений потом решается задача нахождения абсолютных весов. В идеале, при полной согласованности суждений матрица попарных сравнений имеет вид рисунке 2. 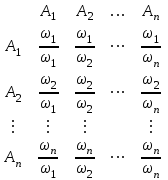 Рисунок 2 - Матрица попарных сравнений при согласованности суждений Матрица попарных сравнений составляется для сравнения относительной важности критериев на втором уровне по отношению к общей цели управления. Далее составляются аналогичные матрицы для попарных сравнений альтернатив по каждому из критериев. Для проведения парных сравнений разработана шкала относительной важности, представленная в таблице 2. Таблица 2 – Шкала относительной важности
Продолжение таблицы 2
В данной задаче требуется сформировать двенадцать матриц: одну для второго уровня и одиннадцать – для третьего уровня (по числу введенных критериев второго уровня). Матрица попарных сравнений для второго уровня представлена в таблице 3. Таблица 3 – Матрица попарных сравнений
1.2. Формирование матриц попарных сравнений для третьего уровняДалее составляется 11 матриц попарных сравнений для выбора пяти заготовок по каждому критерию. Для этого дается описание заготовок, представленное в таблице 1. Матрицы попарных сравнений представлены на рисунках 3-13.  Рисунок 3 - Скорость резания Рисунок 3 - Скорость резания Рисунок 4 - Удельная кривизна заготовки Рисунок 4 - Удельная кривизна заготовки Рисунок 5 - Длина Рисунок 5 - Длина Рисунок 6 - Материал Рисунок 6 - Материал Рисунок 7 - Масса Рисунок 7 - Масса Рисунок 8 - Желательное направление волокон Рисунок 8 - Желательное направление волокон Рисунок 9 - Коррозионная стойкость Рисунок 9 - Коррозионная стойкость Рисунок 10 - Качество поверхности Рисунок 10 - Качество поверхности Рисунок 11 - Припуск Рисунок 11 - Припуск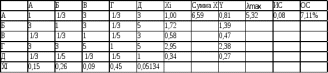 Рисунок 12 - Финансовые условия Рисунок 12 - Финансовые условия Рисунок 13 - Устойчивость на скручивание Рисунок 13 - Устойчивость на скручиваниеПроведем расчеты по матрице попарных сравнений для второго уровня: Определяем геометрическое среднее элементов строк матриц по формуле: 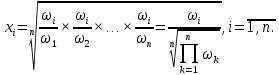 (1) (1)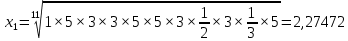 Аналогично, по выше представленной формуле (1), определяем геометрическое среднее каждой матрицы: 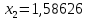 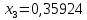 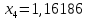 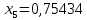 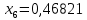 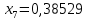 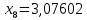 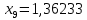 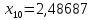 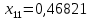 После нормализации вектора 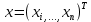 получаем вектор приоритетов: получаем вектор приоритетов: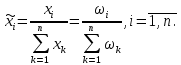 (2) (2)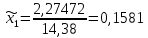 Аналогично, по выше представленной формуле (2), определяем вектор приоритетов каждой матрицы: 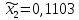 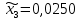 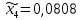 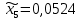 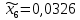 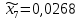 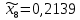 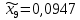 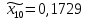 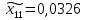 Умножаем матрицу А на вектор 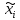 : :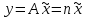 , (3) , (3)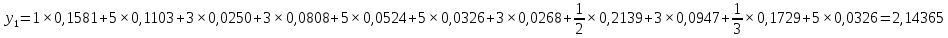 Аналогично, по выше представленной формуле (3), определяем yi каждой матрицы: 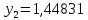 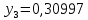 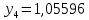 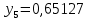 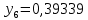 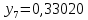 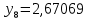 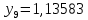 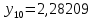 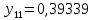 Рассчитываем параметр 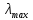 по формуле: по формуле: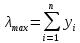 (4) (4)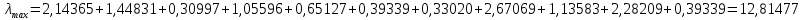 Рассчитываем индекс согласованности по формуле: 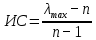 (5) (5)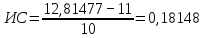 Рассчитываем отношение согласованности по формуле: 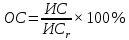 , (6) , (6)где 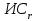 индекс согласованности, получаемый при усреднении множества данных для матриц попарных сравнений при случайном равновероятном (то есть полностью неосмысленном) выборе количественных значений суждений из шкалы 1/10, 1/9,…, 9, 10, но с сохранением свойства обратной симметрии. индекс согласованности, получаемый при усреднении множества данных для матриц попарных сравнений при случайном равновероятном (то есть полностью неосмысленном) выборе количественных значений суждений из шкалы 1/10, 1/9,…, 9, 10, но с сохранением свойства обратной симметрии.Значения 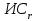 приведены в таблице 4. приведены в таблице 4.Таблица 4 – Значение 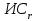
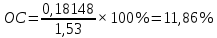 , (7) , (7)Величина 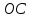 считается приемлемой, если она имеет значения порядка 20% и менее. Если считается приемлемой, если она имеет значения порядка 20% и менее. Если 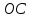 выходит из этих пределов, то можно рекомендовать лицам, формулирующим суждения, пересмотреть их с использованием дополнительной информации. выходит из этих пределов, то можно рекомендовать лицам, формулирующим суждения, пересмотреть их с использованием дополнительной информации.В данной матрице величина ОС считается приемлемой. Остальные матрицы рассчитываются аналогично первой. 1.3. Синтез глобальных приоритетовВо всех матрицах получились приемлемые значения величины ОС, так как не превысили 20%. После того как получены достаточно согласованные оценки на различных уровнях и их локальные приоритеты, в МАИ осуществляется синтез глобальных приоритетов. Для этого по каждой 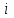 -ой альтернативе вычисляется величина -ой альтернативе вычисляется величина 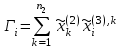 , (8) , (8)где 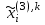 компонент вектора локальных приоритетов компонент вектора локальных приоритетов 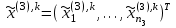 для для 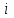 -ой альтернативы третьего (нижнего) уровня относительно -ой альтернативы третьего (нижнего) уровня относительно 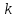 -го критерия верхнего (второго на рис. 1) уровня; -го критерия верхнего (второго на рис. 1) уровня; 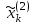 компонент вектора приоритетов компонент вектора приоритетов 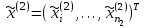 критериев второго уровня; критериев второго уровня; 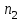 , , 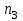 количество элементов, выделенных в иерархии на втором и третьем уровнях. количество элементов, выделенных в иерархии на втором и третьем уровнях.В таблице 5 приведены итоговые результаты определения приоритетов выбора для различных уровней и полученные глобальные приоритеты. Таблица 5 – Значения глобальных приоритетов 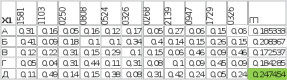 Альтернатива, имеющая наивысший глобальный приоритет, будет являться оптимальным вариантом. В нашем случае наивысший глобальный приоритет ГП=0,247454 имеет заготовка под буквой Д (кованная), следовательно, этот заготовка будет являться самым лучшим вариантом для изготовления детали «вал». Вывод: Методом анализа иерархий удалось выбрать оптимальную заготовку–кованная, так как у нее был наивысший приоритет по таким критериям как: скорость резания, удельная кривизна заготовки, длина, материал, масса, желательное направление волокон, коррозионная стойкость, качество поверхности, припуск, финансовые условия и устойчивость на скручивание. Методы линейного программирования в математическом моделировании технологических процессовЗадача и исходные данныеВариант 16 Предприятие производит три вида продукции (А, В, С), для выпуска каждого из которых требуется определенное время обработки на всех четырех типах оборудования ОБ1, ОБ2, ОБ3 и ОБ4.
Пусть время работы оборудования составляет соответственно 84, 42, 21 и 42 ч. Определите какую продукцию и в каких количествах следует производить, чтобы предприятие получило максимальную прибыль. Составление целевой функции и ограничений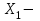 количество продукции А количество продукции А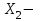 количество продукции В количество продукции В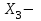 количество продукции С количество продукции СЦелевая функция: 3X1+6X2+4X3 →Mах Ограничения: Х1+6Х2+3Х3 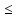 84; 84;3Х1+Х2+3Х3 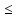 42; 42; Х1+3Х2+2Х3 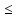 21; 21; 2Х1+3Х2+4Х3 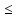 42; 42; X1≥0; X2≥0; X3≥0. Решение задачи средствами ExcelВ ячейках (E4;Е10) запишем команду «=СУММПРОИЗВ($B$3:$D$3;B4:D4)» согласно рисунку 14. 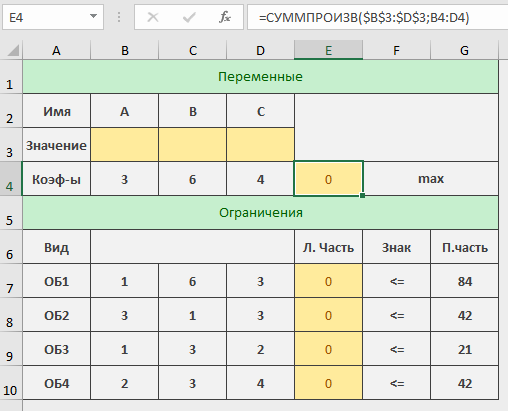 Рисунок 14 – Решение задачи После того, как мы заполнили нужные ячейки, переходим в раздел «данные» и нажимаем «поиск решения». Откроется окно, как показано на рисунке 15. В поле «оптимизировать целевую функцию» указываем ячейку целевой функции Е4. Ставим найти максимум. В поле «изменяя ячейки» указываем те ячейки, где будут выводиться значения конечного продукта каждого вида (B3 и D3). В поле «в соответствии с ограничениями» добавляем наши ограничения. Выбираем метод решения «Поиск решения линейных задач симплекс-методом» и нажимаем найти решения. 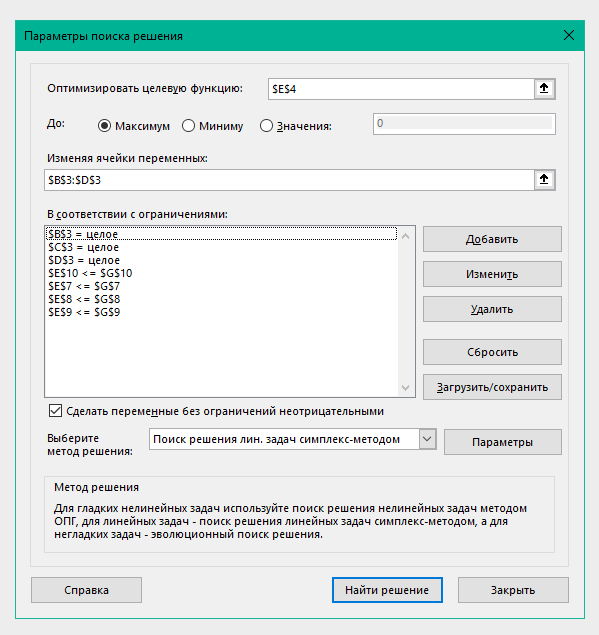 Рисунок 15 – Решение задачи В итоге получаем значения, которые показаны на рисунке 16. 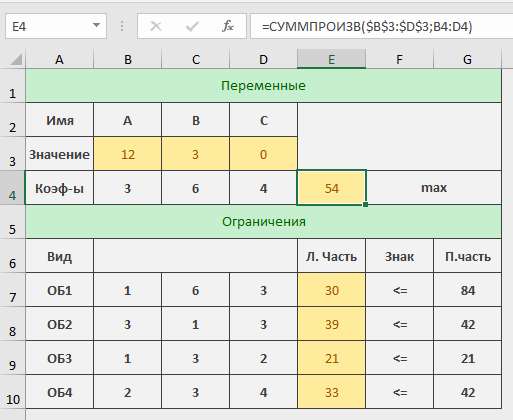 Рисунок 16 – Решение задачи Вывод: Для того, чтобы получить максимальную прибыль (54), нужно изготавливать 12 единиц продукции А и 7 единиц продукции В, для этого будет затрачено 30 часа на оборудовании 1, 39 часов на оборудовании 2, 21 час на оборудовании 3 и 31 час на оборудовании 4. ЗаключениеВ ходе курсовой работы было решено две задачи. Первая задача состояла в выборе заготовки для изготовления детали «вал». Методом анализа иерархий удалось выбрать оптимальную заготовку–кованная, так как у нее был наивысший приоритет по таким критериям как: скорость резания, удельная кривизна заготовки, длина, материал, масса, желательное направление волокон, коррозионная стойкость, качество поверхности, припуск, финансовые условия и устойчивость на скручивание. Вторая задача – задача линейного программирования состояла в определении максимальной прибыли предприятия. Задача была решена с использованием средств Excel. В итоге для того, чтобы получить максимальную прибыль (54), нужно изготавливать 12 единиц продукции А и 7 единиц продукции В, для этого будет затрачено 30 часа на оборудовании 1, 39 часов на оборудовании 2, 21 час на оборудовании 3 и 31 час на оборудовании 4. СПИСОК ЛИТЕРАТУРЫАверченков В.И. Основы математического моделирования технических систем / В.И. Аверченков, В.П. Федоров, М.Л. Хейфец. – Лань, 2011. Аврамчук Е.Ф. Технология системного моделирования / Е.Ф. Аврамчук, А.А. Вавилов, С.В. Емельянов. – М.: Машиностроение, 1988. Вентцель Е.С. Исследование операций. Задачи, принципы, методология: учеб. пособие для вузов / Е.С. Вентцель. – М.: Дрофа, 2004. Гельман В.Я. Решение математических задач средствами Excel: практикум / В.Я. Гельман. – СПб.: Питер, 2003. Пантелеев А.В. Методы оптимизации в примерах и задачах: учеб. пособие / А.В. Пантелеев, Т.А. Летова. – М.: Высш. шк., 2002. Перова А.В. Основы математического моделирования: курс лекций: учеб. пособие / А.В. Перова. Воронеж: ФГБОУ ВО «Воронежский государственный технический университет», 2016. Перова А.В. Основы математического моделирования: учеб. пособие / А.В. Перова. Воронеж: ГОУ ВПО «Воронежский государственный технический университет», 2010. Приложение А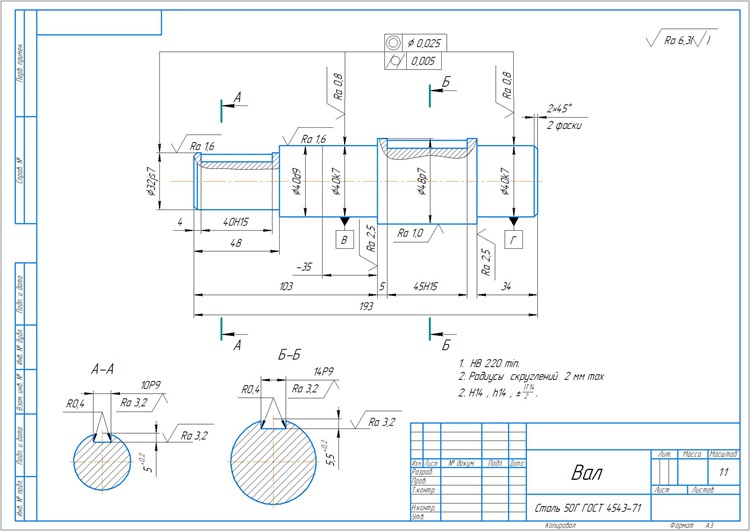 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
