Тест по теории вероятностей. Федеральное агентство по образованию Государственное образовательное учреждение

• Название: Федеральное агентство по образованию Государственное образовательное учреждение
• Анкор: Тест по теории вероятностей
• Дата: 31.05.2021
• Размер: 0.58 Mb.
• Имя файла: TeoriaVer.doc
• Тип: Задача; #212097
• страница: 5 из 5

Вариант №23

1. 
   Брошены две игральные кости. Какова вероятность, что сумма выпавших очков не менее 9?
   
2. 
   Из последовательности чисел 1,2,…,100 наудачу выбираются 2 числа. Какова вероятность, что одно из них меньше 30, а другое больше 30?
   
3. 
   В прямоугольник с вершинами (-3; -1), (3; -1), (3; 1), (-3; 1) случайно брошена точка .Какова вероятность того, что она окажется внутри эллипса ?
   
4. 
   В урне N белых шаров и M черных. Надуачу извлекается K шаров (K>M).Какова вероятность того, что в урне остались только белые шары?
   
5. 
   В ящике в случайном порядке разложено двадцать деталей, причем пять из них стандартные. Рабочий берет наудачу три детали. Найти вероятность того, что, по крайней мере, одна из этих деталей окажется стандартной.
   
6. 
   В первой урне имеется 3 белых и 2 черных шара, во второй 4 белых и 6 черных. Шары отличаются только цветом. Из каждой урны достают по одному шару. Какова вероятность, что они окажутся одного цвета?
   
7. 
   Бросаются одновременно две игральные кости. Найти вероятность того, что произведение выпавших очков будет четным.
   
8. 
   Два автомата штампуют однотипные детали. Производительность второго вдвое больше первого. Первый дает 2№ брака, второй 1%. Найти вероятность того, что взятая наудачу с конвейера деталь окажется бракованной.
   
9. 
   В специализированную больницу поступают в среднем 50% больных с заболеванием К, 30% с заболеванием L, 20% с заболеванием М. Вероятность полного излечения болезни К равна 0,7; для болезни L и M эти вероятности соответственно равны0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найти вероятность того, что этот больной страдал заболеванием К.
   
10. 
    Вероятность того, что малое предприятие за год станет банкротом равна 0,2. Найти вероятность того, что из 10 малых предприятий за год сохранятся хотя бы два.
    
11. 
    Вероятность неточной сборки прибора равна 0,1. Найти вероятность того, что среди 900 приборов окажется от 750 до 850 точных.
    
12. 
    Игральный шестигранный кубик подбрасывается 500 раз. Какова вероятность того, что отклонение относительной частоты появления шестерки от вероятности ее появления в одном опыте по абсолютной величине не превзойдет 0,1?
    
13. 
    Определить надежность схемы, если P_i – надежность i – го элемента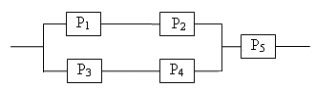
    

Вариант №24

1. 
   В лифт девятиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятности следующих событий:
   
2. 
   Бросаются четыре игральные кости. Найти вероятность того, что на них выпадет по одинаковому числу очков.
   
3. 
   В квадрат с вершинами в точках (0,0), (0,1), (1,1), (1,0) наудачу брошена точка (х,у). Найдите вероятность того, что координаты этой точки удовлетворяют неравенству у<2х.
   
4. 
   В урне «а» белых шаров и «в» черных (а>2). Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми?
   
5. 
   На складе имеются 8 изделий, 3 из них изготовлены заводом N. Найтивероятность того, что среди 4 наудачу взятых изделий окажется не более половины, изготовленных заводом N.
   
6. 
   На карточках написаны цифры 2,3,4,5,6,7,8,9. Наудачу берут две карточки. Какова вероятность, что обе выбранные цифры нечетные.
   
7. 
   В связке имеется 6 ключей, из которых только один подходит к двери. Найти вероятность того, что на открывание потребуется не более четырех опробований. Предполагается, что опробованный ключ в дальнейших опробованиях не участвует.
   
8. 
   В урне содержится 7 черных и 3 белых шара. Из урны наудачу достают два шара и перекладывают во вторую урну. После этого из второй урны наудачу достают один шар. Найти вероятность того, что он белый.
   
9. 
   Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны ; ; .
   
10. 
    Найти вероятность того, что при 5 бросаниях монеты число появлений герба будет больше числа появлений решек.
    
11. 
    Вероятность появления события в каждом из независимых испытаний равна 0,5. Найти число испытаний , при котором с вероятностью 0,9973 можно ожидать, что относительная частота появления события отклониться от его вероятности по абсолютной величине не более, чем на 0,02.
    
12. 
    Вероятность появления события в каждом из независимых испытаний равна 0,9. Сколько нужно произвести испытаний, чтобы с вероятностью не меньшей 0,8 можно было ожидать, что отклонение относительной частоты от вероятности появления события в одном испытании равной 0,9 не превзойдет 0,2.
    
13. 
    Определить надежность схемы, если P_i – надежность i – го элемента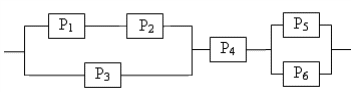
    

Вариант №25

1. 
   Из букв слова «ротор», составленного из букв разрезной азбуки, наудачу последовательно извлекаются 3 буквы и складываются в ряд. Какова вероятность того, что получится слово «тор».
   
2. 
   Бросают два игральных кубика. Найти вероятность того, что сумма очков, выпавших на этих кубиках, равна 8.
   
3. 
   На отрезок АВ длиной 12 см наугад ставят точку М. Найдите вероятность того, что площадь квадрата, построенного на отрезке АМ, будет между 36 см² и 81 см².
   
4. 
   Студент знает 30 из 40 вопросов программы. Найти вероятность того, что студент знает 2 вопроса, содержащиеся в его экзаменационном билете.
   
5. 
   Среди 6 лотерейных билетов 2 выигрышных. Наудачу берут два билета. Какова вероятность того, что среди них окажется:
   

а) один выигрышный;

б) два выигрышных.

6. 
   В лотерее 100 билетов из которых 20 выигрышных. Участник покупает два билета. Определить вероятность того, что хотя бы один билет будет выигрышным.
   
7. 
   На карточках написаны цифры 4,5,7,8,9. Наудачу берут две карточки. Какова вероятность, что обе выбранные цифры окажутся нечетными?
   
8. 
   По самолету производится два выстрела, вероятность попадания при каждом из них равна 0,6. При одном попадании самолет будет сбит с вероятностью 0,5, при двух – с вероятностью – 0,9. Какова вероятность того, что самолет будет сбит.
   
9. 
   В ящик, где 10 деталей 1-го сорта и 3 детали 2-го сорта, токарь положил одну изготовленную деталь. После чего сборщик взял наудачу из ящика одну деталь, которая оказалась первого сорта. Найти вероятность того, что вложенная токарем деталь была 2-ого сорта, если он изготавливает детали только 1-го и 2-го сортов с вероятностями 0,95 и 0,5 соответственно.
   
10. 
    Вероятность рождения мальчика равна 0,515. Найти вероятность того, что из 20 новорожденных будет 11 мальчиков.
    
11. 
    Всхожесть семян ржи составляет 90%. Найти вероятность того, что из 10000 посеянных семян взойдет 900.
    
12. 
    Для данного стрелка вероятность попадания в мишень при одном выстреле равна 0,9. Произведено 1000 выстрелов по мишени. Найти вероятность того, что число попаданий будет менее 80 и не более 95.
    
13. 
    Определить надежность схемы, если P_i – надежность i – го элемента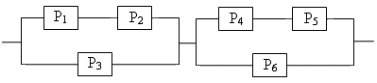
    

Вариант №26

1. 
   На пяти карточках написаны цифры 1,2,3,4,5. Две из них, одна за другой, вынимаются. Найти вероятность того, что число на второй карточке будет больше, чем на первой.
   
2. 
   Вероятность того, что в течение одной смены возникает неполадка станка, равна 0,1. Найти вероятность того, что не пройдет ни одной неполадки за три смены.
   
3. 
   Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 10 см. На плоскость наудачу бросается монета радиуса 2 см. Найти вероятность того, что монета не пересечет ни одной из прямых.
   
4. 
   В урне 7 белых шаров и 3 черных. Наудачу достают 2 шара. Какова вероятность того, что они разного цвета.
   
5. 
   В ящике имеется 5 красных шаров и 3 синих, шары отличаются только цветом. Наудачу достают два шара. Найти вероятности того, что оба шара окажутся:
   

а) одного цвета;

б) разного.

6. 
   Из ящика, где 12 деталей 1 категории и 20 деталей второй категории, наудачу без возвращения извлекли 2 детали. Найти вероятность того, что вторая деталь 1 категории.
   
7. 
   Радист трижды вызывает корреспондента. Причем следующий вызов производится при условии, что предыдущий вызов не принят. Вероятность принятия первого вызова равна 0,3, второго – 0,4, третьего – 0,5. Найти вероятность того, что вызов будет принят.
   
8. 
   По самолету производится 3 выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором – 0,6, при третьем – 0,8. При одном попадании самолет сбивается с вероятностью 0,3, при двух – с вероятностью – 0,6 и при трех – сбивается наверняка. Найти вероятность того, что самолет сбит.
   
9. 
   Из урны, содержащей 7 белых и 12 черных шаров, наудачу без возвращения извлекли 2 шара. Что вероятнее: первый извлеченный шар был белым или черным, если известно, что второй извлеченный шар оказался белым.
   
10. 
    Электронная система состоит из 28 блоков, каждый из которых может отказать в течение года с вероятностью 0,05. Найти наиболее вероятное число отказов и его вероятность.
    
11. 
    Вероятность изготовления бракованного генератора автомобильного двигателя равна 0,0003. Определить вероятность того, что в изготовленной партии из 200 шт. окажется хотя бы один бракованный.
    
12. 
    Вероятность появления события в каждом из независимых опытов равна 0,95. Найти вероятность того, что событие появится не менее 1800 раз в 2000 опытах.
    
13. 
    Определить вероятность разрыва цепи, если P_i – вероятность выхода из строя i – го элемента
    

Вариант №27

1. 
   Какова вероятность того, что в выбранном наудачу двухзначном числе цифры: а) одинаковые; б) различные.
   
2. 
   Бросают два игральных кубика. Найти вероятность того, что сумма очков, выпавших на этих кубиках, не превзойдет 6.
   
3. 
   Каждое их двух чисел неотрицательно, но меньше 2. Найти такие два числа, сумма которых не больше 2,5, а произведение больше 4.
   
4. 
   В урне 5 белых шаров, 3 черных и 6 красных. Наудачу достают 5 шаров. Какова вероятность того, что в выборку попадут 2 белых, 2 черных и 1 красный шар.
   
5. 
   В урне 8 шаров: 3 белых и 5 черных. Какова вероятность того, что вынутые наугад два шара окажутся:
   

а) белые;

б) черные;

в) одного цвета.

6. 
   Из урны, содержащей 5 шаров с номерами от 1 до 5, последовательно извлекаются два шара, причем первый шар возвращается, если номер не равен единице. Определить вероятность того, что шар с номером два будет извлечен при втором извлечении.
   
7. 
   Два игрока поочередно бросают монету. Выигрывает тот, кто первым получит герб. Найти вероятность выигрыша для первого игрока.
   
8. 
   На сборку поступают детали с трех автоматов. Известно, что первый автомат дает 0,3 брака, второй – 0,2, третий – 0,4. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000 деталей, со второго – 2000, с третьего – 2500.
   
9. 
   Вся продукция проверяется двумя контролерами. Вероятность того, что изделие попадет на проверку к первому контролеру, равна, 0,55, а ко второму – 0,45. Вероятность пропустить нестандартные изделия для первого контролера равна 0,01, для второго – 0,02. Взятое наудачу изделие с маркой «стандарт» оказалось бракованным. Какова вероятность, что изделие проверялось вторым контролером?
   
10. 
    В ходе аудиторской проверки компании аудитор случайным образом отбирает 5 счетов. Найти вероятность того, что обнаружит 1 счет с ошибкой, если ошибки содержат в среднем 3% счетов.
    
11. 
    Вероятность появления события в каждом из независимых испытаний равна 0,7. Найти вероятность того, что при 400 испытаниях событие появится 300 раз.
    
12. 
    Сто станков работают независимо друг от друга. Вероятность бесперебойной работы каждого из них в течение смены равна 0,8. Найти вероятность того, что в течение данной смены безотказно поработают 85 станков.
    
13. 
    Определить вероятность разрыва цепи, если P_i – надежность i – го элемента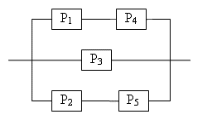
    

Вариант №28

1. 
   Буквенный замок содержит в общей оси 4 диска, каждый из которых разделен на 6 секторов с различными нанесенными на них буквами. Замок открывается в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Определить вероятность того, что замок откроется, если установлена произвольная комбинация букв.
   
2. 
   Бросают два игральных кубика. Найти вероятность того, что произведение выпавших очков равно 8.
   
3. 
   На окружности выбрана некоторая точка А, через которую проводится случайная хорда. Какова вероятность, что длина хорд будет больше стороны правильного вписанного шестиугольника?
   
4. 
   В корзине 12 белых теннисных мячей, 10 красных и 6 синих. Наудачу достают два мяча. Какова вероятность, что они окажутся одного цвета?
   
5. 
   В ящике 10 деталей, среди которых 5 бракованных. Наудачу достают 3 детали. Найти вероятность следующих событий:
   

а) все детали окажутся годными;

б) две детали окажутся годными и одна бракованная.

6. 
   Вероятность успешной попытки выполнить упражнение для каждого из двух спортсменов равна 0,5. Спортсмены упражнение выполняют по очереди, причем каждый делает по две попытки. Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами.
   
7. 
   Какова вероятность, что наудачу выбранное пятизначное число содержит только нечетные цифры?
   
8. 
   Рабочий работает на 3-х станках, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго – 0,03, для третьего – 0,04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего в два раза меньше чем второго. Определить вероятность того, что взятая наудачу деталь будет бракованной.
   
9. 
   В ремесленном цехе трудятся 3 мастера и 6 их учеников. Мастер допускает брак при изготовлении изделия с вероятностью 0,05; ученик – с вероятностью 0,15. Поступившее из цеха изделие оказалось бракованным. Какова вероятность, что его изготовил мастер?
   
10. 
    В среднем 20% акций на аукционе продается по первоначально заявленной стоимости .Найти вероятность того, что из 10 пакетов акций в результате торгов будут проданы не менее двух пакетов акций.
    
11. 
    Завод отправил на базу 1000 изделий. Вероятность повреждения изделий в пути 0,002. Найти вероятность того, что в пути будет повреждено не более трех изделий.
    
12. 
    Отдел технического контроля проверяет 475 изделий на брак. Вероятность того, что изделие бракованное, равна 0,05. Найти с вероятностью 0,9426 границы, в которых будет заключено число бракованных изделий среди проверенных.
    
13. 
    Определить вероятность разрыва цепи, если P_i – вероятность выхода из строя i – го элемента
    

Вариант №29

1. 
   На карточках написаны цифры 1,2,3,4,5. Наудачу достают две карточки. Какова вероятность, что сумма цифр на них будет четной?
   
2. 
   Бросают два игральных кубика. Найти вероятность того, что произведение выпавших очков четное.
   
3. 
   Какова вероятность того, что сумма двух наугад взятых положительных чисел, каждое из которых не больше единицы, не превзойдет единицы, а их произведение больше 2/9?
   
4. 
   Партия из 15 деталей содержит 3 бракованные. Контролер для проверки наудачу берет 5 деталей. Если среди отобранных деталей не будет обнаружено бракованных деталей, то партия принимается. Найти вероятность того, что данная партия будет принята.
   
5. 
   Из урны, содержащей 5 белых шаров и 5 черных, наудачу достают 6 штук. Найти вероятность того, что среди вынутых шаров окажется одинаковое число черных и белых (шары отличаются только цветом).
   
6. 
   Рабочий обслуживает четыре станка. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,7, для второго станка эта вероятность равна 0,8, для третьего – 0,9, для четвертого – 0,85. Найти вероятность того, что в течение часа по крайней мере один станок потребует к себе внимания рабочего.
   
7. 
   Двадцать экзаменационных билетов содержат по два вопроса, которые не повторяются. Экзаменующийся выучил 35 вопросов. Определить вероятность того, что экзамен будет сдан, если для этого нужно ответить на два вопроса билета или на один вопрос билета и один дополнительный вопрос из другого билета.
   
8. 
   По самолету было произведено три выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором – 0,6, при третьем – 0,8. При одном попадании самолет сбивается с вероятностью 0,8, при двух с вероятностью – 0,6, при трех – сбивается наверняка. Найти вероятность того, что самолет сбит.
   
9. 
   В данный район изделия поставляются двумя фирмами в соотношении 5:8. Среди продукции первой фирмы стандартные изделия составляют 90%, второй – 85%. Взятое наугад изделие оказалось стандартным. Найти вероятность того, что оно изготовлено первой фирмы.
   
10. 
    В 10% случаев страховая компания выплачивает по договорам страховку. Найти вероятность того, что по истечение срока 10 договоров компания уплатит страховку в 2 случаях.
    
11. 
    Вероятность получения бракованной детали равна 0,01. Какова вероятность того, что среди 400 деталей бракованных окажется:
    

а) 3 детали;

б) хотя бы одна.

12. 
    Шестигранный игральный кубик подбрасывают 400 раз. Найти вероятность того, что тройка появится не менее 60 и не более 80 раз.
    
13. 
    Определить вероятность разрыва цепи, если P_i – вероятность выхода из строя i – го элемента
    

Вариант №30

1. 
   На карточках написаны цифры 1,2,3,4,5,6,7. Наудачу взяли две карточки. Какова вероятность, что одно число будет меньше трех, а другое больше трех?
   
2. 
   Устройство секретного замка включает в себя 4 ячейки. В первой ячейке осуществляется набор одной из четырех букв A, B, C, D, в трех остальных – одной из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (цифры могут повторяться). Чемуравнавероятность того, что замок будет открыт с первой попытки?
   
3. 
   На отрезке АВ длины l поставлена наудачу точка М. Какова вероятность того, что расстояние этой точки от середины отрезка меньше, чем расстояние этой точки до ближайшего края.
   
4. 
   В ящике 12 красных и 4 синих пуговиц. Вынимают наугад две пуговицы. Какова вероятность того, что пуговицы будут одноцветными?
   
5. 
   В ящике лежат 10 красных, 8 синих и 5 зеленых шаров; шары отличаются только цветом. Наудачу вынимают два шара. Какова вероятность того, что оба вынутых шара окажутся одного цвета?
   
6. 
   Рабочий обслуживает три станка, вероятность того, что в течение часа для первого станка не потребуется помощь рабочего равна 0,9, для второго – 0,8, для третьего – 0,7. Найти вероятность того, что, по крайней мере, для двух станков не потребуется помощь рабочего.
   
7. 
   Вероятность попадания в мишень для данного стрелка равна 0,7. Стрелок делает два выстрела по мишени. Найти вероятности следующих событий:
   

а) стрелок попадет 2 раза;

б) попадет один раз;

в) попадет хотя бы один раз.

8. 
   Заготовки поступают из двух бункеров: 70% из первого и 30-% из второго. При этом материал первого бункера имеет 10% брака, а второго – 20%. Какова вероятность того, что наудачу взятая заготовка бракованная.
   
9. 
   Вся продукция проверяется двумя контролерами. Вероятность того, что изделие попадет на проверку к первому контролеру, равна, 0,35, а ко второму – 0,65. Вероятность пропустить нестандартные изделия для первого контролера равна 0,03, для второго – 0,01. Взятое наудачу изделие с маркой «стандарт» оказалось бракованным. Какова вероятность, что изделие проверялось первым контролером?
   
10. 
    Вероятность того, что пассажир опоздает к поезду, равна 0,01. Найти наиболее вероятное число опоздавших из 500 пассажиров.
    
11. 
    Отдел технического контроля проверяет 900 изделий на стандартность. Вероятность брака равна 0,1. Найти вероятность того, что в данной партии окажется не более 50 бракованных деталей.
    
12. 
    Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти число испытаний , при котором с вероятностью 0,9876 можно ожидать, что относительная частота появления события отклоняется от его вероятности по абсолютной величине не более чем на 0,04.
    
13. 
    Определить надежность схемы, если P_i – отказ i – го элемента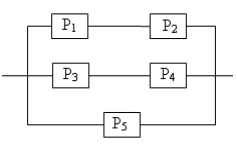
    

1 1. Данко П. Е., Попов А. Г., Кожевникова Т. Я., Высшая математика в упражнениях и задачах. В 2 ч. М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и образование», 2003.

2. Кремер Н. Теория вероятностей и математическая статистика: Учебник 2-е изд. Издательство: ЮНИТИ-ДАНА, 2006.