Тест по теории вероятностей. Федеральное агентство по образованию Государственное образовательное учреждение
 Скачать 0.58 Mb.
|
|
Вариант №16 Бросают два игральных кубика. Найти вероятность того, что сумма очков, выпавших на этих кубиках, равна 8. Брошены две игральные кости. Какова вероятность, что сумма выпавших очков не менее 9? Точка брошена в круг радиуса R. Найдите вероятность того, что она попадает внутрь данного вписанного квадрата. Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что два наудачу выбранных билета окажутся выигрышными. В урне N белых шаров и M черных. Надуачу извлекается K шаров (K>M).Какова вероятность того, что в урне остались только белые шары? В урне 7 белых шаров, 3 черных и 2 красных. Наудачу достают два шара. Найти вероятность того, что они оба окажутся одного цвета. В лотерее 100 билетов из которых 20 выигрышных. Участник покупает два билета. Определить вероятность того, что хотя бы один билет будет выигрышным. Рабочий работает на 3-х станках, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго – 0,03, для третьего – 0,04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего в два раза меньше чем второго. Определить вероятность того, что взятая наудачу деталь будет бракованной. Число грузовых машин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина. В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика, б) не более двух мальчиков, в) более двух мальчиков, г) не менее двух и не более трех мальчиков. Принять вероятность рождения мальчика равной 0,51. Произведено 800 испытаний, вероятность появления события в одном опыте равна 0,8. Вычислить вероятность неравенства  .Вероятность появления события в каждом из 400 испытаний равна 0,2. Найти вероятность того, что отклонение относительной частоты появления события от его вероятности по абсолютной величине не превзойдет 0,05. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента 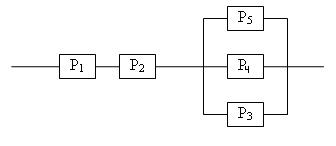 Вариант №17 Вероятность того, что в течение одной смены возникает неполадка станка, равна 0,1. Найти вероятность того, что не пройдет ни одной неполадки за три смены. В лифт девятиэтажного дома на первом этаже вошли 3 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятности следующих событий: А – все пассажиры выйдут на одном этаже. В – все пассажиры выйдут на разных этажах. Расстояние от пункта А до В автобус проходит за 2 мин, а пешеход — за 15 мин. Интервал движения автобусов 25 мин. Вы подходите в случайный момент времени к пункту А и отправляетесь в В пешком. Найдите вероятность того, что в пути вас догонит очередной автобус. У распространителя имеется 20 билетов книжной лотереи, среди которых 7 выигрышных. Куплено 3 билета. Найтивероятность того, что хотя бы один из купленных билетов выигрышный. В урне «а» белых шаров и «в» черных (а>2). Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми? В лотерее 100 билетов, из которых 10 выигрышных. Участник покупает три билета. Определить вероятность того, что хотя бы один билет будет выигрышным. На карточках написаны цифры 2,3,4,5,6,7,8,9. Наудачу берут две карточки. Какова вероятность, что обе выбранные цифры нечетные. По самолету было произведено три выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором – 0,6, при третьем – 0,8. При одном попадании самолет сбивается с вероятностью 0,8, при двух с вероятностью – 0,6, при трех – сбивается наверняка. Найти вероятность того, что самолет сбит. Две перфораторщицы набили на перфораторах по одному комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй перфораторщицы эта вероятность равна 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. Предполагается ,что оба перфоратора были исправны. Монету подбрасывают 100 раз. Найти наивероятнейшее число появлений герба и вероятность такого результата. Вероятность появления события в каждом из независимых испытаний равна 0,4. Найти наименьшее число испытаний при котором с вероятностью 0,9 можно ожидать, что относительная частота появления события отклонится от вероятности его по абсолютной величине не более, чем на 0,01 (применить интегральную теорему Лапласа). Произведено 800 испытаний, вероятность появления события в одном опыте равна 0,8. Вычислить вероятность неравенства .Определить вероятность разрыва цепи, если Pi – надежность i – го элемента 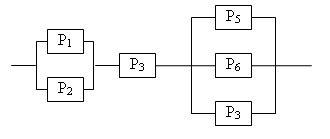 Вариант №18 Какова вероятность, что наудачу взятое трехзначное число будет четным? Из букв слова «ротор», составленного из букв разрезной азбуки, наудачу последовательно извлекаются 3 буквы и складываются в ряд. Какова вероятность того, что получится слово «тор». Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу брошена монета радиуса г < а. Найдите вероятность того, что монета не пересечет ни од ной из прямых. В ящике лежат 11 одинаковых по форме пуговицы, из них: 5 черных пуговиц. Работнице требуется пришить к очередному пальто 4 черные пуговицы. Определить вероятность того, что среди наугад взятых 4 пуговиц все пуговицы черные. Студент знает 30 из 40 вопросов программы. Найти вероятность того, что студент знает 2 вопроса, содержащиеся в его экзаменационном билете. Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,9; для второго и третьего орудий эти вероятности соответственно равны 0,5 и 0,8. Найти вероятность того, что а) только один снаряд попадет в цель; б) все три снаряда попадут в цель. В первой урне имеется 3 белых и 2 черных шара, во второй 4 белых и 6 черных. Шары отличаются только цветом. Из каждой урны достают по одному шару. Какова вероятность, что они окажутся одного цвета? Заготовки поступают из двух бункеров: 70% из первого и 30-% из второго. При этом материал первого бункера имеет 10% брака, а второго – 20%. Какова вероятность того, что наудачу взятая заготовка бракованная. Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед. Вероятность появления события А в каждом опыте равна 0,3. Опыт повторяется 5 раз. Найти вероятность того, что событие появляется не более 2 раз. Монету подбрасывают 900 раз. Найти вероятность того, что герб выпадет: а) 400 раз, б) не менее 400 раз, в) не менее 400 и не более 500 раз. Вероятность появления события в каждом из независимых испытаний равна 0,4. Найти наименьшее число испытаний при котором с вероятностью 0,9 можно ожидать, что относительная частота появления события отклонится от вероятности его по абсолютной величине не более, чем на 0,01 (применить интегральную теорему Лапласа). Определить вероятность разрыва цепи, если Pi – надежность i – го элемента 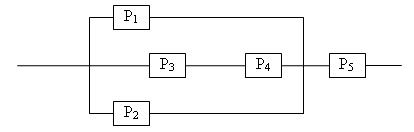 Вариант №19 На карточках написаны цифры 1,2,3,4,5. Наудачу достают две карточки. Какова вероятность, что сумма цифр на них будет четной? По  ячейкам случайно распределяются предметов. Найти вероятность, что все предметы попадут в одну ячейку.На паркет, составленный из правильных треугольников со стороной а, случайно брошена монета радиуса г. Найдите вероятность того, что монета не заденет границы ни одного из треугольников. Партия из 15 деталей содержит 3 бракованные. Контролер для проверки наудачу берет 5 деталей. Если среди отобранных деталей не будет обнаружено бракованных деталей, то партия принимается. Найти вероятность того, что данная партия будет принята. Ящике лежат одинаковые по форме пуговицы: 6 черных и 5 белых. Работнице требуется пришить к очередному пальто 3 черные пуговицы. Определить вероятность того, что среди наугад взятых 5 пуговиц имеется нужное количество черных пуговиц. На карточках написаны цифры 1,2, … , 20. Наудачу берут две карточки. Найти вероятность того, что одна выбранная цифра меньше 10, а вторая больше 10. Покупатель приобрел пылесос и полотер. Вероятность того, что пылесос не выйдет из строя в течение гарантийного срока, равна 0,95, для полотера такая вероятность равна 0,9. Найти вероятность того, что а) оба прибора выдержат гарантийный срок; б) хотя бы один выдержит гарантийный срок. В тире имеется три ружья, вероятности попадания из которых равны соответственно 0,5; 0,6; 0,7. Найти вероятность попадания при одном выстреле, если стреляющий берет одно из ружей наудачу. Известно, что 5% мужчин и 0,25 всех женщин дальтоники. Наудачу выбранное лицо – дальтоник. Какова вероятность того, что это мужчина? (считать, что мужчин и женщин одинаковое количество). Найти вероятность того, что при пяти подбрасываниях игрального кубика единица появляется хотя бы один раз. Вероятность появления события в каждом из 400 испытаний равна 0,2. Найти вероятность того, что отклонение относительной частоты появления события от его вероятности по абсолютной величине не превзойдет 0,05. Оценить вероятность того, что появление герба в 500 испытаниях будет не менее 200 и не более 300 раз. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента 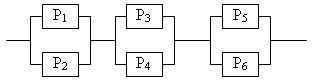 Вариант №20 Ребенок играет с четырьмя буквами разрезной азбуки А, А, М, М. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «МАМА»? Три предмета распределяются по 5 ячейкам случайным образом. Найти вероятность того, что все они попадут в разные ячейки. Стержень длиной  наудачу разломан на З части. Найдите вероятность того, что длина каждой части окажется больше  .Имеется пять билетов стоимостью по одному рублю, три билета по три рубля и два билета по пять рублей. Наугад берутся три билета. Определить вероятность того, что а) все три билета стоят вместе семь рублей, б) все три билета стоимостью по одному рублю. Студент из 15 вопросов знает ответы только на 7 вопросов. Определить вероятность того, что из 5 наугад выбранных вопросов он знает ответы на 3 вопроса. Экзаменационный билет содержит три вопроса. Вероятность того, что студент ответит на любой вопрос билета, равна 0,9. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на два вопроса билета. Рабочий обслуживает три станка, вероятность того, что в течение часа для первого станка не потребуется помощь рабочего равна 0,9, для второго – 0,8, для третьего – 0,7. Найти вероятность того, что, по крайней мере, для двух станков не потребуется помощь рабочего. В каждой из двух урн по 6 черных и 4 белых шара. Из первой урны наудачу извлекли шар и переложили во вторую. Найти вероятность того, что взятый после этого наудачу шар из первой урны окажется белым. В урне находится один шар, о котором известно, что он либо белый, либо черный. В урну положили белый шар, а потом после тщательного перемешивания вынули наудачу один шар, который оказался белым. Какова вероятность того, что после этого вынут из урны белый шар? Вероятность попадания в мишень хотя бы один раз при двух выстрелах для данного стрелка равна 0,99. Найти вероятность попадания в мишень данным стрелком при одном выстреле. Вероятность появления события в одном испытании равна 0,8. Сколько нужно произвести испытаний, чтобы с вероятностью 0,95 можно было ожидать отклонение относительной частоты появления события от его вероятности не более, чем на 0,05. Вероятность появления события в одном опыте равна 0,9. Произведено 900 опытов. Найти наивероятнейшее число появлений события и вероятность такого результата. Определить вероятность разрыва цепи, если Pi – надежность i – го элемента  Вариант №21 Числа 1,2,3,4,5 написаны на пяти карточках. Наугад последовательно выбираются три карточки и располагаются в порядке появления слева направо. Найти вероятность того, что полученное при этом трехзначное число будет четным. Лотерея выпущена на общую сумму N р. Цена одного билета  р. Ценные выигрыши попадают на  билетов. Определите вероятность ценного выигрыша на один билет.Найдите вероятность того, что сумма двух наудачу взятых чисел из отрезка [-1, 1] больше нуля, а их произведение отрицательно. В лотерее N билетов, из которых M выигрышных. Участник купил k билетов. Какова вероятность того, что он ни по одному билету не выиграет? В группе 25 студентов из них 5 отличников. Какова вероятность того, что среди 7 наугад выбранных по списку студентов 3 отличника. Рабочий обслуживает три станка. Вероятность того, что в течение часа для первого станка потребуется внимание рабочего, равна 0,3, для второго – эта вероятность равна 0,2, для третьего – 0,15. Какова вероятность того, что 1) для всех трех станков потребуется внимание рабочего, 2) ни для одного не потребуется внимания. Рабочий обслуживает четыре станка. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,7, для второго станка эта вероятность равна 0,8, для третьего – 0,9, для четвертого – 0,85. Найти вероятность того, что в течение часа по крайней мере один станок потребует к себе внимания рабочего. В сосуд, содержащий 3 одинаковых по форме шара, брошен белый шар. После этого наудачу достают один шар. Какова вероятность того, что шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров по цвету. Урна содержит  шаров. Все предположения о числе белых шаров в урне равновозможны. Наудачу выбранный из урны шар оказался белым. Вычислить вероятность всех предположений о составе шаров в урне. Какое предположение наиболее вероятно.Вероятность изготовления прибора повышенного качества равна 0,74. Найти наивероятнейшее число приборов повышенного качества в партии из 80 приборов и вероятность этого результата. Вероятность изготовления стандартной детали равна 0,9. Какова вероятность того, что среди 200 деталей окажется 20 бракованных? Произведено 1000 независимых испытаний, вероятность появления события в одном испытании равна 0,7. Оценить вероятность того, что отклонение относительной частоты появления события от вероятности 0,7 по абсолютной величине не превзойдет 0,1. Определить надежность схемы, если Pi – отказ i – го элемента 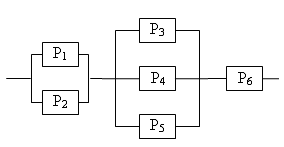 Вариант №22 Два игрока бросают монету по два раза каждый. Выигравшим считается тот, кто получит больше гербов. Найти вероятность того, что выигрывает первый игрок. Какова вероятность, что наудачу взятое трехзначное число будет четным? В прямоугольник с вершинами (-2; -1), (2; -1), (2; 1), (-2; 1) случайно брошена точка .Какова вероятность того, что она окажется внутри эллипса  ?В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчины? В ящике лежат 11 одинаковых по форме пуговицы, из них: 5 черных пуговиц. Работнице требуется пришить к очередному пальто 4 черные пуговицы. Определить вероятность того, что среди наугад взятых 4 пуговиц все пуговицы черные. Покупатель приобрел пылесос и полотер. Вероятность того, что пылесос не выйдет из строя в течение гарантийного срока, равна 0,95, для полотера такая вероятность равна 0,9. Найти вероятность того, что а) оба прибора выдержат гарантийный срок; б) хотя бы один выдержит гарантийный срок. Вероятность успешной попытки выполнить упражнение для каждого из двух спортсменов равна 0,5. Спортсмены упражнение выполняют по очереди, причем каждый делает по две попытки. Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами. На двух станках обрабатываются однотипные детали. Вероятность брака для станка №1 равна 0,03, а для станка №2 – 0,02. Обработанные детали складываются в одном месте; причем деталей со станка №1 складывается вдвое больше, чем со станка №2. Вычислить вероятность того, что взятая наудачу деталь не будет бракованной. В пирамиде установлено 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него? Найти наиболее вероятное число попаданий в мишень при 210 выстрелах и вероятность такого результата, если вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,7. Всхожесть семян некоторого растения равна 0,9. Какова вероятность того, что из 100 посеянных семян взойдет не менее 80. Вероятность наступления события в одном опыте равна 0,6. Вычислить вероятность того, при 6000 испытаниях событие произойдет не менее 340 и не более 380 раз. Определить надежность схемы, если Pi – надежность i – го элемента 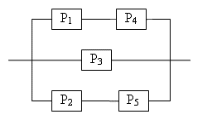 |