Реферат. Основные элементарные функции, их свойства и графики. Федеральное государственное бюджетное учреждение

• Название: Федеральное государственное бюджетное учреждение
• Дата: 21.12.2021
• Размер: 430.91 Kb.
• Имя файла: Реферат. Основные элементарные функции, их свойства и графики.docx
• Тип: Реферат; #311599

Министерство науки и высшего образования Российской Федерации

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ «Ивановский государственный химико-

технологический университет»

(ИГХТУ)

Факультет техники, управления и цифровой инфраструктуры

Кафедра высшей и прикладной математики
РЕФЕРАТ

Основные элементарные функции, их свойства и графики

Выполнила

Студентка группы 1/21

Шевцова Анна Александровна

Приняла:

ст.преподаватель

Бумагина Алла Николаевна
Реферат принят «__» _______ 2021 г.

Оценка: ______________________________

Иваново, 2021

Раздел 1. Постоянная функция.
Постоянная функция задается на множестве всех действительных чисел формулой y=C, где С-действительное число. График константы – это прямая, которая параллельна оси абсцисс и проходит через точку, имеющую координаты:(0, С).



Свойства постоянных функций:

• 
  область определения – все множество действительных чисел;
  
• 
  постоянная функция – четная;
  
• 
  область значений – множество, составленное из единственного числа C;
  
• 
  постоянная функция является невозрастающей и неубывающей;
  
• 
  постоянная функция – прямая линия, о выпуклости или вогнутости здесь речи быть не может;
  
• 
  асимптоты отсутствуют;
  
• 
  точка прохождения функции на координатной плоскости – ( 0 ; С)
  
  
  

График: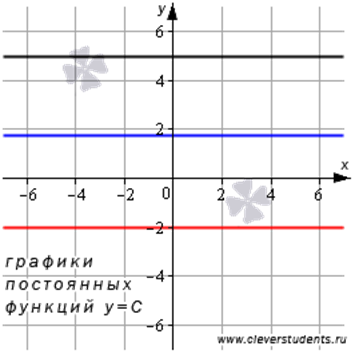










Раздел 2. Степенная функция.

Степенная функция задается формулой вида y=x^a.

Рассмотрим свойства и графики степенной функции для:

a=1; a=2; a=3; a=1/2; a=-1

1. 
   a=1, то есть у=х
   

Свойства:

• 
  область определения: x ∈ (− ∞; + ∞);
  
• 
  область значений: y ∈ (− ∞; + ∞);
  
• 
  функция является нечетной;
  
• 
  функция является возрастающей при x ∈ (− ∞; + ∞);
  
• 
  функция не имеет выпуклости;
  
• 
  точка перегиба отсутствует;
  
• 
  асимптоты отсутствуют;
  
  
  

График: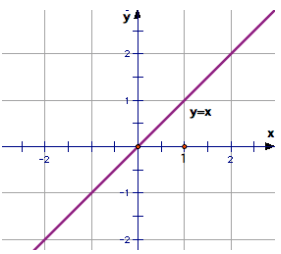

2. 
   a=2, то есть у=х²
   

Свойства:

• 
  область определения: x ∈ (− ∞; + ∞);
  
• 
  область значений: y ∈ [0; + ∞);
  
• 
  функция является четной;
  
• 
  функция является возрастающей при x ∈ [0; + ∞) и убывающей при x ∈ (− ∞; 0]
  
• 
  функция имеет вогнутость при x ∈ (− ∞; + ∞);
  
• 
  точки перегиба отсутствуют;
  
• 
  асимптоты отсутствуют.
  

График: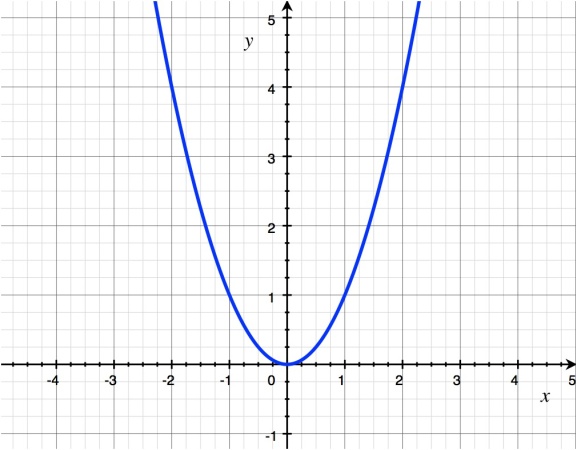

3. 
   а=3, то есть у=х³
   

Свойства:

• 
  область определения: x ∈ (− ∞; + ∞);
  
• 
  область значений: y ∈ (− ∞; + ∞);
  
• 
  функция является нечетной;
  
• 
  функция является возрастающей при x ∈ (− ∞; + ∞);
  
• 
  функция имеет выпуклость при x ∈ (− ∞; 0] и вогнутость при
  

x ∈ [0; + ∞);

• 
  точка перегиба имеет координаты (0; 0);
  
• 
  асимптоты отсутствуют
  
  
  

График: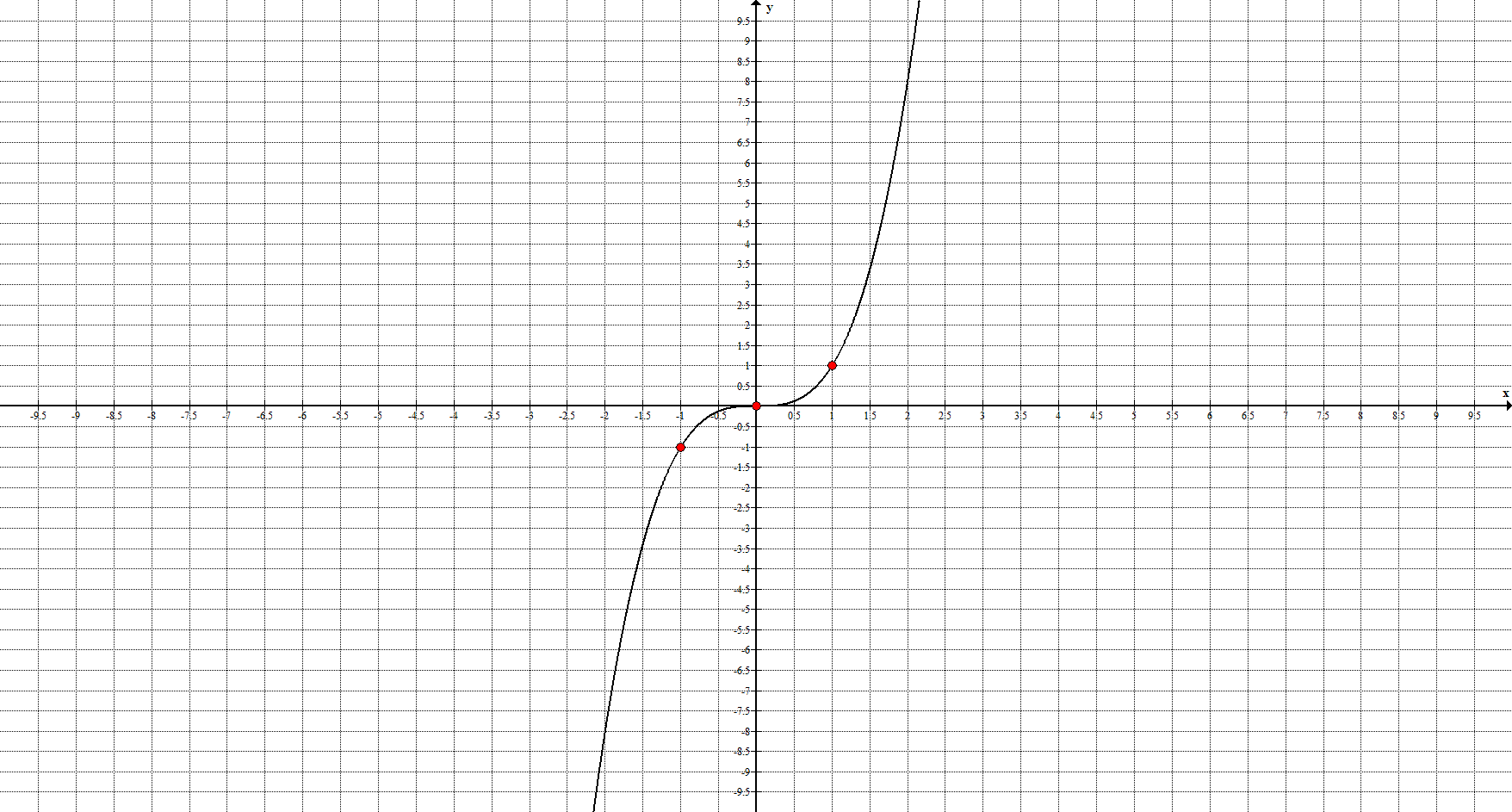

4. 
   а=1/2, то есть у=х^1\2 или у=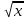
   

Свойства:

• 
  область определения: x ∈ [0; + ∞);
  
• 
  область значений: y ∈ [0; + ∞);
  
• 
  данная функция – функция общего вида (не является ни нечетной, ни четной);
  
• 
  функция является возрастающей при x ∈ [0; + ∞);
  
• 
  функция имеет выпуклость при x ∈ (0; + ∞);
  
• 
  точки перегиба отсутствуют;
  
• 
  асимптоты отсутствуют;
  

График: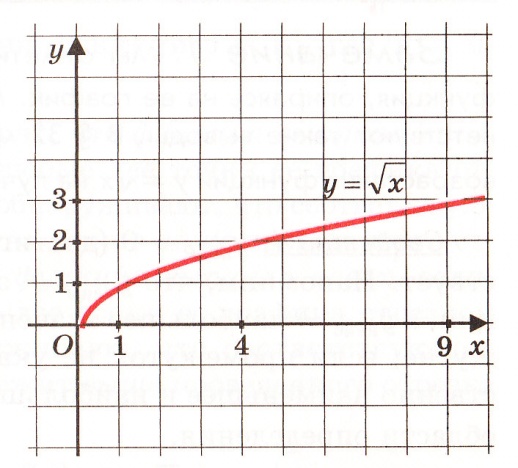

5. 
   а=-1, то есть у=х^-1 или у=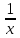
   

Свойства:

• 
  область определения: x ∈ (− ∞; 0) ∪ (0; + ∞)
  
• 
  область значений: y ∈ (− ∞; 0) ∪ (0; + ∞);
  
• 
  функция является нечетной;
  
• 
  функция является убывающей при x ∈ (− ∞; 0) ∪ (0; + ∞);
  
• 
  функция имеет выпуклость при x ∈ (− ∞; 0) и вогнутость при
  

x ∈ (0; + ∞);

• 
  точки перегиба отсутствуют;
  
• 
  горизонтальная асимптота – прямая y = 0
  

График: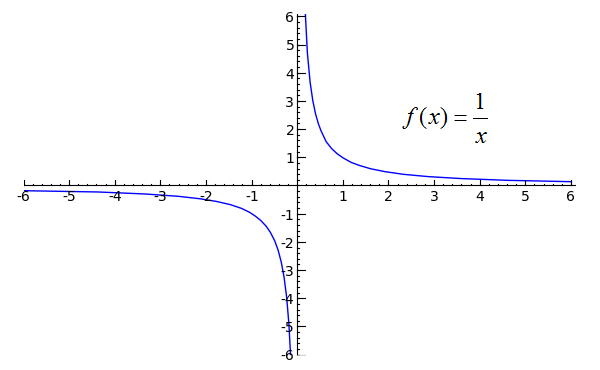


Раздел 3. Показательная функция.

Показательная функция имеет вид y = a^х, где а> 0 и а ≠1

Рассмотрим свойства и графики функций для:

01; y=e^x

1. 
   0
   

Свойства:

• 
  область определения – все множество действительных чисел; область значений: y ∈ (0; + ∞);
  
• 
  данная функция – функция общего вида (не является ни нечетной, ни четной);
  
• 
  показательная функция, у которой основание меньше единицы, является убывающей на всей области определения;
  
• 
  функция имеет вогнутость при x ∈ (− ∞; + ∞);
  
• 
  точки перегиба отсутствуют;
  
• 
  горизонтальная асимптота – прямая y = 0 при переменной x, стремящейся к + ∞
  

График: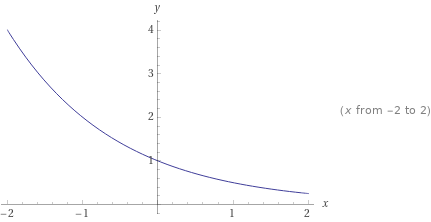

2. 
   a>1
   

Свойства:

• 
  область определения – все множество действительных чисел;
  
• 
  область значений: y ∈ (0; + ∞);
  
• 
  данная функция – функция общего вида (не является ни нечетной, ни четной);
  
• 
  показательная функция, у которой основание больше единицы, является возрастающей при x ∈ (− ∞; + ∞);
  
• 
  функция имеет вогнутость при x ∈ (− ∞; + ∞);
  
• 
  точки перегиба отсутствуют;
  
• 
  горизонтальная асимптота – прямая y = 0 при переменной x, стремящейся к − ∞;
  

График: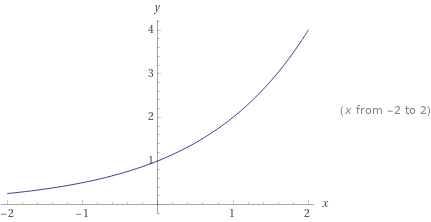




3) у=е^х

Свойства:

• 
  область определения – все множество действительных чисел;
  
• 
  область значений: y ∈ (0; + ∞);
  
• 
  данная функция – функция общего вида (не является ни нечетной, ни четной);
  
• 
  показательная функция, у которой основание больше единицы, является возрастающей при x ∈ (− ∞; + ∞);
  
• 
  функция имеет вогнутость при x ∈ (− ∞; + ∞);
  
• 
  точки перегиба отсутствуют;
  
• 
  горизонтальная асимптота – прямая y = 0 при переменной x, стремящейся к − ∞;
  
  
  

График: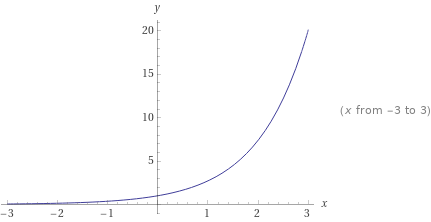




Раздел 4. Логарифмическая функция.

Логарифмическая функция имеет вид y = log_а(x), где a> 0, a ≠ 1

Рассмотрим свойства и графики функций для:

01; y=lg(x); y=ln(x)

1. 
   0
   

Свойства:

• 
  область определения: x ∈ (0; + ∞).  Когда х стремится к нулю справа, значения функции стремятся к +∞;
  
• 
  область значений: y ∈ (− ∞; + ∞);
  
• 
  данная функция – функция общего вида (не является ни нечетной, ни четной); логарифмическая функция является убывающей на всей области определения;
  
• 
  функция имеет вогнутость при x ∈ (0; + ∞);
  
• 
  точки перегиба отсутствуют;
  
• 
  асимптоты отсутствуют;
  

График:

2. 
   a>1
   

Свойства:

• 
  область определения: x ∈ (0; + ∞).  Когда х стремится к нулю справа, значения функции стремятся к -∞;
  
• 
  область значений: y ∈ (− ∞; + ∞) (все множество действительных чисел);
  
• 
  данная функция – функция общего вида (не является ни нечетной, ни четной);
  
• 
  логарифмическая функция является возрастающей при x ∈ (0; + ∞);
  
• 
  функция имеет выпуклость при x ∈ (0; + ∞);
  
• 
  точки перегиба отсутствуют;
  
• 
  асимптоты отсутствуют;
  

График: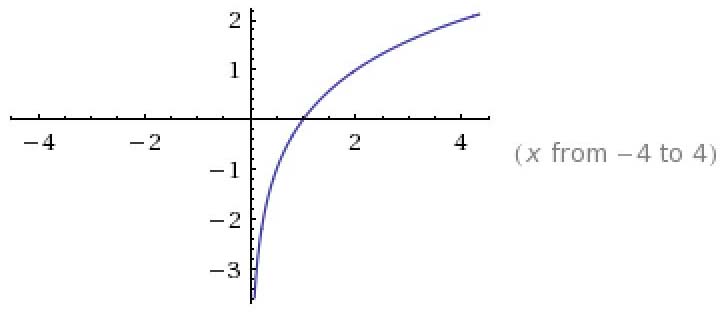

3. 
   у=lg(x)
   

Свойства:

• 
  область определения: x ∈ (0; + ∞).  Когда х стремится к нулю справа, значения функции стремятся к -∞;
  
• 
  область значений: y ∈ (− ∞; + ∞) (все множество действительных чисел);
  
• 
  данная функция – функция общего вида (не является ни нечетной, ни четной);
  
• 
  логарифмическая функция является возрастающей при x ∈ (0; + ∞);
  
• 
  функция имеет выпуклость при x ∈ (0 ; + ∞) ;
  
• 
  точки перегиба отсутствуют;
  
• 
  асимптоты отсутствуют;
  

График: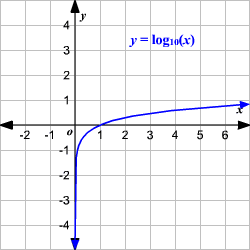

4. 
   у=ln(x)
   

Cвойства: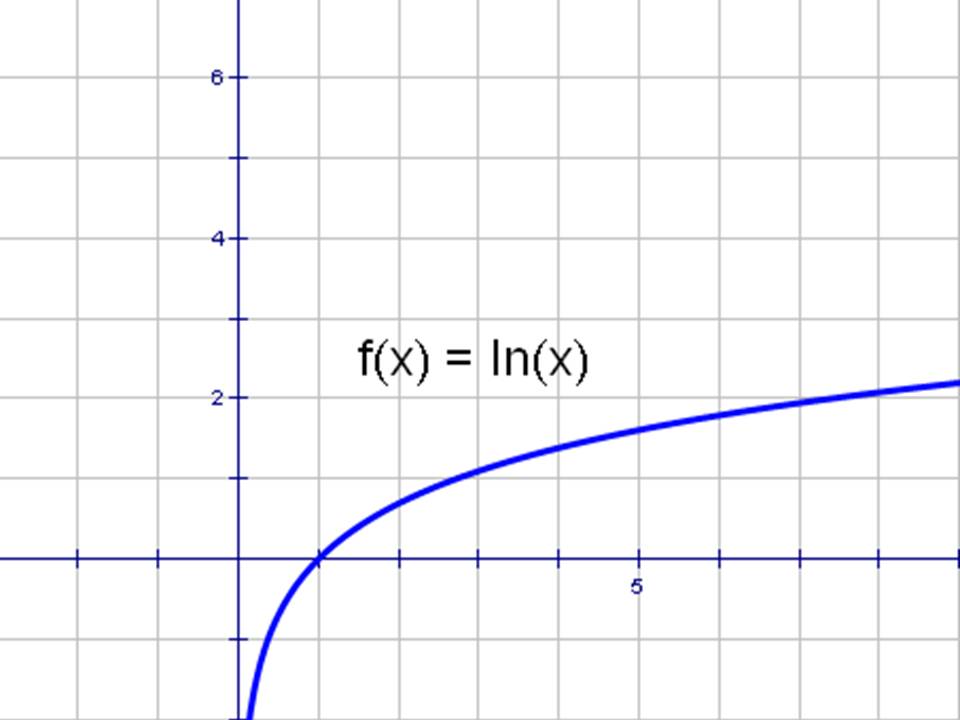

Аналогичны y=lg(x)



График:


Раздел 5. Тригонометрические функции

Тригонометрические функции – это синус, косинус, тангенс и котангенс.

1. 
   Функция синус: y = sin (х)
   

Свойства:

• 
  область определения: все множество действительных чисел
  

x ∈ (− ∞; + ∞);

• 
  наименьший положительный период: Т = 2 π;
  
• 
  функция обращается в нуль, когда x = π ⋅ k, где k ∈ Z (Z – множество целых чисел);
  
• 
  область значений: y ∈ (− 1; 1];
  
• 
  данная функция – нечетная;
  
• 
  функция является возрастающей при x ∈ (− π/2 + 2 π ⋅ k; π/2 + 2 π ⋅ k],
  k ∈Z  и убывающей при x ∈ ( π/2 + 2 π ⋅ k ;3π/2 + 2 π ⋅ k ] , k ∈Z;
  
• 
  функция синус имеет локальные максимумы в точках (π/2 + 2 π ⋅ k; 1),
  k ∈ Z и локальные минимумы в точках ( − π/2 + 2 π ⋅ k ;   − 1 ) ,   k ∈ Z;
  
• 
  функция синус вогнутая, когда x ∈ (− π + 2 π ⋅ k; 2 π ⋅ k], k ∈ Z и выпуклая, когда x ∈ (2 π ⋅ k; π + 2 π ⋅ k], k ∈ Z;
  
• 
  точки перегиба имеют координаты (π ⋅ k; 0), k ∈ Z;
  
• 
  асимптоты отсутствуют.
  

График: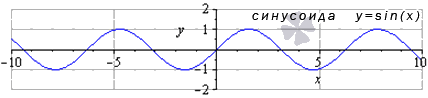

2. 
   Функция косинус y = cos (х)
   

• 
  Свойства:
  область определения:  x ∈ ( − ∞ ;   + ∞ );
  
• 
  наименьший положительный период: Т = 2 π;
  
• 
  функция обращается в нуль, когда x = π/2 + π ⋅ k при k ∈ Z
  (Z – множество целых чисел);
  
• 
  область значений: y ∈ (− 1; 1];
  
• 
  данная функция – четная;
  
• 
  функция является возрастающей при x ∈ (− π + 2 π ⋅ k; 2 π ⋅ k],
  k ∈ Z и убывающей при x ∈ (2 π ⋅ k; π + 2 π ⋅ k], k ∈ Z;
  
• 
  функция косинус имеет локальные максимумы в точках (2 π ⋅ k; 1),  
  k ∈ Z и локальные минимумы в точках (π + 2 π ⋅ k; − 1), k ∈ z;
  
• 
  функция косинус вогнутая, когда x ∈ (π/2 + 2 π ⋅ k; 3π/2 + 2 π ⋅ k],
  

  k ∈ Z и выпуклая, когда x ∈ (– π/2 + 2 π ⋅ k; π/2 + 2 π ⋅ k], k ∈ Z;

• 
  точки перегиба имеют координаты (π/2 + π ⋅ k; 0), k ∈ Z;
  
• 
  асимптоты отсутствуют.
  

График: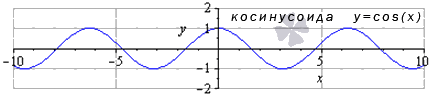

3. 
   Функция тангенс y = tg (х)
   

Свойства:

• 
  область определения: x ∈ (− π/2 + π ⋅ k; π/2 + π ⋅ k)  
  ( Z – множество целых чисел);
  
• 
  Поведение функции тангенс на границе области определения 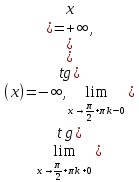. Таким образом, прямые x = π/2 + π ⋅ k (k ∈ Z) – вертикальные асимптоты;
  
• 
  наименьший положительный период: Т = π;
  
• 
  функция обращается в нуль, когда x = π ⋅ k при k ∈ Z
  (Z – множество целых чисел);
  
• 
  область значений: y ∈ (− ∞; + ∞);
  
• 
  данная функция – нечетная;
  
• 
  функция является возрастающей при (− π/2 + π ⋅ k; π/2 + π ⋅ k), k ∈ Z;
  
• 
  функция тангенс является вогнутой при x ∈ [π ⋅ k; π 2 + π ⋅ k),
  k ∈ Z  и выпуклой при x ∈ (− π/2 + π ⋅ k; π ⋅ k], k ∈ Z;
  
• 
  точки перегиба имеют координаты (π ⋅ k; 0), k ∈ Z;
  
• 
  наклонные и горизонтальные асимптоты отсутствуют.
  

График: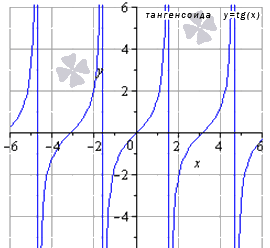

4. 
   Функция котангенс: y = ctg(х)
   

Свойства:

• 
  область определения: x ∈ (π ⋅ k; π + π ⋅ k), где k ∈ Z
  ( Z – множество целых чисел);
  
• 
  Поведение функции котангенс на границе области определения .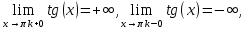
  Таким образом, прямые x = π ⋅ k (k ∈ Z) – вертикальные асимптоты;
  
• 
  наименьший положительный период: Т = π;
  
• 
  функция обращается в нуль, когда x = π/2 + π ⋅ k при k ∈ Z 
  (Z – множество целых чисел);
  
• 
  область значений: y ∈ (− ∞; + ∞);
  
• 
  данная функция – нечетная;
  
• 
  функция является убывающей при x ∈ (π ⋅ k; π + π ⋅ k), k ∈ Z;
  
• 
  функция котангенс является вогнутой при x ∈ (π ⋅ k; π 2 + π ⋅ k], k ∈ Z и выпуклой при x ∈ [− π/2 + π ⋅ k; π ⋅ k), k ∈ Z;
  
• 
  точки перегиба имеют координаты (π/2 + π ⋅ k; 0), k ∈ Z;
  
• 
  наклонные и горизонтальные асимптоты отсутствуют.
  

График: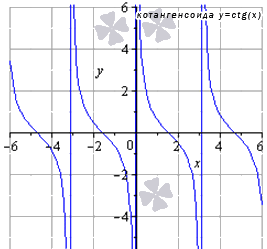







Раздел 6. Обратные тригонометрические функции.

Обратные тригонометрические функции – это арксинус, арккосинус, арктангенс и арккотангенс
В данной работе рассмотрим только арксинус и арккосинус.

1. 
   Функция арксинус: y = arcsin (х)
   

Свойства:

• 
  область определения: x ∈ (− 1; 1];
  
• 
  область значений: y ∈ (− π/2; π/2];
  
• 
  данная функция – нечетная;
  
• 
  функция является возрастающей на всей области определения;
  
• 
  функция арксинус имеет вогнутость при x ∈ (0; 1] и выпуклость при x ∈ (− 1; 0];
  
• 
  точки перегиба имеют координаты (0; 0), она же – нуль функции;
  
• 
  асимптоты отсутствуют.
  

Графики: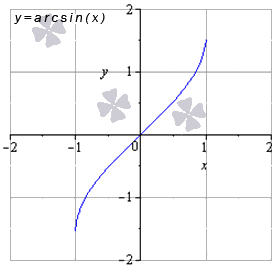

2. 
   Функция арккосинус: y=arccos(x)
   

Свойства:

• 
  область определения: x ∈ (−1; 1];
  
• 
  область значений: y ∈ (0; π];
  
• 
  данная функция - общего вида (ни четная, ни нечетная);
  
• 
  функция является убывающей на всей области определения;
  
• 
  функция арккосинус имеет вогнутость при x ∈ (−1; 0]
  и выпуклость при x ∈ (0; 1];
  
• 
  точки перегиба имеют координаты (0; π/2);
  
• 
  асимптоты отсутствуют.
  

График: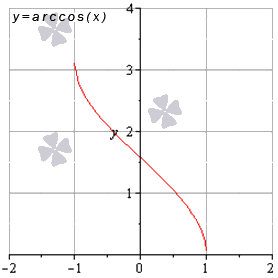