методические указания гидравлика и гидропневмопривод. Федеральное государственное образовательное учреждение высшего профессионального образования

• Название: Федеральное государственное образовательное учреждение высшего профессионального образования
• Дата: 10.01.2019
• Размер: 0.95 Mb.
• Имя файла: методические указания гидравлика и гидропневмопривод.doc
• Тип: Контрольная работа; #63171
• страница: 3 из 5

Глава 3. Истечение жидкости через отверстия и насадки
В процессе истечения жидкости происходит преобразование потенциальной энергии жидкости в кинетическую.

Из уравнения Бернулли легко выводится выражение для скорости истечения:
, (3.1)
где Н - расчетный напор, который в общем случае равен сумме геометрического и пьезометрического напоров, т. е.
, (3.2)
φ - коэффициент скорости, определяемый как
. (3.3)
здесь α - коэффициент Кориолиса, в приближенных расчетах обычно принимают α = 1;

ζ - коэффициент местного сопротивления.

Расход жидкости при истечении через отверстия, насадки, дроссели и клапаны определяется произведением скорости истечения на площадь сечения струи. Однако последняя часть бывает меньше площади отверстия вследствие сжатия струи. Поэтому вводится коэффициент сжатия

, (3.4)
где S_с и S_отв - площади сечения струи и отверстия.

Отсюда расход равен
(3.5)
Вместо расчетного напора Н_расч часто используется расчетный перепад давления р_расч = Н_расч · ρ · g и вместо (3.5) пишут:
(3.6)
Истечение жидкости может происходить либо в газовую среду, например, в атмосферный воздух, либо в среду той же жидкости. В последнем случае вся кинетическая энергия струи теряется на вихреобразования.

Отверстием в тонкой стенке называется отверстие, диаметр которого d_отв больше толщины стенки . В этом случае коэффициент расхода μ и другие коэффициенты однозначно определяются числом Рейнольдса, а в приближенных расчетах обычно принимают: ε = 0,64; φ = 0,97; α = 1; ζ = 0,065; μ = 0,62.

Внешний цилиндрический насадок представляет собой короткую трубу, приставленную к отверстию снаружи, или отверстие, диаметр которого d_отв в 2...6 раз меньше толщины стенки . Коэффициенты в приближенных расчетах обычно принимают μ = φ = 0,82; ε = 1.

Внутренний цилиндрический насадок - это короткая трубка, приставленная к отверстию изнутри. Для него можно принимать μ = φ = 0,71; ε = 1.

Сопло, или коноидальный насадок, обеспечивает плавное, безотрывное сужение потока внутри насадка и параллельноструйное течение на выходе. Для сопла в расчетах можно принимать: μ = φ = 0,97; ε=1.

Указания к решению задач

Задачи данного раздела можно решать без записи уравнения Бернулли. Так, если дана задача на истечение через отверстие, насадок или дроссель (жиклер) и задан коэффициент расхода, то следует применить основное выражение (3.5). При этом следует помнить, что расчетный напор в общем случае складывается из разностей геометрических и пьезометрических высот (3.2).

Следует знать, что коэффициент расхода μ однозначно определяется коэффициентами сжатия струи ε и скорости φ (или сопротивления ζ).

Указанное выше основное выражение для расхода справедливо и при истечении через отверстия, насадки и дроссели в среду, заполненную той же самой жидкостью (истечение под уровень). При этом кинетическая энергия, теряемая на вихреобразования, учитывается коэффициентом расхода.

Если истечение жидкости происходит при переменном напоре (опорожнение резервуаров), то в каждый данный момент движение жидкости можно рассматривать как установившееся.

Примеры решения задач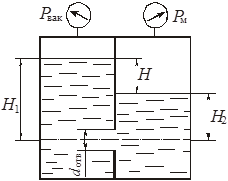





Пример 3.1. Определить направление истечения воды через отверстие диаметром d = 5 мм и расход, если разность уровней Н = 2 м, показание вакуумметра Р_вак соответствует 147 мм рт. ст., показание манометра Р_м = 0,25 МПа, коэффициент расхода μ = 0,62. Удельные веса ртути и воды принять γ_рт = 13,6 · 10⁴ Н/м³; γ = 10⁴ Н/м³.

Решение:

Для определения расхода воспользуемся формулой (3.5):

Расчетный напор определяется разностью полных напоров до отверстия и после него. Поскольку направление истечения нам неизвестно, допустим, что оно происходит слева направо (см. рис.). Обозначив абсолютные давления над жидкостью слева Р₁, справа Р₂, глубины погружения Н₁ и Н₂, для Н_расч получим (сравни с формулой 3.2)

Учитывая, что Р₁ = Р_атм - Р_вак; Р₂ = Р_атм + Р_м; Н₁ - Н₂ = Н;

получим

Поскольку в задаче вакуум задан высотой ртутного столба, выразим необходимое нам вакуумметрическое давление Р_вак как
Р_вак = γ_рт · h_рт,

и тогда окончательно для расчетного напора получим:

Так как Н_расч отрицательный, истечение будет происходить в направлении, противоположном принятому, т.е. справа налево.

Расход при этом определится как

ЗАДАЧИ К ГЛАВЕ 3

Задача 32. Определить расход жидкости (ρ= 800 кг/м³), вытекающей из бака через отверстие площадью S_отв = 1 см². Показание ртутного прибора, измеряющего давление воздуха, h = 268 мм, высота Н = 2 м, коэффициент расхода отверстия μ = 0,60.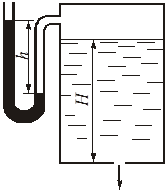




Задача 33. При исследовании истечения через круглое отверстие диаметром d_отв = 10 мм получено: диаметр сжатого сечения струи d_с = 8 мм; напор Н = 2 м; время наполнения объема W = 10 л; t = 16,8 с. Определить коэффициент сжатия ε, скорости φ, расхода μ и сопротивления ζ. Распределение скоростей по сечению струи принять равномерным.



Задача 34. При истечении жидкости через отверстие диаметром d_отв = 10 мм измерены: расстояние х = 5 м (см. рис.), высота у = 4 м, напор Н = 1,7 м и расход жидкости Q = 0,275 л/с. Подсчитать коэффициенты сжатия ε, скорости φ, расхода μ и сопротивления ζ. Распределение скоростей по сечению струи принять равномерным. Сопротивлением воздуха пренебречь.




Задача 35. «Сосуд Мариотта» представляет собой плотно закрытый сосуд, в крышке которого укреплена трубка, сообщающая сосуд с атмосферой. Трубка может быть укреплена на различной высоте. В стенке сосуда имеется отверстие диаметром d = 10 мм, через которое происходит истечение в атмосферу. Какое давление установится в сосуде на уровне нижнего обреза трубки при истечении? Определить скорость истечения и время опорожнения «сосуда Мариотта» от верха до нижнего обреза трубки. Объемом жидкости в трубке и сопротивлением при истечении пренебречь (ε = 1).

Форма сосуда цилиндрическая, D = 100 мм; Н = 2 м, h₁ = 0,2 м, h₂ = 1 м.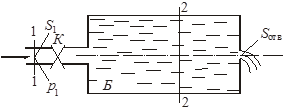




Задача 36. Вода под избыточным давлением р₁ = 0,3 МПа подается по трубе с площадью поперечного сечения S₁ = 5 см² к баллону Б, заполненному водой. На трубе перед баллоном установлен кран К с коэффициентом местного сопротивления ζ = 5. Из баллона Б вода вытекает в атмосферу через отверстие S_отв = 1 см²; коэффициент расхода отверстия равен μ = 0,63. Определить расход воды Q.

У к а з а н и е. Записать уравнение Бернулли для сечения 1-1 и 2-2 и основную формулу для расхода при истечении.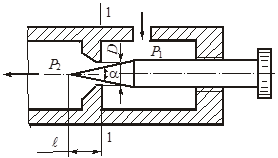




Задача 37. На рисунке изображена схема регулируемого игольчатого дросселя. Определить, на какое расстояние  необходимо вдвинуть иглу в дросселирующее отверстие для обеспечения перепада давления Δр = р₁ - р₂ = 3 МПа, если угол иглы α = 30^о, диаметр дросселирующего отверстия D = 6 мм, его коэффициент расхода μ = 0,8, расход жидкости Q = 1,2 л/с, плотность рабочей жидкости ρ = 900 кг/м³.

У к а з а н и е: площадь дросселирующего кольца определить по приближенной формуле S = S_о - S_и, где S_о - площадь отверстия, S_и - площадь иглы в сечении 1-1.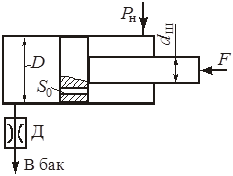



Задача 38. Жидкость с плотностью ρ = 850 кг/м³ подается от насоса в гидроцилиндр, а затем через отверстие в поршне площадью S_о = 5 мм² и гидродроссель Д в открытый бак.

) Определить, при какой площади проходного сечения дросселя Д поршень будет находиться в неподвижном равновесии под действием силы F = 3000 Н, если диаметр поршня D = 100 мм, диаметр штока d_ш = 80 мм, коэффициент расхода отверстия в поршне μ_о = 0,8, коэффициент расхода дросселя μ_др = 0,65, избыточное давление, создаваемое насосом р_н = 1 МПа.

) Определить площадь проходного сечения дросселя Д, при которой поршень будет равномерно перемещаться со скоростью υ_п = 1 см/с вправо.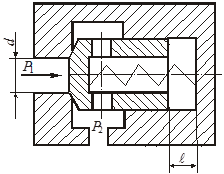




Задача 39. Обратный клапан диаметром d = 20 мм служит для пропуска жидкости (ρ = 900 кг/м³) только в одном направлении. Определить перепад давления Δр = р₁ - р₂ на клапане, если р₁ = 1,6 МПа. Жесткость пружины с = 13 Н/мм, ее предварительное поджатие у_о = 8 мм, максимальный ход клапана  = 3 мм, коэффициент расхода μ = 0,8, объемный расход Q = 1 л/с.

Задача 40. Считая жидкость несжимаемой, определить скорость движения поршня под действием силы F = 10 кН на штоке, диаметр поршня D = 80 мм, диаметр штока d = 30 мм, проходное сечение дросселя S_др = 2 мм², его коэффициент расхода μ = 0,75, избыточное давление слива р_с = 0, плотность рабочей жидкости ρ = 900 кг/м³.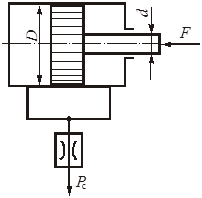




Задача 41. Определить время для вытекания всей воды из цилиндрического бака, если его диаметр D = 0,8 м, наполнение равно h = 0,7 м. Диаметр трубы d = 70 мм, длина  = 0,8 м. Температура жидкости 20 ^оС. Чему равно отношение продолжительности вытекания первой и второй половины объема жидкости?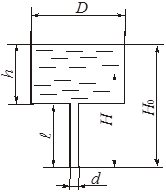




Указание: Продолжительность истечения от уровня Н_о до уровня Н может быть определена по формуле: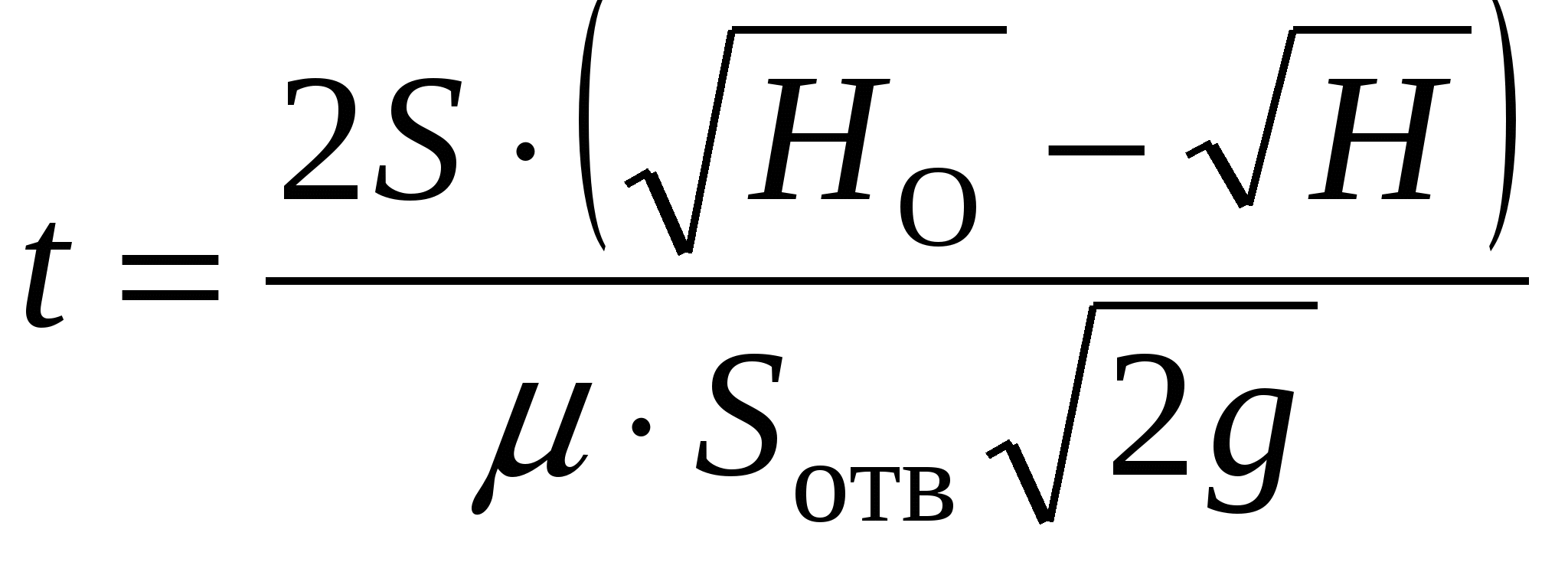

,
где S - площадь сечения сосуда;

Н_о - начальный напор, с которого начинается опорожнение сосуда;

Н - конечный напор, до которого опорожняется сосуд;

μ - коэффициент расхода, который может быть определен по формуле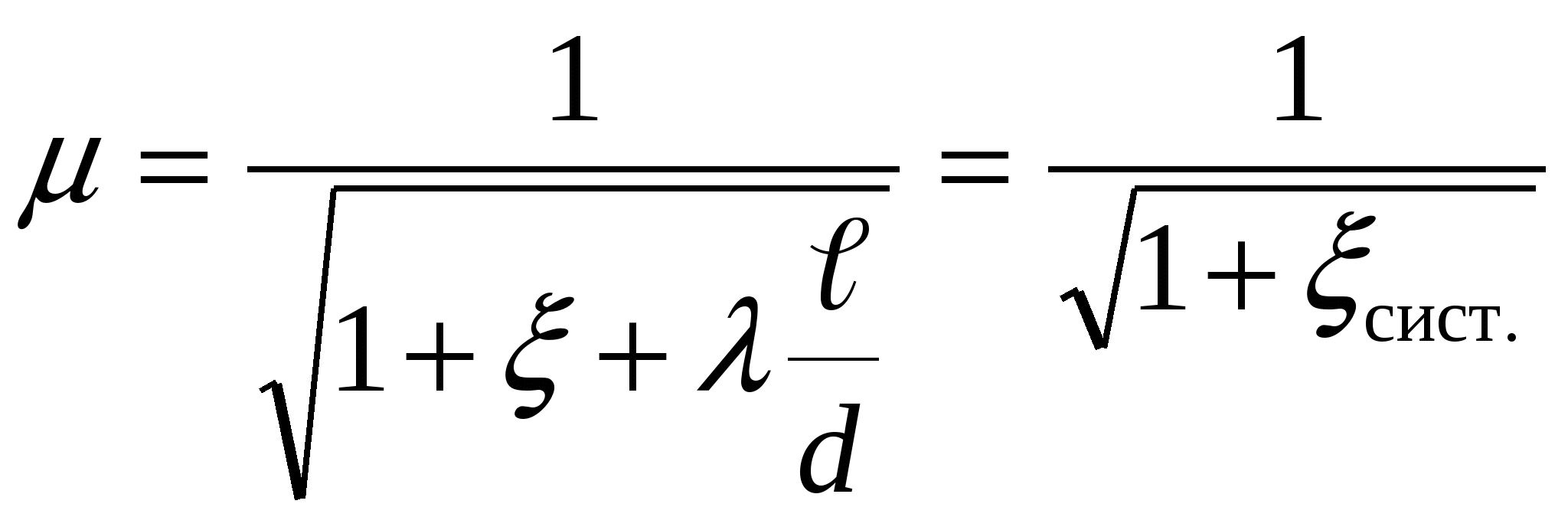
,
где ξ_сист. - суммарный коэффициент сопротивления.
Глава 4. Гидромашины
Понятие «гидромашины» включает в себя насосы и гидродвигатели. В насосе происходит преобразование энергии двигателя (как правило, электродвигателя) в энергию потока жидкости, а гидродвигатель преобразует энергию потока жидкости в механическую работу.

По принципу действия гидромашины делят на объемные и динамические.

Объемными называют гидромашины, рабочий процесс которых основан на попеременном заполнении рабочих камер жидкостью и вытеснением ее из этих камер. Рабочей камерой объемной гидромашины называют ограниченное пространство внутри машины, периодически изменяющее свой объем и попеременно сообщающееся с входом и выходом.

В объемных насосах перемещение жидкости осуществляется путем вытеснения ее из рабочих камер вытеснителями, которые совершают поступательное (поршневые насосы), вращательное или сложное вращательно-поступательное движение (роторные насосы).

В динамических гидромашинах жидкость в камере находится под силовым воздействием и имеет постоянное сообщение со входным и выходным патрубками.

Основной разновидностью динамических насосов являются лопастные и, в частности, центробежные насосы. В центробежном насосе передача мощности от двигателя к жидкости происходит в процессе движения ее по межлопаточным каналам быстро вращающегося рабочего колеса из центральной его части к периферии.

Напор Н, развиваемый центробежным насосом, зависит от его подачи (расхода) Q. Зависит от расхода также η - к.п.д. насоса, N - полезная мощность, - допустимая вакуумметрическая высота. Эти зависимости называются характеристиками насоса.

Обычно пользуются экспериментальными кривыми Н_н = f (Q), которые имеют вид плавно спадающих кривых. Кривая зависимости к.п.д. насоса от подачи Q выходит из начала координат (при Q = 0), достигает максимума при некоторой оптимальной подаче.

Для двух геометрически подобных центробежных насосов и для подобных режимов их работы справедливы следующие соотношения: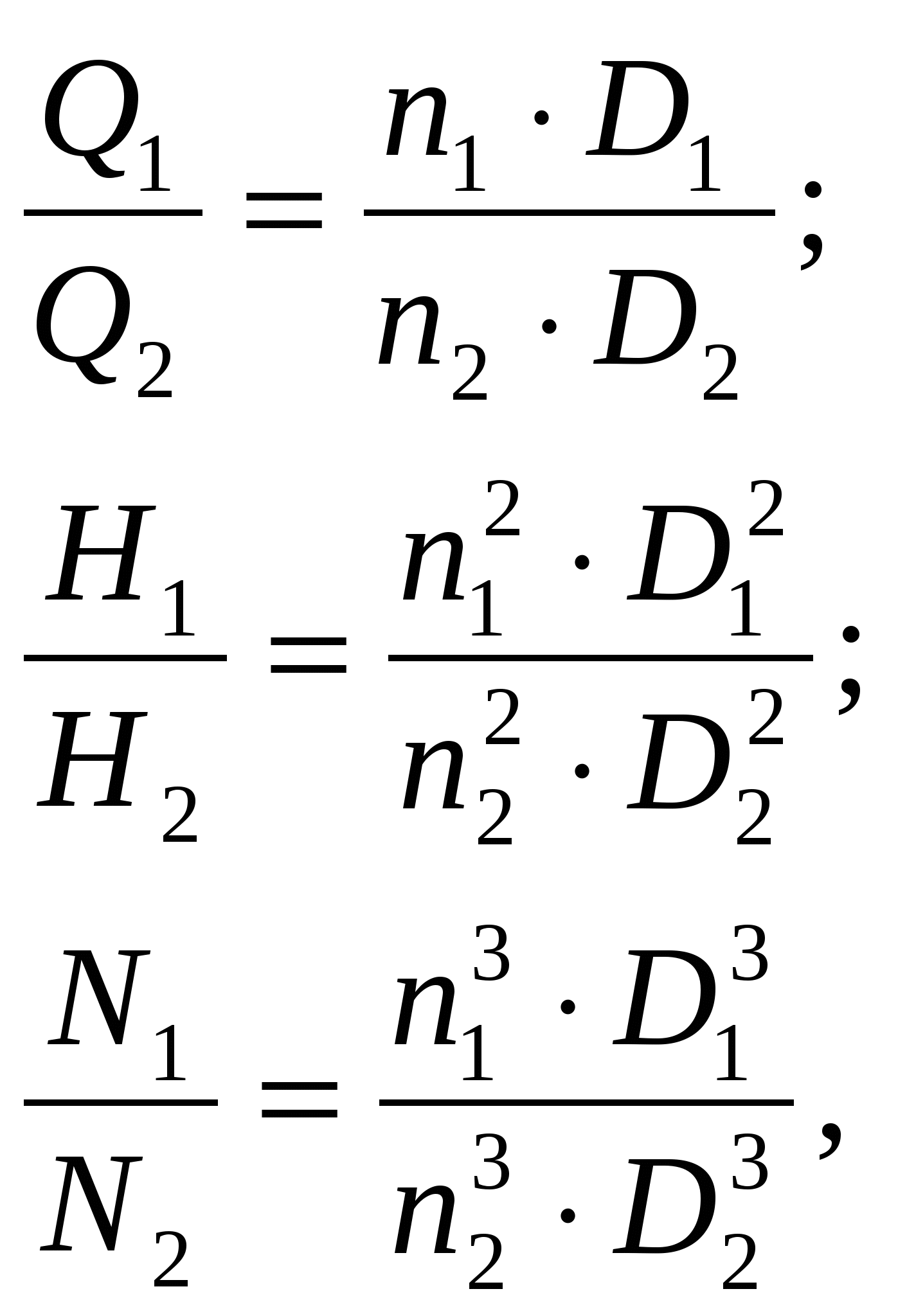
(4.1)
где D - диаметры рабочих колес.

Приведенные формулы позволяют производить пересчет характеристик центробежных насосов с одной частоты n₁ и диаметра D₁ на другую частоту n₂ и другой диаметр D₂. Для одного итого же насоса D₁ = D₂ и формулы упрощаются.

Гидравлический и объемный к.п.д. насоса при сохранении подобия режимов его работы остаются приблизительно постоянными в силу автомодельности. Полный к.п.д. насоса при этом в первом приближении можно считать также постоянным.

Когда абсолютное давление на входе в центробежный насос оказывается слишком низким, на входных элементах лопаток рабочего колеса возникает кавитация. При этом напор, создаваемый насосом, и его к.п.д. резко падают.

Кавитационным запасом называют разность между полным напором жидкости во входном патрубке насоса и давлением насыщенных паров жидкости, т. е.
, (4.2)
где р_в и v_в, - давление и скорость во входном патрубке насоса;

р_н.п - давление насыщенных паров жидкости при данной температуре.

Значение кавитационного запаса, при котором начинается кавитация в насосе, называют критическим или минимально допустимым кавитационным запасом и обозначают . Эта величина будет тем больше, чем больше подача насоса и частота вращения его колеса, и может быть найдена по следующей формуле С. С. Руднева:
, (4.3)

где С = 800...1000 - коэффициент для обычных насосов. Для насосов с повышенными кавитационными свойствами С ≤ 1300. Это значение соответствует при подстановке в формулу (5.10) (м); n (об/мин); Q (м³/с).

Формула С. С. Руднева позволяет находить минимально допустимое абсолютное давление p_{в min} перед входом в насос при заданных Q и n, или Q_max при заданных p_в и n, или n_max при заданных р_в и Q.

С явлением кавитации связано и ограничение на высоту положения насоса относительно уровня жидкости в исходном резервуаре. Допустимая высота всасывания определяется также с использованием формулы Руднева:
,
где - потери во всасывающем трубопроводе; φ = 1,1 ÷ 1,2.

Указания к решению задач

Задачи данной главы сводятся к определению мощности, потребляемой насосом, подачи насоса, построению характеристик центробежных насосов при различной частоте вращения. Для их решения необходимо использовать формулы и соотношения (4.1)...(4.3), а также известные формулы для определения геометрических размеров.

Примеры решения задач