методические указания гидравлика и гидропневмопривод. Федеральное государственное образовательное учреждение высшего профессионального образования

• Название: Федеральное государственное образовательное учреждение высшего профессионального образования
• Дата: 10.01.2019
• Размер: 0.95 Mb.
• Имя файла: методические указания гидравлика и гидропневмопривод.doc
• Тип: Контрольная работа; #63171
• страница: 2 из 5

Глава 2. Применение уравнения Бернулли. Гидравлические сопротивления
При решении некоторых простейших задач о движении жидкостей часто в первом приближении делают допущение о том, что движущаяся жидкость является идеальной. Под идеальной понимают жидкость абсолютно несжимаемую и нерасширяемую, не способную сопротивляться растяжению и сдвигу, а также лишенную свойства испаряемости (р_н.п = 0). Главное, чем отличается жидкость идеальная от жидкости реальной, - это отсутствие у нее вязкости, вызывающей способность сопротивления сдвигу, т. е. возникновению касательных напряжений (трения в жидкости).

Следовательно, в движущейся идеальной жидкости возможен лишь один вид напряжений - напряжение сжатия, т. е. давление р, а касательное напряжение τ = 0.

Основными уравнениями, позволяющими решать простейшие задачи о движении идеальной жидкости, является уравнение расхода и уравнение Бернулли.

Уравнение расхода представляет собой условие неразрывности (сплошности) потока несжимаемой жидкости, или, что то же самое, равенство объемных расходов в каких-то двух поперечных сечениях одного и того же потока, например 1 и 2, т. е. Q₁ = Q₂ или v₁S₁ = v₂S₂. Отсюда следует, что
, (2.1)
т. е. скорости обратно пропорциональны площадям поперечных сечений потоков. При этом предполагается, что скорость во всех точках данного сечения одинакова.

Уравнение Бернулли для потока идеальной жидкости выражает собой закон сохранения удельной энергии жидкости вдоль потока. Под удельной понимают энергию, отнесенную к единице веса, объема или массы жидкости. Обычно удобнее бывает относить энергию к единице веса. В этом случае уравнение Бернулли, записанное для сечений 1 и 2 элементарной струйки или потока идеальной жидкости, имеет вид
, (2.2)
где z - вертикальные координаты центров тяжести сечений или удельная энергия положения;

р/(ρg) - пьезометрическая (приведенная пьезометрическая) высота, или удельная энергия давления; ²/(2g) - скоростной напор, или удельная кинетическая энергия; Н - полный напор, или полная удельная энергия жидкости.

Для потока реальной (вязкой) жидкости уравнение Бернулли следует писать в таком виде:
, (2.3)
где v_ср - средняя по сечению скорость, равная v_ср = Q/S;

α - коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечениям и равный отношению действительной кинетической энергии потока к кинетической энергии того же потока, но при равномерном распределении скоростей;

Σh - суммарная потеря полного напора между сечениями 1 и 2, обусловленная вязкостью жидкости.

Различают два вида гидравлических потерь напора: местные потери и потери на трение по длине.

Местные потери напора происходят в так называемых местных гидравлических сопротивлениях, т. е. в местах изменения формы и размеров русла, где поток так или иначе деформируется - расширяется, сужается, искривляется - или имеет место более сложная деформация. Местные потери выражают формулой Вейсбаха
, (2.4)
где v - средняя скорость потока в сечении перед местным сопротивлением (при расширении) или за ним (при сужении) и в тех случаях, когда рассматривают потери напора в гидроарматуре различного назначения;

ζ_м - безразмерный коэффициент местного сопротивления.

Числовое значение коэффициента в основном определяется формой местного сопротивления, его геометрическими параметрами, но иногда влияет также число Рейнольдса, которое для труб диаметром d выражается формулой
, (2.5)
здесь  - кинематическая вязкость жидкости, выражаемая в м²/с или см²/с.

Число Рейнольдса определяет режим движения жидкостей (и газов) в трубах.

При Re < Re_кр, где Re_кр ≈ 2300, режим движения ламинарный, т.е. слоистый - без перемешивания жидкости и без пульсаций скоростей и давлений.

При Re > Re_кр режим течения турбулентный, т.е. с перемешиванием жидкости и с пульсациями скоростей и давлений.

Потери напора на трение по длине  определяются общей формулой Дарси
, (2.6)
где безразмерный коэффициент сопротивления трения  определяется в зависимости от режима течения:

при ламинарном режиме _л однозначно определяется число Рейнольдса, т.е.
; (2.7)
при турбулентном режиме _т помимо числа Рейнольдса зависит еще от относительной шероховатости /d, т.е., используя формулу Альтшуля
(2.8)
где Δ - высота микронеровностей стенки трубы (эквивалентная шероховатость), мм.

Указания к решению задач

Задачи данного раздела рассчитаны на применение уравнения Бернулли для потока реальной жидкости (2.3). Полагая при этом поток турбулентным, коэффициент Кориолиса можно принимать α = 1.

При применении уравнения Бернулли важно правильно выбрать те два сечения, для которых оно записывается.

В качестве сечений рекомендуется брать:

свободную поверхность жидкости в резервуаре (баке), где скорость потока v = 0;

выход в атмосферу, где р_изб = 0; р_абс = р_атм;

сечение, где присоединен тот или иной манометр, пьезометр или вакуумметр;

неподвижный воздух вдалеке от входа в трубу, в которую происходит всасывание из атмосферы.

Уравнение Бернулли рекомендуется сначала записать в общем виде, а затем переписать с заменой его членов заданными буквенными величинами и исключить члены, равные нулю.

При этом необходимо помнить следующее:

вертикальная ордината z всегда отсчитывается от произвольной горизонтальной плоскости вверх;

давление р, входящее в правую и левую части уравнения, должно быть задано в одной системе отсчета (абсолютной или избыточной);

суммарная потеря напора Σh всегда пишется в правой части уравнения Бернулли со знаком «+»;

величина Σh в общем случае складывается из местных потерь, которые можно выражать формулой Вейсбаха (2.4), и потерь на трение по длине, определяемых формулой Дарси (2.6).

Примеры решения задач

Пример 2.1. Из резервуара А, заполненного водой и находящегося под манометрическим давлением Р_м = 0,5 атм, вода подается по стальному трубопроводу длиной  = 10 м и диаметром d = 100 мм в резервуар Б на высоту Н = 2 м. Коэффициент сопротивлений крана ξ_кр = 9, каждого колена ξ_кол =0,25; ξ_вх = 0,5; ξ_вых = 1. Коэффициент гидравлического трения λ = 0,04. Определить режим течения, расход Q и скорость V воды в трубопроводе.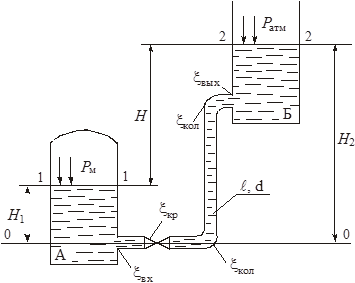



Решение:

Уравнение Бернулли в общем случае имеет вид:
. (2.9)
Первое сечение (1-1) возьмем на свободной поверхности воды в баке А, второе (2-2) - на свободной поверхности в баке Б. Плоскость сравнения совместим с осью трубопровода в месте соединения его с баком А (см. рисунок).

Давления в первом и втором сечениях возьмем абсолютные. Скоростью изменения уровней воды в баках А и Б можно пренебречь, поэтому в уравнении (2.9) v₁ = v₂ = 0. Тогда уравнение (2.9) примет вид
.
Отсюда (учитывая, что Н₂ = Н₁ + Н) получаем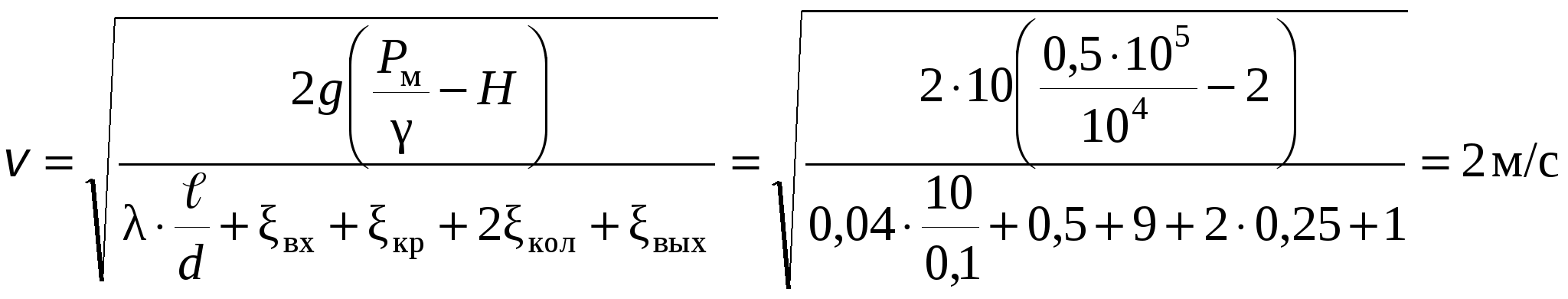

.
Режим течения определим по значению числа Рейнольдса:

Т.к. Re > 2300, следовательно, режим турбулентный.

Расход в трубе определится как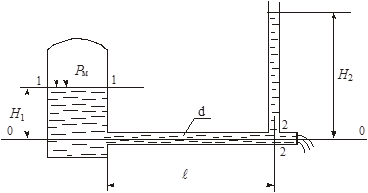





Пример 2.2. Определить расход керосина, вытекающего из бака по трубопроводу длиной  = 10 м и диаметром d = 50 мм, если избыточное давление в баке Р_м = 16 кПа, высота уровня Н₁ = 1 м, высота подъема керосина в открытом пьезометре Н₂ = 1,75 м. Труба гидравлически гладкая (шероховатость  = 0). Плотность керосина ρ = 800 кг/м³, кинематическая вязкость  = 0,025 см²/с.

Удельный вес керосина γ = ρ · g = 800 · 10 = 8000 Н/м³. Поместим первое и второе поперечные сечения потока, а также плоскость сравнения так, как показано на рисунке. Тогда уравнение Бернулли примет вид:

или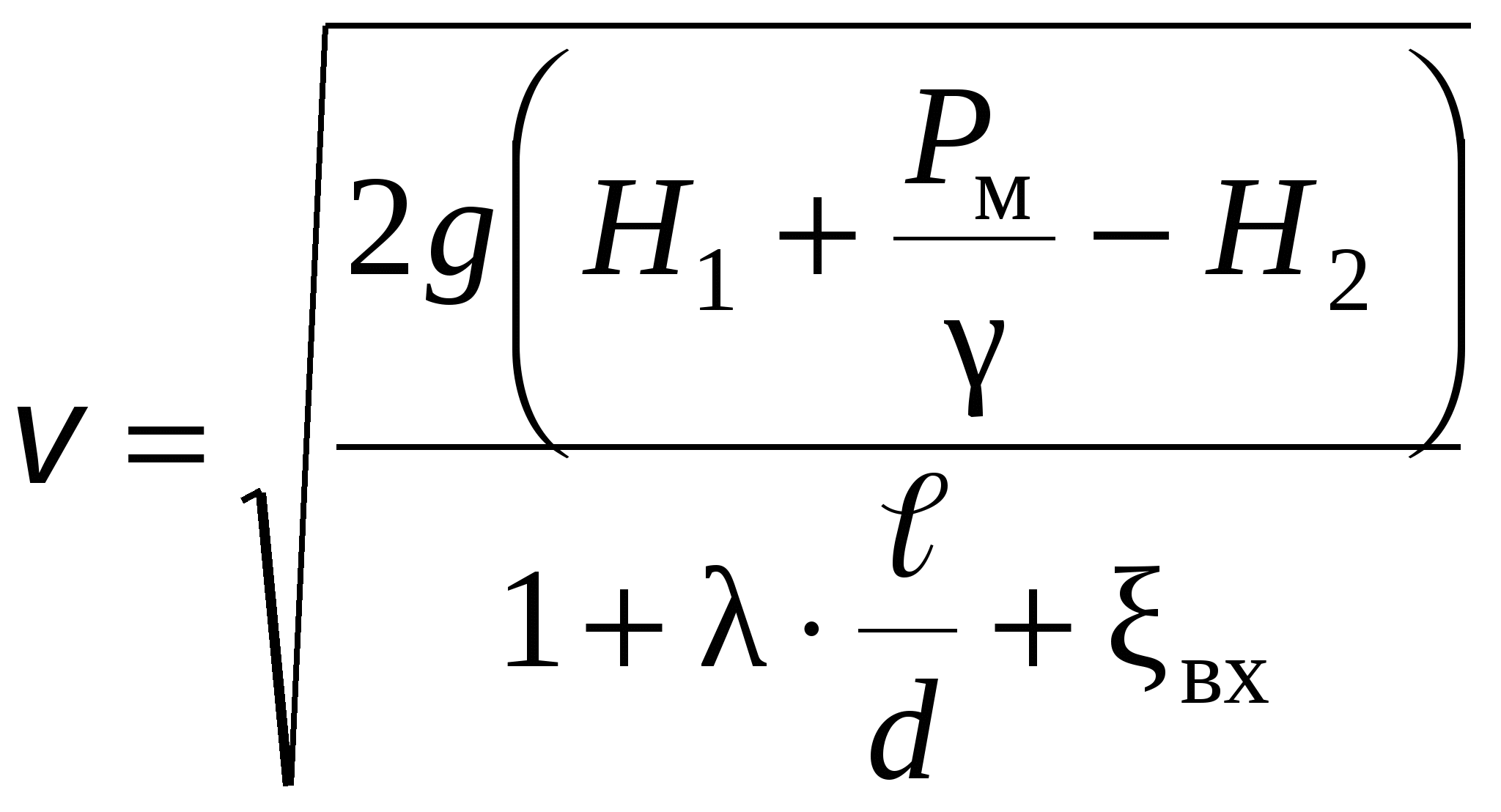
. (2.10)
Воспользоваться уравнением (2.10) мы не можем, т.к. нам неизвестно значение коэффициента гидравлического трения λ. Поэтому дальнейшее решение проводим методом последовательных приближений.

1-е приближение. Задаемся значением λ из диапазона 0,02…0,04.

Пусть λ = 0,02.

Тогда из (2.10) находим скорость: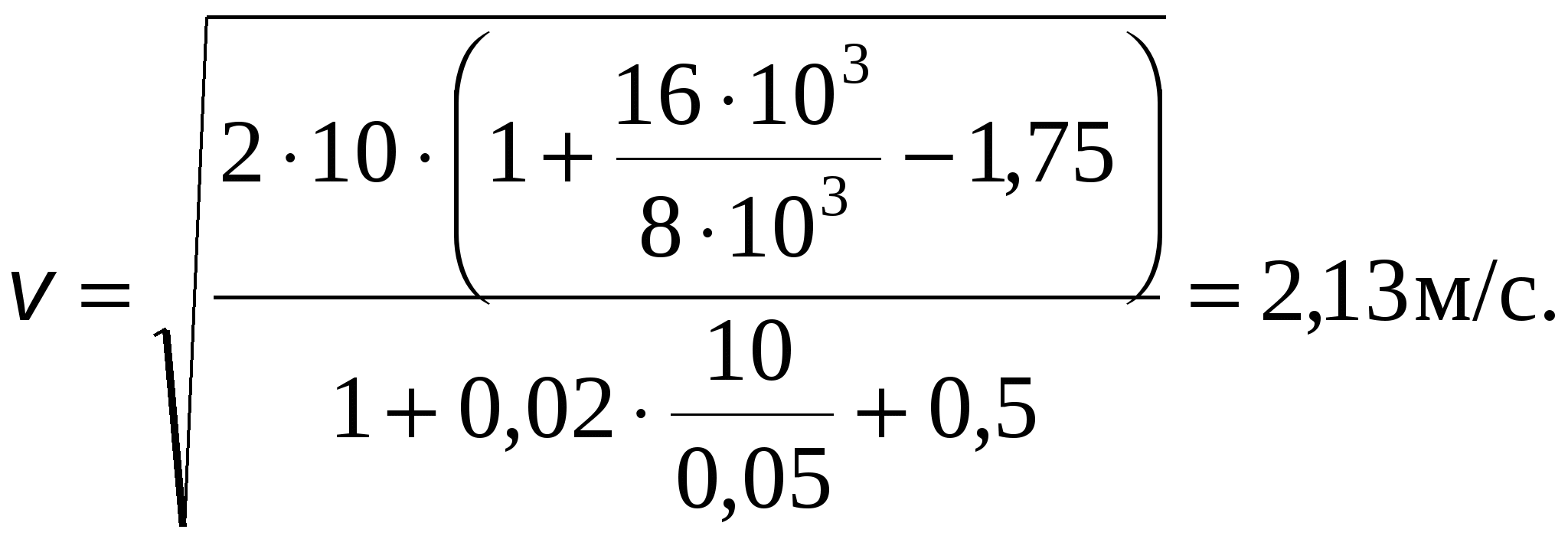

Далее определяем число Рейнольдса:

.
Поскольку режим турбулентный, а труба гладкая - коэффициент гидравлического трения λ находим по формуле Блазиуса:

Различие между принятым и получившимся значениями λ составит

Поскольку разница превышает 5%, сделаем второе приближение.

2-е приближение.

Пусть λ = 0,022.

Тогда из (2.10)




Поскольку теперь λ = λ′, приближения заканчиваем.

Расход теперь определится как

Данный метод позволяет с достаточной точностью производить инженерные расчеты.

ЗАДАЧИ К ГЛАВЕ 2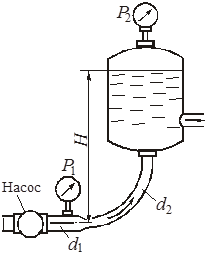




Задача 22. Насос нагнетает жидкость в напорный бак, где установились постоянный уровень на высоте Н = 2 м и постоянное избыточное давление р₂ = 0,2 МПа. Манометр, установленный на выходе из насоса на трубе диаметром d₁ = 75 мм, показывает р₁ = 0,25 МПа. Пренебрегая потерями на трение по длине, определить расход жидкости Q, если диаметр искривленной трубы, подводящей жидкости к баку, равен d₂ = 50 мм; коэффициент сопротивления этой трубы принят равным ζ = 0,5. Плотность жидкости ρ = 800 кг/м³.

Задача 23. Бензин сливается из цистерны по трубе диаметром d = 50 мм, на которой установлен кран с коэффициентом сопротивления ζ_кр = 3. Определить расход бензина при Н₁ = 1,5 м и Н₂ = 1,3 м, если в верхней части цистерны имеет место вакуум h_вак = 73,5 мм рт. ст. Потерями на трение по длине пренебречь. Плотность бензина ρ = 750 кг/м³.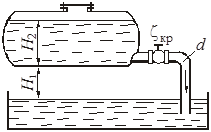




Задача 24. Вода перетекает из напорного бака А в открытый резервуар Б через вентиль с коэффициентом сопротивления ζ_в = 3 по трубе. Диаметры: d₁ = 40 мм; d₂ = 60 мм. Считая режим течения турбулентным и пренебрегая потерями на трение по длине, определить расход. Учесть потери напора при внезапных сужениях и расширениях. Высоты: Н₁ = 1 м. Н₂ = 2 м; избыточное давление в напорном баке р_о = 0,15 МПа.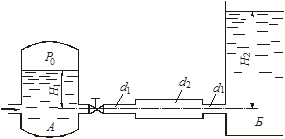








Задача 25. По длинной трубе диаметром d = 50 мм протекает жидкость (ν = 2 см²/с; ρ = 900 кг/м³). Определить расход жидкости и давление в сечении, где установлены пьезометр (h = 60 см) и трубка Пито (Н = 80 см).

У к а з а н и е. Считать, что давление перед отводом расходуется на создание скоростного напора в отводе и подъеме жидкости на высоту h.




Задача 26. Вода течет по трубе диаметром D = 20 мм, имеющей отвод (d = 8 мм). Пренебрегая потерями напора, определить расход жидкости в отводе q, если расход в основной трубе Q = 1,2 л/с; высоты Н = 2 м, h = 0,5 м. Режим течения считать турбулентным.

У к а з а н и е. Считать, что давление перед отводом расходуется на создание скоростного напора в отводе и подъеме жидкости на высоту h.




Задача 27. Масло трансформаторное из большого резервуара, в котором поддерживается постоянный ее уровень, по стальному нержавеющему трубопроводу вытекает в атмосферу. Диаметр трубопровода d = 70 мм, его горизонтальная и наклонная части одинаковой длины l = 3,4 м. Высота уровня жидкости над горизонтальной частью трубопровода равна Н = 6,2 м, конец его наклонной части находится ниже горизонтальной части на величину h = 1,5 м. Плотность масла ρ = 900 кг/м³, кинематическая вязкость ν = 0,2 см²/с. Эквивалентная шероховатость трубопровода Δ = 0,1 мм.

Определить расход Q жидкости и построить пьезометрическую и напорную линии.




Задача 28. Чему должно быть равно манометрическое давление р_м на поверхности жидкости в закрытом резервуаре А для того, чтобы обеспечить подачу керосина в количестве Q = 2,5 л/с в открытый резервуар Б? Разность уровней в резервуарах Н = 6,7 м. Чугунный старый трубопровод имеет длину 2l (l = 4,8 м) и диаметр d = 50 мм, эквивалентная шероховатость стенок Δ = 1 мм. Посредине его установлен обратный клапан К, коэффициент местного сопротивления которого ζ_кл. = 5,5. Построить пьезометрическую и напорную линии. Плотность керосина ρ = 750 кг/м³; кинематическая вязкость ν = 0,02 см²/с




Задача 29. Из бака А жидкость с плотностью ρ = 900 кг/м³ и вязкостью ν = 0,2 см²/с самотеком по алюминиевому трубопроводу длиной = 72 м попадает в производственный цех. Напор в баке А равен Н = 6 м. Каким должен быть диаметр трубопровода, чтобы обеспечивалась подача жидкости в количестве Q = 2,6 л/с при манометрическом давлении в конце трубопровода не ниже р_м = 0,2 МПа? При расчете принять, что местные потери напора составляют 20 % от потерь по длине. Построить пьезометрическую и напорную линии.

Задача 30. Из большого открытого резервуара А, в котором поддерживается постоянный уровень жидкости, по чугунному новому трубопроводу, состоящему из двух последовательно соединенных труб, глицерин течет в резервуар Б. Разность уровней жидкости в резервуарах равна Н = 6,8 м. Длина труб  = 6,8 м и ₂ = 8,2 м, а их диаметры d = 70 мм и d₂ = 50 мм. Плотность глицерина ρ = 1500 кг/м³; вязкость ν = 10 см²/с. Эквивалентная шероховатость труб Δ = 0,6 мм.

Определить расход Q жидкости, протекающей по трубопроводу. В расчетах принять, что местные потери напора составляют 15 % от потерь по длине.








Задача 31. Определить расход воды, протекающей по стальному трубопроводу в пункты 1 и 2, если напор Н в резервуаре постоянный. Длина отдельных частей трубопровода равны l = 13 м, l₁ = 13 м, l₂ = 10 м, а диаметры d = 40 мм, d₁ = 32 мм, d₂ = 32 мм. Коэффициент гидравлического трения λ принять равным 0,04. Местные потери напора в расчетах не учитывать.