Гидравлика, напор воды, решение задачи. Определить напор воды. Задача 2 Определить расход воды в водопроводной чугунной трубе переменного сечения (рис. 1) при следующих данных напор воды Н
 Скачать 259.7 Kb. Скачать 259.7 Kb.
|
 Задача 2 Определить расход воды в водопроводной чугунной трубе переменного сечения (рис. 1) при следующих данных: напор воды Н = 44 м; длины отдельных участков трубопровода L1=65 м, L2=150 м, L3=220 м; диаметры: d1=0,60 м, d2 = 1,6 м, d3=0,70 м. 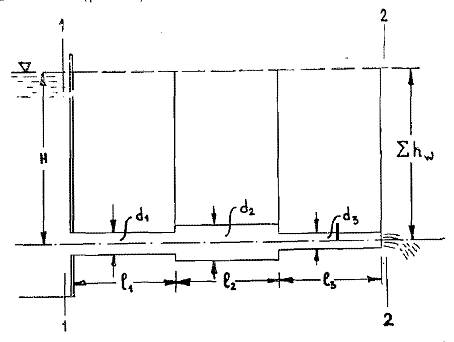 Рис. 1 По результатам расчётов построить линии гидравлического и пьезометрического уклонов. Примечание. При решении задачи следует: 1) совместив плоскость отсчёта с осью трубопровода и пренебрегая скоростью подхода, составить уравнение Бернулли для крайних створов трубопровода; 2) по учебнику пп. 3.15 и 3.16 или справочникам определить коэффициенты сопротивления (для нахождения коэффициента гидравлического трения воспользуйтесь формулой Ф. А. Шевелева, для коэффициента сопротивления при резком сужении – формулой И.Е. Идельчика); 3) принять коэффициент неравномерности распределения скоростей по сечению потока α = 1. Исходные данные: Н = 44 м; L1 = 65 м, L2 = 150 м, L3 = 220 м; d1 = 0,60 м, d2 = 1,6 м, d3 = 0,70 м. Найти: 1) расход воды Q, м3/с; 2) построить линии гидравлического (а) и пьезометрического (б) уклонов. Решение. 1) Совместим плоскость отсчёта с осью трубы ОО, принимая 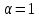 и пренебрегая скоростью подхода v0, составим уравнение Бернулли для крайних створов трубопровода 1-1, 2-2 и пренебрегая скоростью подхода v0, составим уравнение Бернулли для крайних створов трубопровода 1-1, 2-2 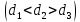 : :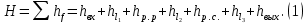 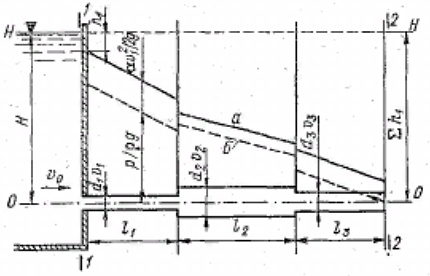 Рис. 2. К расчёту опорного трубопровода. Сечение 1-1 совпадает со свободой поверхностью жидкости в баке (свободная поверхность жидкости в резервуаре, из которого истекает жидкость) и сечение 2-2 расположено непосредственно после выхода из трубопровода (выходное сечение трубопровода). За плоскость сравнения выберем ось трубопровода. Как видно из рисунка 2 и уравнения (1), весь геометрический напор  расходуется в данной системе на местные потери (вход, резкое расширение, резкое сужение, задвижка и выход) и потери напора по длине на трение на участках расходуется в данной системе на местные потери (вход, резкое расширение, резкое сужение, задвижка и выход) и потери напора по длине на трение на участках  , ,  и и 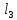 . .Местные потери напора определяются по формуле: 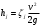 , ,где v – скорость потока, к которой отнесена потеря напора; 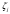 – коэффициент сопротивления, который для входа в трубопровод при острых кромках входного отверстия равен – коэффициент сопротивления, который для входа в трубопровод при острых кромках входного отверстия равен 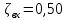 , для резкого расширения рассчитывается по формуле: , для резкого расширения рассчитывается по формуле: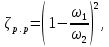 для резкого сужения по формуле: 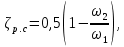 для выхода потока в атмосферу принимаем 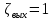 . .Потери напора по длине трубопровода определяются по формуле 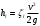 , ,где 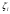 – коэффициент сопротивления, равный – коэффициент сопротивления, равный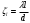 . .Здесь:l – длина участка трубопровода, м;d – его диаметр, м; λ – коэффициент гидравлического трения, который в рассматриваемом случае может быть рассчитан по формуле Шевелева: 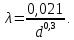 Каждое слагаемое уравнения (1) отнесено к своей скорости 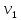 , , 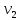 и и 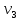 . Для дальнейшего решения этого уравнения необходимо привести его к одной скорости, например к скорости . Для дальнейшего решения этого уравнения необходимо привести его к одной скорости, например к скорости 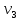 в выходном сечении. Для этой цели воспользуемся уравнением неразрывности, согласно которому в выходном сечении. Для этой цели воспользуемся уравнением неразрывности, согласно которому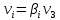 , (2) , (2)где 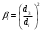 . .Уравнение (1) с учётом полученных формул можно переписать в виде: 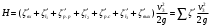 , ,где 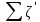 – сумма приведенных коэффициентов сопротивления; – сумма приведенных коэффициентов сопротивления;v3 – скорость потока в трубе 3, м/с; g = 9,81 м/с2 – ускорение свободного падения. 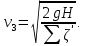 Значит, что 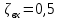 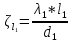 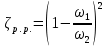 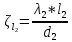 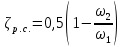 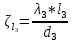 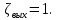 где 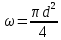 – площадь живого сечения, м2; – площадь живого сечения, м2;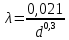 – коэффициент гидравлического трения. – коэффициент гидравлического трения.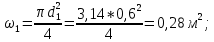 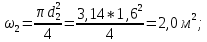 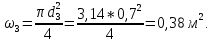 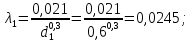 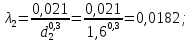 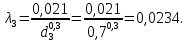 Тогда 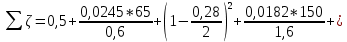 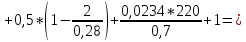 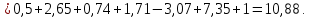 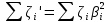 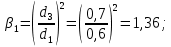 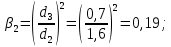 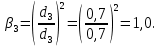 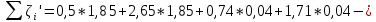 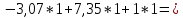 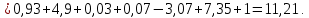 Значит 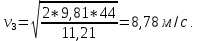 Расход воды  , одинаковый по всей длине трубопровода, рассчитывается по формуле: , одинаковый по всей длине трубопровода, рассчитывается по формуле: . .Тогда 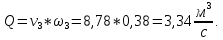 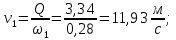 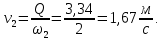 Решение задачи удобно вести по таблице. Из скоростного напора (графа 6 таблицы 1) на каждом участке трубопровода можно получить среднюю скорость потока. В графе 8 таблицы представлены значения последовательного суммирования местных и путевых потерь напора по длине трубопровода. Таблица 1. Результаты расчёта
2) Линии гидравлического и пьезометрического уклонов (см. рис. 2) строятся по данным граф 6 и 8. Для этого необходимо от плоскости отсчета  в масштабе отложить напор в масштабе отложить напор 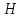 и в этом же масштабе от напорной линии и в этом же масштабе от напорной линии 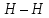 вниз отложить сначала потери напора в нарастающем итоге (графа 8), а затем скоростной напор (графа 6). вниз отложить сначала потери напора в нарастающем итоге (графа 8), а затем скоростной напор (графа 6).Строим линии гидравлического (синий цвет графика) и пьезометрического (красный цвет графика) уклонов на всех участках трубопровода. 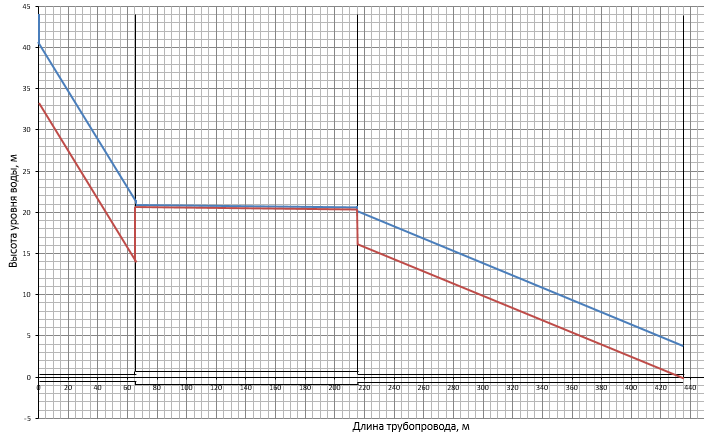 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

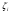
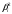
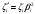
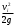
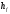
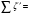 11,21
11,21