Задачи сопромат. КР №2 3 задача. Изгиб. Построение эпюр. Подбор поперечного сечения
 Скачать 4.12 Mb. Скачать 4.12 Mb.
|
|
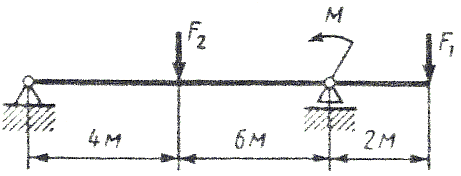
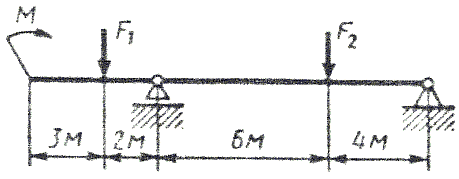
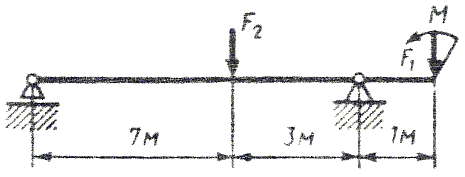
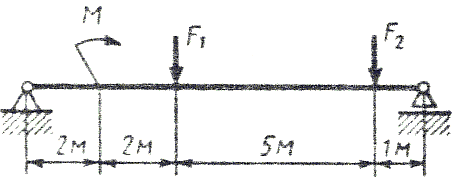
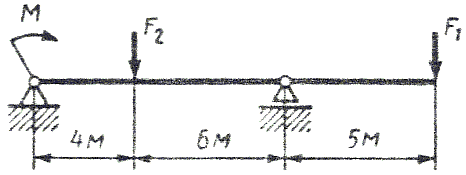
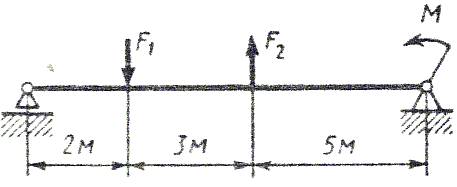
ИЗГИБ. ПОСТРОЕНИЕ ЭПЮР. ПОДБОР ПОПЕРЕЧНОГО СЕЧЕНИЯ Последовательность решения задачи 1. Определить опорные реакции и проверить правильность найденных реакций. 2. Балку разделить на участки по характерным сечениям. 3. Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюру поперечных сил. 4. Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки, вычислить изгибающие моменты в характерных сечениях и построить эпюру изгибающих моментов. 5. Для данной балки, имеющей по всей длине постоянное поперечное сечение, выполнить проектный расчет, т. к. определить Wх в опасном сечении, где изгибающий момент имеет наибольшее по модулю значение. Пример 1. Для заданной двухопорной балки (рис.1) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения в форме прямоугольника или круга, приняв для прямоугольника h/b = 1,5. Считать [σ]= 160 МПа.  Рис. 1 - Схема задачи Решение: 1. Определяем опорные реакции и проверяем их найденные значения: åМD = 0; - M1 + F2 CD + M2 + RB BD - F1 OD = 0; Σ·MB = 0; - F1 OB + M2 -F2 BC -RD BD - M1 = 0; Проверяем правильность найденных результатов: åFiy= 0; - F1+ RB+F2 +RD = -18+10+30-22 = 0 Условие равновесия å Fiy= 0 выполняется, следовательно, реакции опор найдены верно. При построении эпюр используем только истинные направления реакций опор. 2. Делим балку на участки по характерным сечениям O,B,C,D (рис. 2). 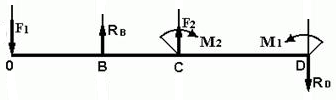 Рис. 2 - Схема истинных реакций балки и участков 3. Определяем в характерных сечениях значения поперечной силы Qy и строим эпюру слева направо (рис. 3): 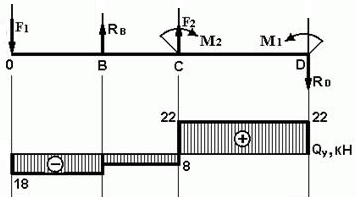 Рис. 3 - Эпюра поперечных сил 4. Вычисляем в характерных сечениях значения изгибающего момента Мх и строим эпюру (рис. 4): 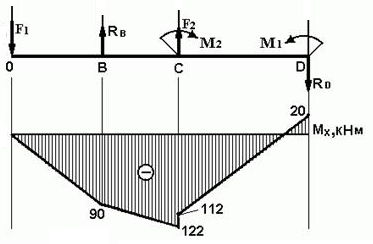 Рис. 4 - Эпюра изгибающих моментов 5. Вычисляем размеры сечения данной балки из условий прочности на изгиб: а) сечение – прямоугольник Используя формулу h= 1,5b = 1,5 127 = 190,5 мм б) сечение – круг Используя формулу Задача 1. Для заданной двухопорной балки (рис.5) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения в форме прямоугольника или круга, приняв для прямоугольника h = 2 b. Считать [σ]= 150 МПа. Таблица 1 - Исходные данные
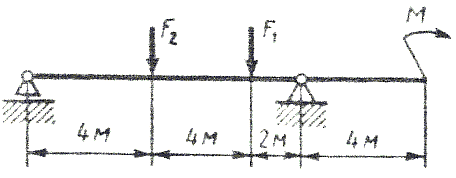
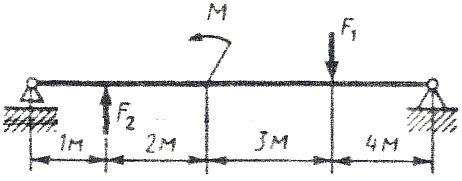
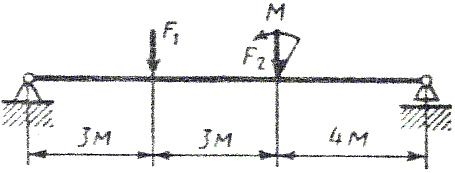
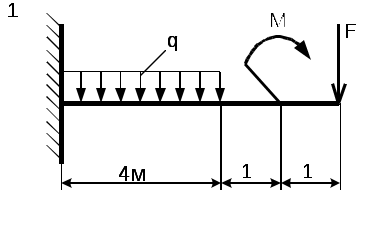
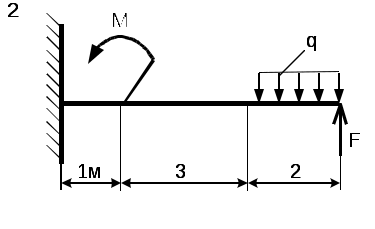
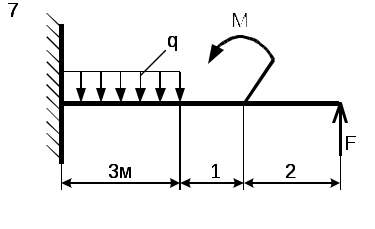
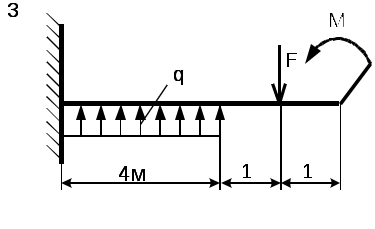
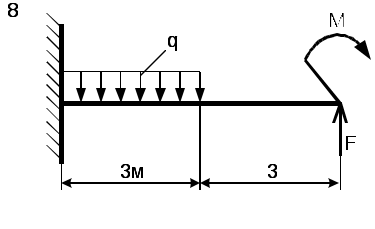
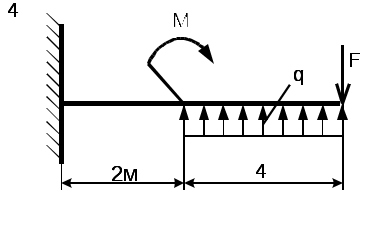
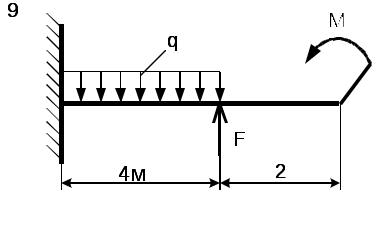
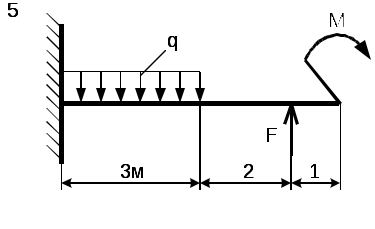
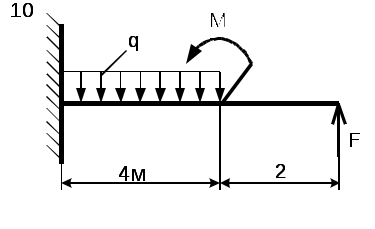
Рис. 5 - Схема задачи Задача 2. Для стальной балки, жестко защемленной одним концом и нагруженной в соответствии с рисунком 3, построить эпюры поперечных сил, изгибающих моментов и, исходя из условия прочности при [] = 160 МПа, подобрать необходимый размер поперечного сечения двутавра. Данные своего варианта брать из таблицы 2 Указание. При решении задачи использовать справочные материалы приложения А. Таблица 2 - Исходные данные
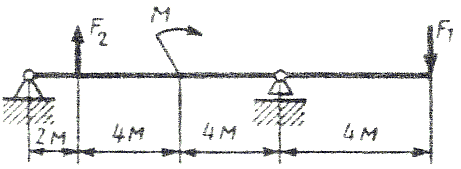
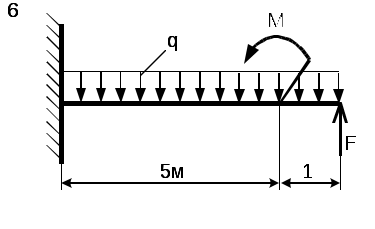
Рис. 6 - Схема задачи Приложение А (справочное) ГОСТ 8239- 89 Двутавры стальные горячекатанные. Сортамент О 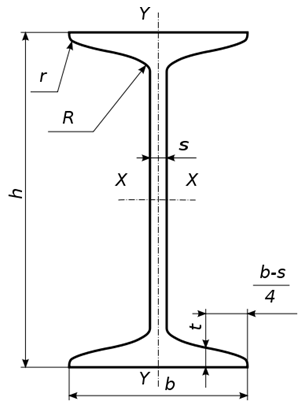 бозначение: бозначение:H - высота двутавра; B - ширина полки; S - толщина стенки; T - средняя толщина полки; R - радиус внутреннего закругления; R - радиус закругления полки I - момент инерции; W - момент сопротивления; S - статический момент полусечения; I - радиус инерции. Таблица 3
Двутавры от № 24 до № 60 не рекомендуется применять в новых разработках. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||