прекладная механика. Контрольная работа по дисциплине Прикладная механика
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Курганский государственный университет» Кафедра «Механика машин и основы конструирования» Контрольная работа по дисциплине «Прикладная механика» Выполнил: студент гр.Тз-20417 Заочной формы обучения Воденникова Анастасия Серегеевна Специальность: «Управление в технических системах» Номер зачетной книжки: №131701025 Курган 2019г Содержание:
Задание 1 Выполнить структурный анализ двух механических систем, представленных на схемах:
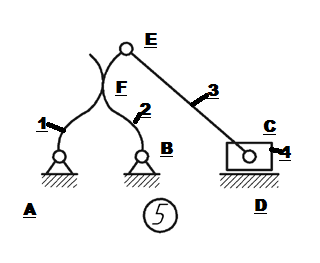 А,В,С,E – вращательные пары – 5 класса D – поступательная низшая пара – 5 класс F – высшая пара – 4 класс Определим степень подвижности механизма по формуле Чебышева: W=3n-2P(5)-P(4)= 3*4-2*5-1=1 Вывод:данная механическая система является механизмом с одним входным звеном.
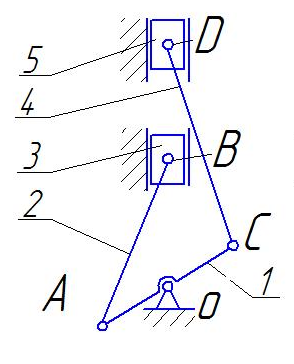 1.Определим степень подвижности механизма Для определения степени подвижности воспользуемся формулой Чебышева, так как механизм является плоским. Предварительно, установим следующие параметры, входящие в формулу. W = 3n - 2p5 - p4 = 3 n = 5 – число подвижных звеньев p5 = 7 – число кинематических пар пятого класса p4 = 0 – число кинематических пар четвертого класса Механизм имеет одну степень подвижности и одно входное звено. В качестве входного звена принят кривошип.
1 – кривошип 2 – шатун 3 – ползун 4 – шатун 5 –ползун
Условно примем стойку под цифрой 0 для удобства записей названий пар. O(0,1) – вращательная кинематическая пара 5 класса A(1,2) – вращательная кинематическая пара 5 класса B(2,3) – вращательная кинематическая пара 5 класса C(1,4) – вращательная кинематическая пара 5 класса D(4,5) – вращательная кинематическая пара 5 класса (0,3;0,5) – поступательные кинематические пары 5 класса В соответствии с теорией Ассура отделим от данного рычажного механизма входное звено со стойкой. 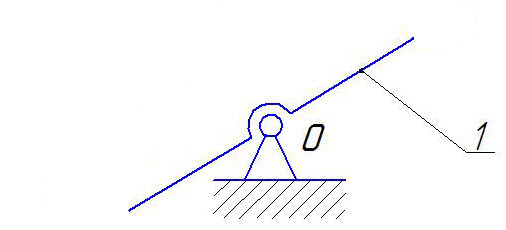 Схема механизма 1 - ого класса
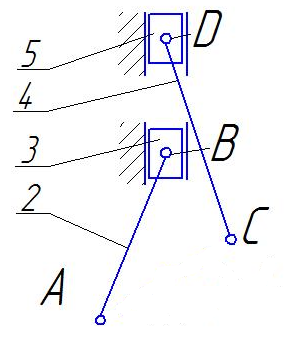 Две одинаковые оставшиеся кинематические цепи представляют собой две группы Ассура, каждая из которых имеет 2 класс, 2 порядок, 2 вид (звенья 2,3). По ним и определяется классификация всего механизма в целом. Данный механизм является механизмом 2 – ого класса. 2 класс, 2 порядок, 2 вид (2,3). 1.5 Определим вид данной системы Данная система является кривошипно-ползунным механизмом и его ранее вычисленное число степеней свободы W > 0. Задание 2 Выполнить кинематический анализ рычажного механизма, Показанного на рисунке, графическим методом на основе следующих исходных данных, изложенных в [1] ω=1м/c–1;LOA=0,025м;LAS=0,5LAB Переменные параметрыLOA/LAB= 2.5 e/LoA=0.1
μl=LOA/ [OA ]= 0.025/30=0.000833, м/ мм,
μt=2π/ωL= 0.01, c–1/мм,
μv= μS/Hvμt=0.000833/20*0.01=0.004165, м c–1/мм.
μа= μS/ Hvμt= 0.000833/20*0.004165, м c–1/мм.
Задание 3 Обеспечить заданное передаточное число редуктора, схема которого показана на рисунке 3.1. 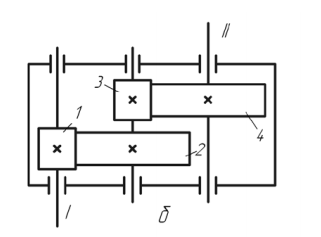 Рисунок 3.1 – двухступенчатый цилиндрический редуктор Дано: I=25 Решение Исходя из ряда стандартных передаточных чисел, принимаем для цилиндрической передачи I2 = 8, тогда передаточное число цилиндрической передачи I1 = I/I2 =25/8=3.125 Для входной ступени при I1 = 3.125 принимаем числа зубьев Z1 = 32 Число зубьев колеса Z2 = Z1·I1=3.125·32 =100 (сумма зубьев получается 100+32=132) Для выходной цилиндрической передачи при I2 = 8 принимаем число зубьев шестерни Z3 = 20. Число зубьев червячного колеса Z4 = Z3·I2 =8·20 =160 (сумма зубьев получается 20+160=160) Задание 4 Рассчитать на прочность ферму, показанную на рисунке на основании приведенных в [1] исходных данных β= 30 град F=20Н α = 90о ;L=1м; d2=30мм; [σ] = 200 МПа (сталь) Стержень круглого сечения. 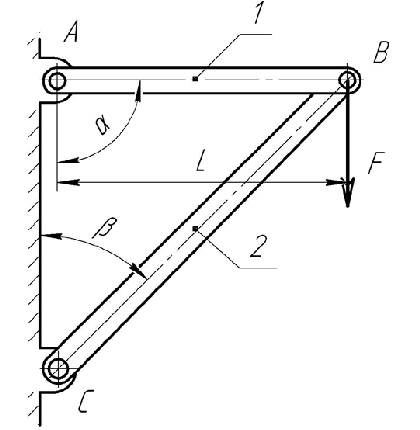 Решение: 1) рассчитать силы, действующие на стержни 1 и 2. Для этого нужно рассмотреть равновесие сил действующих в узле (шарнире) В. В векторной форме это уравнение выглядит так: F + R1 + R2 =0 в проекциях на оси X и Y: X:– R1 + R2 sin (β)=0, Y:R2 cos (β) – F =0. Откуда находим: R2= F / cos (β)=20/cos30=23.09Н R1= R2 sin (β)=23.09*sin30=11.55H 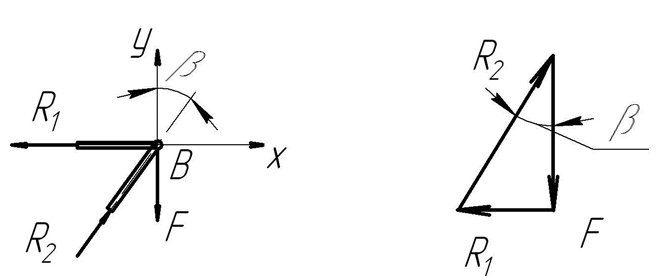 2) проверить выполнение условия прочности стержня 2, испытывающего сжатие (проверочный расчет) для этого: - найти действующее напряжение по формуле: 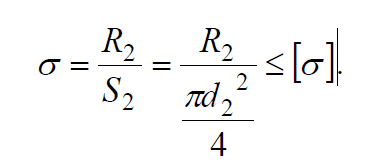 S=3.14*30*30/4=706.5 мм2 σ=23.09/706,5=0.03 МПа - расчетное напряжение значительно меньше допускаемого напряжения[σ]; - условие прочности стержней фермы выполняется. Задание 5 Выполнить проектный прочностной расчет консольной балки, показанной на рисунке для случаев ее изготовления из б) прямоугольного прутка (b=2·h), в) двутавра (№) на основании следующих исходных данных из [1] F=20Н, L=1м, [σ] = 200 МПа (сталь); плотность стали ρ =7,8 г/см3 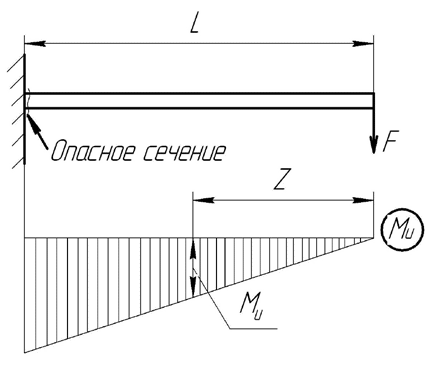 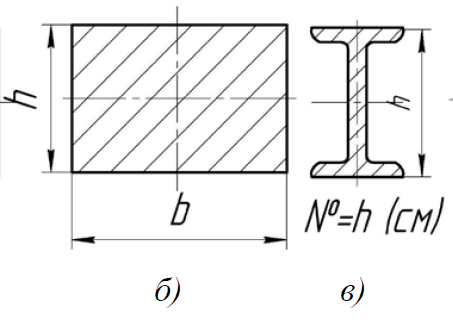
Решение:
Mu мах= FL=20*1000=20000 Н*мм
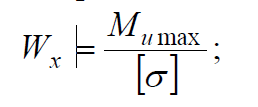 Wx= 20000/2=10000 мм(3)
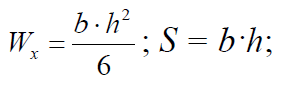 Wx= (2h*h^2)/6 h^3=Wx*3 h=31 мм b=2h=31*2=62 мм S=61*31=1922 мм2
G=S*L*p=1,922*1000*7.8=15000г, 15 кг Масса двутавра: 9,46 кг (табличное) Вывод: В результате выполненных расчетов установили, что в одинаковых условиях нагружения выгоднее применять балку двутаврового сечения. Задание 6 Выполнить ориентировочный проектный расчет вала на прочность и рассчитать шпонку на основании исходных данных, приведенных в[1]. Т=200 Нм, Количество шпонок: 1, материал сталь, 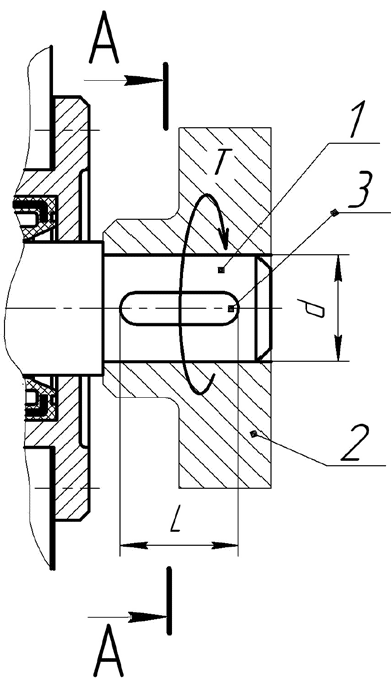 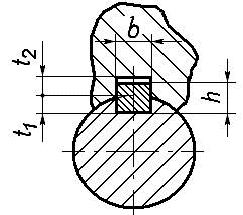
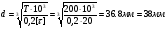 Длину консольного участка вала принимаем L= 1,5d= 55 мм
Сечение шпонки:b=10 мм, h=8 мм Глубина паза вала t1=5мм, глубина паза ступицы t2=3,3 мм Длину принимаемl=50 мм, исходя из длины консольного участка вала.
Крутящий момент передается боковыми гранями шпонки. При этом на них возникают напряжения смятия σсм, а в продольном сечении шпонки – напряжения среза τср. Допускаемое напряжение смятия [σ]см при ориентировочных расчетах для стали – [σ]см= 150-200МПа.
σсм= F1/ Sсм где F1 – окружная сила на поверхности вала, (H), приложенная к одной шпонке. F1= Т/( d/2) · z; z – количество шпонок; Sсм– площадь смятия, мм2. Sсм=(0,94h – t1) lp; lp= l – b – рабочая длина шпонки со скругленными торцами, мм. В рассматриваемом примере при z=1: F1= 200·103/ 19*1 = 10526Н; lp= 50 – 10 = 40 мм; Sсм=(0,94·8 – 5)·40 =100 мм2; σсм= 10526/100 = 105H/мм2. 105<150H/мм2. Вывод: Условие прочности шпонки на смятие выполнено. Список используемой литературы:
|
