1 Структурный анализ рычажного механизма 4 Кинематический анализ рычажного механизма 5
 Скачать 0.57 Mb. Скачать 0.57 Mb.
|
|
Содержание Задание 3 1 Структурный анализ рычажного механизма 4 2. Кинематический анализ рычажного механизма 5 3. Кинематический анализ зубчатого механизма 11 4 Геометрический расчет и построение пары прямозубых цилиндрических колес 14 Список литературы 15 Задание 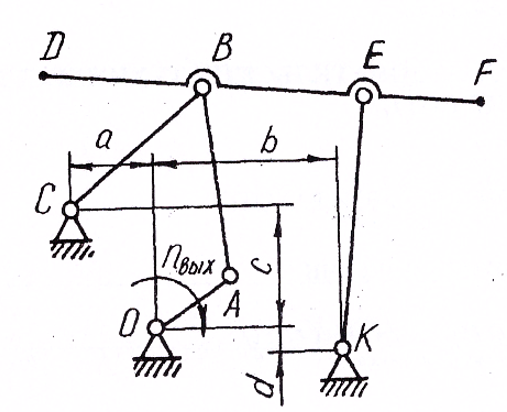 Рисунок 1. Схемы рычажного механизма Таблица 1. Исходные данные для рычажного механизма  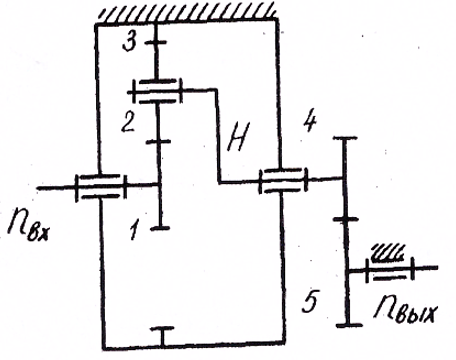 Рисунок 2. Схемы зубчатого механизма Таблица 2. Исходные данные для зубчатого механизма 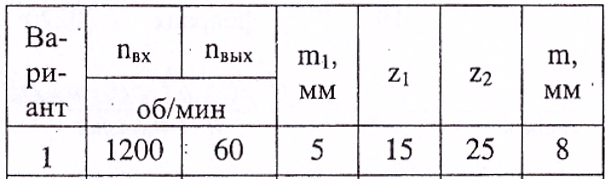 1 Структурный анализ рычажного механизма Рычажный механизм состоит из шести звеньев: 0 – неподвижное звено; 1 – кривошип; 2, 4 - шатуны; 3, 5 – кулисы. Звенья образуют следующие кинематические пары: O – вращательная, образована стойкой 0 и звеном 1; A – вращательная, образована звеньями 1 и 2; B23 – вращательная, образована звеньями 2 и 3; C – вращательная, образована стойкой 0 и звеном 3; B24 – вращательная, образована звеньями 2 и 4; E – вращательная, образована звеньями 4 и 5; K – вращательная, образована стойкой 0 и звеном 5. Все кинематические пары являются низшими. Степень подвижности механизма определяем по формуле Чебышева: 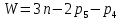 где n = 5 - число подвижных звеньев p5 = 7 - число низших кинематических пар p4 = 0 - число высших кинематических пар 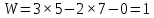 Разложим механизм на структурные группы. Звенья 4 и 5 образуют структурную группу Ассура 2го класса 2го порядка 1го вида (все три кинематические пары вращательные). Звенья 2 и 3 образуют структурную группу Ассура 2го класса 2го порядка 1го вида (все три кинематические пары вращательные). Звено 1 со стойкой 0 образуют начальный механизм 1го класса. Формула строения механизма 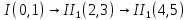 2. Кинематический анализ рычажного механизма Выполним построение плана положения механизма при заданном положении кривошипа 1 (𝜑1 = 450). Масштаб построения плана положения принимаем равным 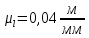 Изменим размер звена 2 механизма, так как при заданном размере механизм не собирается. Принимаем 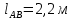 . .Для данного положения строим план скоростей. Определим скорость точки A. Так как кривошип вращается с постоянной скоростью, то скорость точки A постоянна и направлена в сторону вращения кривошипа по касательной к траектории точки A. Значение скорости точки A 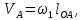 где 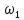 - угловая скорость звена 1. - угловая скорость звена 1.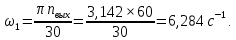 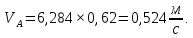 Принимаем масштабный коэффициент построения плана скоростей равным 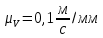 Определим длину вектора скорости точки А на плане скоростей в выбранном масштабе 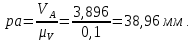 Строим вектор скорости точки A ( 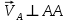 ) из полюса скоростей p. ) из полюса скоростей p.Определим скорость точки B. Для этого составим векторное уравнение скорости точки B 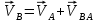 где 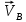 - скорость точки B; - скорость точки B;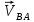 – скорость точки B относительно точки A. – скорость точки B относительно точки A.Направления векторов: 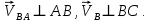 Решаем графически векторное уравнение на плане скоростей. Из плана скоростей получим 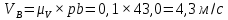 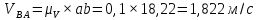 Определим скорость точки E. Для этого составим векторное уравнение скорости точки E 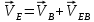 где 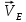 - скорость точки E; - скорость точки E;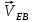 – скорость точки E относительно точки B. – скорость точки E относительно точки B.Направления векторов: 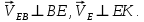 Решаем графически векторное уравнение на плане скоростей. Из плана скоростей получим 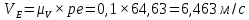 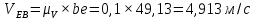 Определим скорости точек D и F. Положения точек d и f на плане скоростей определим из правила подобия, согласно которому данные точки лежат на прямой be и образуют с точками b и e отрезки bd, be, ef, которые пропорциональны длинам 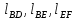 . .Составим пропорции для определения длин отрезков bd и ef. 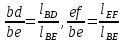 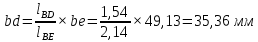 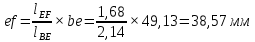 Из плана скоростей получим 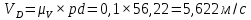 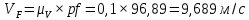 Определим угловые скорости звеньев 2, 3, 4 и 5 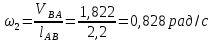 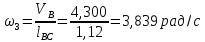 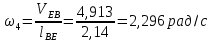 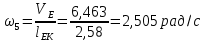 Для данного положения проведем выполним построение плана ускорений. Определим ускорение точки A. При постоянной угловой скорости ведущего звена ускорение точки A только нормальное 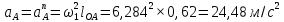 Принимаем масштабный коэффициент построения плана скоростей равным 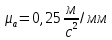 Определим длину вектора ускорения точки А на плане ускорений в выбранном масштабе 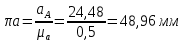 Определим ускорение точки B. Составим систему векторных уравнений 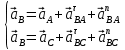 где 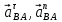 – тангенциальная и нормальная составляющая ускорения точки B относительно точки A; – тангенциальная и нормальная составляющая ускорения точки B относительно точки A;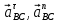 – тангенциальная и нормальная составляющая ускорения точки B относительно точки C. – тангенциальная и нормальная составляющая ускорения точки B относительно точки C.Направления векторов: 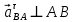 , , 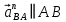 , , 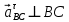 , , 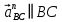 . .Определим значения нормальных ускорений 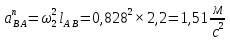 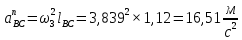 Определим длины векторов нормальных ускорений на плане ускорений в принятом масштабе 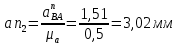 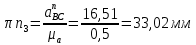 Из плана ускорений 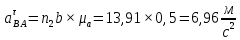 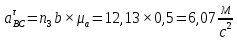 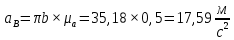 Определим ускорение точки E. Составим систему векторных уравнений 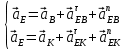 где 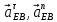 – тангенциальная и нормальная составляющая ускорения точки E относительно точки B; – тангенциальная и нормальная составляющая ускорения точки E относительно точки B;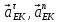 – тангенциальная и нормальная составляющая ускорения точки E относительно точки K. – тангенциальная и нормальная составляющая ускорения точки E относительно точки K.Направления векторов: 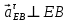 , , 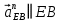 , , 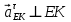 , , 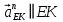 . .Определим значения нормальных ускорений 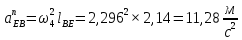 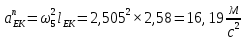 Определим длины векторов нормальных ускорений на плане ускорений в принятом масштабе 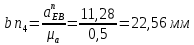 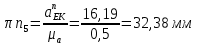 Из плана ускорений 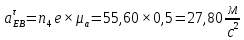 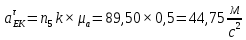 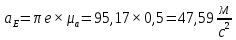 Определим ускорения точек D и F. Положения точек d и f на плане ускорений определим по аналогии с планом скоростей 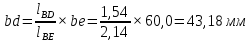 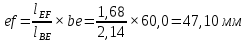 Из плана ускорений 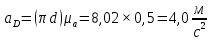 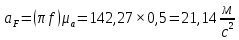 Определим угловые ускорения звеньев 2, 3, 4 и 5 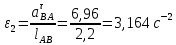 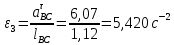 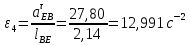 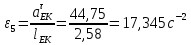 3. Кинематический анализ зубчатого механизмаОпределим передаточное отношение зубчатого редуктора 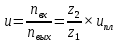 где 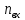 – число оборотов двигателя (входное звено), – число оборотов двигателя (входное звено), 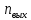 – число оборотов кулачка/кривошипа (выходное звено), – число оборотов кулачка/кривошипа (выходное звено),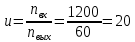 Редуктор состоит из двух ступеней: - простая зубчата передача ( 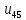 ); );- планетарный механизм ( 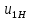 ). ).Запишем передаточное отношение редуктора через передаточные отношения ступеней 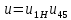 где 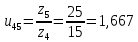 Определим передаточное отношение планетарной передачи 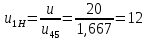 Определим число зубьев планетарной передачи. Передаточное отношение редуктора 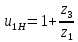 откуда выразим число зубьев колеса 3 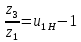  Принимаем 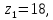 тогда тогда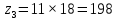 Определим число зубьев звена 2 из условия соосности 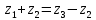 откуда 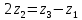 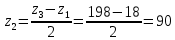 Определим количество сателлитов из условия соседства проектирования планетарного редуктора определим количество саттелитов: 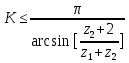 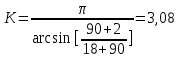 Принимаем 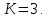 Проверим, с учетом условия сборки, количество сателлитов: 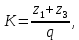 где q – любое целое число. 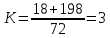 Определим радиусы колес редуктора 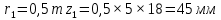 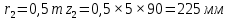 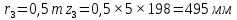 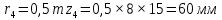 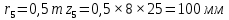 Строим схему механизма в масштабе М1:8. Строим картину линейных скоростей. Определим передаточное отношение из картины скоростей 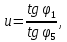 где 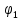 , , 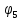 – углы наклона линий действия скоростей колес 1 и 5 соответственно. – углы наклона линий действия скоростей колес 1 и 5 соответственно.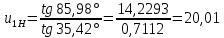 Определим погрешность при нахождении графически передаточного отношения редуктора 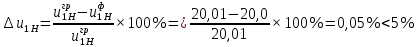 Погрешность в пределах допустимого. 4 Геометрический расчет и построение пары прямозубых цилиндрических колесОпределим коэффициенты смещения. 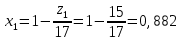 Так как 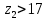 , принимаем , принимаем 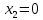 . .Радиус делительной окружности 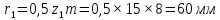 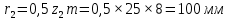 Радиус основной окружности 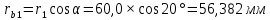 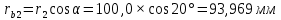 Шаг зубьев по делительной окружности 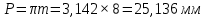 Шаг зубьев по основной окружности 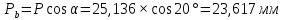 Окружная делительная толщина зуба 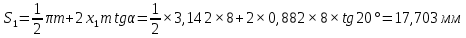 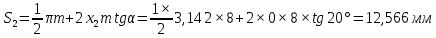 Коэффициенты суммы смещений 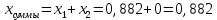 Угол зацепления 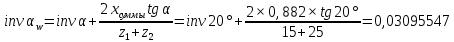 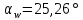 Межосевое расстояние 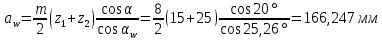 Делительное межосевое расстояние 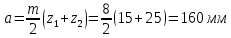 Радиус начальной окружности 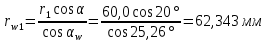 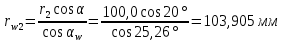 Делительное межосевое расстояние 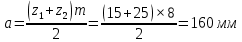 Радиус окружностей впадин 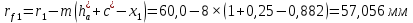 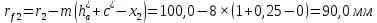 Радиусы окружностей вершин 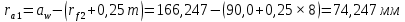 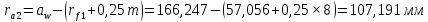 На чертеже отметим зону однопарного зацепления B1B2 = 43,14 мм. Определим коэффициент перекрытия графически 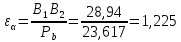 Определим коэффициент перекрытия аналитически 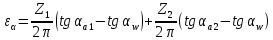 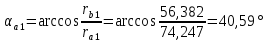 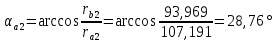 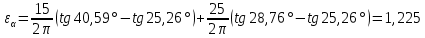 Список литературы 1. Артоболевский А.С. Теория механизмов и машин.- М.: Наука, 1988, 370 с. 3. Кожевников С.Н. Теория механизмов и машин. Учебное пособие для студентов вузов. Изд. 4-е исправленное. М., «Машиностроение», 1973. – 592 с. 3. Борисенко Л. А. Теория механизмов, машин и манипуляторов [Электронный ресурс] : учеб. пособие / Л. А. Борисенко. - Минск : Новое знание, 2011 ; Москва : ИНФРА-М, 2011. - 285 с. : ил. - (Высшее образование). - ISBN 978-985-475-430-7. 4. Григорьев А. Ю. Теория механизмов и машин. Структурный анализ механизмов [Электронный ресурс] : учеб.-метод. пособие / А. Ю. Григорьев, Ю. С. Молчанов. - Санкт-Петербург : НИУ ИТМО, 2014. - 30 с. 5. Чмиль В. П. Теория механизмов и машин [Электронный ресурс] : учеб.-метод. пособие / В. П. Чмиль. - Изд. 2-е, испр. - Санкт-Петербург : Лань, 2016. - 280 с. : ил. - (Учебники для вузов. Специальная литература). - ISBN 978-5-8114-1222-8. |
