Курс физики+вопросы. Физические основы механики элементы кинематики
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
тогда l =1/ 2nd2 v т.к. n пропорциональна давлению р, то 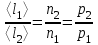 8.7.Опытное обоснование МКТ 1. Броуновское движение. 2. Опыт Штерна.  3. Опыт Ламмерт. 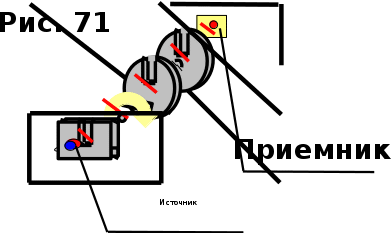 4.Опытное определение постоянной Авогадро. из (45.4) 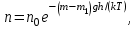 m и m0—масса част. и жидк. m = 4/3r3, m1 = 4/3r131 и 1—плотность част. и жидк. n1 и n2 — конц. частиц на уровнях h1 и h2; а k = R/NA, то 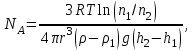 8.8. Явления переноса в термодинамически неравновесных системах 1. Теплопроводность. 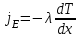 (48.1) (48.1)jE—плотность тепл. потока 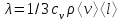 (48.2) (48.2)2. Диффузия. 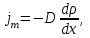 (48.3) (48.3)jm — плотность потока массы 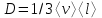 (48.4) (48.4)3.Внутреннее трение (вязкость) 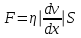 (48.5) (48.5)-динамическая вязкость(вязкость), 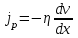 (48.6) (48.6)jp—плотность потока импульса 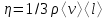 (48.7) (48.7)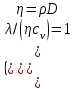 8.9. Вакуум и методы его получения. Свойства ультраразреженных газов. низкий l d средний l d высокий l > d сверхвысокий l d 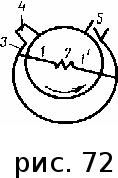 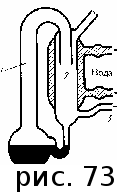   при l « d, p1 = р2 n1 v1 = n2 v2 (49.2) n=p/(kT) и v=8RT/(M) p1/p2 = T1/T2 (49.2) 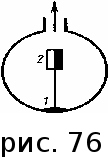 Гл.9.Основы термодинамики9.1.Число степеней свободы молекул. З-н равномерного распределения энергии по степеням свободы молекул 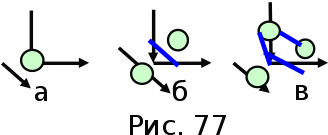 r0, J = mr20, Tвр.= Jw2/20 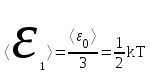 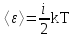 i = iпост. + iвращ. + 2iкол. 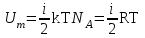 (50.1) (50.1)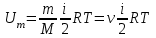 9.2.Первое начало терм-ки U = U2 U1 U = Q - A Q = U+A (51.1) dQ = dU+dA Q = dU + A (51.2) при dU = 0 A = Q 9.3.Работа газа при … 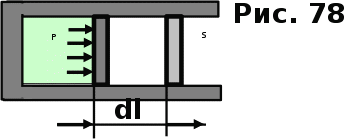 A = Fdl = pSdl = pdV A = pdV (52.1) 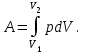 (52.2) (52.2)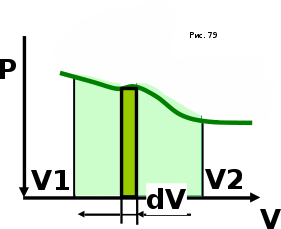 9.4. Теплоемкость 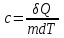 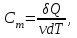 (53.1) (53.1)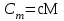 (53.2) (53.2)Сm dT = dUm + pdVm (53.3) 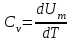 (53.4) (53.4)т.к. 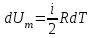 , то , тоСv = iR/2. (53.5) 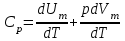 dUm/dT не зависит от вида процесса (dU газа не зависит ни от р, ни от V, а определяется лишь Т) и всегда равна Сv (см. (53.4)), и дифференцируя уравнение Клапейрона — Менделеева pVm = RT (42.4) по T , p = const), получаем уравнение Майера Сp = Сv + R (53.6) 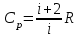 (53.7) (53.7) = Сp / Сv = ( i + 2)/i (53.8) 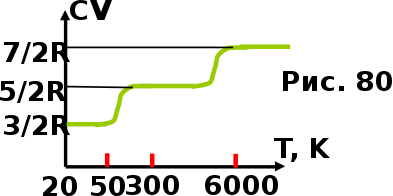 9.5. Применение первого з-на термодин. к изопроцессам И 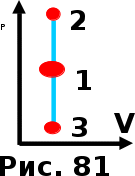 зохорный процесс (V= const) зохорный процесс (V= const)А = pdV = 0 Q = dU Т.к. dUm = Cv dT, то 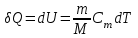 (54.1) (54.1)И 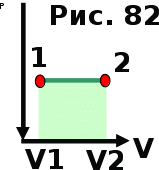 зобарный проц. зобарный проц. (р = const) 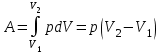 (54.2) 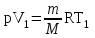 , , 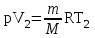 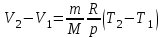 Тогда (54.2) 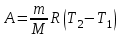 (54.3) (54.3)Из этого выражения вытекает физический смысл молярной газовой постоянной R: если T2 T1 =1 К, то для 1 моль газа R = A, т.е. R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К. 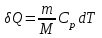 , ,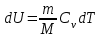 Изотерм. процесс (T = const) З-н БойляМариотта: pV = const 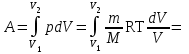 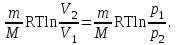 Т.к. Т = const то 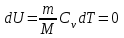 то из Q = dU + А  Q = A, т.е. (54.4) Q = A, т.е. (54.4)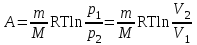   9.6.Адиабатический процесс. Политропный процесс. A = dU (55.1) из (52.1) и (53.4) 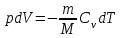 (55.2) (55.2)Дифф. 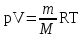 , получим , получим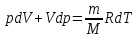 (55.3) (55.3)Исключим из (55.2) и (55.3) температуру T: 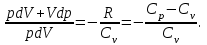 Разделив переменные и учитывая, что Ср/Сv = (см. (53.8)), найдем dp/p = - dV/V Интегрируя от p1 до p2 и от V1 до V2, а. затем потенцируя, придем к выражению 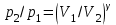 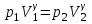 pV = const (55.4) уравнение адиабатического процесса - уравнение Пуассона исп. ур-ни Клапейрона Менделеева 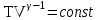 (55.5) (55.5) 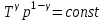 (55.6) (55.6)(55.4) (55.6) - уравнения адиабатического процесса. =Сp/Cv=cp/cv=(i + 2)/i (55.7) i = 3, = 1,67; i = 5, = 1,4.  работа, совершаемую газом в адиабатическом процессе. из(55.1) 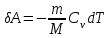   (55.8) (55.8)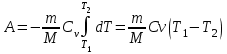 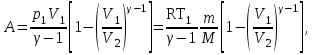 при (C = const) - политропа: 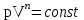 (55.9) (55.9)n = (С Ср)/(С Сv) С = 0 n = адиабата С = n =1 изотерма С = Ср n = 0 изобара С = Сv n = ± изохора 9.7.Круговой процесс (цикл). Обратимые и необратимые процессы. 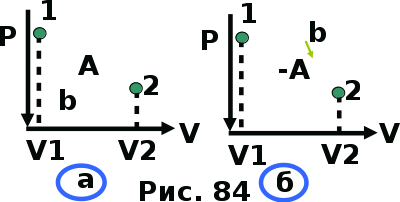 A=pdV>0 A=pdV<0 Q = U + A = A (56.1) Q = Q1 – Q2, 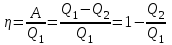 (56.2) (56.2)9.7. Энтропия, ее статистическое толкование и связь с термодинам. вероятностью 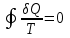 (57.1) (57.1)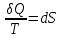 (57.2) (57.2)S = 0 (57.3) S > 0 (57.4) S 0 (57.5) 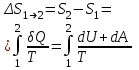 (57.6) (57.6)найдем изменение энтропии в процессах идеального газа. 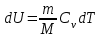 , ,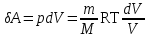 , ,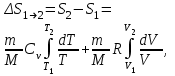  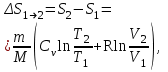 (57.7) (57.7)адиабата Q=0, S=0 и S= const, изотерма (T1 = T2 ) 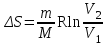 изохора (V1 = V2) 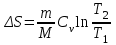 S = klnW (57.8) 9.9.Второе начало термодин. любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает теорема Нернста Планка: 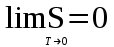 9.10. Тепловые двигатели и холодильные машины 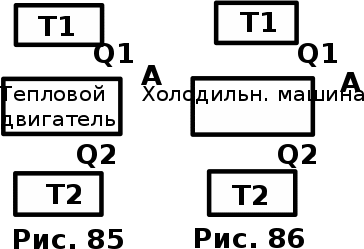 Цикл Карно и его к.п.д. для идеального двигателя.  1 2 (59.1) 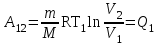 2 3 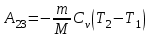 3 4 (59.2) 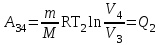 41 41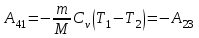 A=A12+A23+А34+А41= =Q1+A23 Q2A23= Q1Q2 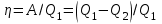 Применив уравнение (55.5) для адиабат 2 3 и 4 1, получим 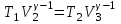 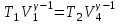 Откуда V2 / V1 = V3 / V4 (59.3) 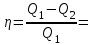  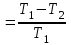 (59.4) (59.4)T1=400 К T2 = 300 К = 0,25 T =500 К T2 = 2500 К = 0,50 T2 / T1 = Q2 / Q1 (59.5) Гл. 10. Реальные газы, жидкости и твердые тела 10.1. Силы и потенциал. энергия межмолекулярного взаимодействия. 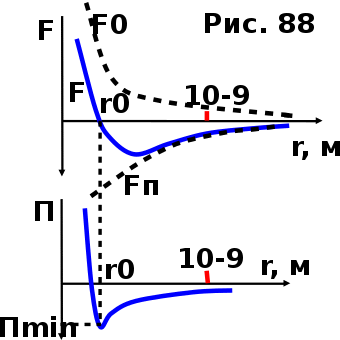 A = Fdr = dП (60.1) 10.2.Ур-е Ван-дер-Ваальса 1 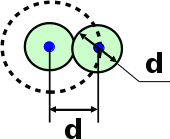 .Учет собственного объема молекул .Учет собственного объема молекул Vm—b 2.Учет притяжения молекул. p=/Vm2 (61-1) (p+/Vm2)(Vm-b)=RT (61.2) т.к. = m/M и V=Vm (p + 2/V2 )( V/ - b) = RT p + 2/V2 )( V - b) = RT где и b — постоянные для каждого газа величины, определяемые опытным путем 10.3.ИЗОТЕРМЫ ВАН-ДЕР-ВААЛЬСА И ИХ АНАЛИЗ 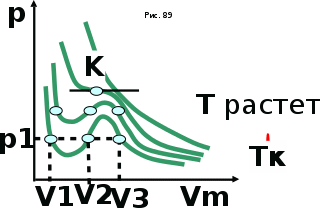 р 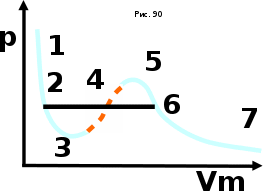 V3 -(RT+pb)V2+Vm-b=0 (62.1) V3 -(RT+pb)V2+Vm-b=0 (62.1)pкV3(RTк+pкb)V2+Vb= 0 (62.2) pк(V–Vк)3=0 (62.2) или pкV3–3pкVкV2–3pкVк2V– –pкVк = 0 (62.3) Т. к. ур-ния (62.2) и (62.3) тождественны, pкVк3 = b, 3pкVк2 = , 3pкVк = RTк + pкb, Vк = 3b, pк = /(27 b2 ), Tк = 8/(27Rb). 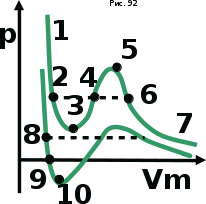 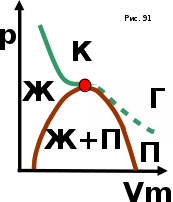 10.4. Внутренняя энергия реального газа p=/Vm2 A = p'dVm = П , или П = /Vm2dV, откуда П = /Vm Um = СvТ /Vm (63.1) если Q=0 и A=0, то Q = (U2 — U1) + A получим U2 = U1 (63.2) для и.г. U2=U1 означает T1=T2 для р.г. U1=СvТ1/V1 и U2=СvТ2/V2 (63.3)  Так как V2 V1, то T1 Т2, т. e. реальный газ при адиабатическом расширении в вакуум охлаждается. 10.5. Эффект Джоуля — Томсона. Если идеальный газ адиабатически расширяется и совершает при этом работу, то он охлаждается, так как работа в данном случае совершается за счет его внутренней энергии (см. ). Подобный процесс, но с реальным газом — адиабатическое расширение реального газа с совершением внешними силами положительной работы — осуществили английские физики Дж. Джоуль (1818—1889) и У. Томсон (лорд Кельвин, 1824—1907). Р 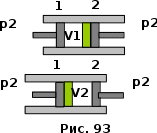 ассмотрим эффект Джоуля — Томсона. На рис. 93 представлена схема их опыта. В теплоизолированной трубке с пористой перегородкой находятся два поршня, которые могут перемещаться без трения. Пусть сначала слева от перегородки газ под поршнем 1 находится под давлением p1, занимает объем V1 при температуре T1, а справа газ отсутствует (поршень 2 придвинут к перегородке). После прохождения газа через пористую перегородку в правой части газ характеризуется параметрами p2, V2, T2. Давления p1 и p2 поддерживаются постоянными (p1 p2 ). ассмотрим эффект Джоуля — Томсона. На рис. 93 представлена схема их опыта. В теплоизолированной трубке с пористой перегородкой находятся два поршня, которые могут перемещаться без трения. Пусть сначала слева от перегородки газ под поршнем 1 находится под давлением p1, занимает объем V1 при температуре T1, а справа газ отсутствует (поршень 2 придвинут к перегородке). После прохождения газа через пористую перегородку в правой части газ характеризуется параметрами p2, V2, T2. Давления p1 и p2 поддерживаются постоянными (p1 p2 ).Так как расширение газа происходит без теплообмена с окружающей средой (адиабатически), то на основании первого начала термодинамики Q = (U1 – U2) + A = 0 (64.1) Внешняя работа, совершаема газом, состоит из положительной работы при движении поршня 2 ( A2 = p2V2 ) и отрицательной при движении поршня 1 ( A1 = p1V1 ), т. е. A = A2 – A1. Подставляя выражения для работ в формулу (64.1), получаем U1 + p1V1 = U2 + p2V2 (64.2) Таким образом, в опыте Джоуля Томсона сохраняется (остается неизменной) величина U + pV. Она является функцией состояния и называется энтальпией. Ради простоты рассмотрим 1 моль газа. Подставляя в формулу (64.2) выражение (63.3) и рассчитанные из уравнения Ван-дер-Ваальса (61.2) значения p1V1 иp2V2 (символ «m» опять опускаем) и производя элементарные преобразования, получаем 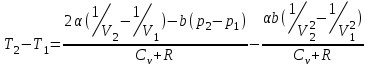 (64.3) (64.3)Из выражения (64.3) следует, что знак разности (T2 – T1) зависит от того, какая из поправок Ван-дер-Ваальса играет большую роль. Проанализируем данное выражение, сделав допущение, что p2 p1 и V2 V1 0 — не учитываем силы притяжения между молекулами, а учитываем лишь размеры самих молекул. Тогда 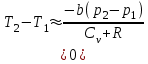 т. е. газ в данном случае нагревается; b 0 — не учитываем размеров молекул, а учитываем лишь силы притяжения между молекулами. Тогда 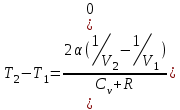 т. е. газ в данном случае охлаждается; учитываем обе поправки. Подставив в выражение (64.3) вычисленное из уравнения Ван-дер-Ваальса (61.2) значение p1 имеем 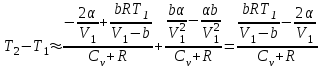 (64.4) (64.4)т. е. знак разности температур зависит от значений начального объема V1 и начальной температуры T1. Изменение температуры реального газа в результате его адиабатического расширения, или, как говорят, адиабатического дросселирования — медленного прохождения газа под действием перепада давления сквозь дроссель (например, пористую перегородку), называется эффектом Джоуля — Томсона. Эффект Джоуля — Томсона принято называть положительным, если газ в процессе дросселирования охлаждается (T<0), и отрицательным, если газ нагревается (T>0). В зависимости от условий дросселирования для одного и того же газа эффект Джоуля — Томсона может быть как положительным, так и отрицательным. Температура, при которой (для данного давления) происходит изменение знака эффекта Джоуля — Томсона, называется температурой инверсии. Ее зависимость от объема получим, приравняв выражение (64.4) нулю: 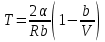 (64.5) (64.5)К  ривая, определяемая уравнением (64.5), — кривая инверсии — приведена на рис. 94. Область выше этой кривой соответствует отрицательному эффекту Джоуля — Томсона, ниже — положительному. Отметим, что при больших перепадах давления на дросселе температура газа изменяется значительно. Так, при дросселировании от 20 до 0,1 МПа и начальной температуре 17°С воздух охлаждается на 35° С. ривая, определяемая уравнением (64.5), — кривая инверсии — приведена на рис. 94. Область выше этой кривой соответствует отрицательному эффекту Джоуля — Томсона, ниже — положительному. Отметим, что при больших перепадах давления на дросселе температура газа изменяется значительно. Так, при дросселировании от 20 до 0,1 МПа и начальной температуре 17°С воздух охлаждается на 35° С.Эффект Джоуля — Томсона обусловлен отклонением газа от идеальности. В самом деле, для моля идеального газа pVm=RT, поэтому выражение (64.2) примет вид Сv Т1 + RT1 =. Cv T2 + RT2, откуда следует, что T1 = T2.  10.6. Сжижение газа Превращение любого газа в жидкость — сжижение газа возможно лишь при температуре ниже критической (см. ). При ранних попытках сжижения газов оказалось, что некоторые газы (С12, СО2, МН3) легко сжижались изотермическим сжатием, а целый ряд газов (02, N2, H2, Не) сжижению не поддавался. Подобные неудачные попытки объяснил Д. И. Менделеев, показавший, что сжижение этих газов производилось при температуре, большей критической, и поэтому заранее было обречено на неудачу. Впоследствии удалось получить жидкий кислород, азот и водород (их критические температуры равны соответственно 154,4, 126,1 и 33 К), а в 1908 г. нидерландский физик Г. Камерлинг-Оннес (1853-1926) добился сжижения гелия, имеющего самую низкую критическую температуру (5,3 К). Для сжижения газов чаще применяются два промышленных метода, в основе которых используется либо эффект Джоуля — Томсона, либо охлаждение газа при совершении им работы. Схема одной из установок, в которой используется эффект Джоуля—Томсона, — машины Линде представлена на рис. 95. Воздух в компрессоре (К) сжимается до давления в десятки мегапаскаль и охлаждается в холодильнике (X) до температуры ниже температуры инверсии, в результате чего при дальнейшем расширении газа наблюдается положительный эффект Джоуля — Томсона (охлаждение газа при его расширении). Затем сжатый воздух проходит по внутренней трубе теплообменника (ТО) и пропускается через дроссель (Др), при этом он сильно расширяется и охлаждается. Расширившийся воздух вновь засасывается по внешней трубе теплообменника, |
