Курс физики+вопросы. Физические основы механики элементы кинематики
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И ЕДИНИЦЫ ВЕЛИЧИН1.1. Физические величиныФИзическая величина — 1.1.1. Скалярные и векторные величины скалярная — векторная — коллинеарные векторы — орт-векторЫ —. Аксиальные (псевдо-векторы) — 1.1.2. Основные, дополнительные и производные величины
Основные величины — (Система Интернациональная - СИ) метр килограмм секунда ампер кельвин моль кандела Дополнительные величины — радиан и стерадиан Метр (м) — длина пути, проходимого плоской электромагнитной волной в вакууме за 1/299792458 c. Стерадиан (ср) — телесный угол с вершиной в центре сферы, вырезающий на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы производные величины — размерность — v =s/t dim v = LT-1, v = 1мс-1
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИГлава 1. Элементы кинематики Модели в механике. Система отсчета. Траектория, длина пути, вектор перемещения. Механика — Механическое движение — Классическая механика — релятивистская механика — квантовая механика — Классическая механика включает: кинематика — , динамика —, статика —. Материальная точка — Система материальных точек — Абсолютно твердое тело — Поступательное движение — Вращательное движение — Т 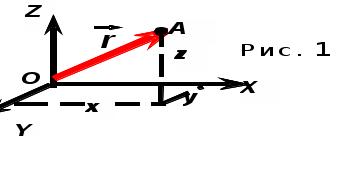 ело отсчета —
Число степеней свободы — Траектория движения материальной точки — прямолинейная или криволинейная . 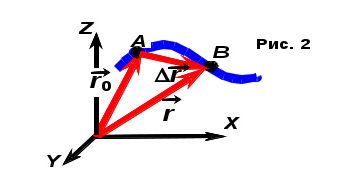 длина пути — s = s(t) перемещение —    r = r - r0, r = r - r0,при прямолинейном движении  r = s r = s1.2. Скорость 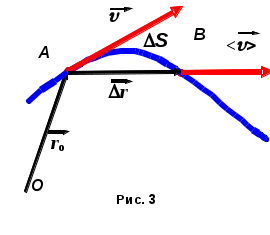 П  усть t → 0, s, r усть t → 0, s, rВектор средней скорости v —   v = r/t (2.1) v = r/t (2.1) мгновенная скорость —    v = lim(r/t) = dr/dt v = lim(r/t) = dr/dtt0   = v = lim(r/t) = = v = lim(r/t) =  t0 t0lim(r/t) =lim(s/t) =ds/dt t0 t0 = ds/dt (2.2) средняя скорость неравномерного движения: = ds/dt   > v ; s > r > v ; s > r в случае прямолинейного движения  s = r s = r если выражение ds = dt проинтегрировать, то: t+t s = dt (2.3) t при = const t+t s = dt = t t Длина пути t2 s = (t)dt t1 1.3. Ускорение и его составляющие ускорение — 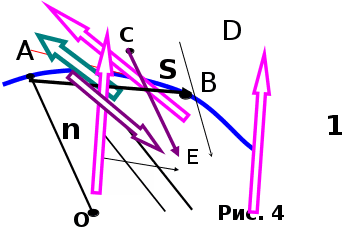 среднее ускорение —   α = v/t α = v/tМ  гновенное ускорение α — гновенное ускорение α —    α = lim α = lim(v/t) = dv/dt α = lim α = lim(v/t) = dv/dtt0 t0 У  скорение α скорение α   α = dv/dt α = dv/dtп  еренесем вектор v1 в точку А еренесем вектор v1 в точку А и  найдем v найдем vр  азложим v на две составляющие: азложим v на две составляющие:  v = 1 - и vn v = 1 - и vnТангенциальная составляющая ускорения:α = lim( v/t) = lim( v/t ) = t0 t0 = dv/dt из подобия треугольников АОВ и ЕАD следует, что vn/АВ = 1/r, но AB= • t тогда vn/t =•1/r при t0 получим v1v, угол ЕАД 0, треугольник EADравнобедренному, угол ADE900. с   ледовательно, при t0 векторы vn и v оказываются взаимно перпендикулярными. ледовательно, при t0 векторы vn и v оказываются взаимно перпендикулярными.Вторая составляющая ускорения, равная   α n = lim (vn/t) = v2/r α n = lim (vn/t) = v2/rt0 нормальная составляющая ускорения (центростремительное ускорение) — Полное ускорение — 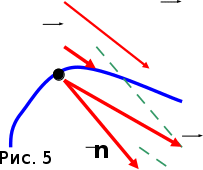 α     = dv/dt = α n + α = dv/dt = α n + α Классификация движения
рассмотрим случай (2) подробнее: α = α = /t =(2 - 1)/(t2 - t1) Если начальный момент времени t1=0, а начальная скорость 1=0, то, обозначив t2 = t и 2 = , получим α = ( - 0)/t, откуда = 0 + α •t. интегрируя, получим: t t s = dt =(0 + α •t)dt 0 0 =0•t + α •t2/2 1.4. Угловая скорость и угловое ускорение  за t точка переместится на . М  одуль вектора — одуль вектора —правило правого винта — псевдовектор (аксиальными) — Угловая скорость —    = lim (/t) = d/dt = lim (/t) = d/dt t0 В  ектор — ектор —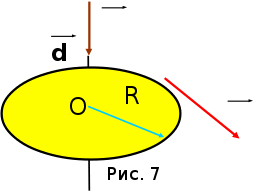 Размерность угловой скорости d  im =Т-1, (рад/с) im =Т-1, (рад/с)Линейная скорость (см.рис. 6): = lim(s/t) = lim (R•/t) = t0 t0 =R•lim(/t) = R•, t0 т.е. = R• В векторном виде v   = [ • R]. = [ • R].При =const - вращение равномерное. Период вращения Т -— т.к. t = Т и = 2, то = 2/T, и T = 2/. частота вращения -— n = 1/Т = /(2), откуда = n2 Угловое ускорение —   = d / dt = d / dtвектор углового ускорения —
Тангенциальная составляющая — α = d(R/dt) = R•d/dt = R• lim(s/t) = lim (R•/t) = t0 t0 = R• lim(/t) = R• t0 Нормальная составляющая — αn = 2/R = 2R2/R = 2R s = R•, = R•, α = R•, αn = 2•R равнопеременное движение — (=const) = 0 + •t, = 0•t + •t2/2 Коля ловил девчонок, окунал их в лужу и старательно измерял глубину погружения каждой девчонки, а Толя только стоял рядышком и смотрел, как девчонки барахтаются. Чем отличаются Колины действия от Толиных, и как такие действия называют физики?  ОТВЕТ: И физики, и химики назовут Колины и Толины действия хулиганством и надают по шее обоим. Но надо признать, что с точки зрения бесстрастной науки Толя производил наблюдения, а Коля ставил опыты. Глава 2. Динамика 2.1.Первый з-н Ньютона. Масса. Сила. 2.2.Второй з-н Ньютона F (m = const) (6.1) 1/m(F = const) (6.2) Из (6.1) и (6.2) = F/m (6.3) : в СИ k = 1, тогда    F=m = mdv/dt (6.4) F=m = mdv/dt (6.4)  F= dmv/dt (6.5) F= dmv/dt (6.5)  p=mv (6.6) p=mv (6.6)   F= dp/dt (6.7) F= dp/dt (6.7)Единица силы в СИ —(Н): 1 Н = 1 кг*м/с2 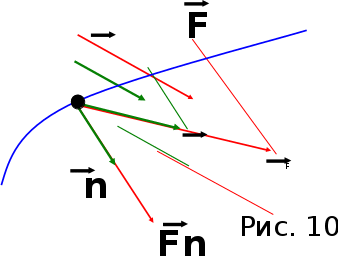 используя = dv/dt, n = v2/r и v = R •w, получим: F = m = mdv/dt Fn =nm = m v2/r 2.3.Третий закон Ньютона   F12 = - F21 (7.1) F12 = - F21 (7.1)2.4. Силы трения 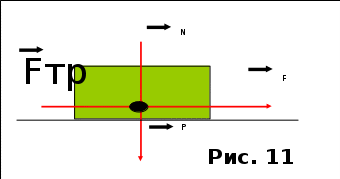 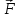 F > Fтр. Fтр.=f·N f —коэфф. тр. cкольж. 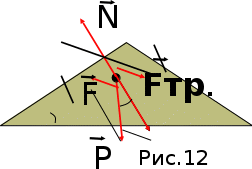 F > Fтр норм. скольж. F = Fтp, Р·sin= f·N = f·P·cos0, откуда f = tg0 Для гладких поверхн. Fтp = fист(N+S·p0), Fтp = fк·N/r (8.1) r — радиус катящегося тела; fк —- коэффициент трения качения 2.5.З-н сохр. импульса. Центр масс. Механическая система – Внутренние силы – Внешние силы – Система из n тел Пусть 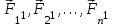 — равнодейст. внутр. сил, 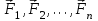 — равнодейст. внешн. сил. — равнодейст. внешн. сил.2-ой з-н Ньютона 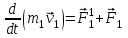 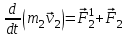 ................................. 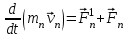 Складывая получаем 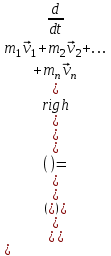 т.к. сумма внутр. сил =0, то 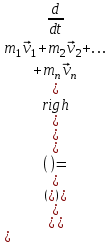 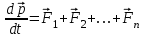 (9.1) (9.1)где  —импульс —импульс Для замкнутой системы 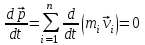 , , т.е. 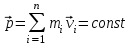 . .- з-н сохранения импульса Ц  ентр масс ентр масс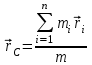 , , 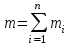 Скорость центра масс 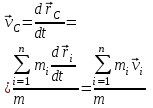 . .Т.к. 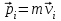 ,а ,а 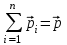 , , то 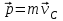 (9.2) (9.2)Подставив (9.2) в (9.1), получим (9.3) 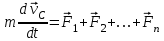 2.6. Ур-ние движ. тела переменной массы  t , m, v, t , m, v,dt, dm, m-dm, v+dv u = const Изменение импульса за dt 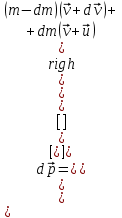 Тогда Тогда 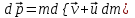 dmdv - малый в.п. м. Если действ. внешне силы, то 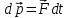 т.е. 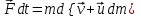 , , или 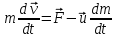 (10.1) (10.1)ур. движ. тела перем. массы 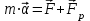 (10.2) (10.2)Полагая F=0, получим 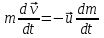 откуда 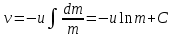 . .Если v0=0, а масса - m0, то 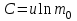 c-но, 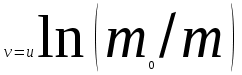 (10.3) (10.3)Гл 3. Работа и энергия. 3.1.Энергия, работа, мощность. A=Fs S = FS сos (11.1) 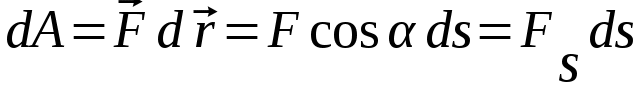 - угол между - угол между 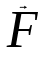 и и 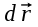 ; ; 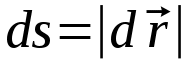 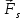 — проек. — проек. 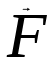 на на 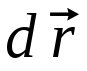        V Fs 2 F    1 dr  Рис. 13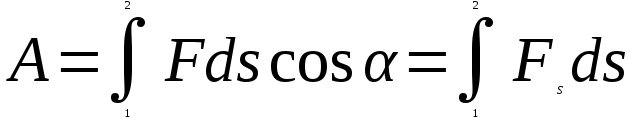 (11.2) (11.2)           dA 1 Fs 2 A ds S Рис. 14 если F=const и =const, то 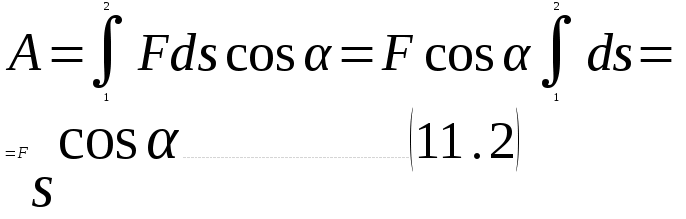 (11.2) при < /2, A> 0, 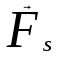 — —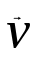 если > /2, А< 0 если =/2 А=0 джоуль (Дж): 1Дж =1Н*м 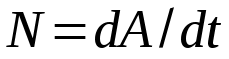 (11.3) (11.3)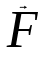 — — 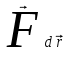 , то , то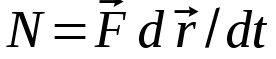 ватт (Вт): 1 Вт = 1 Дж/с. 3.2. Кинетическая и потенциальная энергии dA = dT. вт. з-н Ньютона F = mdv/dt, и dr то 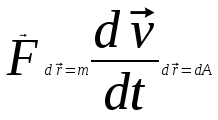 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

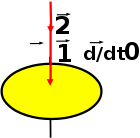
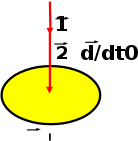
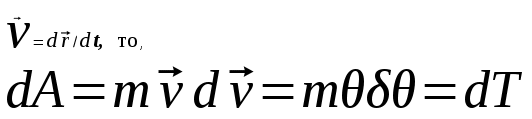
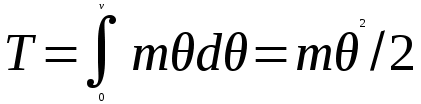
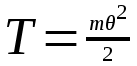 (12.1)
(12.1)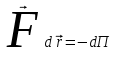 (12.3)
(12.3)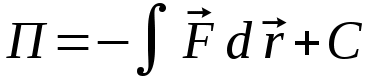
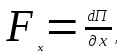
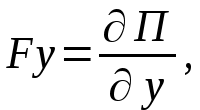
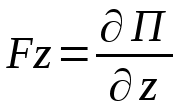 ,
,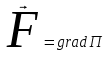 (12.4)
(12.4)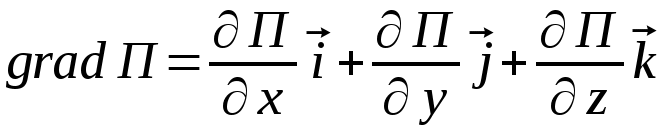
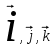 - един. векторы (12.5)
- един. векторы (12.5)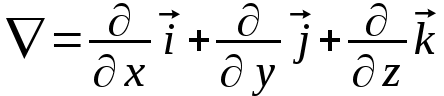 (12.5)
(12.5)
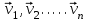
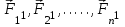
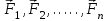
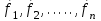
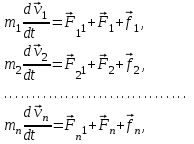
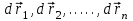
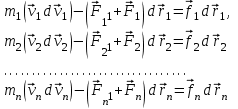
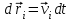 ,
, 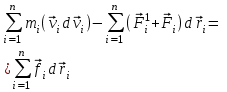
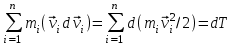 гдеdT - приращение кинетической энергии системы.
гдеdT - приращение кинетической энергии системы. 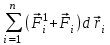 равенdПсм.(12.2)
равенdПсм.(12.2)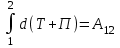
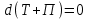
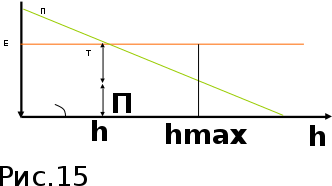 .4. Графическое
.4. Графическое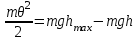
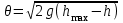
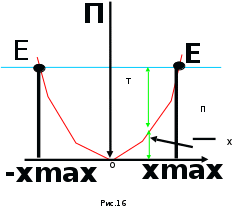
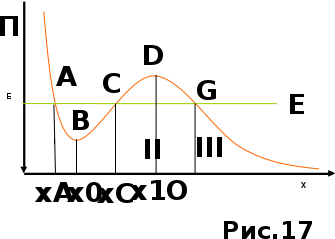
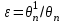 0 < < 1
0 < < 1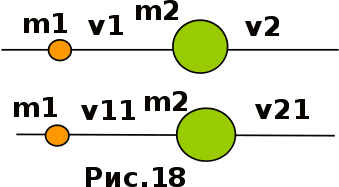 бсолютно упругий удар
бсолютно упругий удар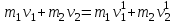 (15.1)
(15.1)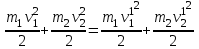 15.2)
15.2)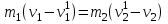 (15.3)
(15.3)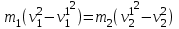 (15.4)
(15.4)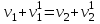 (15.5)
(15.5)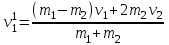 (15.6)
(15.6)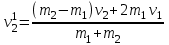 (15.7)
(15.7)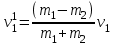 (15.8)
(15.8) 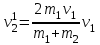 (15.9)
(15.9)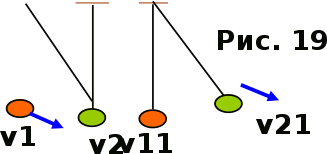
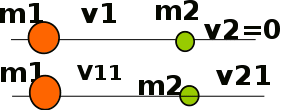
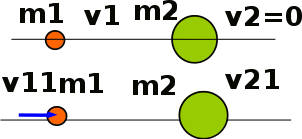
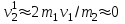




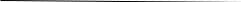

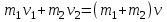
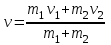
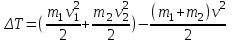
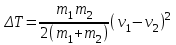
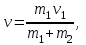
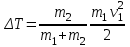
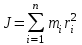 ;
;