Для большинства работников в ЯМ качество изготовленного (приобретенного) коллиматора определяется двумя характеристиками: чувствительность и разрешение. Вообще же описание изготовленного коллиматора требует детальных измерений сложной функции, называемой функцией чувствительности (отклика) для точечного источника (англ. thepointsourceresponsefunction (PSRF)). Эти измерения включают визуализацию точечного источника р/н при разных положениях источника перед фронтальной стороной коллиматора. Диаметр точечного источника при этом должен быть меньше 1 мм.
Геометрическое разрешение коллиматора
PSRFописывает изображение, производимое источником в зависимости от позиции источника и локализации в плоскости изображения. В общем случае позиция источника описывается трехмерным вектором, но учитывая роль плоскости изображения, позиция источника обычно подвергается декомпозиции в двумерный вектор 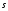 точки в плоскости источника, расположенной на расстоянии z от плоскости изображения. Положение точек на плоскости изображения обозначается вектором точки в плоскости источника, расположенной на расстоянии z от плоскости изображения. Положение точек на плоскости изображения обозначается вектором 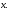 Точка Точка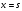 соответствует положению прямо под источником, именно здесь следует ожидать максимума в изображении для КПК. Поэтому вектор соответствует положению прямо под источником, именно здесь следует ожидать максимума в изображении для КПК. Поэтому вектор 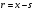 более удобен для определения позиции в плоскости изображения. Функция PSRF выражается в терминах этих векторов в единицах (см-2) следующим образом: более удобен для определения позиции в плоскости изображения. Функция PSRF выражается в терминах этих векторов в единицах (см-2) следующим образом: (4.1) (4.1)
Функция PSRF полностью описывает процесс визуализации и в особенности локальные свойства коллиматора. Однако сравнение PSRF двух коллиматоров затруднительно, так как она зависит от пяти переменных (два двумерных вектора 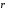 и и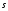 и расстояние z). Для КПК размерность PSRF может быть уменьшена, потому что процесс визуализации инвариантен относительно параллельного перемещения (если не видна структура отверстий). В результате PSRF для КПК не зависит от позиции источника и расстояние z). Для КПК размерность PSRF может быть уменьшена, потому что процесс визуализации инвариантен относительно параллельного перемещения (если не видна структура отверстий). В результате PSRF для КПК не зависит от позиции источника 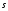 . Остаются три переменных, но при сравнении коллиматоров расстояние F от точечного источника до передней поверхности коллиматора обычно фиксируется на значении, типичном для клинических условий. Следовательно, z = F+T+B является при сравнении коллиматоров постоянной величиной, и зависимость PSRF сокращается до двух переменных. . Остаются три переменных, но при сравнении коллиматоров расстояние F от точечного источника до передней поверхности коллиматора обычно фиксируется на значении, типичном для клинических условий. Следовательно, z = F+T+B является при сравнении коллиматоров постоянной величиной, и зависимость PSRF сокращается до двух переменных.
PSRF является анизотропной по отношению к вектору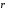 , так как форма отверстия и конфигурация решетки не отвечают азимутальной симметрии. Отсюда дальнейшее уменьшение размерности PSRF при строгом анализе будет некорректным. Однако PSRF зависит от , так как форма отверстия и конфигурация решетки не отвечают азимутальной симметрии. Отсюда дальнейшее уменьшение размерности PSRF при строгом анализе будет некорректным. Однако PSRF зависит от 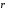 намного сильнее, чем от направления намного сильнее, чем от направления 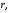 поэтому на практике PSRF часто представляют одномерной функцией, т.е. поэтому на практике PSRF часто представляют одномерной функцией, т.е. 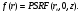 На рис. 4.3 демонстрируется типичная форма этой функции при F = 15 см для одного из коммерческих коллиматоров На рис. 4.3 демонстрируется типичная форма этой функции при F = 15 см для одного из коммерческих коллиматоров
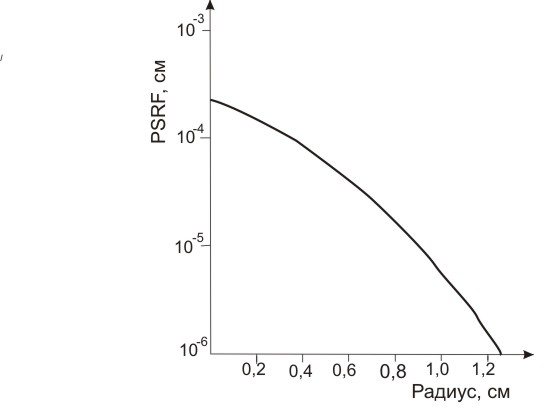
Рис. 4.3. Зависимость PSRF от радиуса r, полученная компьютерным моделированием коммерческого низкоэнергетического универсального коллиматора [1]
Ширина PSRF указывает на предельную способность в определении позиции точечного источника. Сложности возникают по причине двух основных проблем. Первое, ширина PSRF ключевым образом зависит от позиции источника. Например, для КПК ширина PSRF линейно растет с увеличением расстояния до плоскости изображения. Для конвергентного коллиматора разрешение проявляет существенно более сложную зависимость от положения источника.
Ширина на половине высоты (FWHM) PSRF чаще всего используется для характеристики разрешения коллиматора. В принципе, измерение PSRF и определении из нее FWHM связано со сложными экспериментами. К счастью, существует быстрый способ оценки разрешения коллиматора, основанный на его геометрических параметрах. Геометрическое разрешение коллиматора (Rg) опре-деляется как такой радиус 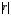 , что при , что при 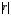 > Rg ни один луч не может пройти через коллиматор, минуя септум. Используя этот простой принцип и подобие треугольников (рис. 4.4), приходим к следующему уравнению: > Rg ни один луч не может пройти через коллиматор, минуя септум. Используя этот простой принцип и подобие треугольников (рис. 4.4), приходим к следующему уравнению:
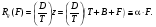 (4.2) (4.2)
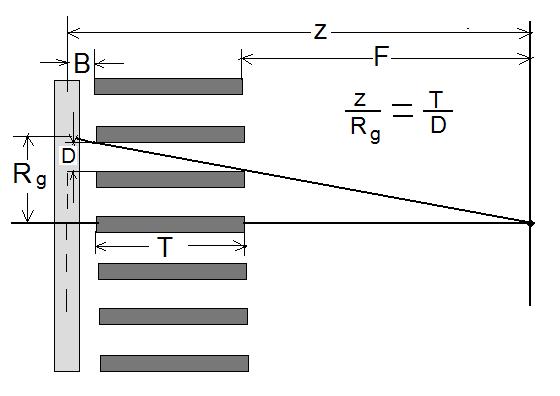
Рис. 4.4. Оценка геометрического разрешения коллиматора (Rg) для точечного источника, расположенного на расстоянии z от плоскости изображения, на основе простых геометрических соотношений, используя подобие треугольников (адаптировано из [1])
Для большинства КПК Rg является неплохой оценкой FWHM 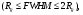 однако точное определение FWHM из PSRF всегда предпочтительней. Обычно B << T<< F, поэтому геомет-рическое разрешение возможно приближенно оценивать как произведение α·R. Дальнейший анализ требует учета специфической формы поперечных сечений каналов. Во многих приложениях адекватным приближением служит гауссовская аппроксимация (GA). В ней предполагается, что PSRF является двумерной функцией Гаусса, центрированной в начале координат с шириной, выбранной так, чтобы значение функции в начале координат равнялось площади поперечного сечения. Для оценки чувствительности и разрешения гауссовская аппроксимация оказывается вполне подходящей. Использование GA приводит к следующему соотношению: однако точное определение FWHM из PSRF всегда предпочтительней. Обычно B << T<< F, поэтому геомет-рическое разрешение возможно приближенно оценивать как произведение α·R. Дальнейший анализ требует учета специфической формы поперечных сечений каналов. Во многих приложениях адекватным приближением служит гауссовская аппроксимация (GA). В ней предполагается, что PSRF является двумерной функцией Гаусса, центрированной в начале координат с шириной, выбранной так, чтобы значение функции в начале координат равнялось площади поперечного сечения. Для оценки чувствительности и разрешения гауссовская аппроксимация оказывается вполне подходящей. Использование GA приводит к следующему соотношению:
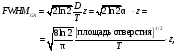 (4.3) (4.3)
которое дает FWHMв терминах геометрии коллиматора, причем опять разрешение определяется отношением α = D/T.
Чувствительность коллиматора
Чувствительность коллиматора, обозначаемая обычно в англоязычной литературе в виде $, определяется как доля испущенных фотонов, которые прошли через коллиматор и достигли плоскости изображения. В общем случае она зависит от положения источника и находится из отношения:

(4.4)
Среднее значение чувствительности, обозначаемое 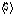 , получается усреднением позиции источника , получается усреднением позиции источника 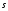 по ячейке решетки КПК выражается в виде по ячейке решетки КПК выражается в виде
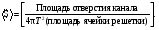 (4.5) (4.5)
В типичном случае средняя чувствительность коллиматора около 3·10-3. Выражение (4.5) ясно демонстрирует масштабирующие свойства КПК коллиматоров, т.е. если все размеры коллиматора умножить на одно и то же число, то величина чувствительности не изменится. Правда, данное свойство пропадает при сильном уменьшении толщины коллиматора, так как это приводит к большому увеличении доли фотонов, проходящих через септу.
Несмотря на подчеркивание, в частности в формуле (4.4), зависимости чувствительности от позиции источника, в оставшейся части раздела $ будет предполагаться постоянной величиной. Действительно для КПК данная зависимость слабая. Объясняется это тем, что вероятность фотону пройти через коллиматор, связано с направлением его эмиссии из источника (при отсутствии рассеяния в пациенте), которое является изотропным.
В аппроксимации чувствительности постоянной величиной имеется три исключения:
источник расположен вне поля коллиматора, тогда чувствительность исчезает совсем. Но если источник отодвинуть на расстояние, большее чем толщина коллиматора (обычно от 2 до 3 см), то многие каналы начнут давать свой вклад в изображение. В результате эффекты конкретных отверстий и септы усредняются;
источник расположен очень близко к коллиматору, тогда чувствительность может сильно зависеть от положения источника. Например, если позиция источника находится прямо против септы, то он будет полностью затенен, если же позиция источника находится на оси канала, то произойдет резкое очерчивание поперечного сечения этого канала;
источник расположен на большом удалении от коллиматора против его центра. Это приводит к очень широкому изображению источника, часть которого может оказаться за полем обзора камеры. Тогда часть отсчетов не будет зарегистрирована и, как следствие, чувствительность упадет. Подобное явление имеет место при расстояниях между источником и коллиматором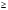 3 м. 3 м.
Таким образом, чувствительность КПК близка к постоянной величине для источников, локализованных в конусообразной области, начинающейся с расстояния 2см и простирающейся до точек на расстоянии
150 см от фронтальной поверхности коллиматора (рис. 4.5).
В случае конвергентных коллиматоров ситуация прямо обратная. Их чувствительность сильно зависит от позиции источника. У таких коллиматоров направления осей каналов зависят от позиции каналов. Чувствительность и коэффициент увеличения изображения источников увеличиваются с приближением точечного источника к фокальной точке. Детальный анализ коллиматоров этих типов проводится в работах [2, 3].
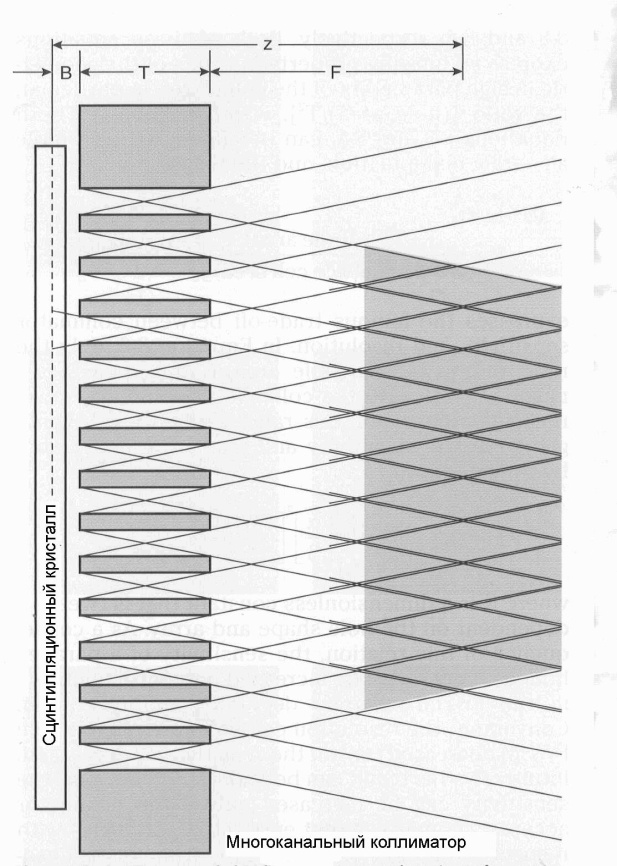
Рис. 4.5. Графическое представление поля обзора и области постоянной чувствительности КПК. Поле обзора каждого канала ограничивается двумя пересекающимися линиями. Область постоянной чувствительности затенена [1]
Компромисс между чувствительностью и разрешением
Разрешение и чувствительность КПК даются формулами (4.3) и (4.5), выражающими визуализационные свойства коллиматора через геометрические параметры. Отметим далее, что член [(площадь отверстия)/T2], входящий в обе формулы, с помощью простых алгебраических преобразований, можно исключить, получив в результате
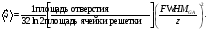 (4.6) (4.6)
Полученное выражение (4.6) и является основой для поиска компромисса между разрешением и чувствительностью КПК. Его можно преобразовать в следующую формулу:
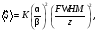 (4.7) (4.7)
где K – безразмерный коэффициент, слабо зависящий от формы отверстий и решетки.
Как видно из (4.7), чувствительность КПК возможно повысить, только увеличив FWHM, тем самым уменьшив разрешение. И наоборот, разрешение можно улучшить, только понизив при этом чувствительность. Большинство производителей коллиматоров понимают это противоречие и выпускают коллиматоры с разным разрешением в зависимости от назначения. В типичном варианте для 99mTc в продаже имеются три низкоэнергетических коллиматора: (высокая чувствительность/низкое разрешение); (высокое разрешение/низкая чувствительность) и (промежуточное разрешение/промежуточная чувствительность) (англ. LEAP). Последний тип коллиматоров называют иногда "универсальный коллиматор".
Проблема видимости схемы расположения отверстий
Даже беглый взгляд на любой коллиматор безусловно выявит структуру отверстий. Устранение этой структуры в изображении является очень важным, так как если расположение отверстий оказывается видимым, то это существенно уменьшает клиническую полезность гамма-камеры из-за очевидных трудностей в анализе распределений РФП. Однако на практике в большинстве клинических приложений сетка коллимационных отверстий в изображении почти не видна. Это не является проявлением специальных свойств коллиматоров, а происходит из-за того, что собственное разрешение детектора гамма-камеры оказывается недостаточным для детектирования отверстий.
"Классический" критерий невидимости координатной сетки отверстий был предложен в работе [4] и имеет вид
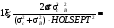 (4.8) (4.8)
где σB – диаметр исследуемого поражения в теле пациента; σс – собственное разрешение гамма-камеры.

Рис. 4.6. Иллюстрация эффекта сетки отверстий каналов для трех коллиматоров при изображении капиллярной трубки диаметром < 1 мм, заполненной 99mTc и размещенной на лицевой стороне коллиматора (F = 0) при различной ориентации относительно структуры отверстий. Изображения (A, B, C, D) создаются коллиматором высокого разрешения для 99mTc (ξ = 0,54); изображения того же источника (E, F, G, H) создаются коллиматором для промежуточных энергий (ξ = 0,052); изображения того же источника (I, J, K, L) создаются 360-кэВ высокоэнергетическим коллиматором (ξ = 0,038) [1]
Число ξ называется параметром конфигурации отверстий коллиматора, и согласно неравенству (4.8) ξ > 1 обеспечивает невидимость структуры дырок в изображении. Небольшие значения ξ (< 0,5) подразумевают, что в изображении могут возникнуть проблемы. Критерий (4.8) можно сформулировать следующим образом: сетка отверстий коллиматора будет невидимой в изображении, если HOLSEP меньше чем и собственное разрешение камеры и визуализируемый объект. Учитывая, что, как правило, размеры исследуемых объектов в ЯМ больше, чем собственное разрешение камеры, то классический критерий выполняется, если HOLSEP <
< σc.
Неравенство (4.8) объясняет, почему сетка отверстий становится проблемой для небольших точечнообразных источников или узких линейных источников. В этих случаях σB < HOLSEP < σс, и критерий нарушается. Этот эффект наглядно демонстрируется на рис. 4.6, где показывается изображение линейного источника (капиллярной трубки) при различной ориентации по отношению сетке отверстий.
Прохождение через септу
Проблема прохождения излучения через септу коллиматоров является важной клинически и трудной в решении. Впервые она была исследована еще в 1957 г. в работе [5], но до сих пор остается актуальной.
В предыдущих разделах различные характеристики коллиматоров оценивались из простого геометрического анализа в предположении немедленного поглощения фотонов после их попадания в септу (материал) коллиматора. Однако ослабление фотонов в средах происходит по экспоненциальному закону, поэтому часть фотонов, падающих на коллиматор, достигает кристалла детектора. При низких энергиях вклад таких фотонов в изображение пренебрежимо мал, но при высоких энергиях (> 200 кэВ) он может представлять серьезную проблему.
Наиболее очевидный эффект, создаваемый такими фотонами, заключается в появлении звездоподобных структур в изображении (рис. 4.7). Этот эффект возникает, потому что фотоны проходят через септу преимущественно по кратчайшим расстояниям, т.е. по направлениям, близким к нормальному падению на фронтальную поверхность коллиматора.
Прохождение фотонов через септу создает, кроме того, диффузный фон в изображении, уменьшая тем самым контрастность изображения.
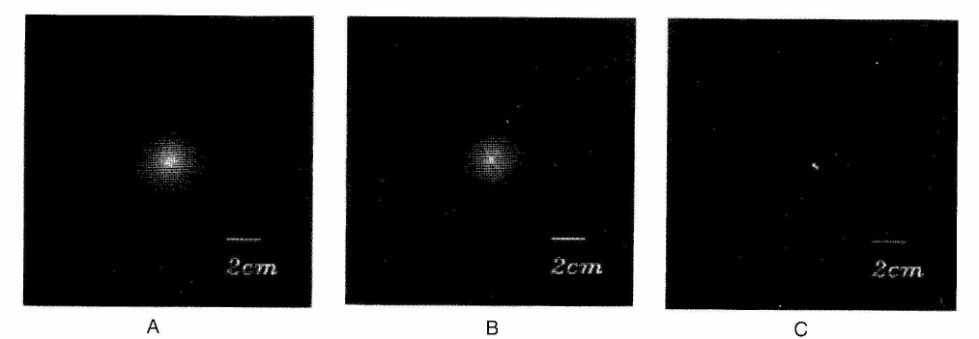
Рис. 4.7. Иллюстрация эффекта влияния на PSRF фотонов, проходящих через материал коллиматора. Три изображения сделаны с точечным (диаметр < 2 мм) высокоэнергетическим источником: А – источник 68Ga (эмиссия позитронов с последующим образованием 511-кэВ фотонов), размещенный на лицевой стороне коллиматора (F = 0) с высоким разрешением для 99mTc; B – источник 131I (основная эмиссия 364-кэВ фотоны) в той же позиции того же коллиматора; С – источник тот же 131I, но высокоэнергетический коллиматор [1]
Точное экспериментальное определение эффекта прохождения является затруднительным. В литературе было предложено несколько способов приближенного определения доли фотонов, прошедших через септу, и продолжительное время велись энергичные споры относительно приемлемого уровня этой доли. В конце концов, согласились, что терпимой является доля, равная 0,05.
В последние два десятилетия ситуация изменилась. Появился ряд компьютерных программ для лучевого анализа траекторий (определение длины пути фотонов в веществе в зависимости от направления их движения и геометрии системы). С помощью этих программ было существенно точнее определено влияние прохождение фотонов через септу на PSRF.
Еще более значимый прогресс в этом направлении был достигнут после разработки программ моделирования прохождения фотонов через коллиматор с помощью метода Монте-Карло. Применение метода Монте-Карло позволило дополнительно оценить также вклад в изображение рассеянного и флуоресцентного излучений. Эти детальные расчеты показали, что суммарное влияние эффектов, связанных с прохождением излучения через септу, рассеянием излучения и образованием флуоресцентного излучения, не так драматично, как предполагали некоторые исследователи. В результате сейчас приемлемой величиной для вклада этих компонентов в суммарный поток излучения, падающего на кристалл, считается значение, равное 0,2.
На основе результатов, полученных в подобных расчетах, в работе [6] была предложена эмпирическая формула для допустимого порога прохождения фотонов через септу. Этот критерий устанавливает, что проектируемый коллиматор будет иметь приемлемый низкий уровень прохождения, если выполняется следующее неравенство:
 (4.9) (4.9)
где P – безразмерная константа (≈ 12), которая зависит от формы отверстия и конфигурации решетки.
Для гексагональных отверстий критерий (4.9) принимает вид
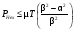 (4.10) (4.10)
|
 Скачать 9.62 Mb.
Скачать 9.62 Mb.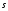 точки в плоскости источника, расположенной на расстоянии z от плоскости изображения. Положение точек на плоскости изображения обозначается вектором
точки в плоскости источника, расположенной на расстоянии z от плоскости изображения. Положение точек на плоскости изображения обозначается вектором 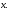 Точка
Точка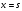 соответствует положению прямо под источником, именно здесь следует ожидать максимума в изображении для КПК. Поэтому вектор
соответствует положению прямо под источником, именно здесь следует ожидать максимума в изображении для КПК. Поэтому вектор 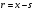 более удобен для определения позиции в плоскости изображения. Функция PSRF выражается в терминах этих векторов в единицах (см-2) следующим образом:
более удобен для определения позиции в плоскости изображения. Функция PSRF выражается в терминах этих векторов в единицах (см-2) следующим образом: (4.1)
(4.1)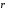 и
и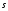 и расстояние z). Для КПК размерность PSRF может быть уменьшена, потому что процесс визуализации инвариантен относительно параллельного перемещения (если не видна структура отверстий). В результате PSRF для КПК не зависит от позиции источника
и расстояние z). Для КПК размерность PSRF может быть уменьшена, потому что процесс визуализации инвариантен относительно параллельного перемещения (если не видна структура отверстий). В результате PSRF для КПК не зависит от позиции источника 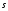 . Остаются три переменных, но при сравнении коллиматоров расстояние F от точечного источника до передней поверхности коллиматора обычно фиксируется на значении, типичном для клинических условий. Следовательно, z = F+T+B является при сравнении коллиматоров постоянной величиной, и зависимость PSRF сокращается до двух переменных.
. Остаются три переменных, но при сравнении коллиматоров расстояние F от точечного источника до передней поверхности коллиматора обычно фиксируется на значении, типичном для клинических условий. Следовательно, z = F+T+B является при сравнении коллиматоров постоянной величиной, и зависимость PSRF сокращается до двух переменных.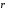 , так как форма отверстия и конфигурация решетки не отвечают азимутальной симметрии. Отсюда дальнейшее уменьшение размерности PSRF при строгом анализе будет некорректным. Однако PSRF зависит от
, так как форма отверстия и конфигурация решетки не отвечают азимутальной симметрии. Отсюда дальнейшее уменьшение размерности PSRF при строгом анализе будет некорректным. Однако PSRF зависит от 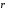 намного сильнее, чем от направления
намного сильнее, чем от направления 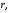 поэтому на практике PSRF часто представляют одномерной функцией, т.е.
поэтому на практике PSRF часто представляют одномерной функцией, т.е. 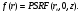 На рис. 4.3 демонстрируется типичная форма этой функции при F = 15 см для одного из коммерческих коллиматоров
На рис. 4.3 демонстрируется типичная форма этой функции при F = 15 см для одного из коммерческих коллиматоров
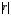 , что при
, что при 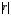 > Rg ни один луч не может пройти через коллиматор, минуя септум. Используя этот простой принцип и подобие треугольников (рис. 4.4), приходим к следующему уравнению:
> Rg ни один луч не может пройти через коллиматор, минуя септум. Используя этот простой принцип и подобие треугольников (рис. 4.4), приходим к следующему уравнению: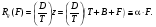 (4.2)
(4.2)
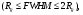 однако точное определение FWHM из PSRF всегда предпочтительней. Обычно B << T<< F, поэтому геомет-рическое разрешение возможно приближенно оценивать как произведение α·R. Дальнейший анализ требует учета специфической формы поперечных сечений каналов. Во многих приложениях адекватным приближением служит гауссовская аппроксимация (GA). В ней предполагается, что PSRF является двумерной функцией Гаусса, центрированной в начале координат с шириной, выбранной так, чтобы значение функции в начале координат равнялось площади поперечного сечения. Для оценки чувствительности и разрешения гауссовская аппроксимация оказывается вполне подходящей. Использование GA приводит к следующему соотношению:
однако точное определение FWHM из PSRF всегда предпочтительней. Обычно B << T<< F, поэтому геомет-рическое разрешение возможно приближенно оценивать как произведение α·R. Дальнейший анализ требует учета специфической формы поперечных сечений каналов. Во многих приложениях адекватным приближением служит гауссовская аппроксимация (GA). В ней предполагается, что PSRF является двумерной функцией Гаусса, центрированной в начале координат с шириной, выбранной так, чтобы значение функции в начале координат равнялось площади поперечного сечения. Для оценки чувствительности и разрешения гауссовская аппроксимация оказывается вполне подходящей. Использование GA приводит к следующему соотношению: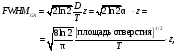 (4.3)
(4.3)
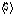 , получается усреднением позиции источника
, получается усреднением позиции источника 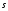 по ячейке решетки КПК выражается в виде
по ячейке решетки КПК выражается в виде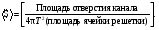 (4.5)
(4.5)
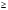 3 м.
3 м.
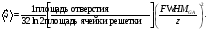 (4.6)
(4.6)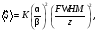 (4.7)
(4.7)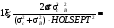 (4.8)
(4.8)

 (4.9)
(4.9)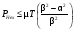 (4.10)
(4.10)