Собственная эффективность
В тех случаях, когда γ-кванты испытывают многократное рассеяние в кристалле, генерируемые X и Y сигналы не точно отражают координаты первичного взаимодействия, так как свет создается в нескольких областях кристалла в пределах временного интервала, меньшего чем временное разрешение ФЭУ. Если существенная доля падающих фотонов испытывает многократное рассеяние, то это может привести к уменьшению пространственного разрешения до неприемлемого уровня. Наиболее эффективный прием борьбы с многократным рассеяниям заключается в уменьшении толщины кристалла, при этом возникает дополнительный положительный эффект, связанный с улучшением энергетического разрешения из-за уменьшения параллакса при распространении света. Но с другой стороны, уменьшение толщины кристалла приводит и к уменьшению собственной эффективности регистрации фотонов.
На рис. 3.7 проводится сравнение эффективностей регистрации фотонов разных энергий для двух толщин кристалла; 12,7 и 6,35 мм. Эта величина определяется как доля γ-квантов, падающих нормально на плоскую поверхность кристалла, которые полностью отдают свою энергию в кристалле либо вследствие фотоэлектрического поглощения, либо в результате многократного комптоновского рассеяния. Как видно из рис. 3.6 для основной γ-линии р/н 131I с энергией 364 кэВ собственная пиковая эффективность для толщины кристалла 12,7 мм равна 0,3, в то время как для 140 кэВ фотонов р/н 99mТс она равна 0,9. Этот пример наглядно демонстрирует, что сочетание гамма-камеры Ангера с генераторами 99mTc явилось важнейшим шагом в развитии инструментария радионуклидной диагностики.
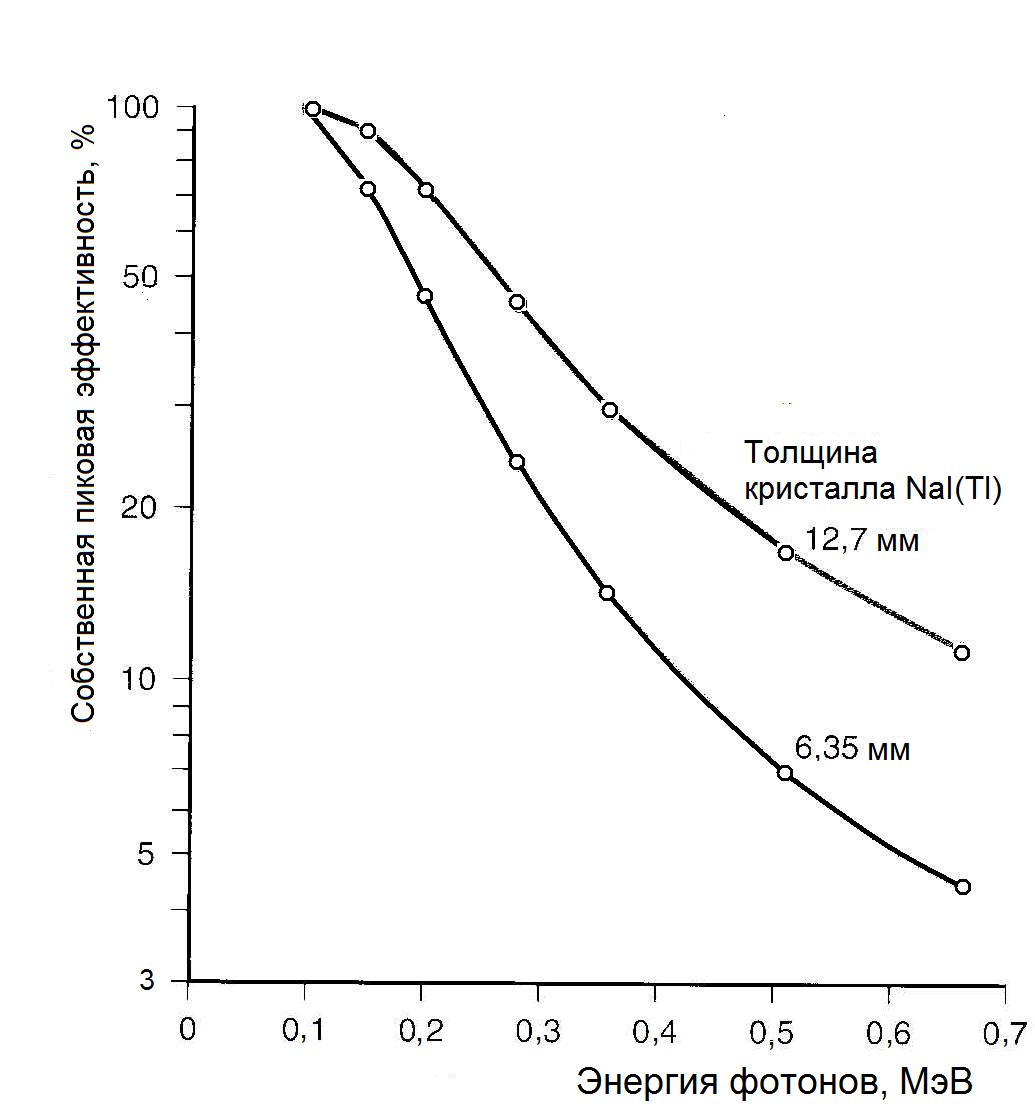
Рис. 3.7. Сравнение зависимости от энергии фотонов собственной пиковой
эффективности кристалла NaI(TL) для двух толщин кристалла
Анализ распределения РФП, испускающих более высокоэнергетичное излучение, чем 99mTc, требует применения кристаллов большей толщины, иначе произойдет уменьшение эффективности регистрации. Увеличение толщины кристаллов в гамма-камере приводит к ряду нежелательных эффектов. Тем не менее, имеются важные приложения (например, регистрация аннигилляционных фотонов с энергией 0,511 МэВ), в которых толщина кристалла повышается до 15 – 25 мм. С возникающими при этом отрицательными эффектами борются с помощью цифрового процессинга.
Эффективность коллиматора
Коллиматор в гамма-камерах прикрепляется непосредственно к лицевой стороне кристалла для ограничения поля видимости, чтобы γ-кванты, образующиеся вне изучаемой области, не могли попасть в детектор. Коллиматоры делаются обычно из материалов с высоким атомным номером высокой тормозной способностью таких, как вольфрам, свинец (наиболее экономичный вариант) и платина. Коллиматоры производятся различного размера, формы и могут включать один или много каналов для просмотра поля интереса.
Классификация коллиматоров чаще всего проводится по типу фокусирования. В зависимости фокусирования они разделяются на коллиматоры: с параллельными отверстиями; каналами, сходящимися в одной точке (конвергентными); каналами, расходящимися из одной точки (дивергентными) и пинхольными (рис. 3.8)
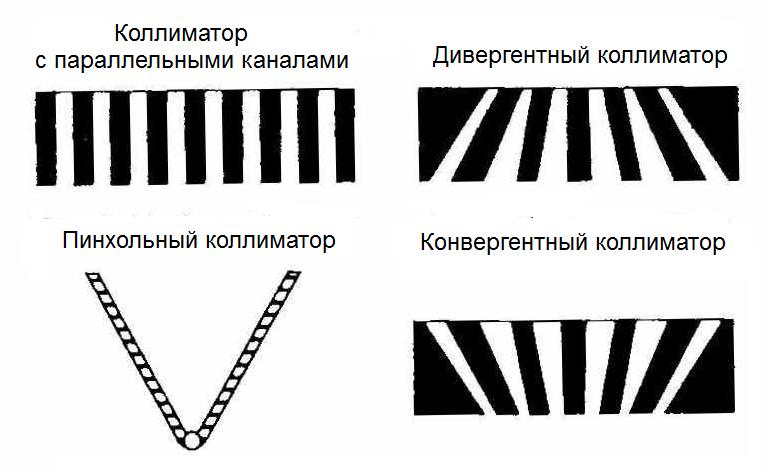
Рис.3.8. Четыре основных типа конструкции коллиматоров для гамма-камер
Пинхольные коллиматоры имеют коническую форму с одним отверстием и применяются для визуализации небольших органов таких, как щитовидная железа, и обеспечивают увеличение изображения. Конвергентные коллиматоры применяются для увеличения изображения, когда орган интереса по размерам меньше размера детектора. Дивергентные коллиматоры, наоборот, применяются, когда размеры органа интереса (например, легкого) шире размеров детектора. Коллиматоры с параллельными отверстиями изготавливаются с большим количеством параллельных каналов (от 4000 до 46000), которые нормальны к поверхности детектора. Они наиболее часто используются в ЯМ и обеспечивают изображение один к одному. Геометрические параметры различных типов коллиматоров показаны на рис. 3.9 и 3.10, расчет геометрических характеристик описывается ниже.
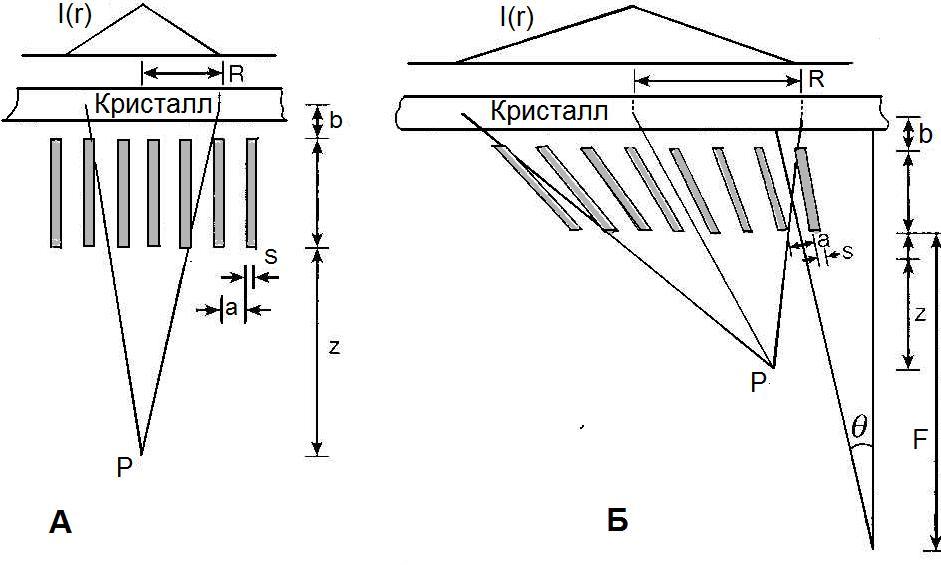
Рис. 3.9. Геометрические параметры коллиматора с параллельными
отверстиями (А) и конвергентного коллиматора (Б)
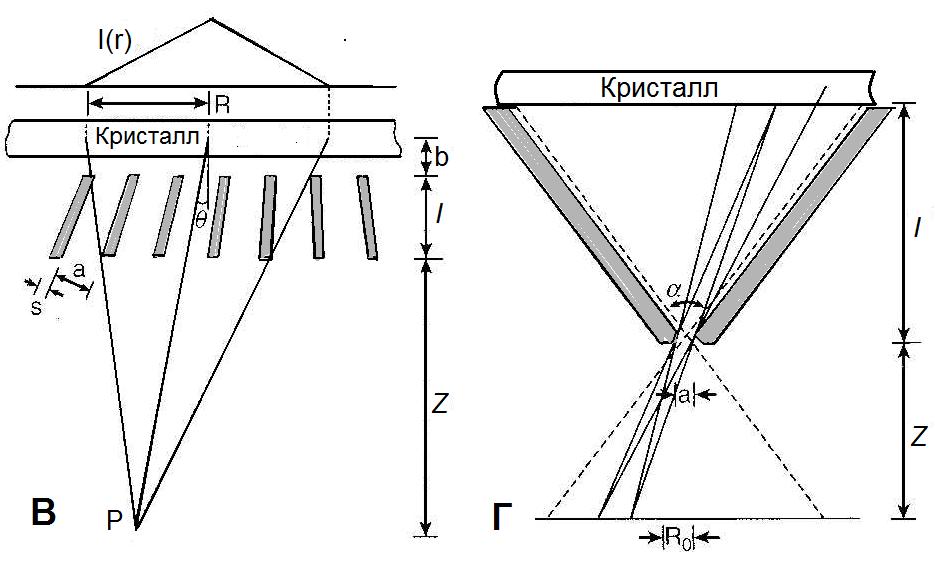
Рис.3.10. Геометрические параметры дивергентного коллиматора (В) и
пинхольного коллиматора (Г)
Расчетные формулы [4] приводятся отдельно для каждого типа коллиматора, при этом используются следующие обозначения: G – геометрическая эффективность для точечного источника; R – ширина распределения на половине высоты; I(r) – плоскость изображения точечного источника, расположенного в точке P; R0 – геометрическое пространственное разрешение в объектной плоскости; le – эффективная длина отверстия (канала); ae– эффективная аппертура; Aopen – площадь одного отверстия на стороне кристалла; Aunit – площадь одного отверстия, включая междуканальный материал вокруг отверстия (например для круглых отверстий Aunit пропорциональна (A + S)2). для других форм отверстий Aopen и Aunit табулированы Ангером. При выводе уравнения для R предполагается однородное параллельное перемещение коллиматора относительно точечного источника P.
Коллиматор с параллельными каналами:
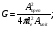 (3.5) (3.5)
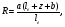 (3.6) (3.6)
где 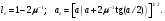
Конвергентный коллиматор:
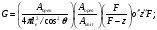 (3.7) (3.7)
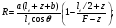 (3.8) (3.8)
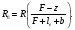 (3.9) (3.9)
Дивергентный коллиматор:
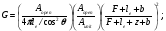 (3.10) (3.10)
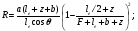 (3.11) (3.11)
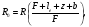 (3.12) (3.12)
где F – расстояние между плоскостью изображения и локальной точкой, расположенной на задней стороне коллиматора.
Пинхольный коллиматор:
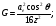 (3.13) (3.13)
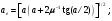 (3.14) (3.14)
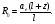 (3.15) (3.15)
Основными параметрами, влияющими на эффективность и разрешение коллиматоров, являются форма и площадь поперечного сечения отверстий, длина каналов и толщина свинца септума ( перегородки) между каналами, которая определяет долю площади кристалла, открытую для излучения. Оптимальная толщина септума зависит от средней длины свободного пробега фотонов и изменяется с энергией.
Коллиматоры с параллельными каналами подразделяются на коллиматоры высокого разрешения, универсальные и высокой чувствительности. Кроме того, существует классификация по энергии: низкоэнергетические, высокоэнергетические и "среднеэнергетические". Высокочувствительные коллиматоры имеют наименьшую толщину, в то время как коллиматоры с высоким разрешением, наоборот, наибольшую.
В настоящее время начали выпускаться "ультра-высоко-энергетические" коллиматоры, предназначенные для регистрации 511-кэВ фотонов. Фирмы предлагают также несколько специальных типов коллиматоров, например, веерные коллиматоры и конусные коллиматоры. У веерных коллиматоров каналы по одной координате являются сходящимися, а по другой параллельными. У конусных коллиматоров каналы сходятся по двум координатам. Оба типа предназначены для увеличения изображений небольших объектов. Наконец, кроме коллиматоров с круглыми сечениями каналов начали производиться коллиматоры с квадратной, гексагональной и даже треугольной формой поперечного сечения. Эти типы коллиматоров обеспечивают более высокое пространственное разрешение, чем коллиматоры с круглыми каналами.
Системная чувствительность
Системная чувствительность характеризует способность гамма-камеры эффективно регистрировать падающие на детектор фотоны. Чувствительность гамма-камеры определяется как число отсчетов, регистрируемых системой в единицу времени, на каждую единицу активности, присутствующей в плоском источнике, расположенным по центру на поверхности коллиматора перпендикулярнок к его оси (с-1·Бк-1). Чувствительность зависит от ряда факторов, в том числе от геометрической эффективности коллиматора, собственной фотоэффективности детектора, установленному уровня дискриминации амплитудного анализатора импульсов (ААИ), мертвому времени системы и др.
При определении чувствительности рекомендуется в зависимости от типа коллиматора использовать жидкие источники 99mTc, 203Hg и 131I в кювете диаметром 100 мм и высотой 3 мм, выбирать энергетическое окно 20 % и скорость счета не более 104 имп./с [3].
-
Пространственное разрешение гамма-камеры определяется как способность прибора верно воспроизводить изображение объекта, четко вырисовывая в результате распределение активности в объекте. Количественно оно может быть определено как наименьшее расстояние между двумя параллельными линейными источниками, при котором на изображении они воспринимаются раздельно. Пространственное разрешение гамма-камеры включает две составляющие: собственную (внутреннюю) и внешнюю, обусловленную, главным образом, коллиматором. Собственное разрешение связано с точностью, с которой взаимодействие может быть локализовано внутри кристалла. Оно измеряется с помощью регистрации трансмиссионного изображения узкощелевого (ширина < 1 мм) фантома и определения распределения отсчетов в направлении, перпендикулярном к длинной оси щели. Кривая результирующего распределения называется функцией расширения (размытия) линии (англ. a line spread function (LSF)), количественно собственное разрешение определяется как полная ширина на половине высоты распределения (англ. full-width-at-half-maximum (FWHM)) (рис. 3.11).
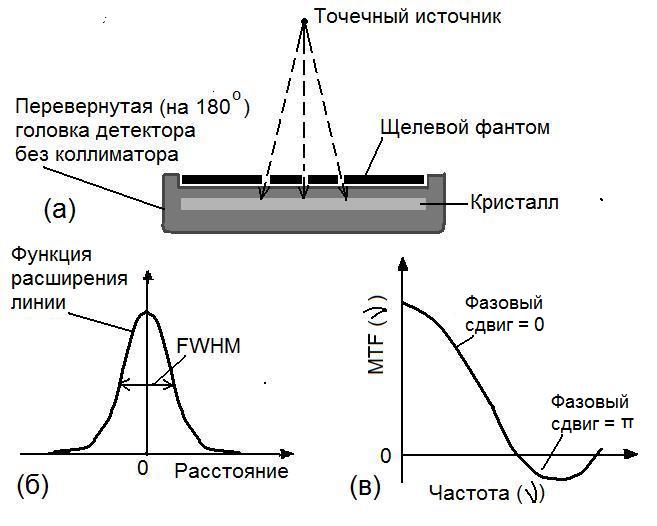
Рис. 3.11. Геометрия измерения внутренней составляющей пространственного разрешения (а), кривая функции расширения (б) и связанная с ней модуляционная функция передачи (в)
Пространственное разрешение всей системы измеряется визуализацией линейного источника с активным диаметром меньшим (< 1 мм), чем ожидаемая величина FWHM. Для этого длинная пластиковая трубка, заполненная радиоактивным раствором, помещается в поле детектора камеры. Гамма-камера, соединенная с компьютером, набирает и запоминает число отсчетов от линейного источника в одном ракурсе, и компьютер генерирует LSF. Отсчеты, полученные на пошаговых расстояниях, вычерчиваются в зависимости от расстояния до центральной оси коллиматора для получения колокообразной кривой LSF (рис. 3.11 и 3.12).
Как видно из рисунка и следует из формул (3.5) – (3.15), форма LSF и разрешение (FWHM) заметно зависят от расстояния источник-коллиматор. В стандартном варианте это расстояние равно 10 см.
Рис. 3.12. Функции расширения линии (LSF) гамма-камеры, снабженной низкоэнергетическим универсальным коллиматором с параллельными каналами, полученные в воздухе (а) и в воде (б) на разных расстояниях от линейного источника 99mTc [5] (Cаша, с. 124)
Следует отметить, что величина FWHM может не представлять истинного пространственного разрешения, так как компоненты, связанные с рассеянием фотонов и прохождением через септум, попадают в хвостовую часть LSF (т.е. ниже 50 %), и поэтому не учитываются.
Более полную и количественную оценку пространственного разрешения прибора дает модуляционная передаточная функция (англ. the modulation transfer function (MTF)). Концепция MTF иллюстрируется на рис. 3.13.
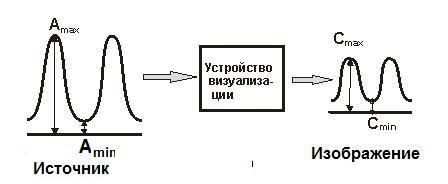
Рис. 3.13. Иллюстрация концепции модуляционной передаточной функции
Пусть распределение активности источника имеет синусоидальный характер с максимальной Amax и минимальной активностями Amin (рис. 3.13). Подобное распределение дает пространственную частоту ν в циклах на сантиметр или в циклах на миллиметр. Контраст или модуляция Msактивности источника равна:
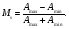 (3.16) (3.16)
В случае идеального устройства визуализации в изображении будут получены такие же Amax и Amin. Однако в реальности амплитуда пика активности будет равна Cmax и минимум активности равен Сmin, меньшие чем Amax и Amin. Тогда модуляция изображения определяется как
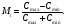 (3.17) (3.17)
Отсюда MTF для пространственной частоты ν рассчитывается по формуле:
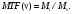 (3.18) (3.18)
Когда Ms = Mi, то MTF = 1 и такой результат получается, если синусоидальные циклы хорошо разделены, а измерительное устройство верно воспроизводит каждый цикл. При сближении пиков и впадин, что соответствует увеличении пространственной частоты распределения, измерительное устройство, в конце концов, перестает их различать. Тогда значение MTF приближается к нулю, что означает наихудшее пространственное разрешение системы. Значения MTF между 0 и 1 представляют промежуточное пространственное разрешение. Важно отметить, что небольшие объекты лучше отображаются при высоких частотах, а широкие объекты при низких частотах.
На практике при анализе пространственного разрешения в зависимости от частоты используется преобразование Фурье нормализованной LSF. Так как Фурье преобразование является комплексной переменной, результат имеет два параметра: амплитуду (модуль) и фазовый угол (угол между комплексным вектором и действительной осью). Первый представляет модуляционную передаточную функцию (см. рис. 3.11). Она, как отмечалось выше, является мерой эффективности передачи относительных амплитуд пространственных частот, содержащихся в распределение объекта.
Графики зависимости MTF от пространственной частоты бывают очень полезны для оценки общего пространственного разрешения системы. Примеры этих зависимостей показаны на рис. 3.14 для трех систем визуализации распределений активности в объекте.
Из рисунка видно, что при очень низких частотах (т.е. широком разделение синусоидальных циклов) MTF практически равны единице для всех трех систем, или, другими словами, все системы дают хорошее отображение источника. При увеличении частоты система A на рис. 3.14 обеспечивает лучшее разрешение, чем система B, а та, в свою очередь, лучшее, чем система С.
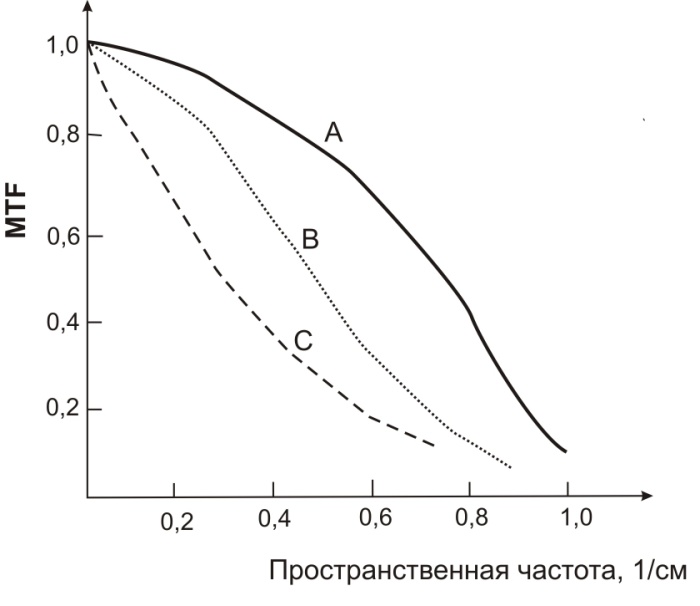
Рис. 3.14. Зависимость MTF от пространственной частоты для трех систем визуализации распределений активности в объекте (Саша. с 126)
Отдельные части системы визуализации могут иметь свои собственные MTF, тогда MTF всей системы получают перемножением индивидуальных MTF:
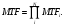 (3.19) (3.19)
Фазовый угол тоже несет важную информацию, так как ненулевое значение фазового угла является признаком пространственного сдвига между объектом и изображением для данной частоты.
Первая камера Ангера имела 19 ФЭУ и внутреннее пространственное разрешение для 140-кэВ фотонов равнялось 10 мм. У современных камер число ФЭУ доходит до 90, а разрешение достигает 3 – 4 мм.
Внутреннее пространственное разрешение улучшается с повышением энергии фотонов и, наоборот, ухудшается с понижением их энергии из-за увеличения статистических флуктуаций при образовании световых фотонов, связанное с уменьшением поглощаемой в кристалле энергии. Оно также улучшается с сужением входного окна амплитудного анализатора, так как при этом уменьшается вклад рассеянного излучения.
Многократное комптоновское рассеяния γ-излучения, сопровождаемое поглощением всех рассеянных фотонов в кристалле, создает неопределенность в X, Y-локализации первичного взаимодействия и ухудшает внутреннее разрешение. Эффект возрастает с увеличением толщины кристалла.
Как отмечалось выше, кроме внутренней составляющей имеется также внешняя (или геометрическая) составляющая пространственного разрешения, связанная с коллиматором. Эту составляющую для четырех типов коллиматоров можно оценить по формулам (3.5) – (3.15). Комбинация обеих составляющих дает величину пространственного разрешения системы Rs:
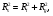 (3.20) (3.20)
где Ri и Rg – внутреннее и геометрическое пространственное разрешение.
Разрешение системы на расстоянии 10 см в рассеивающем материале находится в интервале от 8 до 12 мм в зависимости от разрешения коллиматора. Из уравнений (3.5) – (3.15) следует, что между геометрической эффективностью и пространственным разрешением коллиматоров существует примерно квадратичная зависимость. Этот факт имеет важное практическое значение. Если, например, разрешение двух коллиматоров отличается в два раза, то скорость счета при одинаковых геометрии и источнике будет отличаться уже в четыре раза.
Собственное энергетическое разрешение
Собственное энергетическое разрешение является характеристикой приборной формы линии гамма-камеры и определяет ее способность идентифицировать события, относящиеся к области фотопика (рис. 3.15). Собственное энергетическое разрешение, в основном, связано со свойствами кристалла детектора.
Энергетическое разрешение кристалла NaI(Tl), определяемое как FWHM фотопика, выражается в процентах от энергии γ-кванта. Оно измеряется без коллиматора с помощью точечных источников 99mTc или 57Со (Eγ = 122 кэВ), отнесенных на расстояние не менее пяти диаметров полезного поля изображения. Энергетическое разрешение понижается с уменьшается энергии фотонов, так как FWHM уменьшается медленнее, чем сама энергия. Типичные значения внутреннего энергетического разрешения равны
7 % для 137Cs и
10 % для 99mTc. При измерении разрешения с коллиматором наблюдается небольшое увеличение разрешения в результате эффекта рассеяния излучения на малые углы от стенок коллиматора и образования в свинце коллиматора характеристического 74 кэВ излучения.
Рассеяние в пациенте и коллиматоре
Одна из проблем, возникающих при визуализации распределений низкоэнергетического γ-излучения заключается в трудности отсеивания импульсов от фотонов, рассеянных внутри пациента и в коллиматоре. На рис. 3.15 демонстрируется влияние рассеяния на форму спектра от источника 99mTc.
С уменьшением энергии доля энергии, теряемой фотонами при одном и том же угле комптоновского рассеяния, уменьшается. Так, например, 10 % изменение энергии для 364-кэВ γ-квантов происходит при угле рассеяния
22-градусов, в то время как для 140-кэВ γ-квантов такое относительное изменение энергии соответствует комптоновскому рассеянию на 53-градуса. Отсюда вытекает, что 20 % энергетическое окно (типичное для ядерной визуализации), будет пропускать фотоны, рассеянные на значительно большие углы в случае низкой первичной энергии γ-излучения, чем это имеет место при высоких энергиях. Этот эффект уменьшает разрешение системы, так как местоположение точки рассеяния на такие большие углы неточно описываются пространственными позиционными сигналами.
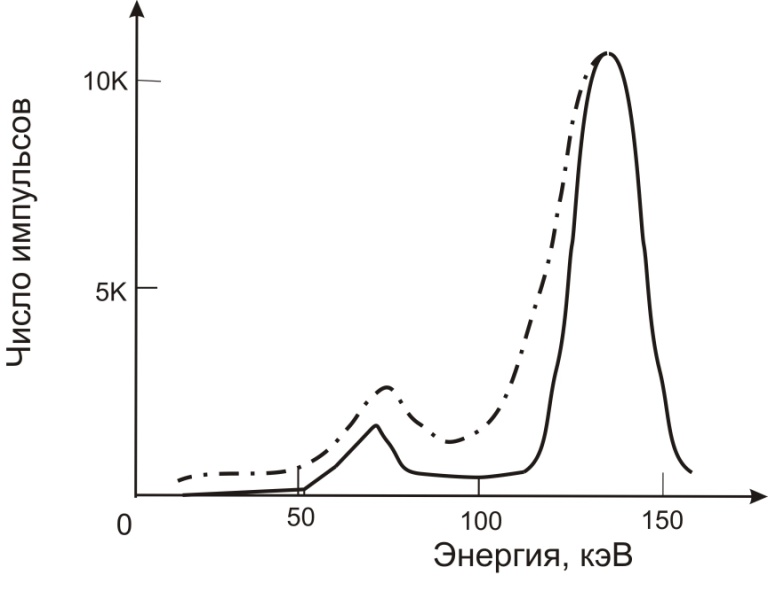
Рис. 3.15. Спектр импульсов от источника 99mTc, измеренный гамма-камерой с низкоэнергетическим коллиматором: ▬▬ – только с коллиматором; ─ ▪ ─ ─ коллиматор плюс плексиглас толщиной 10 см между источником и коллиматором [5]
Устранение импульсов от рассеянных фотонов достаточно затруднительно, так как гамма-камеры традиционно проектируются и настраиваются на работу с симметричными окнами. Произвольное использование асимметричных окон ухудшает однородность чувствительности вдоль поверхности кристалла [6]. Тем не менее, некоторые производители спроектировали гамма-камеры, работающие с асимметричными окнами без потери однородности. Другие пошли по пути разработки компьютерных алгоритмов, которые устраняют селективно импульсы, образованные рассеянными γ-квантами [7].
Пространственная однородность, линейность и энергетическая чувствительность Собственная пространственная однородность
Собственная пространственная однородность (неоднородность) изображения характеризует вариабельность скорости счета гамма-камеры при ее облучении однородным потоком фотонов. Неоднородность изображения – специфические искажения, присущие гамма-камере [3].
Вполне естественно желание иметь у гамма-камер однородный отклик по всему обозреваемому полю. Это означает, что точечный источник независимо от его расположения в поле обзора должен генерировать одинаковую скорость счета в детекторе. Однако даже хорошо отрегулированные и откорректированные гамма-камеры создают неоднородные изображения с вариацией плотности счета не менее 10 %.
Показатель собственной интегральной неоднородности U рассчитывается по формуле [3]:
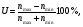 (3.21) (3.21)
где nmax и nmin – соответственно максимальная и минимальная скорость счета по центральному и полезному полю изображения. Полезное поле – круговая площадь с максимальным диаметром, вписываемым в поле обзора коллиматора. Центральное поле – круговая площадь с диаметром, равном 75 % от диаметра полезной площади.
По такой же формуле определяется дифференциальная неоднородность, показывающая максимальное изменение скорости счета в области пяти пикселей во всех строках и столбцах [3].
Неоднородность в чувствительности детектора вызывается несколькими факторами: а) вариацией в откликах ФЭУ; б) нелинейностью в X, Y-позиционировании импульсов в пределах поля обзора; в) краевое "уплотнение" (англ. edgepacking). Лидирующими, с точки зрения, влияния на неоднородность являются два первых фактора.
В ранних системах вариация в откликах ФЭУ уменьшалась последовательной подстройкой их коэффициентов усиления. в настоящее время для этого применяется компьютерное выравнивание с помощью матричных корректирующих факторов, рассчитываемых предварительно [8] и даже on-line [9].
Краевое "уплотнение" проявляется вокруг края изображения как яркий круг и ухудшает тем самым однородность изображения. Причина эффекта заключается в увеличении числа световых фотонов вблизи края детектора за счет процесса отражения от края детектора в направлении фотокатодов ФЭУ. Для борьбы с эти эффектом применяются установка дополнительного свинцового пояса по периферии коллиматора, а в новейших гамма-камерах – электронные средства подавления.
Коррекция энергетической чувствительности
Многочисленные эксперименты однозначно показали, что одной из важных причин пространственной неоднородности является пространственная вариация в энергетическом оклике камеры (вариация в амплитуде импульсов). Если измерить энергетический спектр от коллимированного точечного источника фотонов, падающих на разные участки кристалла гамма-камеры, даже должным образом настроенной, то фотопики не наложатся точно друг на друга. Основной подход к коррекции энергетического отклика заключается в последовательной подстройке энергетического сигнала Z до входа его в амплитудный анализатор импульсов (ААИ).
Сигнал, поступающий в стационарное окно ААИ, находится в интервале Z + ΔΖ, где Z – первоначальная энергия сигнала и ΔΖ – инкремент, добавляемый энергетической коррекцией. Необходимая пространственная вариация ΔΖ находится из матрицы, накладываемой на кристалл. В зависимости от производителя применяются матрицы 64 х 64 и 128 х 128, члены которых определяются предварительно производителями по собственным методикам.
Фирма Сименс, например, разработала схему энергетической коррекции, основанную на принципе идентификации ΔΖ как произведения fZ, где f – доля фактора энергетической коррекции (ΔE/E), рассчитываемая в матрице энергетической коррекции для каждого пикселя из зарегистрированного спектра. Преимущество такого подхода состоит в его применимости к полиэнергетическим окнам. Так как относительная величина энергетической коррекции (f) является независимой от энергии для данного пикселя, то можно рассчитать коррекцию для каждого энергетического импульса, находящегося внутри интервала линейности электроники системы.
Нелинейность и ее коррекция
Коррекция энергетического отклика решает только часть проблемы неоднородности гамма-камеры. Не меньшее влияние на неоднородность имеет погрешность в позиционировании событий. Этот феномен, называемый также нелинейностью гамма-камеры, имеет не случайный характер, а проявляется по определенным предпочтительным направлениям, связанным с особенностями конструкции детектора.
Пространствен6ная нелинейность является систематической погрешностью в позиционировании X-, Y-координат импульсов в изображении и объясняется локальным сжатием или расширением отсчетов. Например, когда источник перемещается в поперечном направлении от края к центру фотокатода ФЭУ, б'ольшая скорость счета наблюдается при его центральном положении, образуя горячее пятно. При приближении источника к краю фотокатода скорость счета, наоборот, уменьшается и образуется холодное пятно.
Геометрические искажения изображения количественно оцениваются показателем собственной пространственной нелинейности, определяемым как абсолютное максимальное отклонение изображение щели маски от прямой линии, выраженное в миллиметрах. Для измерения показателя нелинейности используются маски с линейными или ортогональными отверстиями, которые накладываются на детектор (без коллиматора), а источник излучения размещается на расстоянии не менее пяти диаметров обозреваемого поля. Получающееся изображение запоминается в 128 х 128 матрице (в некоторых моделях 4096 х 4096). Зная действительное положение (X, Y) каждого пикселя и его смещенное X-, Y-положение в изображении, возможно рассчитать матрицу (таблицу) поправочных факторов. На рис. 3.16 представлена диаграмма со специально преувеличенными для наглядности одномерными нелинейностими.
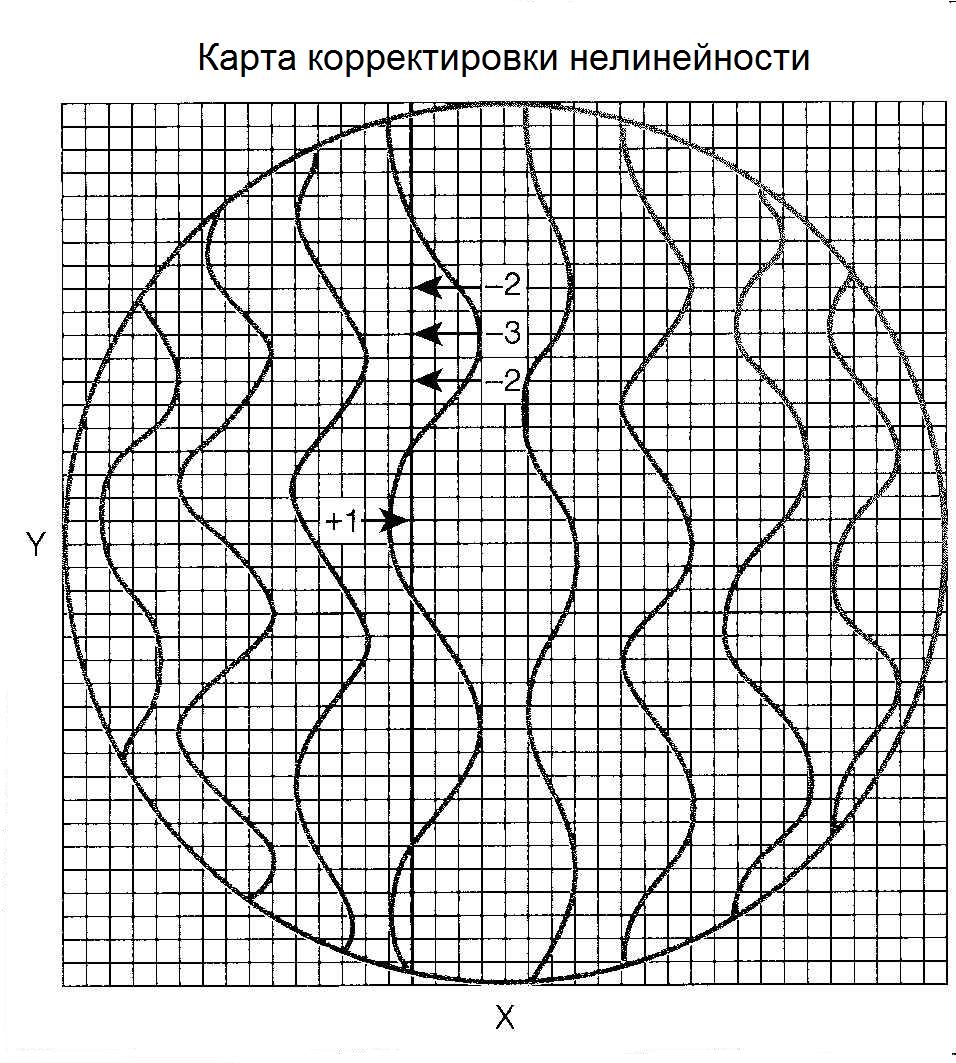
Рис. 3.16. Диаграммное представление преувеличенных нелинейностей в одномерном варианте. Стрелки показывают перемещение сетки изображения в результате корректировки нелинейности [4]
Используя массив поправочных факторов, детектируемые события перемещаются на истинные X-, Y-локализации точек взаимодействия фотонов (в пределах внутреннего разрешения камеры). Для этого в электронную систему современных гамма-камер производители встраивают специальный микропроцессор, в память которого вводятся таблицы с поправочными факторами. Так как обычно гамма-камеры имеют небольшой дрейф характеристик со временем, то эти данные требуется периодически корректировать.
На рис. 3.17 показаны результаты улучшения изображения после введения коррекции энергетического отклика, нелинейности и неоднородности.
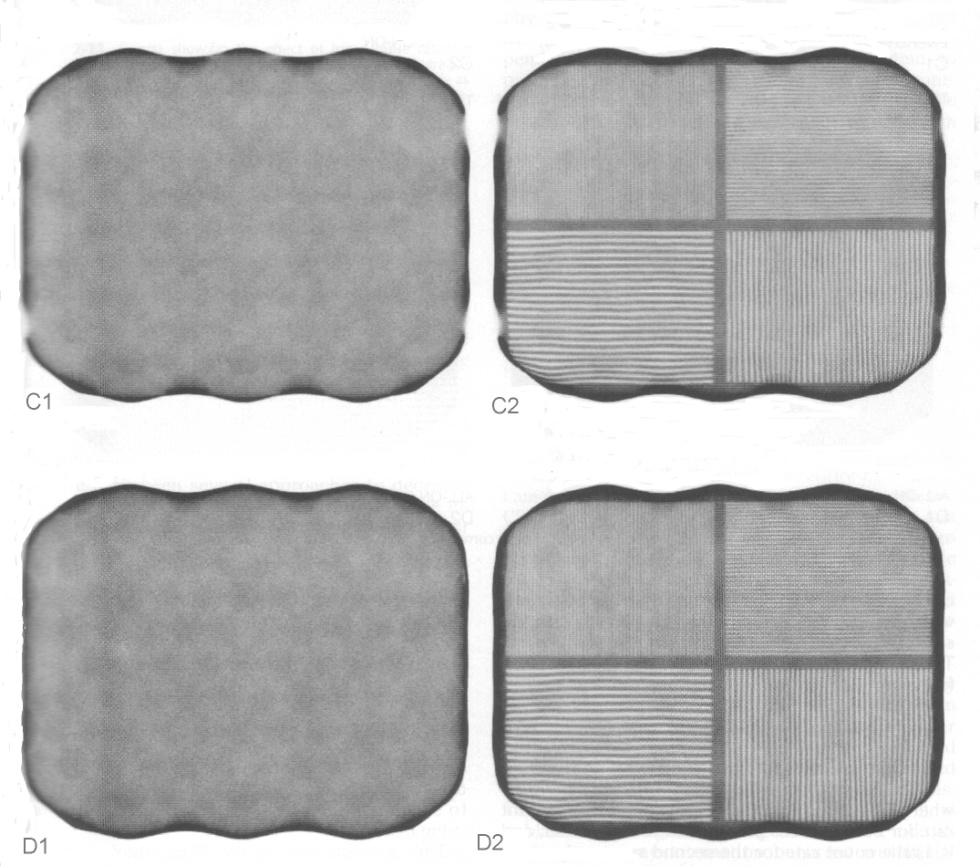
Рис. 3.17. Изображения жидкого источника в кювете (C1, D1) и за четырех секторным щелевым фантомом (C2, D2) без коррекции (С1, С2) и с энергетической корректировкой (D1,D2) [4]

Рис. 3.17 (продолжение). Изображения жидкого источника в кювете (A1, B1) и за четырех секторным щелевым фантомом (A2, B2) c коррекцией энергии и нелинейности(A1, A2) и с коррекцией неоднородности (B1,B2) [4] Автоматическая настройка ФЭУ
Оптимальное функционирование систем, выполняющих on-line коррекцию энергетической чувствительности и нелинейности, возможно только при условии постоянной подстройки ФЭУ. Сегодня фирмы применяют несколько методов для автоматического мониторирования и корректировки коэффициента усиления ФЭУ. Первой такую гамма-камеру выпустила на рынок General Electric. В основе их подхода лежит применение внешних источников света, в качестве которых используются световые диоды, и локализация фотопика в амплитудном спектре от внешнего источника 99mTc. Светодиоды прикрепляются к каждому ФЭУ. Для повышения стабильности их работы применяется температурная стабилизация. Длительность световых импульсов от 1 до 2 мкс. Выходные заряды от ФЭУ, вызываемые световыми вспышками, интегрируются по нескольким световым импульсам и сравниваются с опорным напряжением. Если различие превышает допустимый уровень, то включается автоматическая подстройка коэффициента усиления ФЭУ. Мониторирование осуществляется каждык 10 мс, время подстройки коэффициента усиления 100 мс.
Эффекты высокой скорости счета
Как отмечалось в главе 2, существенным недостатком сцинтилляционных детекторов с кристаллом NaI(Tl) является потеря части импульсов при высокой скорости счета вследствие эффекта наложения импульсов. Наложение импульсов, кроме того, приводит к одновременной регистрации двух событий (на самом деле отстоящих друг от друга на малый временной интервал) как одного события с амплитудой, отличающейся от обоих первичных событий. Если одно или оба события относятся к фотопикам, то тогда амплитуда нового события находится вне заданного интервала окна ААИ и событие будет отброшено, что приведет к потере отсчетов. Если, с другой стороны, "одновременно" регистрируются два фотона, испытавших комптоновское рассеяние, то они могут в сумме создать событие, эквивалентное по амплитуде фотопику, в результате событие будет зарегистрировано а пределах установленного окна ААИ. Но X-, Y- позиции события окажутся в изображении перемещенными куда-то в зону, расположенную между обоими событиями. Это вызывает искажение изображения. Таким образом, чрезмерно высокая скорость счета создает как потери в отсчетах, так и искажение изображения. На рис. 3.18 представлен пример изображения четырех секторного квадратного бар фантома при разных скоростях счета.
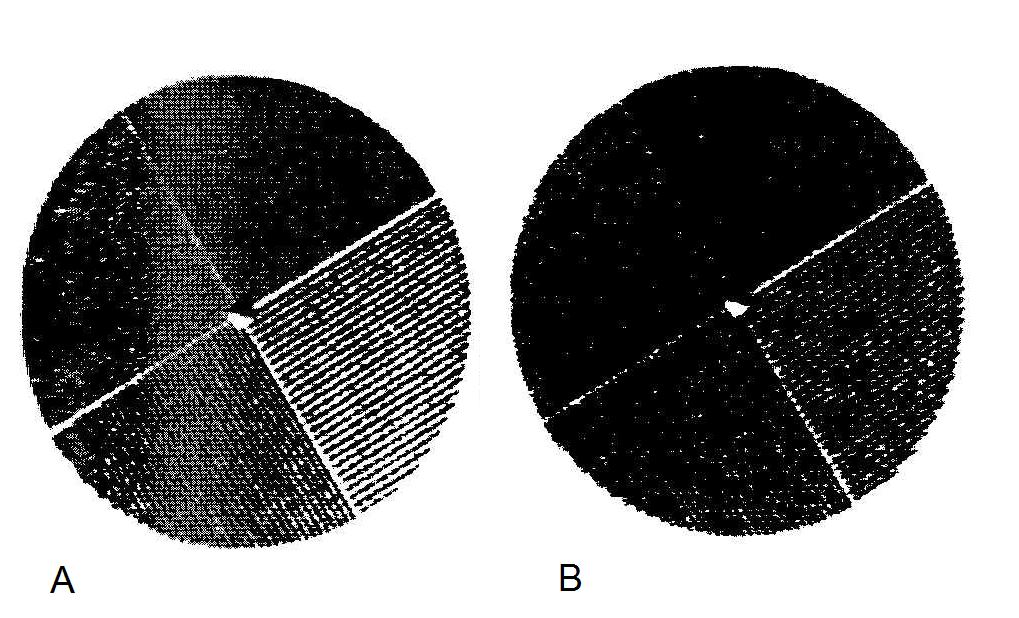
Рис. 3.18. Изображение четырех секторного квадратного бар фантома при разной скорости счета гамма-камеры: A – 10000 c-1; B – 100000 с-1[4] (повторить)
Данная проблема становится особо актуальной для динамических процедур ЯМ. В литературе проводились активные обсуждения по поводу методики измерения мертвого времени гамма-камер, связанные с тем, что сцинтилляционные камеры включают как парализуемые, так и непарализуемые цепи (см. глава 2). Эти системы имеют разные зависимости наблюдаемой скорости счета от скорости поступления входных импульсов (рис. 3.19). В результате обсуждения был одобрен метод расщепленного источника, предложенный Адамсом с коллегами [10]. Если мертвое время найдено, то скорость счета для парализуемой системы рассчитывается по формуле:
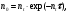 (3.22) (3.22)
где nt – истинная скорость счета (т.е. скорость счета при пренебрежимо малом мертвом времени); n0 – наблюдаемая скорость счета; τ – мертвое время, измеренное методом расщепленного источника.
В этом методе используются два источника 99mTc достаточно высокой активности, чтобы создать скорость счета (0,10/ τ) ± 20 % при размещении их снизу камеры. Сначала измеряется скорость счета от первого источника n1, затем от двух источников, размещенных рядом друг с другом, n12 и, наконец, от одного второго источника n2. Мертвое время парализуемой системы находится из выражения:
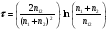 (3.23) (3.23)
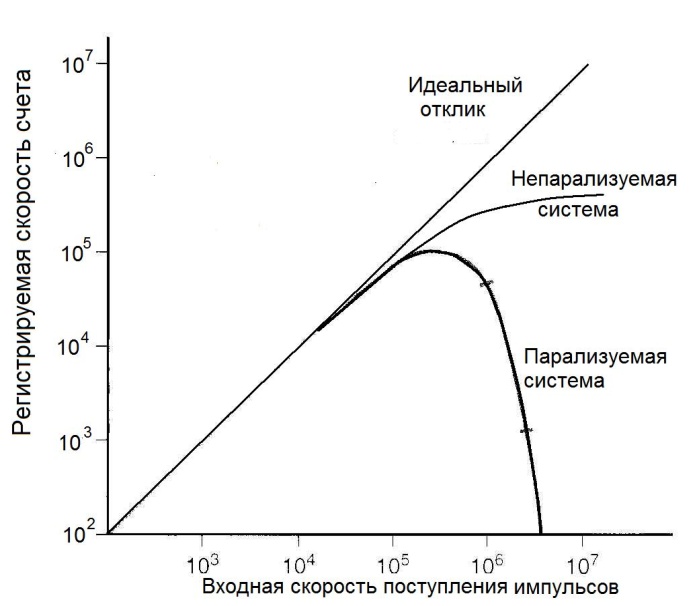
Рис. 3.19. Зависимость регистрируемой скорости счета от входной скорости поступления импульсов для трех разных систем
Результат измерения τ зависит от доли счета в полном энергетическом спектре, которая включается в энергетическое окно, так как компоненты системы, участвующие в измерении мертвого времени, работают перед ААИ. Кроме того, значение мертвого времени зависит также от вклада рассеянного излучения.
В технических данных гамма-камеры обычно указывается наблюдаемая скорость счета для 20 % энергетического окна, при которой из-за мертвого времени теряется 20 % отсчетов. Другой часто специфицируемый параметр представляет скорость счета, при которой зависимость наблюдаемой скорости счета от активности источника приобретает отрицательный наклон. Эта величина является абсолютным пределом для прибора. В современных гамма-камерах эти величины находится в интервале 120000 – 170000 с-1 для 20 % потери счета и 350000 с-1 для абсолютного предела.
Следует упомянуть, что разработчиками было создано несколько вариантов гамма-камер, удовлетворительно работающих при существенно больших загрузках с помощью укорочения длительности импульсов (до 106 с-1, например в [11]). Однако это привело к ухудшению энергетического разрешения. Компания Филипс, разделив детектор на отдельные зоны довела допустимую загрузку до 4·106 с-1, однако данное решение существенно усложнило конструкцию гамма-камеры. Кроме того, эта модель разрабатывалась специально для регистрации аннигиляционных фотонов.
Многокристальные и полупроводниковые гамма-камеры
В предыдущих разделах обсуждались особенности и технические характеристики традиционной гамма-камеры с тонким , но широким кристаллом NaI(Tl), свет от которого регистрировались сборкой ФЭУ. В этом разделе рассмотрим другие конструкции камер, некоторые из которых потенциально являются достаточно перспективными
Многокристальная камера-камера состоит из матрицы индивидуальных γ-детекторов, кристаллов или твердотельных детекторов толщиной от 2 мм до 10 мм, упакованных в единую конструкцию, образующую поле видимости гамма-камеры. Внутреннее разрешение такой системы определяется размерами детекторов. Задача позиционной электроники здесь заключается в простом определении – какой из детекторов активирован? Дополнительным преимуществом такого устройства является возможность работы при высокой скорости счета. Недостаток многокристальной камеры состоит в относительно слабом внутреннем разрешении (> 1 см). В настоящее время коммерческих предложений по ней нет.
Главной особенностью следующей разработки, предложенной в середине 80-х годов прошлого века, является применение позиционно-чувствительного ФЭУ (ПЧФЭУ). Такой ФЭУ имеет площадь фотокатода значительно больше 6 х 6 см2. Принцип его работы иллюстрируется на рис. 3.20.
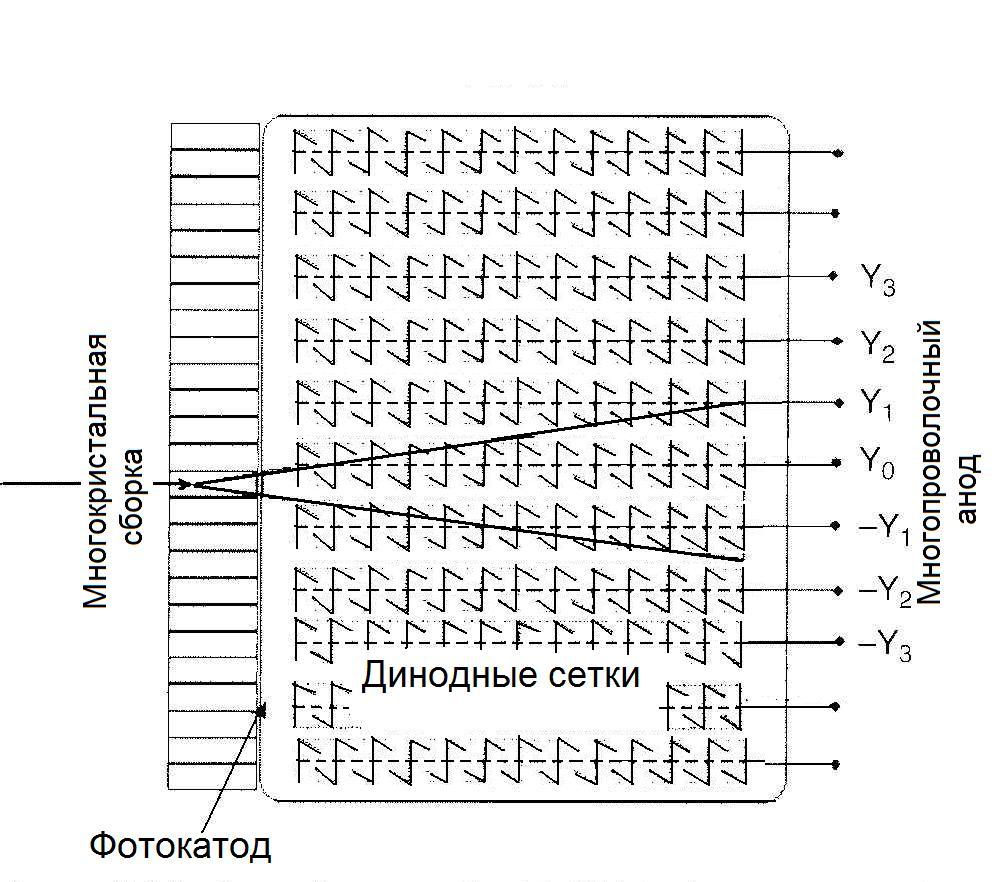
Рис. 3.20. Схематическое изображение позиционно-чувствительного ФЭУ [4]
Внутри ПЧФЭУ расположена двумерная сетка динодов, пространственно организованных так, что они идут от фотокатода к решетке перекрещивающихся анодных проволочек, расположенных на расстоянии 2 – 3 мм друг от друга. Считывание электрического заряда и расчет локализации сцинтилляции света в кристалле подобны таким же операциям в гамма-камере Ангера. Преимущество этой системы в том, что ПЧФЭУ обеспечивает определение локализации события в пределах 2 – 3 мм. Вместе с тем у нее существуют те же проблемы однородности и линейности, как и у гамма-камеры Ангера. Детальное описание одного из вариантов гамма-камеры с ПЧФЭУ и кристаллом CsI(Tl) дается в работе [12]. В настоящее время этот тип гамма-камеры коммерчески доступен.
В следующей новой разработке применено сочетание многокристального детектора и ПЧФЭУ [13,14]. Камера имеет несколько реализаций – от переносного прибора до стационарной камеры с большим поле обзора и предназначена для проведения сцинтимаммографии. Недостатками этого варианта являются большая нелинейность в периферийной области и сильное проявление эффекта мертвого времени. Производство таких камер налажено в нескольких компаниях.
Альтернативой ФЭУ в последнее время успешно выступают полупроводниковые светодиоды (англ. light-sensitivesemiconductorphotodiode (SPD)). Преимущество SPD – малые размеры, что позволяет их монтировать на каждом отдельном кристалле (в многокристальном варианте), относительно большая активная площадь и небольшое "мертвое" пространство. SPD имеют также высокую квантовую эффективность, от 70 до 80 %, по сравнению с 20 % у ФЭУ, однако коэффициент усиления SPDна много порядков меньше чем у ФЭУ. Кроме того, у них высокие токи утечки, поэтому отношение сигнал-шум меньше, чем у ФЭУ, что приводит к худшему энергетическому разрешению. Другой существенный недостаток SPD– сбор электронно-дырочных пар из обедненной носителями зарядов области полупроводника от 2 до 10 раз медленнее, чем распространение электронов через диноды ФЭУ. Следствием является большие потери счета при высокой скорости входных событий.
Несколько групп разработали SPDсистемы гамма-камер [15]. Эти камеры могут рассматриваться как настоящие плоские панели, так как их полная толщина меньше 1 см. Компания Digirad Corporation создала коммерческую систему, состоящую из 4096 кристаллов CsI(Tl) размером 3 х 3 х 6 мм3, сочлененных с матрицей 64 х 64 SPD. Кристаллы CsI(Tl) при работе в паре с SPD, имеют ряд преимуществ перед NaI(Tl), в частности, более походящий к SPDспектр света.
Полупроводники с прямым детектированием излучения (англ. SDR) представляют большой потенциальный интерес для разработчиков гамма-камер с высоким энергетическим разрешением. Германиевые и кремниевые детекторы нашли широкое применение в гамма-спектроскопии. Но их применение в гамма-камерах было затруднительно из-за необходимости охлаждения до температуры жидкого азота. Ситуация изменилась с появлением SDR детекторов на базе диодов с обратно смещенными p-n переходами. Они могут работать при комнатной температуре, но для детектирования γ-излучения с достаточно высокой эффективностью необходима широкая протяженность района, обедненного носителями заряда (именно он является чувствительной областью), высокое напряжение смещения и материал с высокой тормозной способностью. Наиболее подходящим на сегодняшний день является теллурид кадмий цинк (СdZnTe или CZT). Он может работать при комнатной температуре, имеет приемлемое отношение сигнал-шум, энергетическое разрешение от 2 до 5 % . Однако глубина района у CZT, обедненного носителями заряда, порядка 5 мм, что ограничивает его применение, в основном, низкоэнергетическим γ-излучением.
Детекторы CZT сегодня достаточно дорогие, поэтому они применяются в переносных гамма-камерах с небольшим полем обзора. Например, в работе [16] описана переносная CZT гамма-камера с площадью 3,2 х 3,2 см2 с 256 CZT кристаллами размерами 2 х 2 мм2. Разрешение камеры 8,6 % для 140-кэВ фотонов и внешнее пространственное разрешение 2,2 мм FWHM на поверхности низкоэнергетического вольфрамового коллиматора высокого разрешения. В последних моделях энергетическое разрешение для 140-кэВ фотонов улучшено до 6 %.
|
 Скачать 9.62 Mb.
Скачать 9.62 Mb.



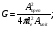 (3.5)
(3.5)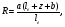 (3.6)
(3.6)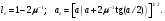
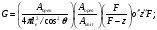 (3.7)
(3.7)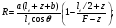 (3.8)
(3.8)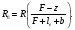 (3.9)
(3.9)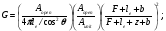 (3.10)
(3.10)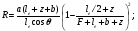 (3.11)
(3.11)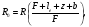 (3.12)
(3.12)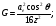 (3.13)
(3.13)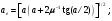 (3.14)
(3.14)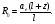 (3.15)
(3.15)

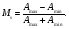 (3.16)
(3.16)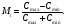 (3.17)
(3.17)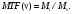 (3.18)
(3.18) 
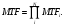 (3.19)
(3.19) 
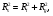 (3.20)
(3.20)
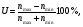 (3.21)
(3.21)



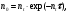 (3.22)
(3.22)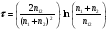 (3.23)
(3.23)
