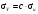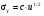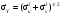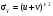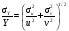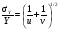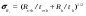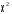Физика ядерной медицины
 Скачать 9.62 Mb. Скачать 9.62 Mb.
|
Статистика регистрации ионизирующих излученийВ предыдущих главах неоднократно подчеркивалось, что радиоактивный распад является по своей природе случайным процессом, поэтому при измерении радиоактивности имеют место флуктуации результатов. Детальное обсуждение статистической обработки результатов измерений находится вне рамок этого пособия. В этом разделе рассматриваются только основные вопросы статистики, связанные с регистрацией излучений в ЯМ. 4.1. Погрешность, точность и воспроизводимостьПри измерении любой величины возможно появление погрешностей (ошибок, англ. errors) или отклонений от истинного значения. Погрешности могут быть двух типов: систематические и случайные. Систематические погрешности проявляются как постоянные отклонения и возникают из-за неисправной работы аппаратуры, неправильной калибровки, несоответствующих экспериментальных условий и т.п.. Эти погрешности можно устранить, исправляя некорректные ситуации. Случайные погрешности являются переменными отклонениями и возникают вследствие флуктуаций в экспериментальных условиях, таких как, например флуктуации высокого напряжения. Но главной их причиной в ЯМ служат законы фундаментальной физики, а именно, статистические флуктуации процесса радиоактивного распада ядер. Точность (правильность, верность, англ. accuracy) измерения величины указывает, насколько близко согласуется результат с истинным значением. Воспроизводимость (разброс, англ. precision) серии измерений (в России эту величину не совсем корректно часто называют погрешностью) описывает повторяемость, воспроизводимость измерения, хотя результаты измерений могут отличаться от среднего значения. Некоторые проблемы в использовании введенных понятий создает тот факт, что в переводе на русский язык accuracy и precision практически синонимы. Чем ближе измерение к средней величине, тем лучше (выше) воспроизводимость, в то время как, чем ближе измерение к истинному значению, тем выше его точность. Подчеркнем, что среднее значение серии измерений, имеющей очень хорошую воспроизводимость, может оказаться далеко от истинного значения. Подобная ситуация иллюстрируется на рис. 2.22. Воспроизводимость может быть улучшена устранением или уменьшением случайных погрешностей, в то время как для повышения точности необходимо уменьшить как случайные, так и систематические погрешности. 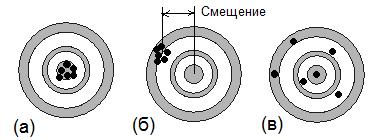 Рис. 2.22. Сравнение точности и воспроизводимости (сходимости): а) хорошая точность и воспроизводимость; б) хорошая воспроизводимость и плохая точность; в) плохая воспроизводимость и плохая точность В ядерной медицине типичное измерение состоит из регистрации (подсчете) событий (отсчетов) в определенном детекторе. Измеряемым параметром является интенсивность источника в единицах отсчетов, детектируемых за определенный интервал времени. В этом случае возможно оценить воспроизводимость измерения из фундаментальных принципов, так как эмиссия и детектирование γ-излучения имеет следующие особенности:
Эти особенности процесса соответствуют распределению вероятности Пуассона (см. далее).
Предположим, что проводится серия измерений некоторой величины в контролируемых условиях. Случайные погрешности измерений проявляются в вариации значений измеряемой величины. Эти отклонения удобно анализировать с помощью частотной гистограммы, представляющей собой график, по оси ординат которого откладывается число измерений с результатами, попадающими в определенный интервал, а по другой значение измеряемой величины (рис. 2.23). При небольшом количестве событий (числе отсчетов), в гистограмме наблюдаются значительные флюктуации, но с увеличением числа событий гистограмма приближается к гладкой кривой. В пределе (число событий стремится к бесконечности) частотная диаграмма полностью раскрывает природу случайных вариаций. 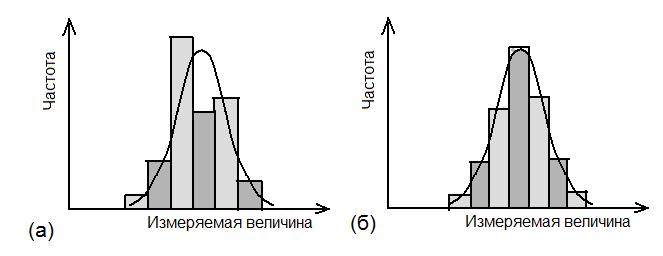 Рис. 2.23. Пример частотных гистограмм при разном количестве измерений: а) недостаточное число измерений; б) большое число измерений Если частотную гистограмму поделить (нормировать) на полное число измерений, то получим распределение вероятности (точнее плотности вероятности), описывающую вероятность при измерении получить конкретное значение исследуемой величины. Наиболее широкое применение находит так называемое нормальное или гауссовское распределение. Оно представляет собой симметричную кривую, характеризующуюся двумя параметрами: средним значением μ, где распределение имеет максимум, и стандартным отклонением σ (σ2 называют дисперсией), характеризующее расширение распределения (рис. 2.24). Математическое выражение распределения Гаусса имеет вид 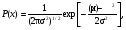 ( 2.19) ( 2.19)где х – непрерывная переменная. Рис. 2.24. Функция распределения Гаусса, имеющая среднее значение переменной x, равное μ, и стандартное отклонение, равное σ. Вероятность получения значений величины в пределах выделенного интервала равняется соответствующей площади под кривой [1](Хенкин, р.9.4, С.128) Если провести случайную выборку из распределения Гаусса (т.е. выполнить серию независимых измерений), то 68 % измеренных величин окажутся в интервале μ ± σ вероятность и 95 % величин попадут в интервал μ ± 2σ. В типичной ситуации μ и σ являются неизвестными параметрами, которые требуется оценить измерений х. Для распределения Гаусса показано, что оптимальный способ оценки μ и σ состоит в расчете арифметического среднего и стандартного отклонения выборки: 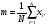 (2.20) (2.20) 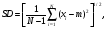 (2.21) (2.21)где xi – результат отдельного измерения; m – среднее значение в серии измерений и оценка μ; SD – стандартное отклонение и оценка σ. В предыдущем разделе при обсуждении статистики отсчетов говорилось, что она описывается распределением Пуассона. Оказывается, что серия отсчетов значений величины может быть аппроксимирован распределением Гаусса, в котором стандартное отклонение равно корню квадратному из среднего значения. Распределение Пуассона описывается следующим выражением: 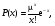 (2.22) (2.22)где x – является целочисленной переменной. Отметим, что распределение Пуассона для своего описания требует только один параметр μ. Стандартное отклонение всегда равно μ1/2. Когда μ становится больше μ > 25, распределение Пуассона практически совпадает с распределением Гаусса, у которого σ = μ1/2 (рис. 2.25). 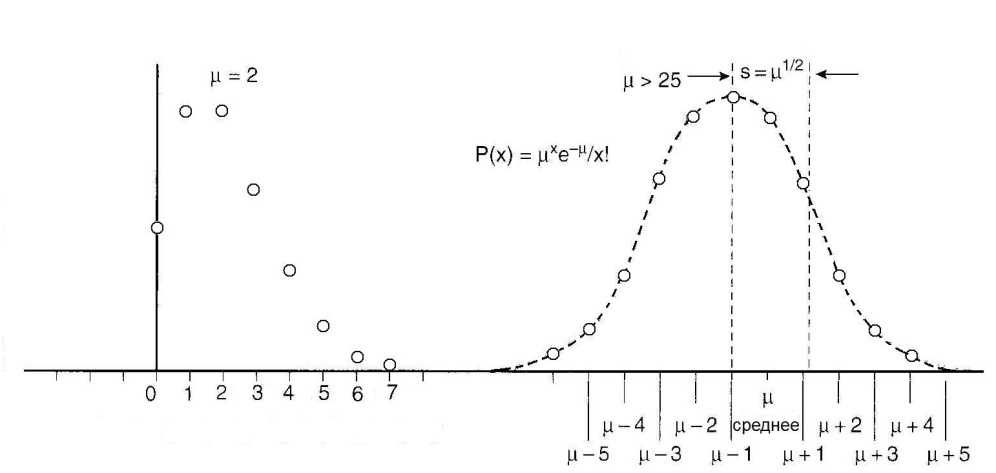 Рис. 2.25. Графическое представление распределения Пуассона. В отличие от распределения Гаусса, которое является непрерывной функцией и позволяет отрицательные значения переменной, распределение Пуассона определено только для положительных значений переменной. Для небольших значений μ распределение Пуассона асимметрично (а) и близко аппроксимируется распределением Гаусса при μ > 25 [1]. Тот факт, что случайная природа измерений скорости счета подчиняется распределению Пуассона, дает определенное преимущество, так как позволяет оценить стандартное отклонение из одного измерения. Так если в результате измерения получено N отсчетов, то в качестве первого приближения N можно считать оценкой среднего значения μ, и отсюда оценкой стандартного отклонения будет SD = N1/2. Стандартное отклонение чаще выражают в относительных единицах, поделив на μ, или в процентах от μ, т.е. помножив еще на 100 процентов (δ(%) = 100 %×SD/ μ). На практике эту величину нередко называют погрешностью (в смысле англ. precision). Вообще говоря, вопросы терминологии в этой области не являются еще четко установившимися и достаточно запутаны. С подачи международных организаций [7] в России традиционный подход, основанный на понятии "погрешность результата измерения" начинает вытесняться подходом, основанном на понятии "неопределенность результата измерения" [8]. Согласно этим рекомендациям неопределенность измерения есть "параметр, связанный с результатом измерения, который характеризует дисперсию значений, которые могли бы быть обоснованно приписаны измеряемой величине" [8]. Преимущество такого подхода заключается в том, что для оценки неопределенности не требуется знания истинного значения измеряемой величины. В этом пособии мы не будем вдаваться в терминологические тонкости, однако понятие неопределенность как оно трактуется в [8], является достаточно удобным для практического использования. Таким образом, относительная погрешность (статистическая) отдельного измерения отсчетов равна 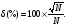 (2.23) (2.23)Из формулы (2.23) хорошо видно, что относительная погрешность уменьшается с увеличением числа отсчетов. Выражение (2.23) нетрудно преобразовать для определения числа отсчетов, обеспечивающих требуемую относительную погрешность: 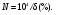 (2.24) (2.24)
При выполнении арифметических операций с переменными, имеющими статистическую погрешность, результат вычислений также будет содержать статистическую погрешность. Величина этой погрешности зависит от вида операции и от погрешностей участвующих в операции переменных. Пусть в операции участвуют две переменные u и v, имеющими неопределенности σu и σv, соответственно. Погрешность результата арифметических операций с этими переменными представлена в табл. 2.2. Для каждой операции неопределенность результата выражена двояко: первый представляет общий случай, правильный для всех типов переменных; второй соответствует случаю, когда u и v являются пуассоновскими переменными, т.е. когда σu = u1/2 и σv = v1/2. Другими словами u и v представляют результат измерения числа отсчетов. Таблица 2.2 Передача погрешностей в арифметических операциях
Учитывая, что многие задачи, встречающиеся в статистике отсчетов, имеют дело со скоростями счета, целесообразно привести сводку полезных формул, относящихся к этой области (табл. 2.3)
Методы статистики позволяют сделать заключения о результатах экспериментов даже при наличии в них случайных погрешностях. Один из часто применяемых статистических методов – это тестирование гипотез. Простейший случай тестирования состоит в выборе из двух альтернатив. Например, требуется решить, являются ли количества отсчетов в двух районах изображения результатом разного усвоения (РФП)? Одна гипотеза предполагает, что плотности отсчетов в этих районах представляют выборки из одного и того же распределения вероятностей. Эту гипотезу называют нулевой гипотезой. Альтернативная гипотеза предполагает, что плотности отсчетов являются выборками из разных распределений. Таблица 2.3 Часто используемые формулы статистики отсчетов
* Rs+b – скорость счета, включая фон; Rb – скорость счета фона; Rs – чистая (без фона) скорость счета; ts+b – полное время измерения источника; tb – время измерения фона. Чтобы решить задачу предположим, что нулевая гипотеза правильная. Тогда может быть вычислена вероятность случайного получения наблюдаемого измеренного значения. Если эта вероятность очень мала, тогда будет оправданно отвергнуть нулевую гипотезу и принять альтернативную. Вероятностный предел отбрасывания нулевой гипотезы называют уровнем значимости и обозначают α. В типичных случаях его значение берут равным 0,05 или 0,01. Так как принятие решения основывается здесь на вероятности, то существует конечная вероятность ошибки. Эти ошибки делятся на два типа. Ошибка I типа имеет место при отбрасывании нулевой гипотезы, когда, на самом деле, она является правильной. Примером такой ошибки будет заключение, что плотности отсчетов, измеренные в разных районах однородного изображения, отражают реальное различие вместо случайной вариации. Минимизировать ошибку I типа можно с помощью выбора подходящего уровня значимости. Ошибка II типа имеет место, когда нулевая гипотеза принимается за истину, в то время, как в действительности, она ложна. Чаще всего такая ошибка совершается при недостаточном количестве надежных данных. Для большей ясности рассмотрим пример. Пусть скорость счета, создаваемая источником А равна 100 отсчетов в секунду, а скорость счета, создаваемая в тех же условиях источником В, равна 110 отсчетов в секунду. Можно ли считать, что оба источника имеют одинаковую активность, если скорости счета измерялись в течение10-секундного временного интервала? В нулевой гипотезе предполагается, что оба источника имеют одинаковую активность, и поэтому разность между измерениями должна иметь распределение со средним значением 0. Используя формулы из табл. 2.2, имеем B –A = (110 – 100) ± (110/10 + 100/10)1/2 =10 ± 4,6. Таким образом, измеренная разность равна 10 со стандартным отклонением 4,6. Так как ожидаемое значение разности есть 0, то 10 представляет 10/4,6 = 2,7 стандартных отклонения. Вероятность получения такого различия, когда А и В имеют одинаковую активность, равна 0,05. Если принято значение уровня значимости α=0,05, то нулевая гипотеза должна быть отвергнута. Однако если принять более жесткий критерий α = 0,01, тогда нулевую гипотезу отбрасывать нельзя. А что произойдет, если время измерения будет равно 39 с? Тогда стандартное отклонение окажется равным (110/36 +100/36)1/2 =2,42. Теперь разность между скоростями счета 10 будет равно 4,1 стандартных отклонений от 0, а вероятность получения такого значения окажется меньше чем 0,01. В такой ситуации можно с высокой степенью точности утверждать, что активности источников А и В различны. Если же время измерения сократить до 1 с, то значение стандартного отклонения окажется равным (100/1 +110/1)1\2 =14,5. В этом случае разность отсчетов 10 находится в пределах одного стандартного отклонения от 0, и нельзя утверждать, что активности источников А и В различны. Подчеркнем, что данный вывод не означает реального равенства активности источников, а является следствием неудачного выбора времени измерения, чтобы доказать обратное.
Вследствие случайной природы радиоактивного распада результаты измерения всегда имеют некоторую неопределенность. Поэтому существует небольшая вероятность того, что значения параметров, оцениваемых из этих измерений, будут равны их истинным значениям. Доверительные уровни определяют интервалы или диапазоны вокруг измеряемой величины, в пределах которой с разумной вероятностью находится истинное значение параметра. Для случайных переменных, имеющих гуссовское распределение вероятностей, доверительные интервалы обычно фиксируются в пределах ±2 (95 %-ая степень доверия) или ±3 (99,7 %-ая степень доверия) стандартных отклонения. Так 95 % доверительные интервалы для разности скоростей счета, рассмотренных в предыдущем разделе, будут следующие: 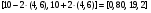 для 10-с измерения; для 10-с измерения;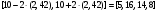 для 36-с измерения; для 36-с измерения;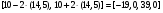 для 1-с измерения. для 1-с измерения.Отметим, что 0 не попадает в 95 %-ный доверительный интервал для 10 и 36 секундных измерений. Это согласуется с отбрасыванием нулевой гипотезы при 0,05 уровне значимости.
Тест хи-квадрат (χ2) является вероятностной статистикой, которая применяется к арифметическим операциям, включающим суммирование квадратов разностей. Выражение для хи-квадрат следующее: 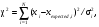 (2.25) (2.25)где xi – i-измеряемая величина; xexpected,i –значение, ожидаемое при каждом измерении на основании некоторой модели; σi– стандартное отклонение при i-измерении. Статистика (критерий) χ2 используется для тестирования гипотез и подгонки кривых. Простой χ2-тест можно применить для определения, являются ли наблюдаемые статистические флуктуации результатов измерений разумными? Или, другими словами, обусловлены ли статистические вариации в ряде измерений статистической случайностью или вариацией других объектов, таких как оборудование, пациент и т.п.? Если проведена серия идентичных измерений числа отсчетов, то χ2 рассчитывается из выражения 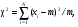 (2.26) (2.26)где m – среднее значение в серии. Так как данные счета имеют пуассоновское распределение, то m является не только оценкой ожидаемого значения случайной величины (количества отсчетов), но также и оценкой σi2. Используя уравнение (2.21), приходим к следующей формуле: 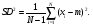 (2.27) (2.27)Преобразуя (2.26) и (2.27), получаем 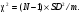 (2.28) (2.28)Если счетчик работает правильно, то следует ожидать, что SD2 будет близко к m. Отсюда получаем, что χ2 должно быть близко к числу измерений (размеру выборки) минус единица (N-1), которую принято называть "число степеней свободы". Вероятность получения различных значений χ2 табулирована в зависимости от числа степеней свободы и в кратком виде приводится в табл. 2.4. Если статистические флуктуации соответствуют ожидаемым значениям, то χ2 будет близко к N-1 и будет иметь вероятность близкую к 0,5. В типовых ситуациях принимаются значения χ2, которые оказываются в диапазоне вероятностей от 0,1 до 0,9. Если вероятность, связанная со значением χ2, оказывается вне данного диапазона, то этот факт служит указанием "что-то неладно со счетчиком". Таблица 2.4 Значения вероятностей для критерия хи-квадрат в зависимости от числа степеней свободы [9]
Рассмотрим пример. Пусть проведена серия из десяти измерений счета от детектора, среднее значение в которых равно 1000 и стандартное отклонение равно 38. Чему равно значение χ2, какова его вероятность P и какое из этого указание? Используя уравнение (2.28), имеем χ2 = (10 – 1) × (38)2/1000 = 12,99. Из табл. 2.4 находим (интерполируя), что вероятность получения величины, большей, чем 12,99 с 9 степенями свободы примерно равна P = 0,2. Так как этот результат попадает в допустимый диапазон, то приходим к выводу, что с детектором все в порядке. Однако 10 измерений являются относительно небольшой выборкой, и ее может оказаться недостаточно для обнаружения неисправности счетчика. Пусть теперь серия состоит из 30 измерений с теми же значениями средней величины и стандартного отклонения. Тогда χ2 = (30 – 1) × (38)2/1000 = 41,9. Из табл. 2.4 находим, что вероятность получения величины, большей, чем 41,9 с 29 степенями свободы P < 0,05. Так как этот результат не попадает в допустимый диапазон, будет разумным сделать вывод о неисправности детектора.
Статистические методы можно применить для просмотра изображений для оценки пределов восприятия. Для примера рассмотрим простое эмиссионное изображение, показанное на рис. 2.26. 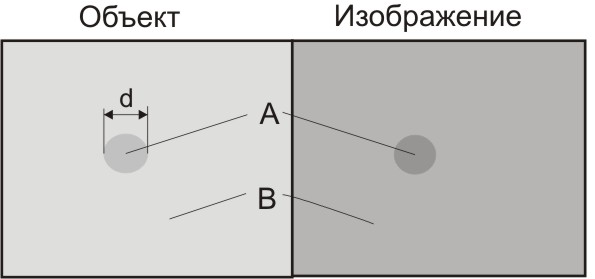 Рис. 2.26. Определение параметров изображения, используя плотность счета в изображении. Контраст: С = |A – B|/A; отношение сигнал-шум: k = |A – B|·d2/(B·d2)1/2 (адаптировано из [10]) Изображение на рис. 2.26 состоит из однородного фона с постоянной плотностью B счет/см2 и области интереса с плотностью счета А счет/см2. Контраст в последней равен С = |A – B|/A. Область А бубудет детектируемой, если счет внутри ее площади существенно отличается от в равной по площади области в окружающем фоне. Так как счет в любом районе имеет статистические флуктуации, разность должна превышать ожидаемое стандартное отклонение, которое равно (B·d2)1/2. Таким образом, требуется, чтобы |(A – B)·d2| > k·(B·d2)1/2. (2.29) где k – коэффициент, представляющий отношение сигнал-шум. Величина k зависит от уровня значимости, необходимого для ограничения ложного вывода, что А и В равны. Обычно требуется, чтобы k > 3. Преобразуем уравнение (2.29), вводя в него контраст C, чтобы получить простое соотношение для определения плотности счета, которая необходима для распознания области размером d при контрасте C: 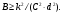 (2.30) (2.30)Для иллюстрации рассмотрим пример. Предположим, что нужно детектировать распознать в изображении область с поперечным размером 2 см и контрастом 0,1 по отношению к фону. Необходимая плотность счета равна 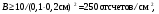 где взято значение k = 3,2 как отношение сигнал-шум. Разумный ли получился результат? В области фона полное число отсчетов 250 отсчетов/см2×4 см2 =1000 отсчетов. Для области с контрастом 0,1 полное число отсчетов будет равно 1000 + 0.1×1000 = =1100. Статистическая неопределенность, связанная с 1000 отсчетов, равна (1000)1/2 = 31,8. Таким образом, 1100 более чем на 3 стандартных отклонения выше фона, или различие с фоном статистически значимо. Отметим, что необходимая плотность счета сильно зависит и от контрастности, и от площади области. Уменьшение одной из этих величин в два раза, требует увеличения плотности счета в четыре раза. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||