Физикотехнический факультет Кафедра теоретической физики и компьютерных технологий курсовая работа реализация игры жизнь на базе технологий java
 Скачать 65.69 Kb. Скачать 65.69 Kb.
|
РЕФЕРАТ Курсовая работа 31 с., 4 источника. КЛЕТОЧНЫЙ АВТОМАТ, КОМБИНАЦИЯ, КОНФИГУРАЦИЯ, ОБЪЕКТНО ОРИЕНТИРОВАННОЕ ПРОГРАММИРОВАНИЕ, КЛАСС, ОБЪЕКТ. Объектами разработки курсовой работы являются объектно-ориентированное программирование на языке Java и использование алгоритма игры «Жизнь». Целью курсовой работы является написание алгоритма игры «Жизнь» на языке Java. В результате выполнения курсовой работы была написана программа реализующая алгоритм игры «Жизнь» математика Конвея с возможностью настройки начальной конфигурации и скорости задержки между шагами симуляции. Содержание Введение Игра жизнь Происхождение игры жизнь Суть игры «Жизнь» Реализация игры «Жизнь» на языке Java Объектно-ориентированное программирование Язык программирования Java Реализация игры «Жизнь» Заключение Список используемых источников Приложение A Приложение Б Введение В 1940 годах многие математики во главе с Джоном фон Нейманом задумывались о создании машины, способной воспроизводить саму себя. После десятилетий попыток и оживленных споров в 1970 впервые была упомянута так называемая игра «Жизнь». Изначально она представляла собой математическую модель, со сложной схемой и сводом правил. В дальнейшем многие программисты пытались воссоздать эту модель на компьютере. Менялись поколения «машин» и технологии программирования – менялась и сама игра, язык на котором она была написана и даже частично правила. На сегодняшний день существуют множество различных версий написания этой игры. Чем же отличается то что делаю я от того что уже было сделано? В своей работе я не пытаюсь «изобрести велосипед». Целью моей работы является написание уже придуманной игры «Жизнь» на объектно-ориентированном языке Java. Предметом моего исследования является сама игра «Жизнь», которая уже более 40 лет привлекает внимание многих ученых и программистов, так что моя работа остается актуальной по сей день. При этом значительно важно решение следующих задач: - Исследование модели игры жизнь, как математической, так и программной - Изучение языка Java - Создание программного кода игры «Жизнь» на языке Java Игра «Жизнь» 1.1 Происхождение игры жизнь В начале в 1940 годах известный математик Джон Конвей заинтересовался проблемой, терзавшей весь математический свет, а именно создание машины, которая смогла бы воспроизводить сама себя. Однако так и не удалось добиться результатов. Через пару лет известный математик Джон фон Нейман, имя которого сегодня связывают с созданием архитектуры большинства современных компьютеров «архитектура фон Неймана», применением теории операторов к квантовой механике (так называемая алгебра фон Неймана), а также один из важнейших участников Манхэттенского проекта, придумал концепцию создания клеточных автоматов. Сама концепция являлась порождением антивиталистической идеологией, то есть возможности создания жизни из мертвой материи. Естественно, нельзя сказать, что идея конечных автоматов перевернула мир, но нашла применение почти во всех отраслях современной науки. «Фон Нейман был блестящим, изобретательным, действенным математиком, с потрясающей широты кругом научных интересов, которые простирались и за пределы математики. Он знал о своём техническом таланте. Его виртуозность в понимании сложнейших рассуждений и интуиция были развиты в высшей степени; и тем не менее, ему было далеко до абсолютной самоуверенности. Возможно, ему казалось, что он не обладает способностью интуитивно предугадывать новые истины на самых высших уровнях или даром к мниморациональному пониманию доказательств и формулировок новых теорем. Мне трудно это понять. Может быть, это объяснялось тем, что пару раз его опередил или даже превзошёл кто-то другой. К примеру, его разочаровало то, что он не первым решил теоремы Гёделя о полноте. Ему это было больше чем под силу, и наедине с самим собой он допускал возможность того, что Гильберт избрал ошибочный ход решения. Другой пример — доказательство Дж. Д. Биркгофом эргодической теоремы. Его доказательство было более убедительным, более интересным и более независимым по сравнению с доказательством Джонни,» - говорил о Неймане Станислав Улам. Сам Станислав Улам работая в Лос-Аламоской национальной лаборатории в те годы изучал рост кристаллов, используя простую решеточную модель. В то же время, Нейман работал над проблемой самовоспроизводящихся систем. Изначально, концепция фон Неймана представляла из себя некоторое подобие робота, собирающего другого робота. Такая модель более известна как кинематическая. Разработав эту модель, фон Нейман осознал сложность создания самовоспроизводящегося робота и, в частности, обеспечения необходимого «запаса частей», из которого должен строиться робот. Улам предложил фон Нейману использовать более абстрактную математическую модель, подобную той, что Улам использовал для изучения роста кристаллов. Таким образом возникла первая клеточно-автоматная система. Подобно решётке Улама, клеточный автомат фон Неймана двухмерный, а самовоспроизводящийся робот описан алгоритмически. Результатом явился универсальный конструктор, работающий «внутри» клеточного автомата с окрестностью, включающей непосредственно прилегающие ячейки, и имеющего 29 состояний. Фон Нейман доказал, что для такой модели существует паттерн, который будет бесконечно копировать самого себя. Также в конце 1940 годов известный американский ученый, выдающийся математик, основоположник кибернетики и теории искусственного интеллекта Норберт Виннер (в будущем удостоенный награды Национальной научной медали США, высшей научной награды в Америке) разработал клеточно-автоматную модель возбудимой среды. Целью было математическое описание распространение импульса в сердечно-нервных узлах. Его оригинальная работа продолжает цитироваться в современных исследованиях до сих пор. В 1960 клеточные автоматы изучались как частный тип динамических систем и впервые была установлена их связь с областью символьной динамики. В связи с чем в 1969 году известный венгерский ученый Г. А. Хедланд провел обзор результатов, полученных в этом направлении. Наиболее значимым результатом явилось описание набора правил клеточного автомата как множества непрерывных эндоморфизмов в сдвиговом пространстве. Наконец, в октябре 1970 года в журнале Scientific American популярный американский математик, писатель, популяризатор науки Мартин Гарднер в рубрике «Математические игры» опубликовал описание игры, написанной известным английским математиком Джоном Хортоном Конвеем и в дальнейшем названной просто «Жизнь». Она использует следующие правила: если клетка имеет двух «живых» соседей, она остаётся в прежнем состоянии. Если клетка имеет трёх «живых» соседей, она переходит в «живое» состояние. В остальных случаях клетка «умирает». Несмотря на свою простоту, система проявляет огромное разнообразие поведения, колеблясь между очевидным хаосом и порядком. Первое русскоязычное упоминание игры «Жизнь» относится к 1971 г. В переводе журнала «Наука и жизнь» она известна как «Эволюция». Таким образом в 1971 году Джон Конвей положил начало многим спорам и философским размышлениям вызываемыми игрой «Жизнь», которые продляться еще не один десяток лет. Суть игры «Жизнь» Чтобы говорить об игре жизнь необходимо знать ее правила: Место действия этой игры – вселенная – это размеченная на клетки поверхность или плоскость – чаще безграничная, но бывает также ограниченные и замкнутые. Конвей взял за основу вселенную не просто так, ведь вселенная - это понятие древнегреческой философии и культуре, представление о природном мире как о пластичном, упорядоченном, гармоническим, целом. Конвей соединил в понятии вселенной две функции – упорядоченную и эстетическую. Каждая клетка на этой поверхности может находиться в двух состояниях: быть «живой» или быть «мёртвой» (пустой). Здесь Конвей поднимает вопрос жизни и смерти. Причем живая может стать мертвой, а мертвая стать живой. Таким образом Конвей с помощью этой модели показывает возможность самовоспроизводимости клеток (с помощью изменения состояния). Каждая клетка имеет 8 соседей. Совокупность 8 клеток на квадратном паркете, имеющих общую вершину с данной клеткой называется окрестность Мура. Окрестность получила свое название в честь известного американского профессора математики и информатики Эдворда Фореста Мура. Окрестность Мура является лишь модифицированной окрестностью фон Неймана, которая брала совокупность 4 вместо 8 клеток на квадратном паркете. Распределение живых клеток в начале игры называется первым поколением. Каждое следующее поколение рассчитывается на основе предыдущего по таким правилам: - в пустой (мёртвой) клетке, рядом с которой ровно три живые клетки, зарождается жизнь; - если у живой клетки есть две или три живые соседки, то эта клетка продолжает жить; в противном случае (если соседей меньше двух или больше трёх) клетка умирает («от одиночества» или «от перенаселённости»); Это наводит на мысль, что все во вселенной развивается по одним и тем же нескольким фундаментальным законам, пока еще не познанных человеком. А рождение и смерть клеток – аналогичный процесс возникновения и исчезновения нейронных импульсов, который и формирует процесс мышления, а также аналогичный созданию импульсов в нервной системе многоклеточных организмов. Игра прекращается, если на поле не останется ни одной «живой» клетки, если при очередном шаге ни одна из клеток не меняет своего состояния (складывается стабильная конфигурация) или если конфигурация на очередном шаге в точности (без сдвигов и поворотов) повторит себя же на одном из более ранних шагов (складывается периодическая конфигурация). Эти простые правила приводят к огромному разнообразию форм, которые могут возникнуть в игре. Игрок не принимает прямого участия в игре, а лишь расставляет или генерирует начальную конфигурацию «живых» клеток, которые затем взаимодействуют согласно правилам уже без его участия (он является наблюдателем). Таким образом игрок берет на себя роль Бога, создавая жизнь в начале и не вмешиваясь в дальнейшее развитие. Вскоре после опубликования правил, было обнаружено несколько интересных шаблонов (вариантов расстановки живых клеток в первом поколении), в частности: r-пентамино и планер (glider). Планер – пятиклеточная конфигурация игры «Жизнь», способная перемещаться в двумерной вселенной с квадратными ячейками. Планер был открыт в 1970 году Ричардом Гаем, когда группа Конвея пыталась отследить развитие R–пентамино. Планер является наименьшим, первым обнаруженным и наиболее часто возникающим космическим кораблём в «Жизни» и перемещается по диагонали со скоростью, равной 1/4 скорости света. Планеры имеют большое значение в «Жизни», поскольку они часто возникают в процессе эволюции, могут образовывать новые конфигурации при столкновении и могут быть использованы для передачи информации на большие расстояния. Целенаправленное построение заданных конфигураций путём столкновения планеров получило название глайдерного синтеза. Блоки, ульи, мигалки, светофоры могут быть получены столкновением всего двух планеров. Требуется 3 планера, чтобы построить космический корабль или пентадекатлон. Конвей первоначально предположил, что никакая начальная комбинация не может привести к неограниченному размножению и предложил премию в 50 долларов тому, кто докажет или опровергнет эту гипотезу. Приз был получен группой из Массачусетского технологического института, придумавшей неподвижную повторяющуюся фигуру, которая периодически создавала движущиеся «планеры». Таким образом, количество живых клеток могло расти неограниченно. Затем были найдены движущиеся фигуры, оставляющие за собой «мусор» из других фигур. К настоящему времени более-менее сложилась следующая классификация фигур: - Планерное ружьё Госпера – первая бесконечно растущая фигура - Устойчивые фигуры: фигуры, которые остаются неизменными - Долгожители: фигуры, которые долго меняются, прежде чем стабилизироваться. - Периодические фигуры: фигуры, у которых состояние повторяется через некоторое число поколений - Двигающиеся фигуры: фигуры, у которых состояние повторяется, но с некоторым смещением - Ружья: фигуры, у которых состояние повторяется, но дополнительно появляется двигающаяся фигура - Паровозы: двигающиеся фигуры, которые оставляют за собой следы в виде устойчивых или периодических фигур - Пожиратели: устойчивые фигуры, которые могут пережить столкновения с некоторыми двигающимися фигурами - Сорняки (паразиты): фигуры, которые при столкновении с некоторыми фигурами дублируются. В дальнейшем было создано множество конфигураций игры жизнь. Одно из самых известных является сад Эдема - конфигурация клеточного автомата, которая не может появиться в результате эволюции, т.е. не имеет родителя. Термин «сад Эдема» был введён Джоном Тьюки ещё в 1950-х годах, задолго до появления «Жизни». Можно попытаться осуществить систематический поиск садов Эдема в порядке возрастания количества клеток, перебирая для каждого кандидата в «сироты» все возможные предшествующие конфигурации. Однако этот метод непрактичен по той причине, что количество конфигураций «Жизни» в прямоугольнике заданной площади N равно 2N, и полный перебор становится неприемлемым даже для умеренных площадей. Более эффективный метод вычислений основан на теории формальных языков; временная сложность этого подхода зависит экспоненциально не от площади, а от ширины ограничивающего прямоугольника. Первый известный сад Эдема в «Жизни», размещающийся в прямоугольнике 9 × 33, был найден Роджером Бэнксом в 1971 году. [1] Две конечные конфигурации клеточного автомата называются близнецами, если их эволюции, начиная со следующего поколения, полностью совпадают. Клеточный автомат называется инъективным, если в этом автомате нет близнецов. Клеточный автомат называется сюръективным в том и только в том случае, если у каждой конфигурации есть родитель, то есть если садов Эдема не существует. Автомат, одновременно являющийся инъективным и сюръективным, называется обратимым клеточным автоматом. Теорема сада Эдема утверждает, что клеточный автомат в евклидовой вселенной является локально инъективным тогда и только тогда, когда он сюръективен. Другими словами, теорема утверждает, что сады Эдема существуют только в тех автоматах, в которых существуют близнецы. Теорема применима к «Жизни», поскольку легко найти две различные конфигурации, которые эволюционируют в следующем поколении в одну и ту же конфигурацию. «Мёртвая вселенная» и одинокая живая клетка в «мёртвой вселенной» эволюционируют в одну и ту же конфигурацию, все клетки которой мёртвые. Следовательно, в «Жизни» существуют сады Эдема. Однако, даже данная конфигурация до сих пор вызывает вопросы. Один из таких вопросов 1983 году задал Мартин Гарднер: «Хотя у любой конфигурации «Жизни» есть лишь один потомок, обратное неверно. У данной конфигурации может быть два или более «отца». Именно поэтому поиск садов Эдема настолько труден: компьютер должен исследовать всех возможных отцов на каждом шаге «в прошлое». <…> Кстати, тот факт, что «сын» сада Эдема может иметь более одного «отца», заставил Конвея предложить приз в 50 долларов первому человеку, который сможет найти конфигурацию, у которой есть «отец», но нет «дедушки». Существование такой конфигурации до сих пор остаётся открытым вопросом.». [1] 2 Реализация игры «Жизнь» на языке Java 2.1 Объектно-ориентированное программирование Используемая в данной работе база технологий Java полностью базируется на объектно-ориентированной модели представления данных. Для того чтобы понять структуру Java, нужно сначала понять, что такое объектно-ориентированное программирование. Объектно-ориентированное, или объектное, программирование - парадигма программирования, в которой основными концепциями являются понятия объектов и классов. Основные понятия объектно-ориентированного программирования: 1 Абстрагирование - это способ выделить набор значимых характеристик объекта, исключая из рассмотрения незначимые. Соответственно, абстракция - это набор всех таких характеристик. 2 Инкапсуляция - это свойство системы, позволяющее объединить данные и методы, работающие с ними, в классе и скрыть детали реализации от пользователя. 3 Наследование - это свойство системы, позволяющее описать новый класс на основе уже существующего с частично или полностью заимствующейся функциональностью. Класс, от которого производится наследование, называется базовым, родительским или суперклассом. Новый класс - потомком, наследником или производным классом. 4 Полиморфизм - это свойство системы использовать объекты с одинаковым интерфейсом без информации о типе и внутренней структуре объекта. 5 Класс является описываемой на языке терминологии (пространства имён) исходного кода моделью ещё не существующей сущности (объекта). Фактически он описывает устройство объекта, являясь своего рода чертежом. Говорят, что объект - это экземпляр класса. При этом в некоторых исполняющих системах класс также может представляться некоторым объектом при выполнении программы посредством динамической идентификации типа данных. Обычно классы разрабатывают таким образом, чтобы их объекты соответствовали объектам предметной области. 6 Объект. Сущность в адресном пространстве вычислительной системы, появляющаяся при создании экземпляра класса или копирования прототипа (например, после запуска результатов компиляции и связывания исходного кода на выполнение). 7 Прототип – это объект-образец, по образу и подобию которого создаются другие объекты. Объекты-копии могут сохранять связь с родительским объектом, автоматически наследуя изменения в прототипе; эта особенность определяется в рамках конкретного языка. В центре ООП находится понятие объекта. Объект - это сущность, которой можно посылать сообщения, и которая может на них реагировать, используя свои данные. Данные объекта скрыты от остальной программы. Сокрытие данных называется инкапсуляцией. Наличие инкапсуляции достаточно для объектности языка программирования, но ещё не означает его объектной ориентированности - для этого требуется наличие наследования. Но даже наличие инкапсуляции и наследования не делает язык программирования в полной мере объектным с точки зрения ООП. Основные преимущества ООП проявляются только в том случае, когда в языке программирования реализован полиморфизм; то есть возможность объектов с одинаковой спецификацией иметь различную реализацию. Особенностью реализации класса является возможность наличия в нем поля данных и методов. Поля данных – это параметры объекта (конечно, не все, а только необходимые в программе), задающие его состояние (свойства объекта предметной области). Иногда поля данных объекта называют свойствами объекта, из-за чего возможна путаница. Физически поля представляют собой значения (переменные, константы), объявленные как принадлежащие классу. Методы – это процедуры и функции, связанные с классом. Они определяют действия, которые можно выполнять над объектом такого типа, и которые сам объект может выполнять. Классы могут наследоваться друг от друга. Класс-потомок получает все поля и методы класса-родителя, но может дополнять их собственными либо переопределять уже имеющиеся. Большинство языков программирования поддерживает только единичное наследование (класс может иметь только один класс-родитель), лишь в некоторых допускается множественное наследование - порождение класса от двух или более классов-родителей. Множественное наследование создаёт целый ряд проблем, как логических, так и чисто реализационных, поэтому в полном объёме его поддержка не распространена. Вместо этого в 1990-е годы появилось и стало активно вводиться в объектно-ориентированные языки понятие интерфейса. Интерфейс - это класс без полей и без реализации, включающий только заголовки методов. Если некий класс наследует (или, как говорят, реализует) интерфейс, он должен реализовать все входящие в него методы. Использование интерфейсов предоставляет относительно дешёвую альтернативу множественному наследованию. Взаимодействие объектов в абсолютном большинстве случаев обеспечивается вызовом ими методов друг друга. Инкапсуляция обеспечивается следующими средствами: - Контроль доступа. Поскольку методы класса могут быть как чисто внутренними, обеспечивающими логику функционирования объекта, так и внешними, с помощью которых взаимодействуют объекты, необходимо обеспечить скрытость первых при доступности извне вторых. Для этого в языки вводятся специальные синтаксические конструкции, явно задающие область видимости каждого члена класса. Традиционно это модификаторы public, protected и private, обозначающие, соответственно, открытые члены класса, члены класса, доступные только из классов-потомков и скрытые, доступные только внутри класса. Конкретная номенклатура модификаторов и их точный смысл различаются в разных языках. - Методы доступа. Поля класса, в общем случае, не должны быть доступны извне, поскольку такой доступ позволил бы произвольным образом менять внутреннее состояние объектов. Поэтому поля обычно объявляются скрытыми (либо язык в принципе не позволяет обращаться к полям класса извне), а для доступа к находящимся в полях данным используются специальные методы, называемые методами доступа. Такие методы либо возвращают значение того или иного поля, либо производят запись в это поле нового значения. При записи метод доступа может проконтролировать допустимость записываемого значения и, при необходимости, произвести другие манипуляции с данными объекта, чтобы они остались корректными (внутренне согласованными). Методы доступа называют ещё аксессорами (от англ. access - доступ), а по отдельности - геттерами (англ. get - чтение) и сеттерами (англ. set - запись). - Свойства объекта. Псевдополя, доступные для чтения и/или записи. Свойства внешне выглядят как поля и используются аналогично доступным полям (с некоторыми исключениями), однако фактически при обращении к ним происходит вызов методов доступа. Таким образом, свойства можно рассматривать как «умные» поля данных, сопровождающие доступ к внутренним данным объекта какими-либо дополнительными действиями (например, когда изменение координаты объекта сопровождается его перерисовкой на новом месте). Свойства, по сути - не более чем синтаксический сахар, поскольку никаких новых возможностей они не добавляют, а лишь скрывают вызов методов доступа. Конкретная языковая реализация свойств может быть разной. Например, в C# объявление свойства непосредственно содержит код методов доступа, который вызывается только при работе со свойствами, то есть не требует отдельных методов доступа, доступных для непосредственного вызова. В Delphi объявление свойства содержит лишь имена методов доступа, которые должны вызываться при обращении к полю. Сами методы доступа представляют собой обычные методы с некоторыми дополнительными требованиями к сигнатуре. Полиморфизм реализуется путём введения в язык правил, согласно которым переменной типа «класс» может быть присвоен объект любого класса-потомка её класса.[2] 2.2 Язык программирования Java Язык программирования Java – это язык, полностью схожий по синтаксису с языком высокого уровня С++, но имеющий ряд отличий. Программы на Java транслируются в байт-код, выполняемый виртуальной машиной Java Virtual Machine— программой, обрабатывающей байтовый код и передающей инструкции оборудованию как интерпретатор. Достоинством подобного способа выполнения программ является полная независимость байт-кода от операционной системы и оборудования, что позволяет выполнять Java-приложения на любом устройстве, для которого существует соответствующая виртуальная машина. Другой важной особенностью технологии Java является гибкая система безопасности, в рамках которой исполнение программы полностью контролируется виртуальной машиной. Любые операции, которые превышают установленные полномочия программы (например, попытка несанкционированного доступа к данным или соединения с другим компьютером), вызывают немедленное прерывание. Часто к недостаткам концепции виртуальной машины относят то, что исполнение байт-кода виртуальной машиной может снижать производительность программ и алгоритмов, реализованных на языке Java. В последнее время был внесен ряд усовершенствований, которые несколько увеличили скорость выполнения программ на Java: применение технологии трансляции байт-кода в машинный код непосредственно во время работы программы (JIT-технология) с возможностью сохранения версий класса в машинном коде; широкое использование платформенно-ориентированного кода (native-код) в стандартных библиотеках; аппаратные средства, обеспечивающие ускоренную обработку байт-кода (например, технология Jazelle, поддерживаемая некоторыми процессорами фирмы ARM).[3] Программы, написанные на Java, имеют репутацию более медленных и занимающих больше оперативной памяти, чем написанные на языке Си. Тем не менее, скорость выполнения программ, написанных на языке Java, была существенно улучшена с выпуском в 1997—1998 годах так называемого JIT-компилятора в версии 1.1 в дополнение к другим особенностям языка для поддержки лучшего анализа кода (такие, как внутренние классы, класс StringBuffer, упрощенные логические вычисления и т. д.). Кроме того, была произведена оптимизация виртуальной машины Java — с 2000 года для этого используется виртуальная машина HotSpot. По состоянию на февраль 2012 года, код Java 7 приблизительно в 1.8 раза медленнее кода, написанного на языке Си. [3] Идеи, заложенные в концепцию и различные реализации среды виртуальной машины Java, вдохновили множество энтузиастов на расширение перечня языков, которые могли бы быть использованы для создания программ, исполняемых на виртуальной машине. Эти идеи нашли также выражение в спецификации общеязыковой инфраструктуры CLI, заложенной в основу платформы .NET компанией Microsoft. Основные возможности Java: автоматическое управление памятью. расширенные возможности обработки исключительных ситуаций. набор стандартных коллекций: массив, список, стек и т. п. наличие простых средств создания сетевых приложений (в том числе с использованием протокола RMI). наличие классов, позволяющих выполнять HTTP-запросы и обрабатывать ответы. встроенные в язык средства создания многопоточных приложений, которые потом были портированы на многие языки. В Java методы, не объявленные явно как static, final или private, являются виртуальными в терминологии C++: при вызове метода, по-разному определённого в базовом и наследующем классах, всегда производится проверка времени выполнения. Абстрактным методом (модификатор abstract) в Java называется метод, для которого заданы параметры и тип возвращаемого значения, но не тело. Абстрактный метод определяется в классах-наследниках. В C++ то же самое называется чисто виртуальной функцией. Для того чтобы в классе можно было описывать абстрактные методы, сам класс тоже должен быть описан как абстрактный. Объекты абстрактного класса создавать нельзя. Высшей степенью абстрактности в Java является интерфейс (interface). Все методы интерфейса абстрактны: описатель abstract даже не требуется. Интерфейс в Java не считается классом, хотя, по сути, является полностью абстрактным классом. Класс может наследовать/расширять (extends) другой класс или реализовывать (implements) интерфейс. Кроме того, интерфейс может наследовать/расширять другой интерфейс. В Java класс не может наследовать более одного класса, зато может реализовывать сколько угодно интерфейсов. Множественное наследование интерфейсов не запрещено, то есть один интерфейс может наследоваться от нескольких. Интерфейсы можно передавать методам как параметры, но нельзя создавать экземпляры интерфейсов. В языке Java имеются только динамически создаваемые объекты. Причём переменные объектного типа и объекты в Java — совершенно разные сущности. Переменные объектного типа являются ссылками, то есть неявными указателями на динамически создаваемые объекты. Это подчёркивается синтаксисом описания переменных. При присваиваниях, передаче в подпрограммы и сравнениях объектные переменные ведут себя как указатели, то есть присваиваются, копируются и сравниваются адреса объектов. А при доступе с помощью объектной переменной к полям данных или методам объекта не требуется никаких специальных операций разыменовывания — этот доступ осуществляется так, как если бы объектная переменная была самим объектом. Объектными являются переменные любого типа, кроме примитивного. Явных указателей в Java нет. В отличие от указателей C, C++ и других языков программирования, ссылки в Java в высокой степени безопасны благодаря жёстким ограничениям на их использование, в частности: Нельзя преобразовывать объект типа int или любого другого примитивного типа в указатель или ссылку и наоборот. Над ссылками запрещено выполнять операции ++, −−, +, − или любые другие арифметические операции. Преобразование типов между ссылками жёстко регламентировано. За исключением ссылок на массивы, разрешено преобразовывать ссылки только между наследуемым типом и его наследником, причём преобразование наследуемого типа в наследующий должно быть явно задано и во время выполнения производится проверка его осмысленности. Преобразования ссылок на массивы разрешены лишь тогда, когда разрешены преобразования их базовых типов, а также нет конфликтов размерности. В Java нет операций взятия адреса (&) или взятия объекта по адресу (*). Благодаря таким специально введенным ограничениям в Java невозможно прямое манипулирование памятью на уровне физических адресов. [4] 2.3 Реализация игры «Жизнь» Из расчета правил, лежащие в основе игры «Жизнь» был создан класс, содержащий главную логику программы, класс LifeModel. Сама модель данных игры «Жизнь» представляет собой поле точек, завернутых в тороид, т.е. все стороны которого являются замкнутыми. Это сделано для того, чтобы ограничить создание большого поля для бесконечного движения движущихся фигур. При симуляции используется принцип двойной буферизации. Двойная буферизация —это метод подготовки данных, обеспечивающий возможность отдачи готового результата, без прерывания процесса подготовки следующего результата. При использовании двойной буферизации вывод информации осуществляется во вторичный буфер, а чтение информации для отдачи «наружу» — из первичного. Первичным буфером является массив mainField, вторичным – массив backField. В массивах хранятся значения 0, если клетка является мертвой, и 1, если клетка является живой. Каждое новое поколение клеток сменяет старое за один шаг симуляции. За каждый шаг отвечает метод simulate(), проходящий все точки и меняющий их в зависимости от условий игры «Жизнь». Если у какой-либо живой точки оказывается меньше 2 или больше 3 соседей она «умирает», если же у мертвой клетки оказывается 3 соседа, она снова начинает жить. Как только из условий сформируется следующая конфигурация, она помещается во вторичный массив. В конце симуляции содержимое массивов mainField и backField меняется для вывода информации о новой конфигурации на экран и обработки следующего поколения. Для управления программой и задания начальной конфигурации реализован класс LifePanel. Управление происходит с помощью компьютерной мыши. Левой кнопкой мыши на поле ставится живая клетка, правой кнопкой она убирается. Задержка (в миллисекундах) между симуляциями регулируется с помощью специального ползунка, расположенный к верху от основного поля (Приложение Б). Весь код используемый в программе представлен в приложении А. Таким образом, используя объектно-ориентированный язык программирования Java была реализована игра «Жизнь», созданная Конвеем. ЗАКЛЮЧЕНИЕ Основные результаты курсовой работы состоят в следующем: Было рассмотрено происхождение алгоритма математической модели, разработанной Джоном Конвеем и названной впоследствии игрой «Жизнь». Были выявлены правила происхождения новых конфигураций и некоторые их типы. Рассмотрен объектно-ориентированный язык программирования Java использующийся при написании программы. Написан код программы, реализующий алгоритм математической модели игры «Жизнь» на базе технологий Java. СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ 1 Грэхем Иан. Объектно-ориентированные методы. Принципы и практика. - 3-е изд. - М.: «Вильямс», 2004 2 Zakhour, S: The Java Tutorial: A Short Course on the Basics, 4th Edition 2006 3 Синтес Антони. Освой самостоятельно объектно-ориентированное программирование за 21 день. - М.: «Вильямс», 2002 4 Эккель Брюс: Thinking in Java 2, Prentice Hall, 2000 ПРИЛОЖЕНИЕ А package swing.life; import java.awt.BorderLayout; import java.awt.Color; import java.awt.Dimension; import java.awt.Graphics; import java.awt.Insets; import java.awt.event.ActionEvent; import java.awt.event.ActionListener; import java.awt.event.MouseAdapter; import java.awt.event.MouseEvent; import java.util.Arrays; import javax.swing.JButton; import javax.swing.JFrame; import javax.swing.JLabel; import javax.swing.JPanel; import javax.swing.JSlider; import javax.swing.JToolBar; import javax.swing.SwingUtilities; import javax.swing.UIManager; import javax.swing.event.ChangeEvent; import javax.swing.event.ChangeListener; class LifeModel { private byte[] mainField = null; private byte[] backField = null; private int width, height; private int[] neighborOffsets = null; private int[][] neighborXYOffsets = null; /** * Инициализация модели. * * @param width * ширина поля данных * @param height * высота поля данных */ public LifeModel(int width, int height) { this.width = width; this.height = height; mainField = new byte[width * height]; backField = new byte[width * height]; neighborOffsets = new int[] { -width - 1, -width, -width + 1, -1, 1, width - 1, width, width + 1 }; neighborXYOffsets = new int[][] { { -1, -1 }, { 0, -1 }, { 1, -1 }, { -1, 0 }, { 1, 0 }, { -1, 1 }, { 0, 1 }, { 1, 1 } }; } public int getWidth() { return width; } public int getHeight() { return height; } public void clear() { Arrays.fill(mainField, (byte) 0); } public void setCell(int x, int y, byte c) { mainField[y * width + x] = c; } public byte getCell(int x, int y) { return mainField[y * width + x]; } /** * Один шаг симуляции. */ public void simulate() { // обрабатываем клетки, не касающиеся краев поля for (int y = 1; y < height - 1; y++) { for (int x = 1; x < width - 1; x++) { int j = y * width + x; byte n = countNeighbors(j); backField[j] = simulateCell(mainField[j], n); } } // обрабатываем граничные клетки // верхняя и нижняя строки for (int x = 0; x < width; x++) { int j = width * (height - 1); byte n = countBorderNeighbors(x, 0); backField[x] = simulateCell(mainField[x], n); n = countBorderNeighbors(x, height - 1); backField[x + j] = simulateCell(mainField[x + j], n); } // крайние левый и правый столбцы for (int y = 1; y < height - 1; y++) { int j = width * y; byte n = countBorderNeighbors(0, y); backField[j] = simulateCell(mainField[j], n); n = countBorderNeighbors(width - 1, y); backField[j + width - 1] = simulateCell(mainField[j + width - 1], n); } // обмениваем поля местами byte[] t = mainField; mainField = backField; backField = t; } /** * Подсчет соседей для не касающихся краев клеток. * * @param j * смещение клетки в массиве * @return кол-во соседей */ private byte countNeighbors(int j) { byte n = 0; for (int i = 0; i < 8; i++) { n += mainField[j + neighborOffsets[i]]; } return n; } /** * Подсчет соседей для граничных клеток. * * @param x * @param y * @return кол-во соседей */ private byte countBorderNeighbors(int x, int y) { byte n = 0; for (int i = 0; i < 8; i++) { int bx = (x + neighborXYOffsets[i][0] + width) % width; int by = (y + neighborXYOffsets[i][1] + height) % height; n += mainField[by * width + bx]; } return n; } /** * Симуляция для одной клетки. * * @param self * собственное состояние клетки: 0/1 * @param neighbors * кол-во соседей * @return новое состояние клетки: 0/1 */ private byte simulateCell(byte self, byte neighbors) { return (byte) (self == 0 ? (neighbors == 3 ? 1 : 0) : neighbors == 2 || neighbors == 3 ? 1 : 0); } } class LifePanel extends JPanel implements Runnable { private static final long serialVersionUID = -7705111475296001684L; private Thread simThread = null; private LifeModel life = null; /** * Задержка в мс между шагами симуляции. */ private int updateDelay = 100; /** * Размер клетки на экране. */ private int cellSize = 8; /** * Промежуток между клетками. */ private int cellGap = 1; /** * Цвет мертвой клетки. */ private static final Color c0 = new Color(0x505050); /** * Цвет живой клетки. */ private static final Color c1 = new Color(0xFFFFFF); public LifePanel() { setBackground(Color.BLACK); // редактор поля MouseAdapter ma = new MouseAdapter() { private boolean pressedLeft = false; // нажата левая кнопка мыши private boolean pressedRight = false; // нажата правая кнопка мыши @Override public void mouseDragged(MouseEvent e) { setCell(e); } @Override public void mousePressed(MouseEvent e) { if (e.getButton() == MouseEvent.BUTTON1) { pressedLeft = true; pressedRight = false; setCell(e); } else if (e.getButton() == MouseEvent.BUTTON3) { pressedLeft = false; pressedRight = true; setCell(e); } } @Override public void mouseReleased(MouseEvent e) { if (e.getButton() == MouseEvent.BUTTON1) { pressedLeft = false; } else if (e.getButton() == MouseEvent.BUTTON3) { pressedRight = false; } } /** * Устанавливает/стирает клетку. * * @param e */ private void setCell(MouseEvent e) { if (life != null) { synchronized (life) { // рассчитываем координаты клетки, на которую указывает // курсор мыши int x = e.getX() / (cellSize + cellGap); int y = e.getY() / (cellSize + cellGap); if (x >= 0 && y >= 0 && x < life.getWidth() && y < life.getHeight()) { if (pressedLeft == true) { life.setCell(x, y, (byte) 1); repaint(); } if (pressedRight == true) { life.setCell(x, y, (byte) 0); repaint(); } } } } } }; addMouseListener(ma); addMouseMotionListener(ma); } public LifeModel getLifeModel() { return life; } public void initialize(int width, int height) { life = new LifeModel(width, height); } public void setUpdateDelay(int updateDelay) { this.updateDelay = updateDelay; } /** * Запуск симуляции. */ public void startSimulation() { if (simThread == null) { simThread = new Thread(this); simThread.start(); } } /** * Остановка симуляции. */ public void stopSimulation() { simThread = null; } public boolean isSimulating() { return simThread != null; } @Override public void run() { repaint(); while (simThread != null) { try { Thread.sleep(updateDelay); } catch (InterruptedException e) { } // синхронизация используется для того, чтобы метод paintComponent // не выводил на экран // содержимое поля, которое в данный момент меняется synchronized (life) { life.simulate(); } repaint(); } repaint(); } /* * Возвращает размер панели с учетом размера поля и клеток. */ @Override public Dimension getPreferredSize() { if (life != null) { Insets b = getInsets(); return new Dimension((cellSize + cellGap) * life.getWidth() + cellGap + b.left + b.right, (cellSize + cellGap) * life.getHeight() + cellGap + b.top + b.bottom); } else return new Dimension(100, 100); } /* * Прорисовка содержимого панели. */ @Override protected void paintComponent(Graphics g) { if (life != null) { synchronized (life) { super.paintComponent(g); Insets b = getInsets(); for (int y = 0; y < life.getHeight(); y++) { for (int x = 0; x < life.getWidth(); x++) { byte c = life.getCell(x, y); g.setColor(c == 1 ? c1 : c0); g.fillRect(b.left + cellGap + x * (cellSize + cellGap), b.top + cellGap + y * (cellSize + cellGap), cellSize, cellSize); } } } } } } public class LifeSim extends JFrame { private static final long serialVersionUID = 3400265056061021539L; private LifePanel lifePanel = null; private JButton button1 = null; private JButton button2 = null; private JSlider slider = null; public LifeSim(String title) { super(title); setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); setResizable(false); lifePanel = new LifePanel(); // размеры поля lifePanel.initialize(100, 70); add(lifePanel); JToolBar toolBar = new JToolBar(); toolBar.setFloatable(false); add(toolBar, BorderLayout.NORTH); button1 = new JButton("Запустить"); toolBar.add(button1); button2 = new JButton("Очистить поле"); toolBar.add(button2); // бегунок, регулирующий скорость симуляции (задержка в мс между шагами // симуляции) slider = new JSlider(1, 200); slider.setValue(50); lifePanel.setUpdateDelay(slider.getValue()); slider.addChangeListener(new ChangeListener() { @Override public void stateChanged(ChangeEvent e) { lifePanel.setUpdateDelay(slider.getValue()); } }); toolBar.addSeparator(); toolBar.add(new JLabel(" Быстро")); toolBar.add(slider); toolBar.add(new JLabel("Медленно")); // запуск/остановка симуляции; попутно меняется надпись на кнопке button1.addActionListener(new ActionListener() { @Override public void actionPerformed(ActionEvent e) { if (lifePanel.isSimulating()) { lifePanel.stopSimulation(); button1.setText("Запустить"); } else { lifePanel.startSimulation(); button1.setText("Остановить"); } } }); // очистка поля button2.addActionListener(new ActionListener() { @Override public void actionPerformed(ActionEvent e) { synchronized (lifePanel.getLifeModel()) { lifePanel.getLifeModel().clear(); lifePanel.repaint(); } } }); button1.setMaximumSize(new Dimension(100, 50)); button2.setMaximumSize(new Dimension(100, 50)); slider.setMaximumSize(new Dimension(300, 50)); pack(); setVisible(true); } public static void main(String... args) { try { UIManager.setLookAndFeel(UIManager.getSystemLookAndFeelClassName()); } catch (Exception e) { } SwingUtilities.invokeLater(new Runnable() { public void run() { new LifeSim("LifeSim"); } }); } ПРИЛОЖЕНИЕ Б 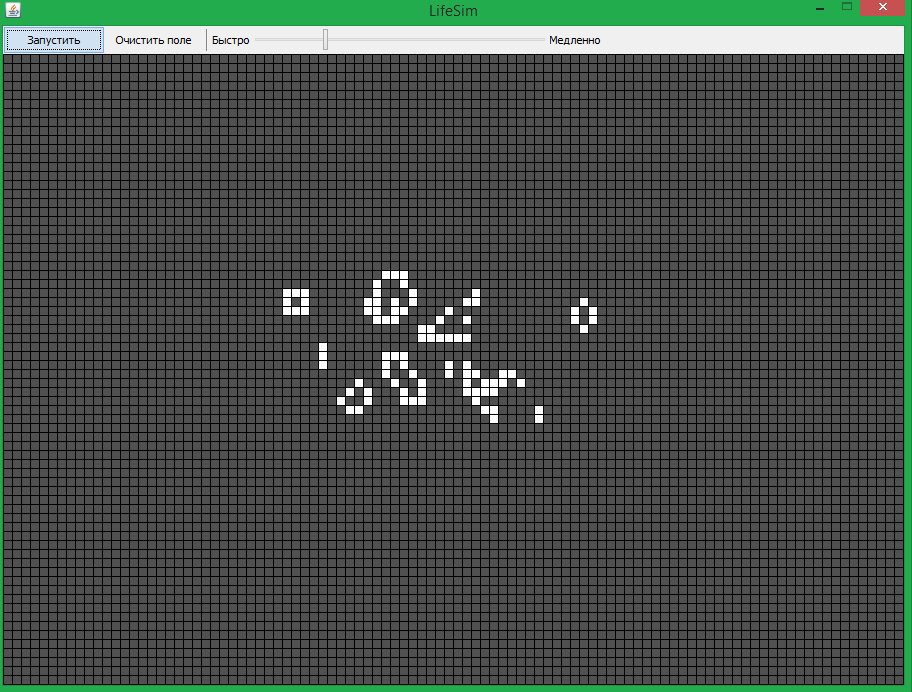 Рисунок 1 – Главное окно приложения. | |||||||||
