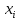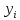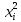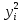Практическая работа Эконометрика. Форма обучения очнозаочная выполнение практических заданий по дисциплине
 Скачать 53.43 Kb. Скачать 53.43 Kb.
|
|
Автономная некоммерческая организация высшего образования МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ Кафедра экономики и управления Форма обучения: очно-заочная ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ «Эконометрика» Группа 21Э371в Студент Т. Н. Белецкая МОСКВА 2023 ЗАДАНИЕ ПО ПРАКТИЧЕСКОЙ РАБОТЕ 1.Укажите основные этапы эконометрического исследования. Ответ: 1.Постановочный этап включает в себя постановку цели исследования и набора экономических переменных. 2.Априорный этап выявляет сущность экономического показателя, а также формирование и формализацию априорной(известной до начала моделирования) информации. 3.На информационном этапе производится регистрация значений, участвующих в модели факторов и показателей. 4.На этапе спецификации модели (подробного описания объекта исследования) обнаруженные связи и соотношения выражаются в математической форме; устанавливается список экономических переменных и взаимосвязи экзогенных и эндогенных переменных, в том числе лаговых; производится формулировка исходных предпосылок и ограничений модели. 5.Этап параметризации модели характеризуется выбором общего вида модели и выявлением входящих в нее связей. 6.На этапе идентификации модели проводится статистический анализ модели, дается оценка ее параметров при помощи статистических методов(например, регрессионного анализа). 7.Этап верификации модели предполагает проверку адекватности модели и точности расчетов. 2.Назовите виды аналитических зависимостей, наиболее часто используются при построении моделей. Ответ: При построении эконометрических моделей могут использоваться различные виды аналитических зависимостей. Наиболее часто используются следующие виды зависимостей: Линейная y = a+ 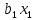 + +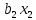 …+ …+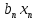 +𝜀 +𝜀 Степенная y = a 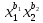 … …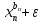 Полулогарифмическая y = a+ 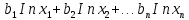 +𝜀 +𝜀Гиперболическая y = a+ 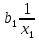 + +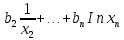 +𝜀 +𝜀Экспоненциальная y = 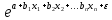 Может применяться также комбинация представленных выше зависимостей. y = a+ 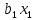 + +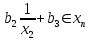 +𝜀 +𝜀При выборе аналитической зависимости учитывают требования простоты модели и возможности наглядной экономической интерпретации ее параметров. Исходя из этих соображений, наиболее часто для представления эконометрической модели используются линейная и степенная функции. 3.Охарактеризуйте функции, которые чаще всего используются для построения уравнения парной регрессии. Ответ: Функция парной регрессии может быть как линейной, так и нелинейной. Линейная регрессия – это выраженная в виде прямой зависимость среднего значения какой-либо величины от некоторой другой величины. В модели линейной парной регрессии зависимость между переменными в генеральной совокупности представляется в виде: где у – зависимая переменная; х – независимая переменная; α и β - параметры уравнения (параметр α – свободный член регрессии; параметр β – коэффициент регрессии, который измеряет, на сколько единиц в среднем изменится результативный признак при изменении фактора на одну единицу; ε – случайная ошибка. К видам нелинейной парной регрессии относятся функции: 1. Степенная функция 2. Функция экспоненты 3. Показательная функция 4. Функция равносторонней гиперболы 5. Обратная функция: Степенная функция нелинейной парной регрессии имеет вид: y = 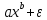 Функция экспоненты нелинейной парной регрессии имеет вид: y = 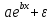 Показательная функция нелинейной парной регрессии имеет вид: y = 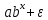 Функция равносторонней гиперболы нелинейной парной регрессии имеет вид: y =a+ 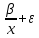 Обратная функция нелинейной парной регрессии имеет вид: y = 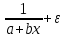 4.Укажите, по какой формуле вычисляется выборочный коэффициент парной корреляции rxy. Ответ: 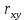 =b =b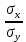 = =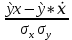 5.Объясните сущность метода анализа динамического ряда. Ответ: Динамические ряды, характеризуют каждый момент времени в отдельности, а не весь период, для которого строится модель. Эконометрическая модель является динамической, если в данный период времени она учитывает значения входящих в нее переменных, относящихся как к текущему, так и к предыдущему периоду времени, то есть если эта модель отражает динамику исследуемых переменных в каждый момент времени. Сущность метода анализа динамического ряда заключается в том, что при сравнении двух уровней, показать разницу между данным уровнем и уровнем базисного периода. Задача №1 1.Рассчитать коэффициенты для различных видов зависимостей. Исходные данные в табл.3 Таблица 3. Регрессионный анализ.
Вариант № 1 y = a+bx
a * n + b Ʃ x=Ʃ y a *Ʃ x + b Ʃ 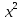 =Ʃ x y =Ʃ x y5a+150 b = 450.02 150a + 5500b = 19670.6 a = - 95.096b = 6.17 y = a + b x = - 95.096 + 6.17 x Вариант № 2 y = a+bx
a * n + b Ʃ x=Ʃ y a *Ʃ x + b Ʃ 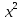 =Ʃ x y =Ʃ x y5a+150 b = 350 150a + 5500b = 12500 a = 10b = 2 y = a + b x = 10 + 2x Вариант № 3 y = a+bx
a * n + b Ʃ x=Ʃ y a *Ʃ x + b Ʃ 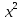 =Ʃ x y =Ʃ x y5a+150 b = 521.93 150a + 5500b = 19921.4 a = - 23.519b = 4.2635 y = a + b x = -23.519 + 4.2635x Вариант № 4 y = a+bx
a * n + b Ʃ x=Ʃ y a *Ʃ x + b Ʃ 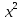 =Ʃ x y =Ʃ x y5a+150 b = 257.08 150a + 5500b = 5244.3 a = 125.459b = - 2.4681 y = a + b x = 125.459 – 2.4681 x Вариант № 5 y = a+bx
a * n + b Ʃ x=Ʃ y a *Ʃ x + b Ʃ 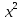 =Ʃ x y =Ʃ x y5a+150 b = 248.47 150a + 5500b = 3673.4 a = 163.115b = - 3.7807 y = a + b x = 163.115 – 3.7807 x Задача № 2 Вычислить коэффициент корреляции для линейной зависимости. Исходные данные в таблице 4. Таблица 4. Корреляционный анализ.
Вариант № 1
a * n + b Ʃ x=Ʃ y ʹx = 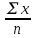 = = 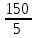 = 30 = 30a *Ʃ x + b Ʃ 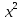 =Ʃ xy ʹy = =Ʃ xy ʹy = 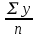 = = 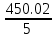 = 90.004 = 90.0045a+150 b = 450.02 xʹy = 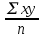 = =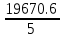 = 3934.12 = 3934.12 150a + 5500b = 19670.6 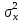 = = 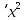 - -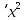 = = 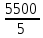 - 900 = 200 - 900 = 200a = - 95.096b = 6.17 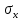 = = 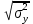 = = 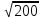 = 14.142 = 14.142 y = a + b x = - 95.096 + 6.17 x 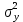 = =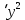 - -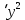 = = 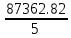 – 8100.72 = 9371.85 – 8100.72 = 9371.85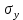 = = 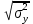 = = 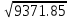 = 96.808 = 96.808 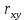 =b =b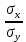 = =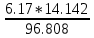 =0.901 =0.901Вариант № 2
a * n + b Ʃ x=Ʃ y ʹx = 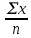 = = 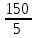 = 30 = 30a *Ʃ x + b Ʃ 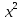 =Ʃ x y ʹy = =Ʃ x y ʹy = 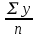 = = 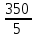 = 70 = 705a+150 b = 350 xʹy = 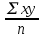 = =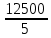 = 2500 = 2500 150a + 5500b = 12500 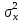 = = 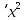 - -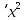 = = 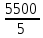 - 900 = 200 - 900 = 200a = 10b = 2 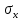 = = 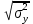 = = 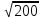 = 14.142 = 14.142 y = a + b x = 10 + 2x 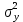 = =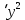 - -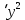 = = 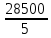 – 4900 = 800 – 4900 = 800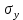 = = 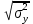 = = 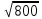 = 28.284 = 28.284 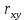 =b =b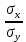 = =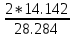 =1 =1Вариант № 3
a * n + b Ʃ x=Ʃ y ʹx = 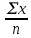 = = 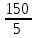 = 30 = 30 a *Ʃ x + b Ʃ 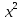 =Ʃ x y ʹy = =Ʃ x y ʹy = 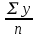 = = 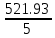 = 104.386 = 104.3865a+150 b = 521.93 xʹy = 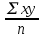 = =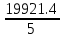 = 3984.28 = 3984.28 150a + 5500b = 19921.4 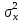 = = 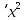 - -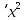 = = 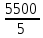 - 900 = 200 - 900 = 200a = - 23.519b = 4.2635 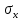 = = 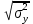 = = 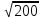 = 14.142 = 14.142 y = a + b x = -23.519 + 4.2635x 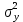 = =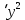 - -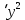 = = 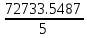 – 10896.437 =3650.27 – 10896.437 =3650.27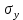 = = 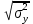 = = 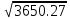 = 60.417 = 60.417 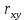 =b =b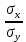 = =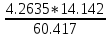 =0.998 =0.998Вариант № 4
a * n + b Ʃ x=Ʃ y ʹx = 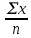 = = 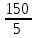 = 30 = 30a *Ʃ x + b Ʃ 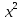 =Ʃ x y ʹy = =Ʃ x y ʹy = 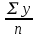 = = 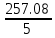 = 51.416 = 51.4165a+150 b = 257.08 xʹy = 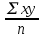 = =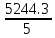 = 1048.86 = 1048.86 150a + 5500b = 5244.3 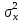 = = 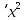 - -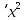 = = 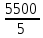 - 900 = 200 - 900 = 200a = 125.459b = - 2.4681 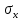 = = 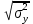 = = 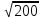 = 14.142 = 14.142 y = a + b x = 125.459 – 2.4681 x 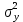 = =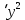 - -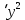 = = 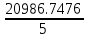 – 264.605 =1553.74 – 264.605 =1553.74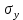 = = 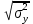 = = 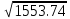 = 39.418 = 39.418 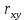 =b =b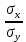 = =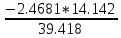 = - 0.885 = - 0.885Вариант № 5
a * n + b Ʃ x=Ʃ y ʹx = 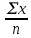 = = 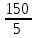 = 30 = 30a *Ʃ x + b Ʃ 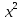 =Ʃ x y ʹy = =Ʃ x y ʹy = 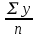 = = 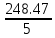 = 49.694 = 49.6945a+150 b = 248.47 xʹy = 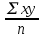 = =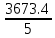 = 734.68 = 734.68 150a + 5500b = 3673.4 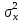 = = 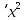 - -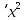 = = 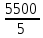 - 900 = 200 - 900 = 200a = 163.115b = - 3.7807 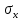 = = 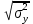 = = 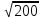 = 14.142 = 14.142 y = a + b x = 163.115 – 3.7807 x 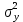 = =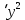 - -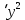 = = 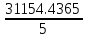 – 2469.494=3761.39 – 2469.494=3761.39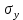 = = 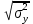 = = 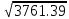 = 61.33 = 61.33 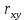 =b =b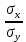 = =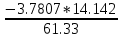 = - 0.872 = - 0.872 |