3 ОБОСНОВАНИЕ ВЫЧИСЛИТЕЛЬНОЙ ПРОЦЕДУРЫ
Для большинства методов решения задач линейного программирования требуется предварительно привести задачу к стандартной форме. Задача (или ее математическая модель) представлена в стандартной форме, если она соответствует следующим условиям:
целевая функция подлежит максимизации;
все ограничения имеют вид равенств;
на все переменные накладываются ограничения неотрицательности.
Для решения данной задачи воспользуемся симплекс- методом. Так как в математической модели не присутствуют ограничения вида «больше или равно», то для решения задачи достаточно будет обычного симплекс-метода. Поиск целочисленного решения не требуется, так как все переменные задачи по своему физическому смыслу могут принимать нецелочисленные значения.
ПРИНЦИП РАБОТЫ СИМПЛЕКС- МЕТОДА
Симплекс-метод позволяет решать задачи линейного программирования любой размерности, т.е. с любым количеством переменных. Решение задач линейного программирования на основе симплекс-метода состоит в целенаправленном переборе угловых точек ОДР в направлении улучшения значения целевой функции.
Можно доказать, что экстремум (минимум или максимум) целевой функции всегда достигается при значениях переменных X1, X2,...,Xn, соответствующих одной из угловых точек ОДР. Другими словами, оптимальное решение всегда находится в угловой точке ОДР.
Принцип работы симплекс- метода состоит в следующем. Находится какое- либо допустимое решение, соответствующее одной из угловых точек ОДР. Проверяются смежные с ней угловые точки ОДР. Если ни в одной изсмежных угловых точек значение целевой функции не улучшается, то решение задачи завершается; текущая угловая точка ОДР соответствует оптимальному решению задачи. Если имеются смежные угловые точки ОДР, для которых значение целевой функции улучшается, то выполняется переход в ту из них, для которой достигается наиболее быстрое улучшение значения целевой функции. Для новой угловой точки ОДР процесс повторяется, т.е. проверяются смежные угловые точки. Перебор угловых точек происходит до тех пор, пока не будет найдено оптимальное решение, т.е. пока не будет достигнута угловая точка ОДР, для которой ни в одной из смежных точек значение целевой функции не улучшается.
Поиск решения на основе симплекс-метода реализуется путем вычислений на симплекс-таблицах. Основные этапы реализации симплекс- метода следующие.
Задача линейного программирования приводится к стандартной форме.
Определяется начальное допустимое решение (начальная угловая точка ОДР).
Строится исходная симплекс- таблица. Выполняются преобразования симплекс-таблиц, соответствующие перебору угловых точек ОДР, до получения оптимального решения.
Реализация симплекс- метода существенно различается в зависимости от вида математической модели задачи.
4 РЕШЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ НА ОСНОВЕ СИМПЛЕКС-МЕТОДА
Приведем задачу к стандартной форме. Для этого во все ограничения типа «меньше или равно» вводятся остаточные переменные, а в ограничения типа «больше или равно» – избыточные переменны. Математическая модель задачи в стандартной форме будет иметь следующий вид:
-0,81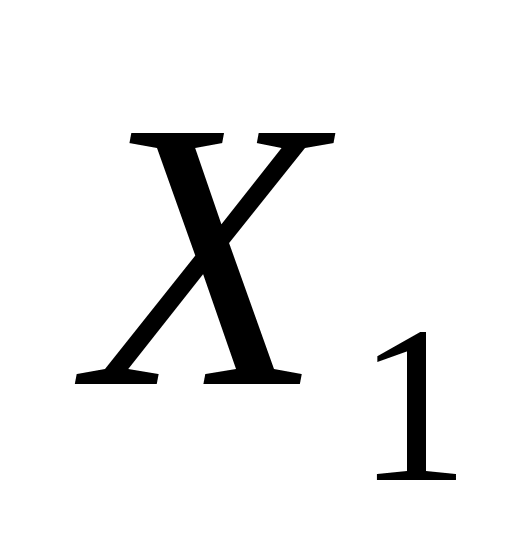 +0,085 +0,085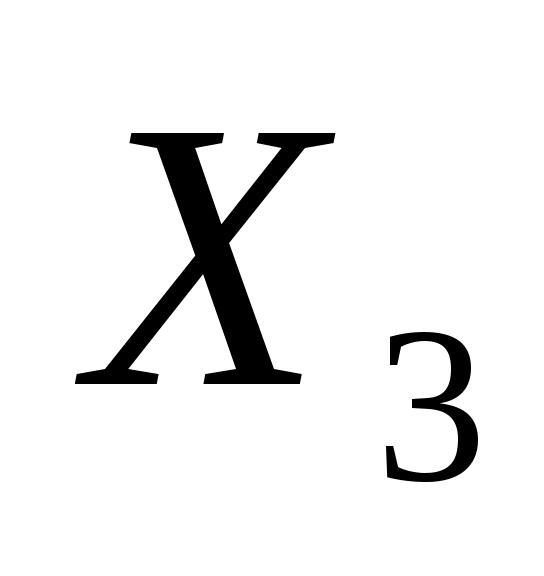 + +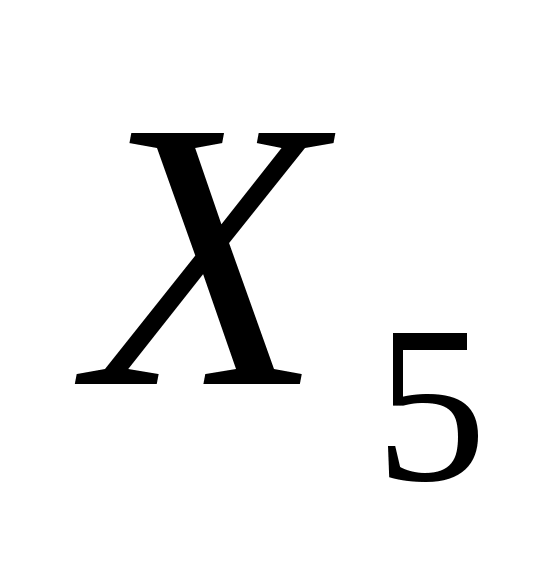 =0 =0
-0,77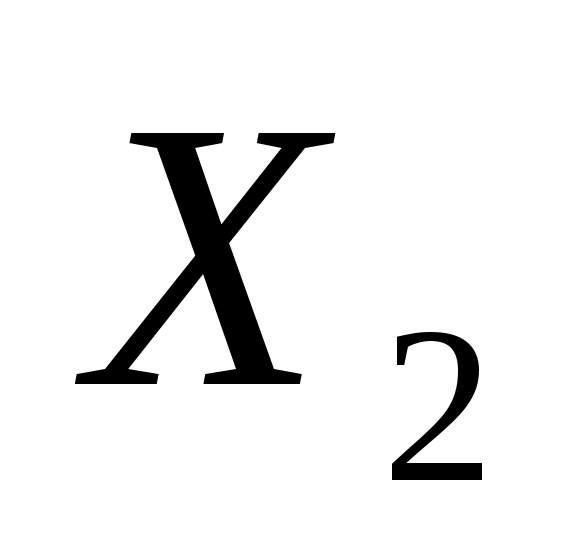 +0,13 +0,13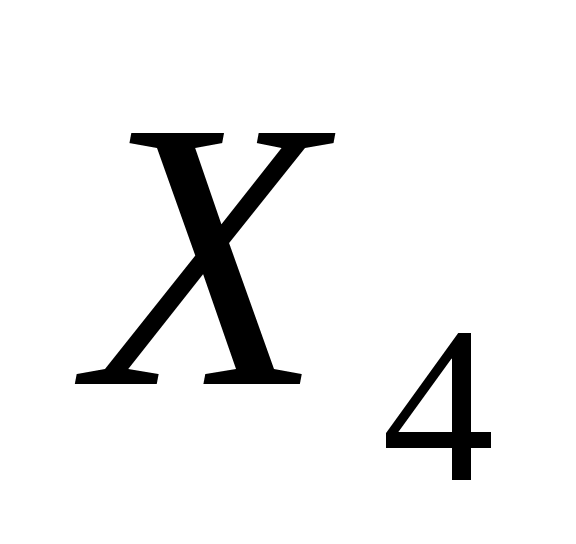 + +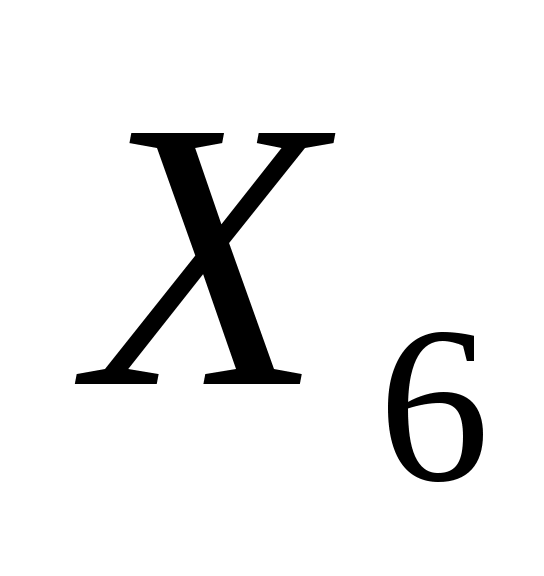 =0 =0
-0,23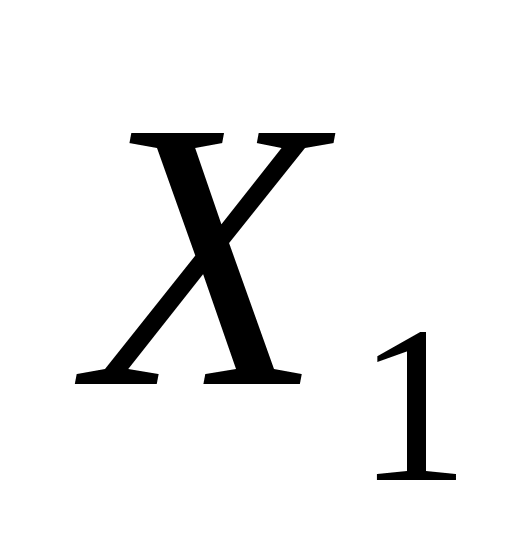 +0,64 +0,64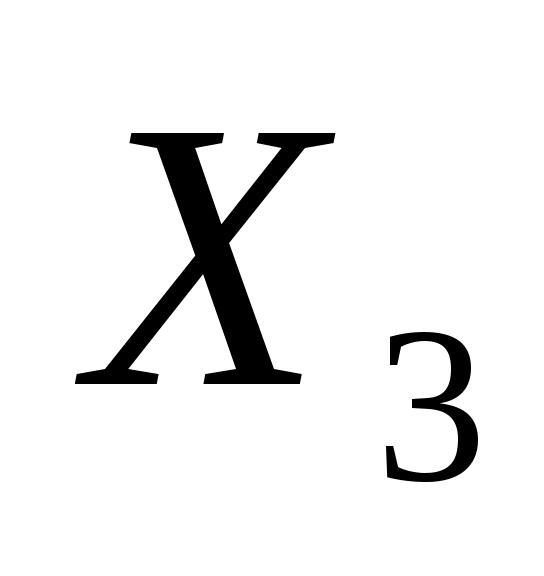 + +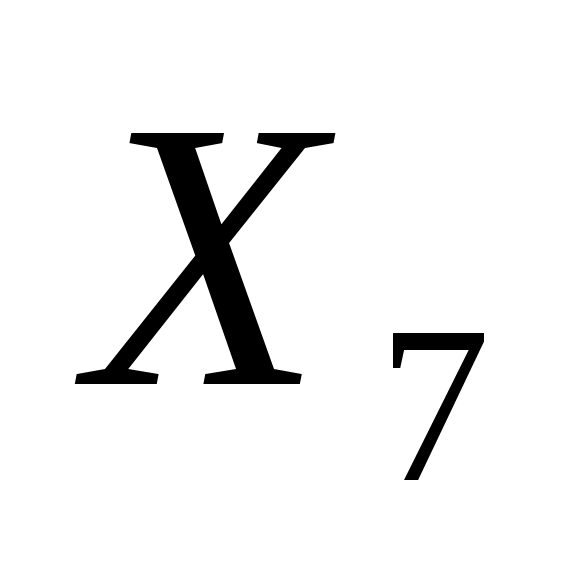 =0 =0
0,9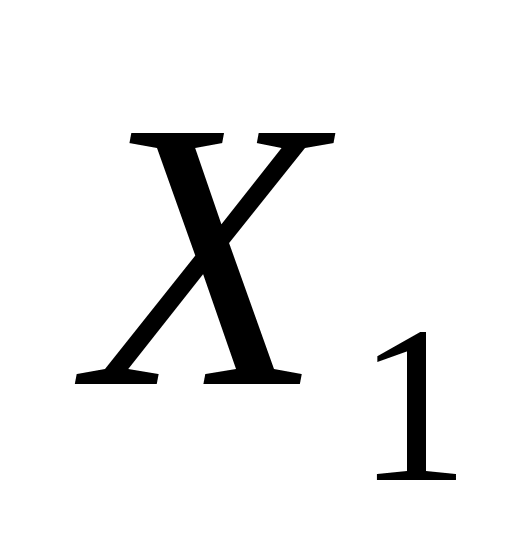 +0,85 +0,85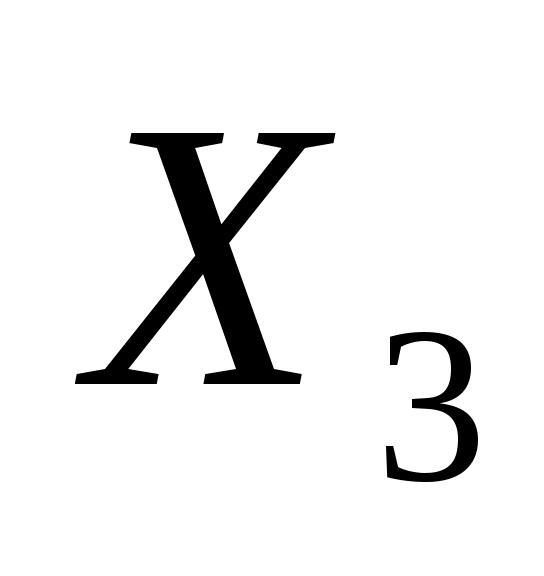 + +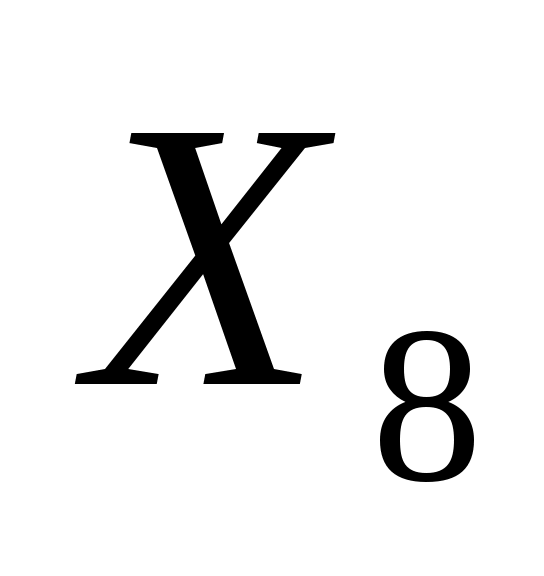 =100000 =100000
0,9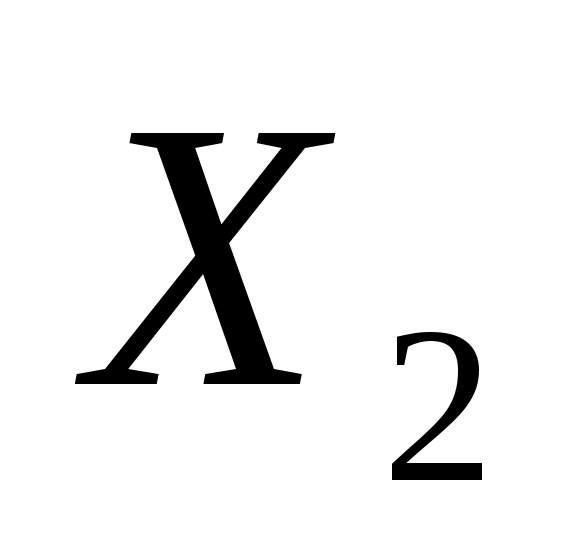 +0,85 +0,85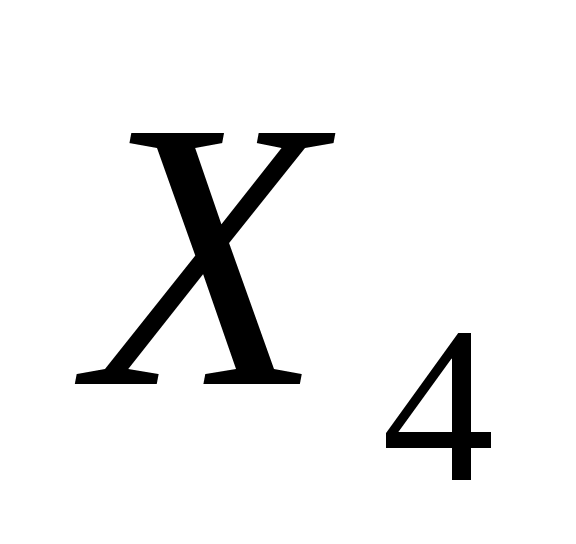 + +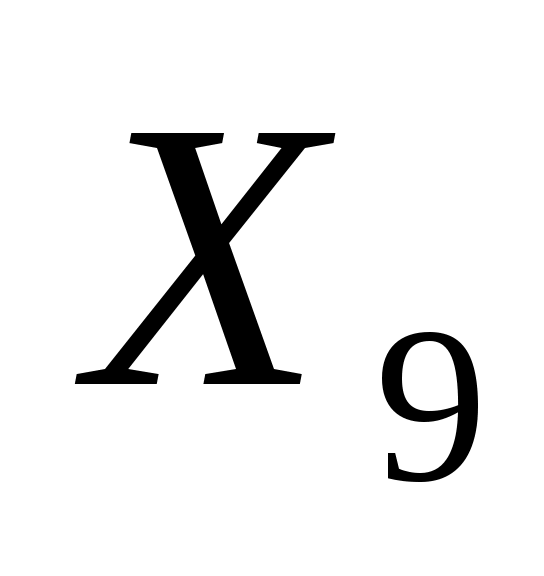 =120000 =120000
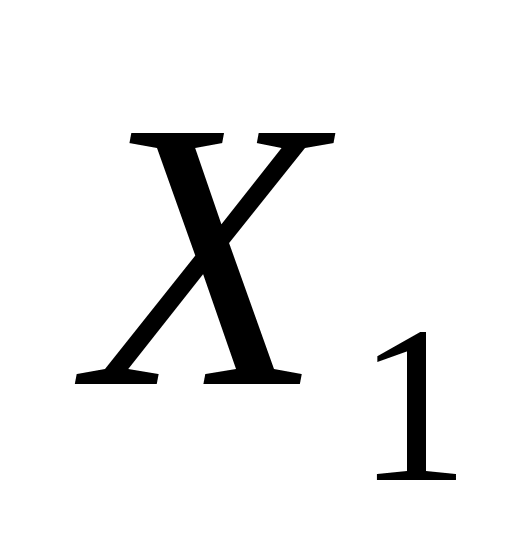 , , 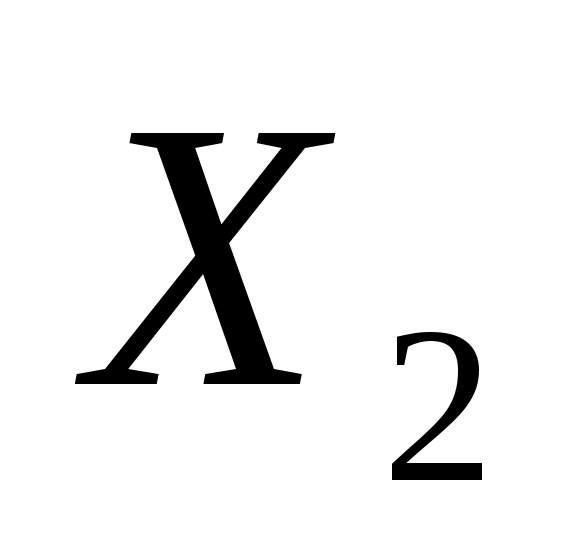 , , 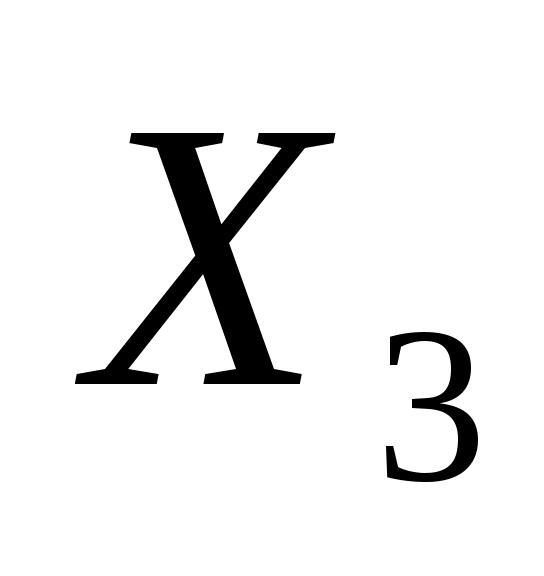 , , 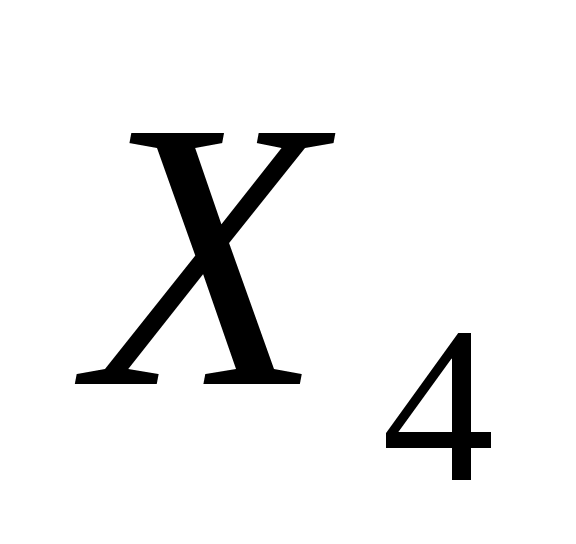 , , 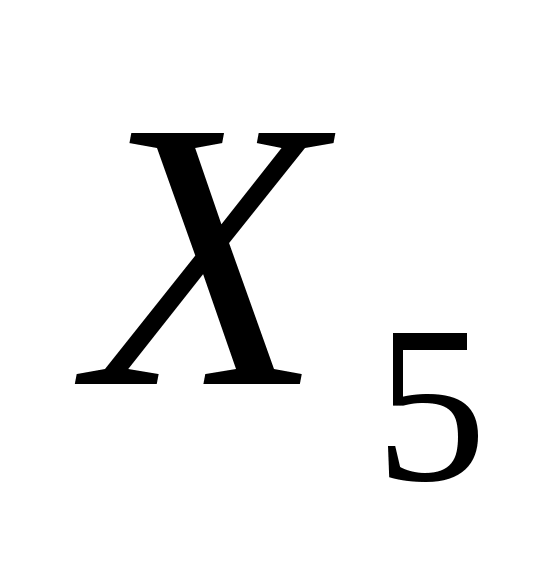 , , 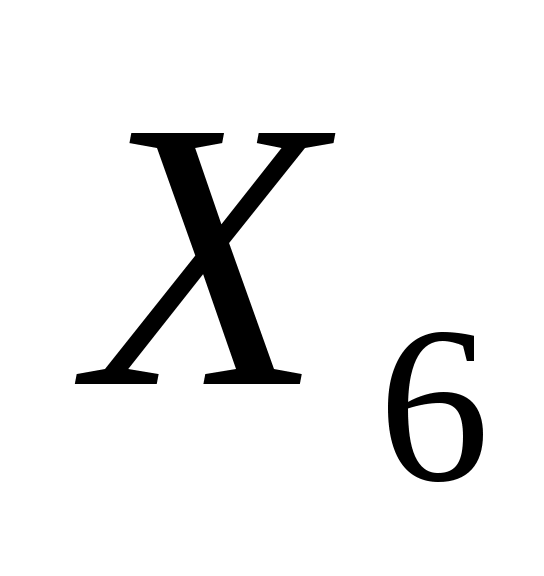 , , 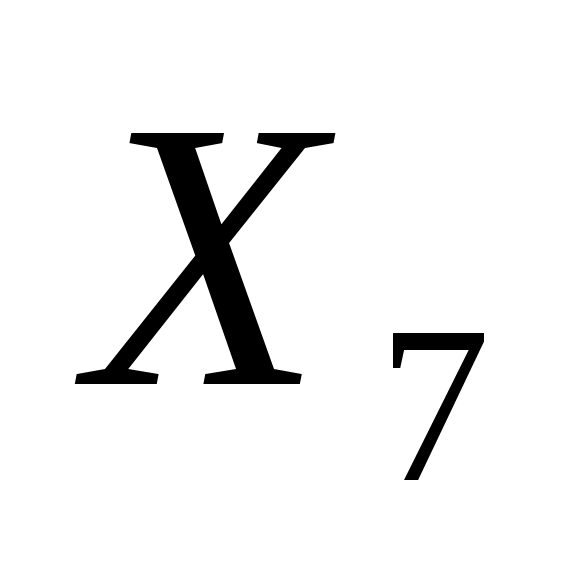 , , 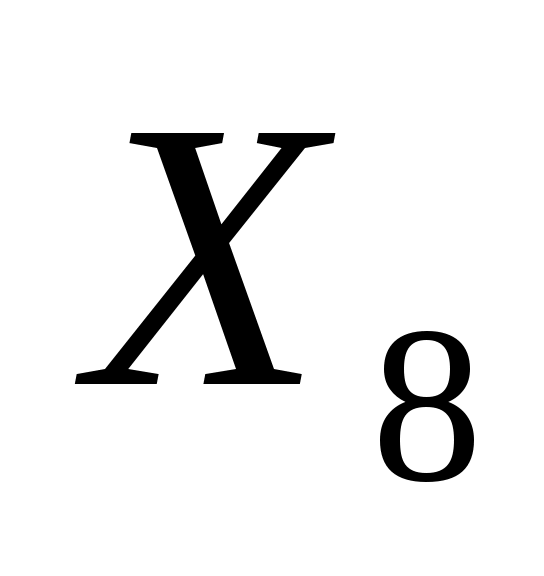 , , 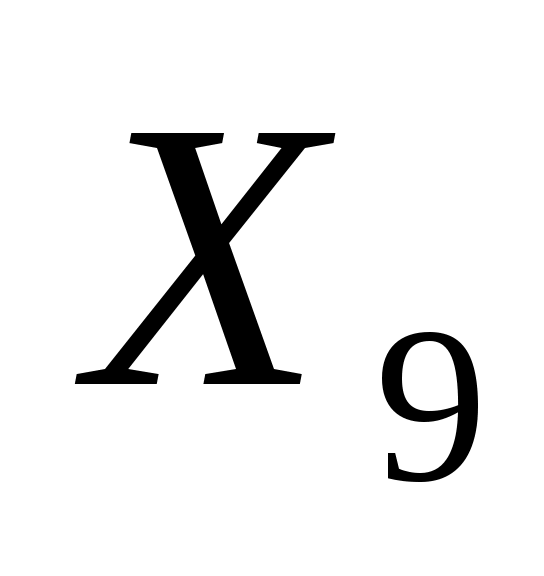 ≥0 ≥0
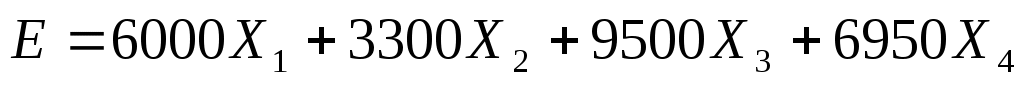 →max →max
Здесь 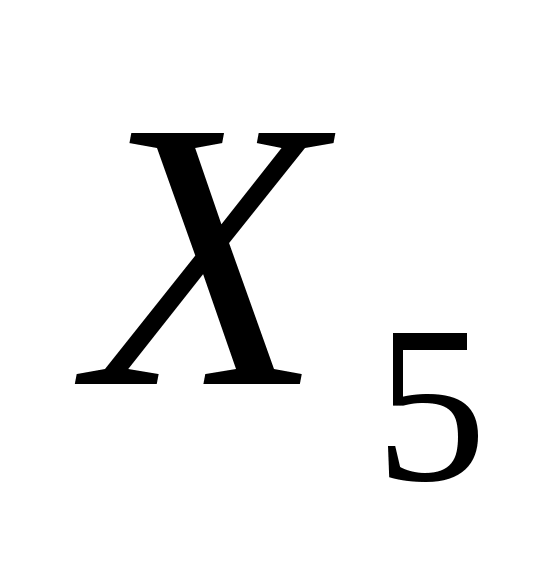 , , 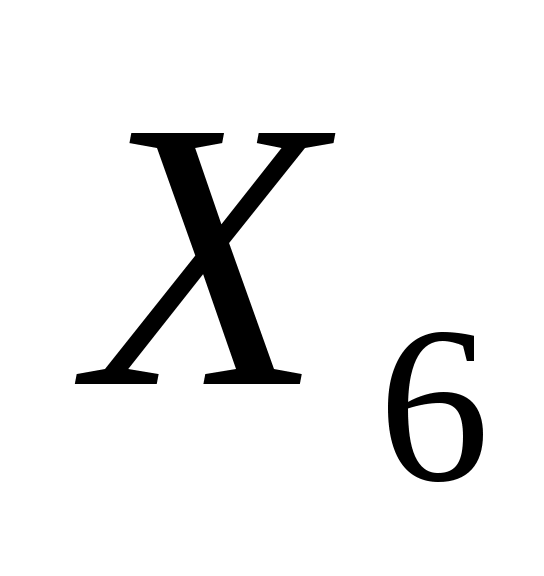 , , 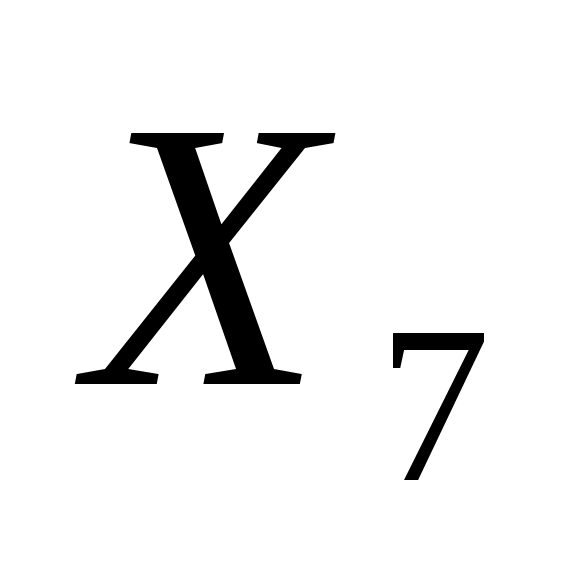 , , 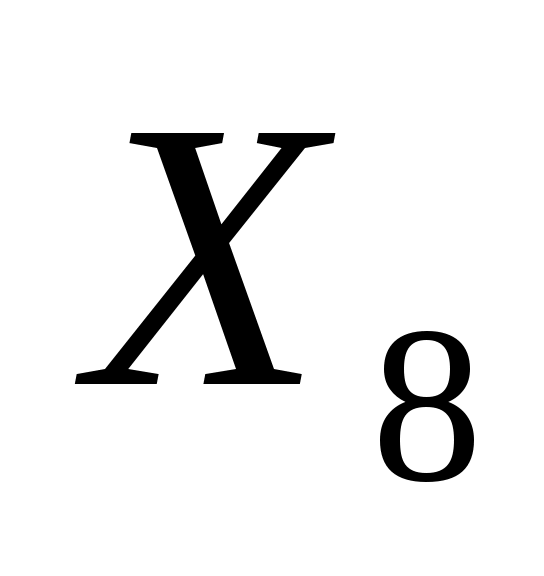 , , 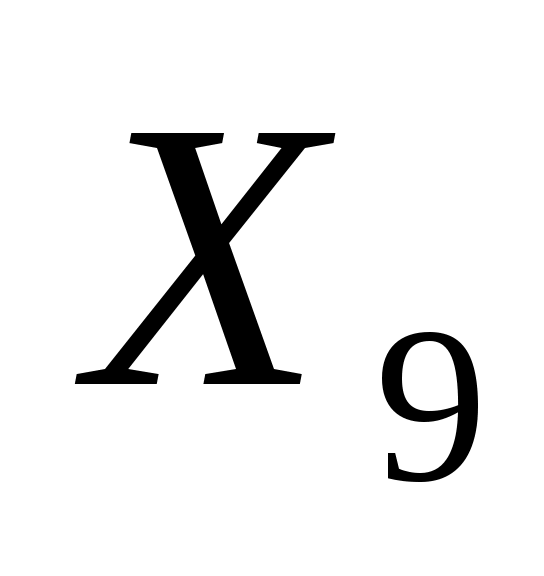 - остаточные переменные. - остаточные переменные.
В качестве базисных переменных выбираем 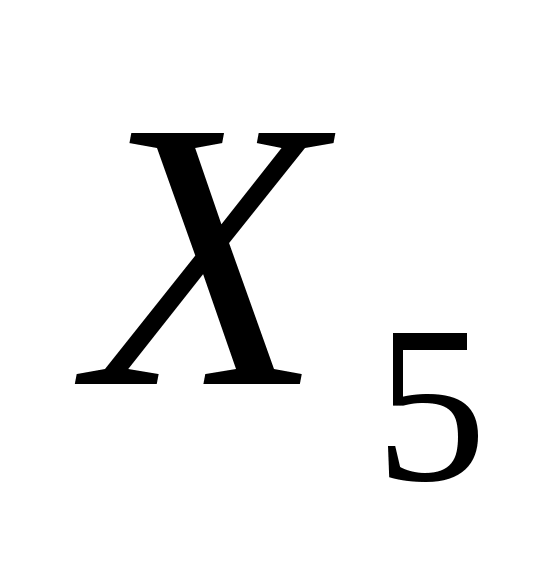 , , 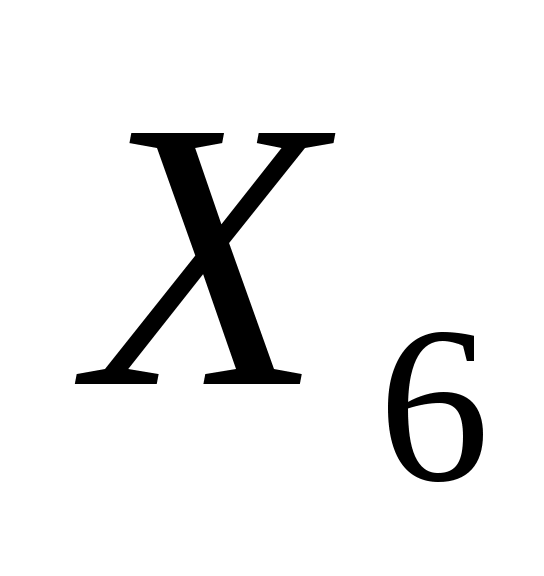 , , 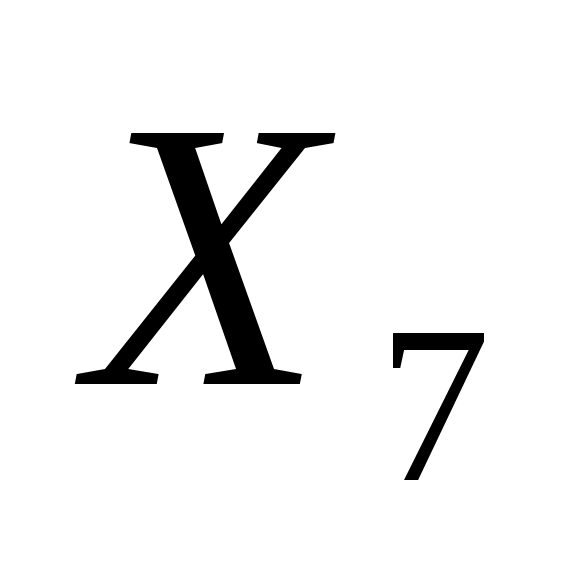 , , 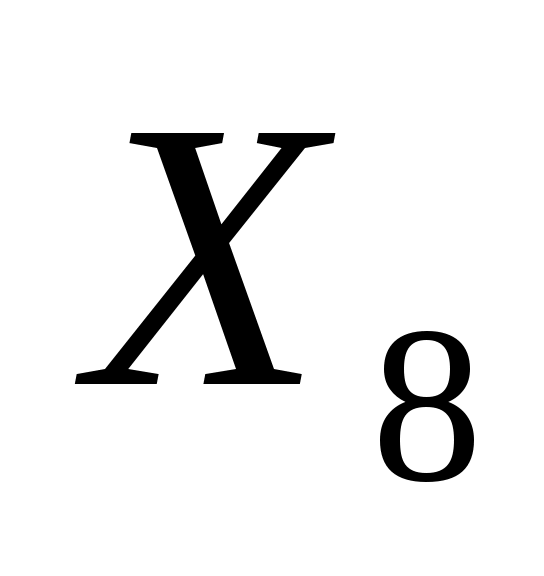 и и 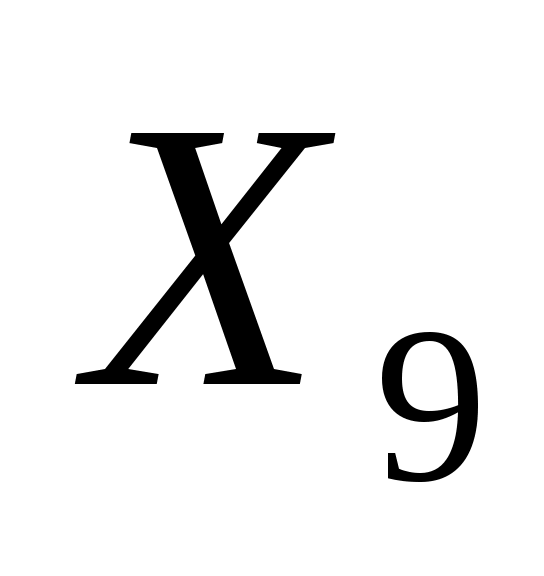 , так как каждая из них входит только в одно ограничение с коэффициентом, равным единице, и не входит в другие ограничения. Базисные переменные имеются во всех ограничениях задачи. , так как каждая из них входит только в одно ограничение с коэффициентом, равным единице, и не входит в другие ограничения. Базисные переменные имеются во всех ограничениях задачи.
Определим начальное решение. Все исходные переменные задачи являются небазисными, т.е. принимаются равными нулю (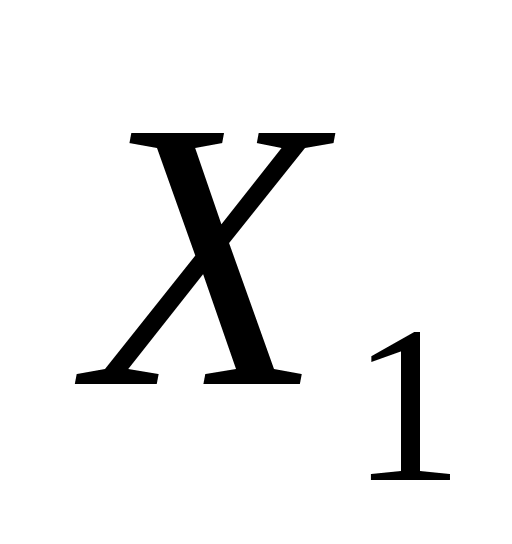 = =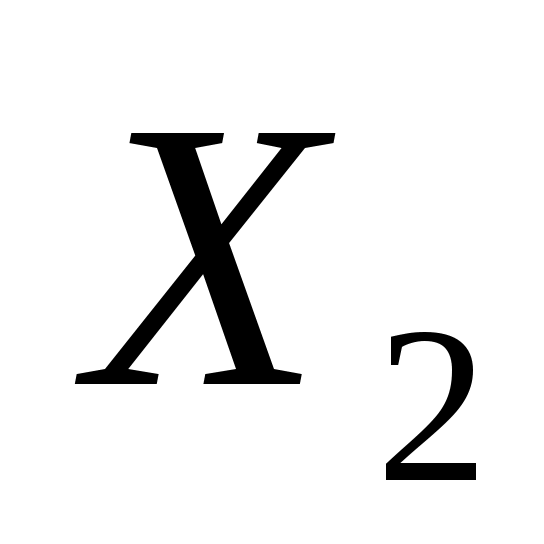 = =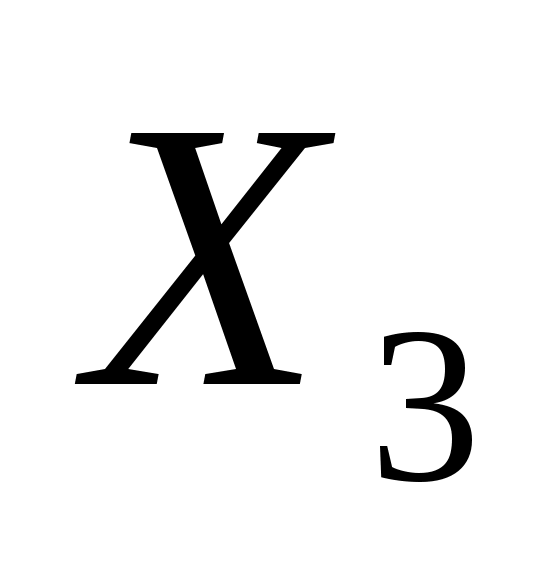 = =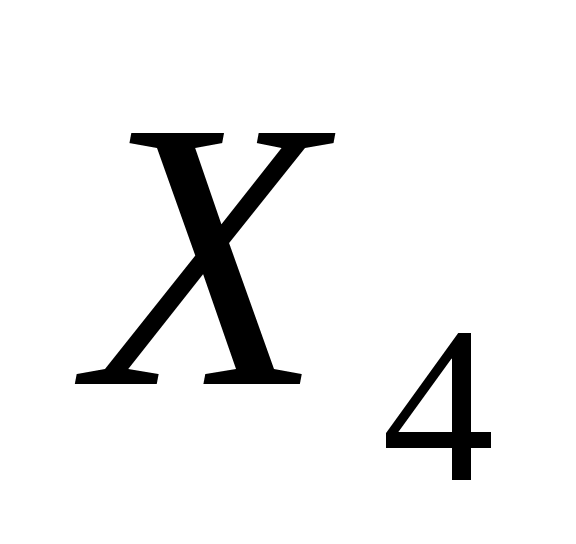 =0). Таким образом, начальное решение задачи следующее: =0). Таким образом, начальное решение задачи следующее:
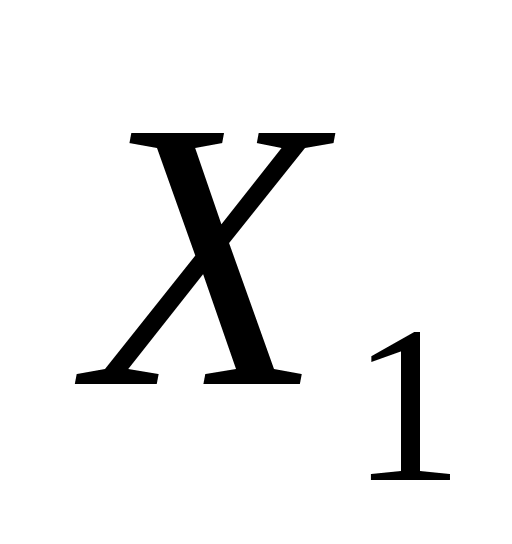 =0, =0, 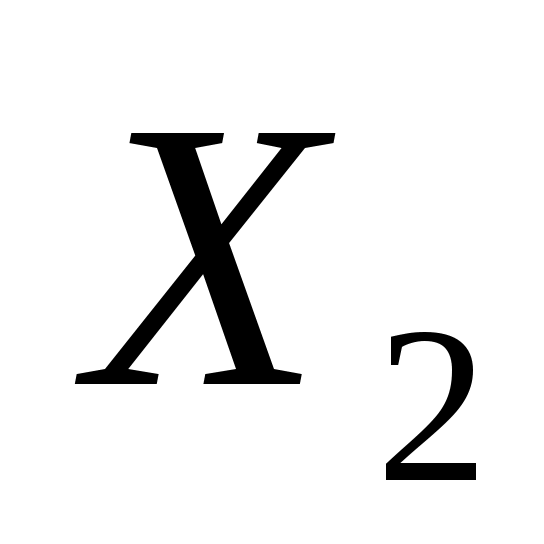 =0, =0, 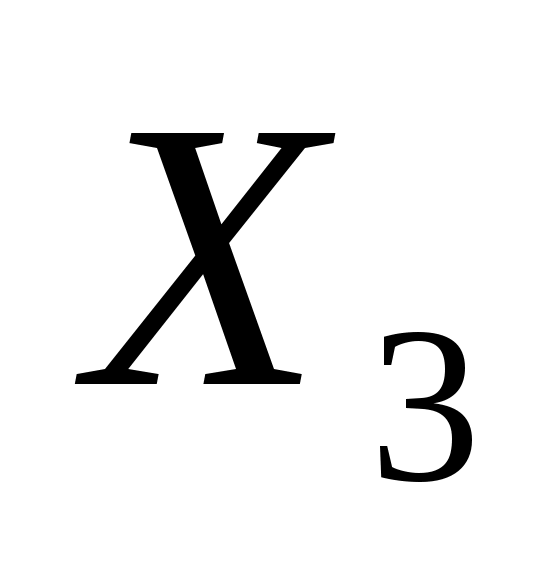 =0, =0, 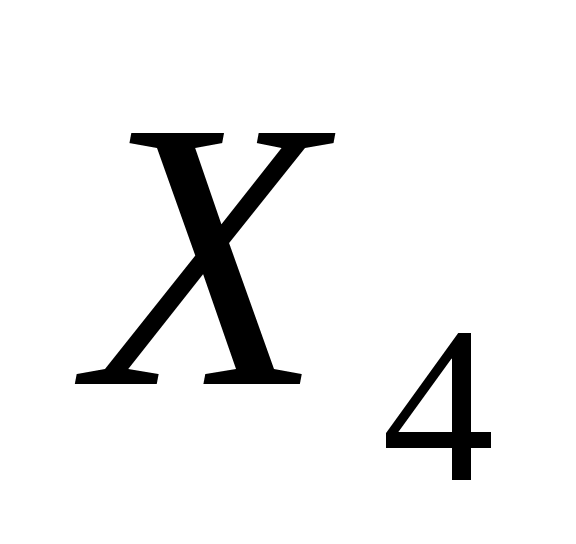 =0, =0, 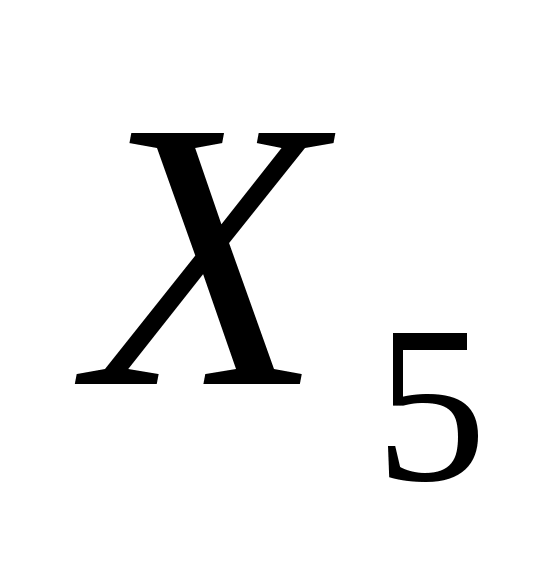 =0, =0, 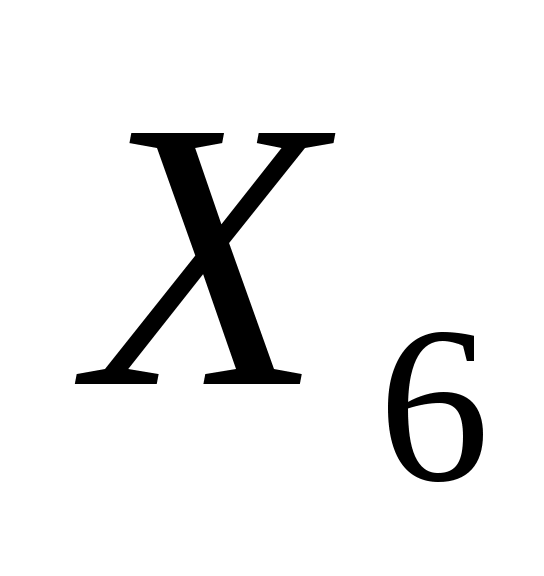 =0, =0, 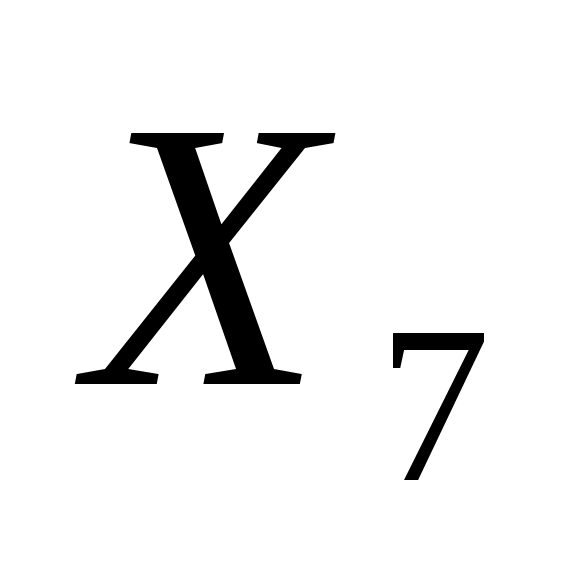 =0, =0, 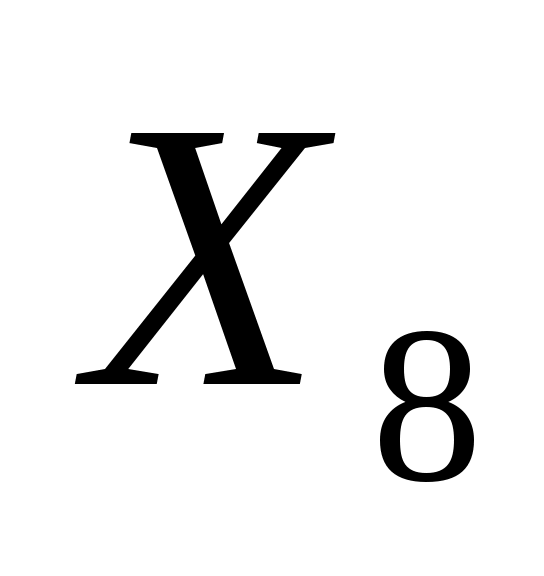 =100000, =100000, 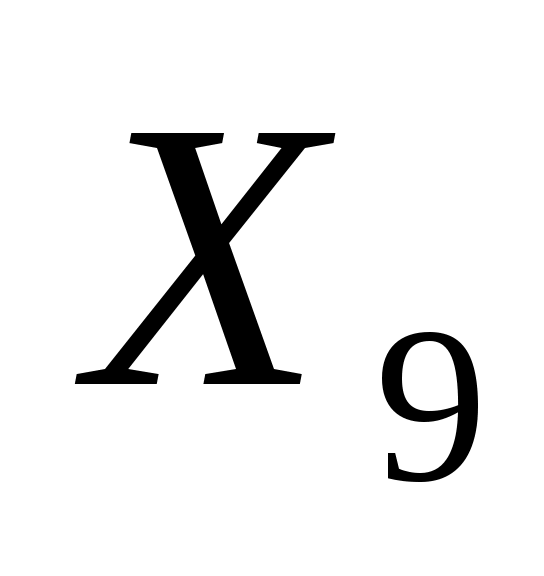 =120000. =120000.
В соответствии с преобразованной математической моделью, это решение является допустимым, так как значения 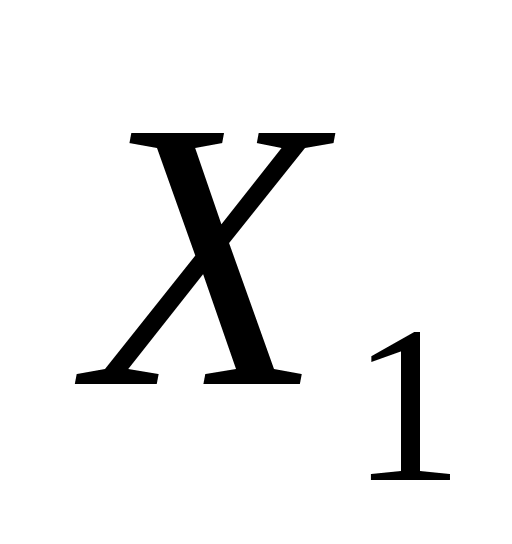 = =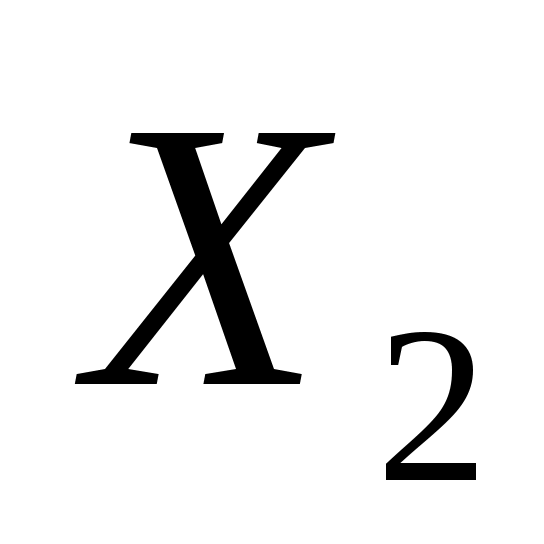 = =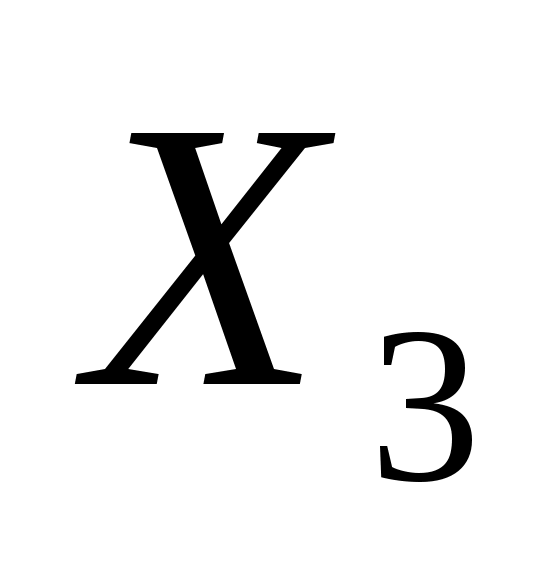 = =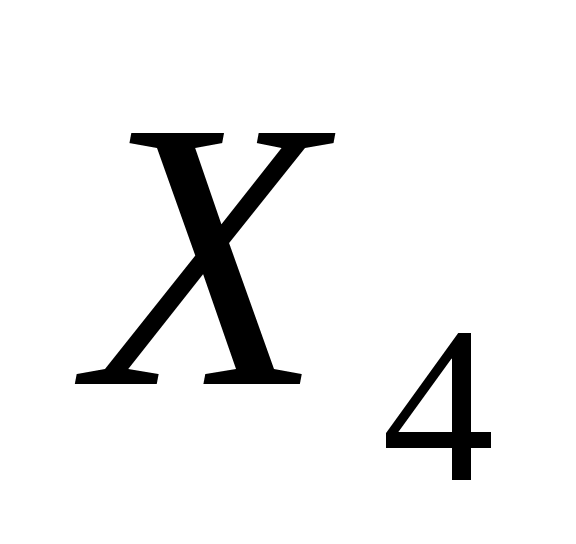 =0 соответствует преобразованной системе ограничений. =0 соответствует преобразованной системе ограничений.
Выбранное решение не является оптимальным, так как целевая функция 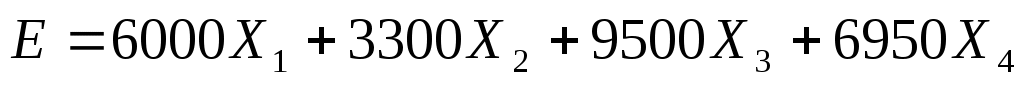 при этом равна нулю. По своему смыслу это решение означает, что смазочные материалы не выпускаются. при этом равна нулю. По своему смыслу это решение означает, что смазочные материалы не выпускаются.
Составим исходную симплекс-таблицу.
Таблица 4.1 – симплекс- таблица №1
БП
|
X 1
|
X 2
|
X 3
|
X 4
|
X 5
|
X 6
|
X 7
|
X 8
|
X 9
|
БР
|
E
|
-6000
|
-3300
|
-9500
|
-6950
|
0
|
0
|
0
|
0
|
0
|
0
|
X 5
|
-0,81
|
0
|
0,085
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
X 6
|
0
|
-0,77
|
0
|
0,13
|
0
|
1
|
0
|
0
|
0
|
0
|
X 7
|
-0,23
|
0
|
0,64
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
X 8
|
0,9
|
0
|
0,85
|
0
|
0
|
0
|
0
|
1
|
0
|
100000
|
X 9
|
0
|
0,9
|
0
|
0,85
|
0
|
0
|
0
|
0
|
1
|
120000
|
Выбираем переменную для включения в базис. В базис включается переменная, которой соответствует максимальный по модулю отрицательный элемент в E-строки. Включение в базис такой переменной приводит к наиболее быстрому росту целевой функции. Столбец соответствующий этой переменной становится ведущим. На данный момент это столбец 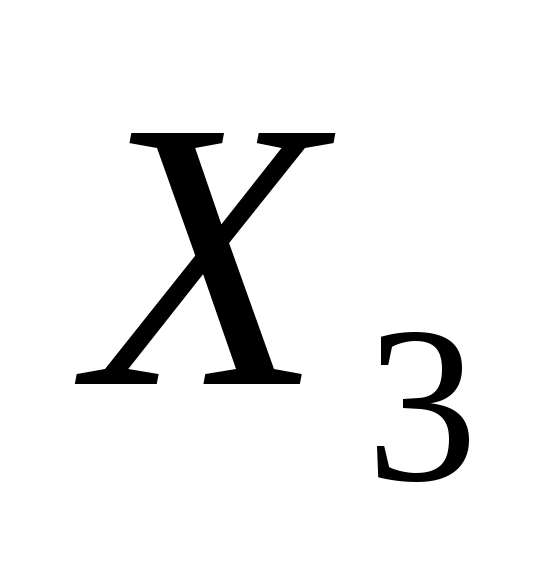 , т.к. именно в нем содержится максимальный по модулю отрицательный коэффициент (-9500). Далее определяем ведущую строку. Ведущая строка определяется с помощью симплекс-отношений, отношений элементов столбца базисных решений «БР» к элементам ведущего столбца. Выбирается минимальное из отношений, та строка, которой оно соответствует, является ведущей. , т.к. именно в нем содержится максимальный по модулю отрицательный коэффициент (-9500). Далее определяем ведущую строку. Ведущая строка определяется с помощью симплекс-отношений, отношений элементов столбца базисных решений «БР» к элементам ведущего столбца. Выбирается минимальное из отношений, та строка, которой оно соответствует, является ведущей. 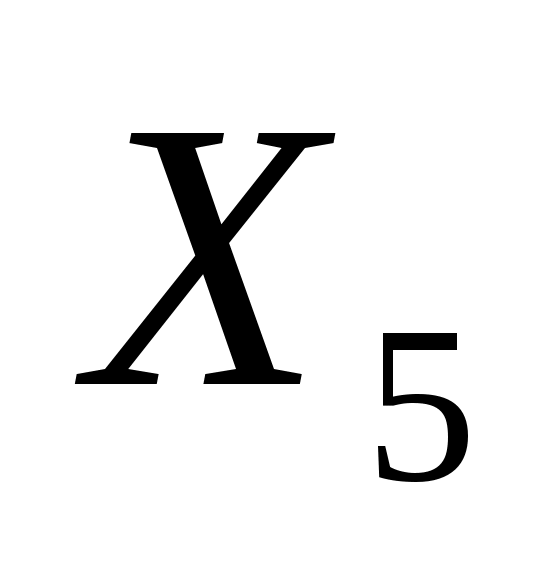 :0/0,085=0; :0/0,085=0; 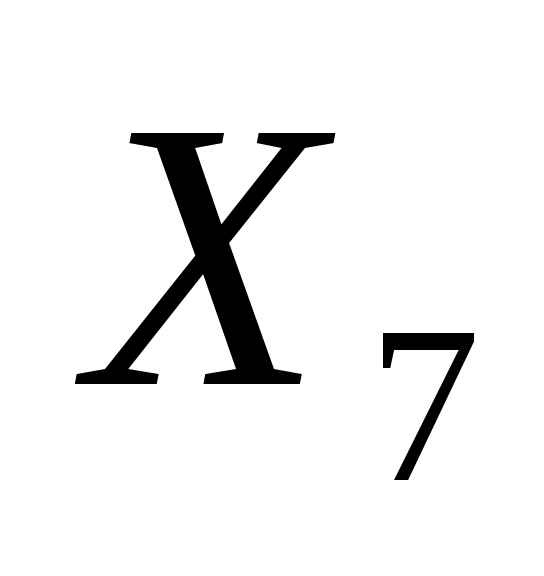 :0/0,64=0; :0/0,64=0; 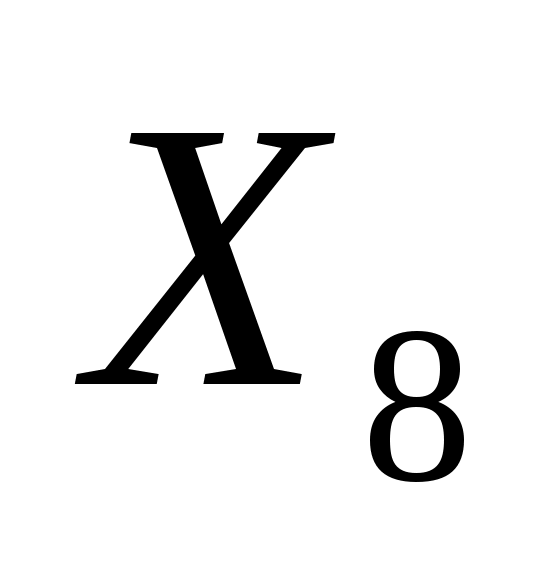 :100000/0,85=117647; Получено два минимальных отношения для переменных :100000/0,85=117647; Получено два минимальных отношения для переменных 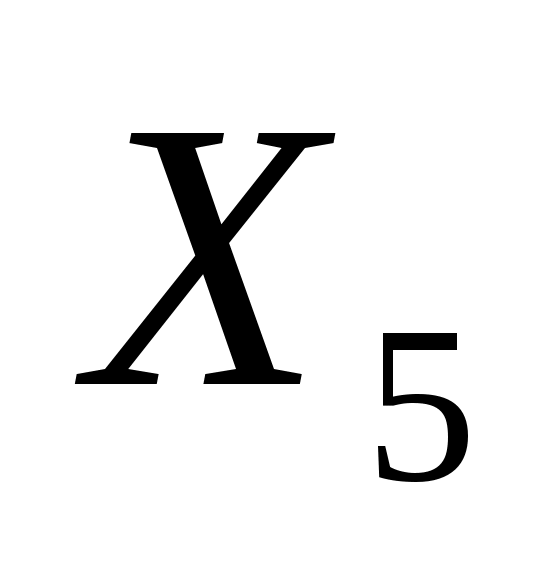 и и 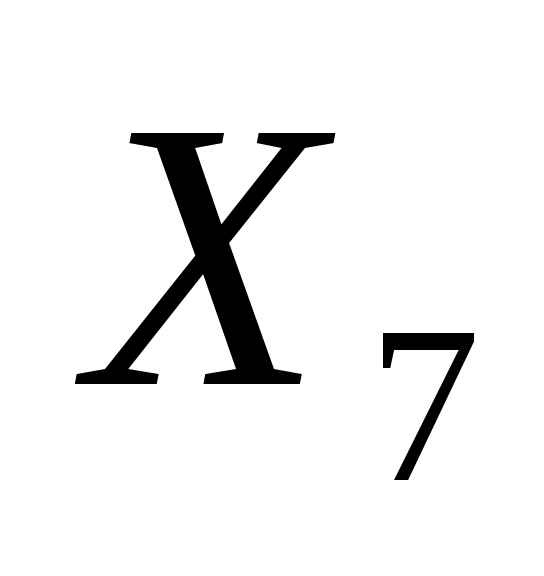 , в качестве ведущей строки можно выбрать любую из них, пусть , в качестве ведущей строки можно выбрать любую из них, пусть 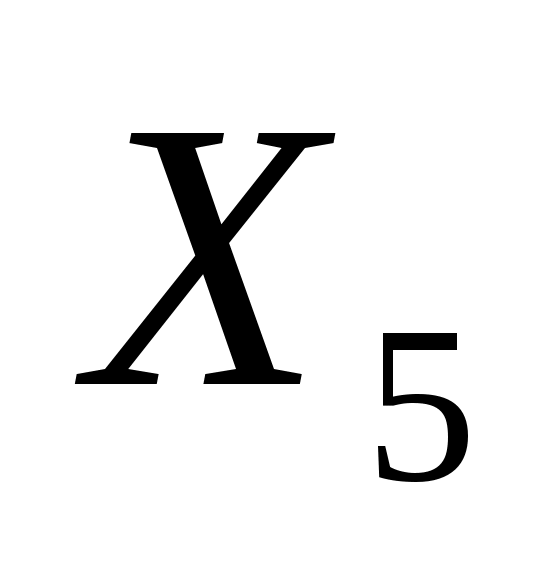 – ведущая строка. Определяем ведущий элемент, он находится на пересечении ведущего столбца и строки (ведущий элемент 0,085). – ведущая строка. Определяем ведущий элемент, он находится на пересечении ведущего столбца и строки (ведущий элемент 0,085).
Таким образом, переменная 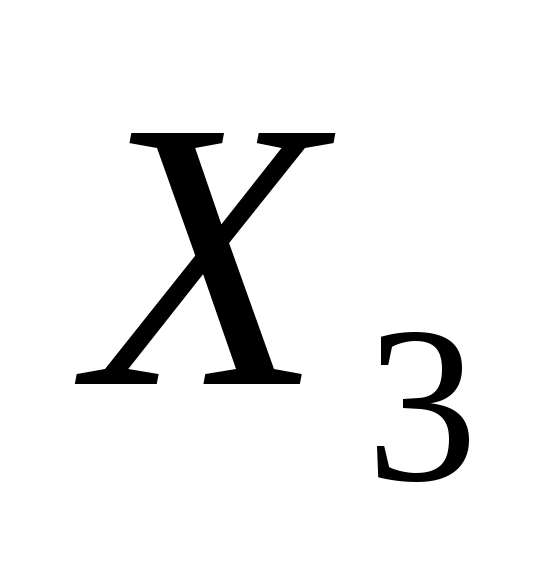 включается в базис, так как ей соответствуем максимальный по модулю отрицательный коэффициент E-строки. включается в базис, так как ей соответствуем максимальный по модулю отрицательный коэффициент E-строки. 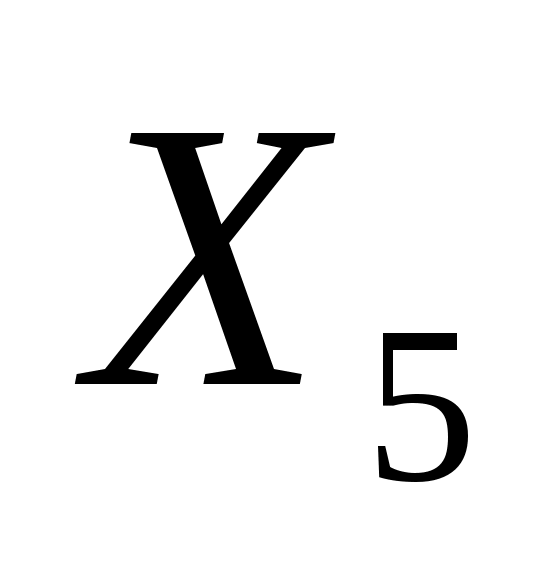 исключается из базиса, так как ей соответствует минимальное симплекс отношение. Далее все элементы ведущей строки делятся на ведущий элемент, а все элементы ведущего столбца (кроме ведущего элемента) заменяются нулями. Все остальные элементы таблицы (включая E-строку и столбец “Решение”) пересчитываются по “правилу прямоугольника”. Этот пересчет выполняется следующим образом: ведущий и пересчитываемый элемент образуют диагональ прямоугольника; находится произведение ведущего и пересчитываемого прямоугольника; из этого произведения вычитается произведение элементов, образующих противоположную диагональ прямоугольника; результат делится на ведущий элемент. В результате расчетов получаем новую симплекс-таблицу: исключается из базиса, так как ей соответствует минимальное симплекс отношение. Далее все элементы ведущей строки делятся на ведущий элемент, а все элементы ведущего столбца (кроме ведущего элемента) заменяются нулями. Все остальные элементы таблицы (включая E-строку и столбец “Решение”) пересчитываются по “правилу прямоугольника”. Этот пересчет выполняется следующим образом: ведущий и пересчитываемый элемент образуют диагональ прямоугольника; находится произведение ведущего и пересчитываемого прямоугольника; из этого произведения вычитается произведение элементов, образующих противоположную диагональ прямоугольника; результат делится на ведущий элемент. В результате расчетов получаем новую симплекс-таблицу:
Таблица 4.2 – симплекс- таблица №2
БП
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
X8
|
X9
|
БР
|
E
|
-96529
|
-3300
|
0
|
-6950
|
111765
|
0
|
0
|
0
|
0
|
0
|
X3
|
-9,53
|
0
|
1
|
0
|
11,77
|
0
|
0
|
0
|
0
|
0
|
X6
|
0
|
-0,77
|
0
|
0,13
|
0
|
1
|
0
|
0
|
0
|
0
|
X7
|
5,87
|
0
|
0
|
0
|
-7,53
|
0
|
1
|
0
|
0
|
0
|
X8
|
9
|
0
|
0
|
0
|
-10
|
0
|
0
|
1
|
0
|
100000
|
X9
|
0
|
0,9
|
0
|
0,85
|
0
|
0
|
0
|
0
|
1
|
120000
|
Полученное решение не является оптимальным: в строке целевой функции имеется отрицательные элементы. Поэтому решение продолжается. Ведущий столбец соответствует переменной 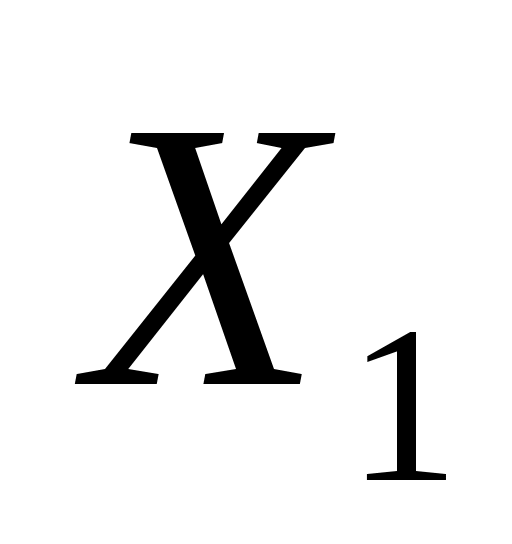 , у нее максимальный по модулю отрицательный коэффициент в строке целевой функции. Симплексные отношения: , у нее максимальный по модулю отрицательный коэффициент в строке целевой функции. Симплексные отношения:
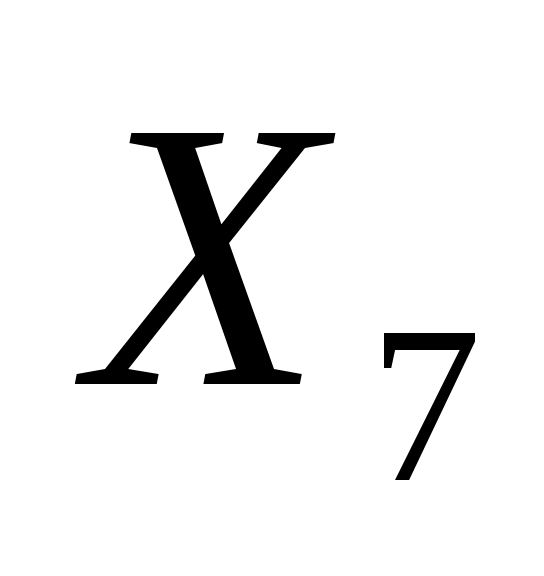 : 0/5,87=0; : 0/5,87=0; 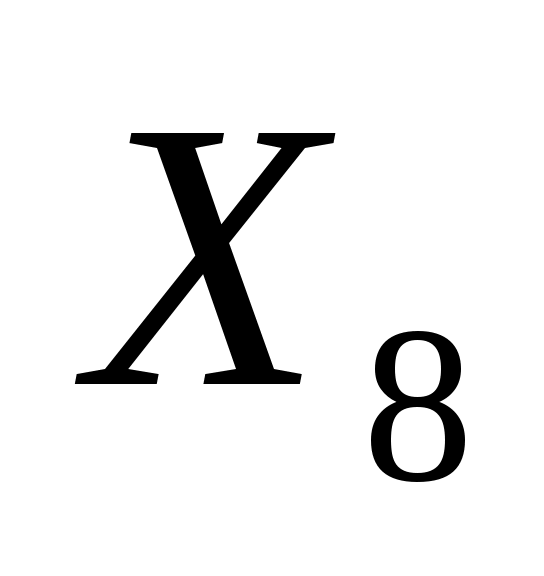 : 100000/9=11111; значит, ведущая строка соответствует переменной : 100000/9=11111; значит, ведущая строка соответствует переменной 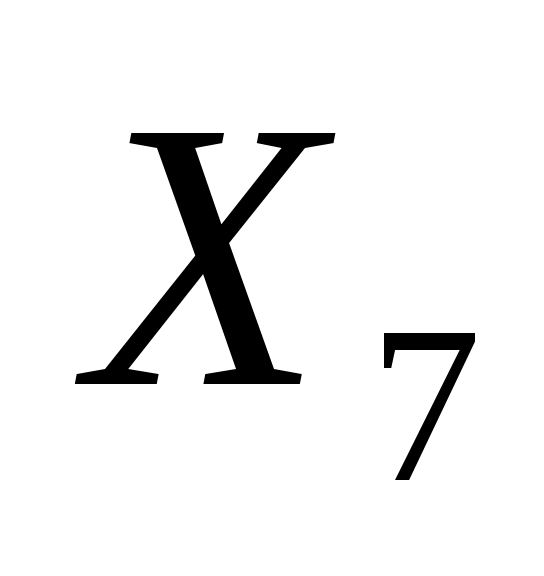 . Ведущий элемент равен 5,87. Выполнив преобразований по правилам симплекс-метода, получим новую симплекс-таблицу: . Ведущий элемент равен 5,87. Выполнив преобразований по правилам симплекс-метода, получим новую симплекс-таблицу:
Таблица 4.3 – симплекс- таблица №3
БП
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
X8
|
X9
|
БР
|
E
|
0
|
-3300
|
0
|
-6950
|
-12078
|
0
|
16448
|
0
|
0
|
0
|
X3
|
0
|
0
|
1
|
0
|
-0,46
|
0
|
1,62
|
0
|
0
|
0
|
X6
|
0
|
-0,77
|
0
|
0,13
|
0
|
1
|
0
|
0
|
0
|
0
|
X1
|
1
|
0
|
0
|
0
|
-1,28
|
0
|
0,17
|
0
|
0
|
0
|
X8
|
0
|
0
|
0
|
0
|
1,55
|
0
|
-1,53
|
1
|
0
|
100000
|
X9
|
0
|
0,9
|
0
|
0,85
|
0
|
0
|
0
|
0
|
1
|
120000
|
Полученное решение не является оптимальным: в строке целевой функции имеется отрицательные элементы. Решение продолжается. Ведущий столбец соответствует переменной 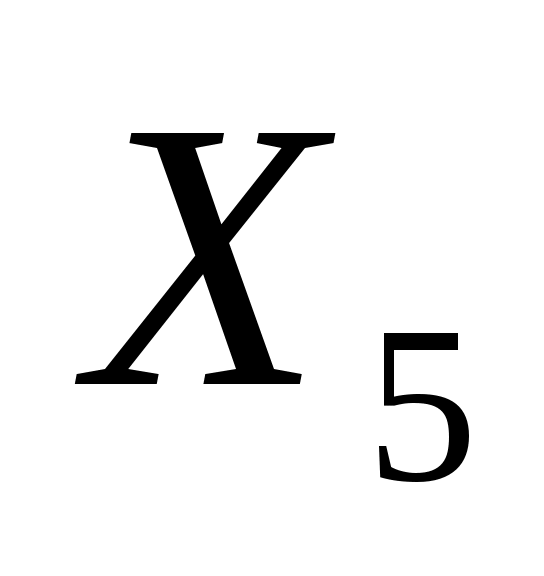 , у нее максимальный по модулю отрицательный коэффициент в строке целевой функции. Симплексные отношения: , у нее максимальный по модулю отрицательный коэффициент в строке целевой функции. Симплексные отношения:
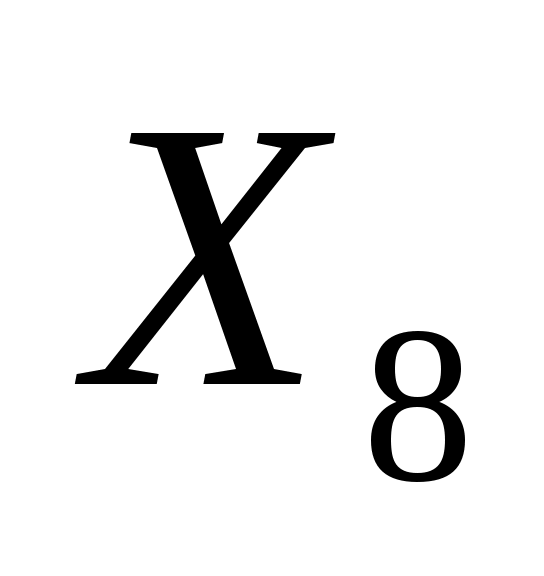 : 100000/1,55=64516; ведущая строка соответствует переменной : 100000/1,55=64516; ведущая строка соответствует переменной 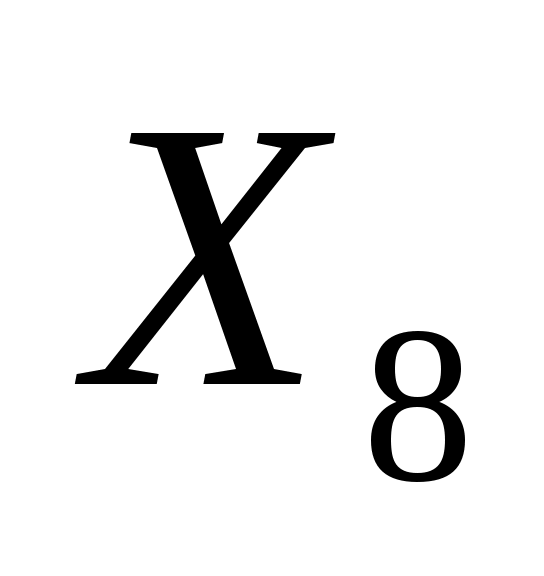 . Ведущий элемент равен 1,55. Выполнив преобразований по правилам симплекс-метода, получим новую симплекс-таблицу: . Ведущий элемент равен 1,55. Выполнив преобразований по правилам симплекс-метода, получим новую симплекс-таблицу:
Таблица 4.4 – симплекс- таблица №4
БП
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
X8
|
X9
|
БР
|
E
|
0
|
-3300
|
0
|
-6950
|
0
|
0
|
4471,8
|
7809
|
0
|
780946208
|
X3
|
0
|
0
|
1
|
0
|
0
|
0
|
1,17
|
0,3
|
0
|
29812,05
|
X6
|
0
|
-0,77
|
0
|
0,13
|
0
|
1
|
0
|
0
|
0
|
0
|
X1
|
1
|
0
|
0
|
0
|
0
|
0
|
-1,1
|
0,83
|
0
|
82955,28
|
X5
|
0
|
0
|
0
|
0
|
1
|
0
|
-0,99
|
0,65
|
0
|
64659,75
|
X9
|
0
|
0,9
|
0
|
0,85
|
0
|
0
|
0
|
0
|
1
|
120000
|
Полученное решение не является оптимальным: в строке целевой функции имеется отрицательные элементы. Решение продолжается. Ведущий столбец соответствует переменной 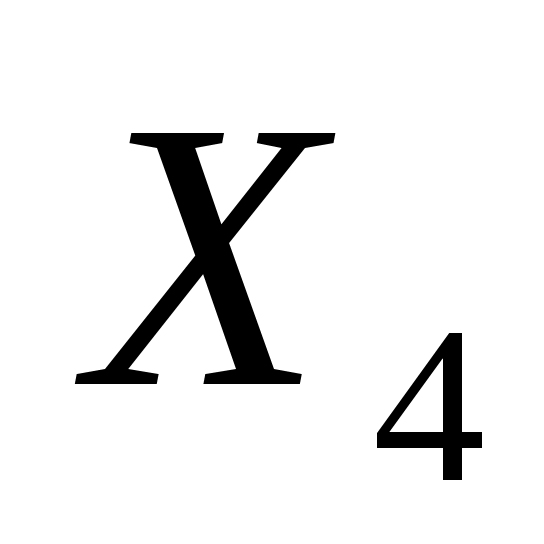 , у нее максимальный по модулю отрицательный коэффициент в строке целевой функции. Симплексные отношения: , у нее максимальный по модулю отрицательный коэффициент в строке целевой функции. Симплексные отношения:
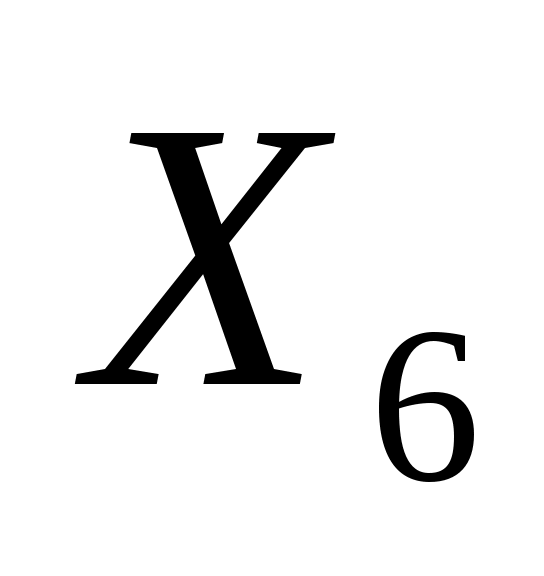 : 0/0,13=0; : 0/0,13=0; 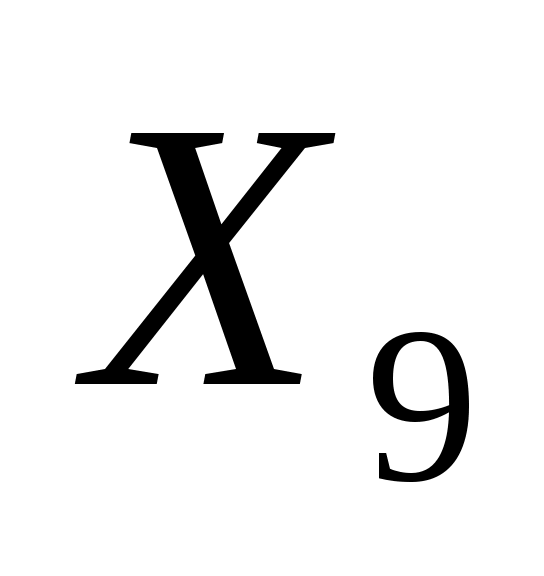 : 120000/0,85=141176; ведущая строка соответствует переменной : 120000/0,85=141176; ведущая строка соответствует переменной 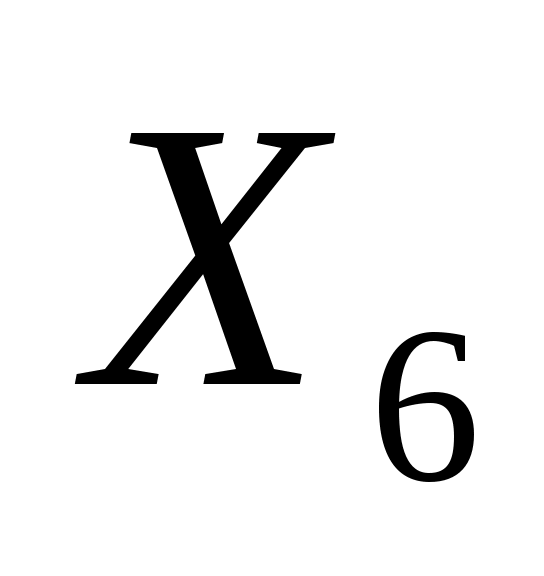 . Ведущий элемент равен 0,13. Выполнив преобразований по правилам симплекс-метода, получим новую симплекс-таблицу: . Ведущий элемент равен 0,13. Выполнив преобразований по правилам симплекс-метода, получим новую симплекс-таблицу:
Таблица 4.5 – симплекс- таблица №5
БП
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
X8
|
X9
|
БР
|
E
|
0
|
-44465
|
0
|
0
|
0
|
53462
|
4471,8
|
7809
|
0
|
780946209
|
X3
|
0
|
0
|
1
|
0
|
0
|
0
|
1,17
|
0,3
|
0
|
29812,05
|
X4
|
0
|
-5,92
|
0
|
1
|
0
|
7,69
|
0
|
0
|
0
|
0
|
X1
|
1
|
0
|
0
|
0
|
0
|
0
|
-1,1
|
0,83
|
0
|
82955,28
|
X5
|
0
|
0
|
0
|
0
|
1
|
0
|
-0,99
|
0,65
|
0
|
64659,75
|
X9
|
0
|
5,93
|
0
|
0
|
0
|
-6,54
|
0
|
0
|
1
|
120000
|
Полученное решение не является оптимальным: в строке целевой функции имеется отрицательные элемент. Решение продолжается. Ведущий столбец соответствует переменной 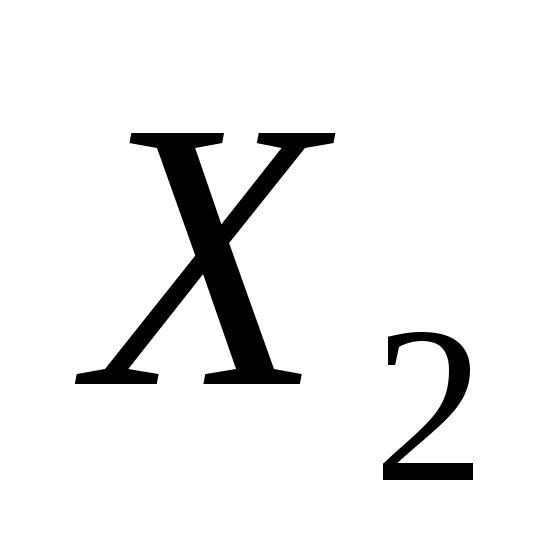 , так как только для этой переменной в E-строке содержится отрицательный элемент. Симплексные отношения: , так как только для этой переменной в E-строке содержится отрицательный элемент. Симплексные отношения:
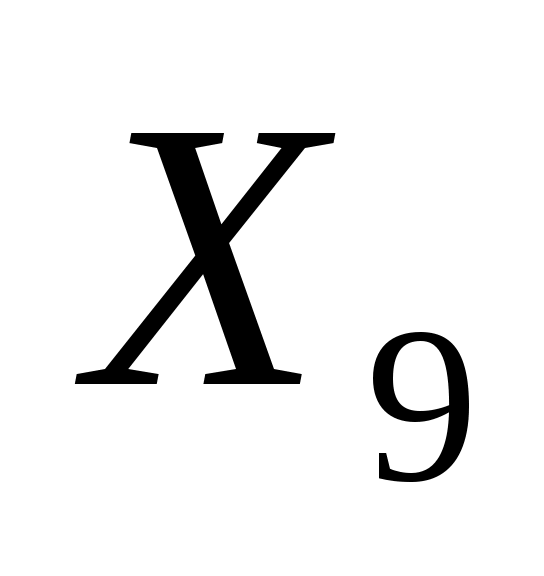 : 120000/5,93=20236; ведущая строка соответствует переменной : 120000/5,93=20236; ведущая строка соответствует переменной 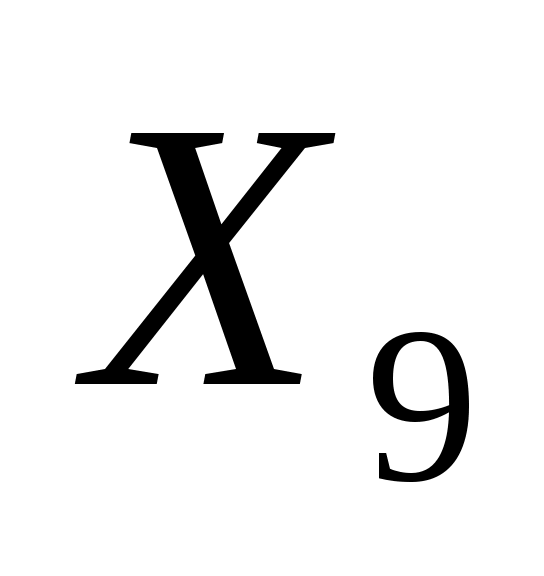 . Ведущий элемент равен 5,93. Выполнив преобразований по правилам симплекс-метода, получим новую симплекс-таблицу: . Ведущий элемент равен 5,93. Выполнив преобразований по правилам симплекс-метода, получим новую симплекс-таблицу:
Таблица 4.6 – симплекс- таблица №6
БП
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
X8
|
X9
|
БР
|
E
|
0
|
0
|
0
|
0
|
0
|
4472
|
4472
|
7809
|
7493
|
1680051847
|
X3
|
0
|
0
|
1
|
0
|
0
|
0
|
1,17
|
0,3
|
0
|
29812
|
X4
|
0
|
0
|
0
|
1
|
0
|
1,17
|
0
|
0
|
1
|
119767
|
X1
|
1
|
0
|
0
|
0
|
0
|
0
|
-1,1
|
0,83
|
0
|
82955
|
X5
|
0
|
0
|
0
|
0
|
1
|
0
|
-0,99
|
0,65
|
0
|
64660
|
X2
|
0
|
1
|
0
|
0
|
0
|
-1,1
|
0
|
0
|
0,17
|
20220
|
Все элементы Е-строки положительные, значит оптимальное решение найдено. Основные переменные задачи приняли следующие значения:
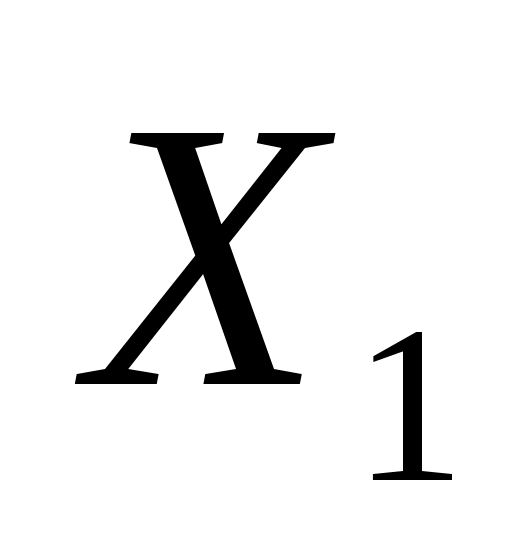 =82955 – количество тонн нефти компании “Севернефть” купленной для изготовления смазочного материал “Люкс” =82955 – количество тонн нефти компании “Севернефть” купленной для изготовления смазочного материал “Люкс”
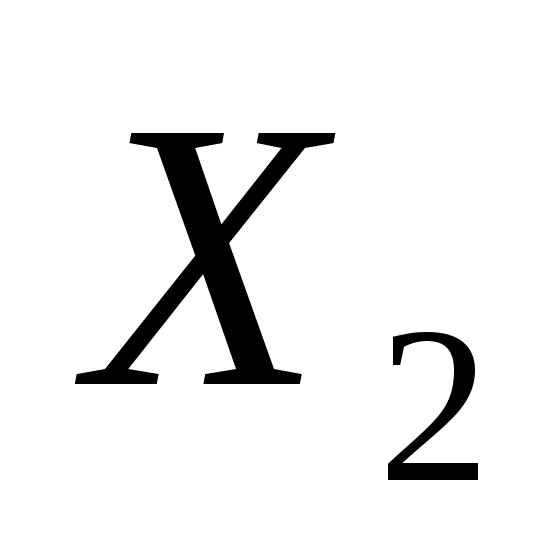 =20220 – количество тонн нефти компании “Севернефть” купленной для изготовления смазочного материал “Стандарт” =20220 – количество тонн нефти компании “Севернефть” купленной для изготовления смазочного материал “Стандарт”
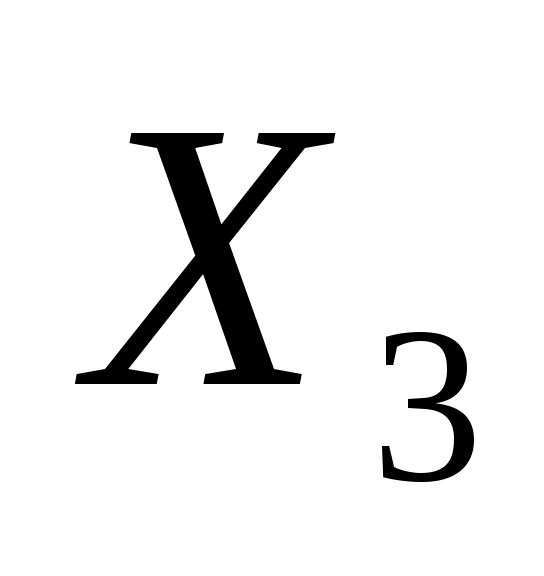 =29812 – количество тонн нефти компании “Афройл” купленной для изготовления смазочного материал “Люкс” =29812 – количество тонн нефти компании “Афройл” купленной для изготовления смазочного материал “Люкс”
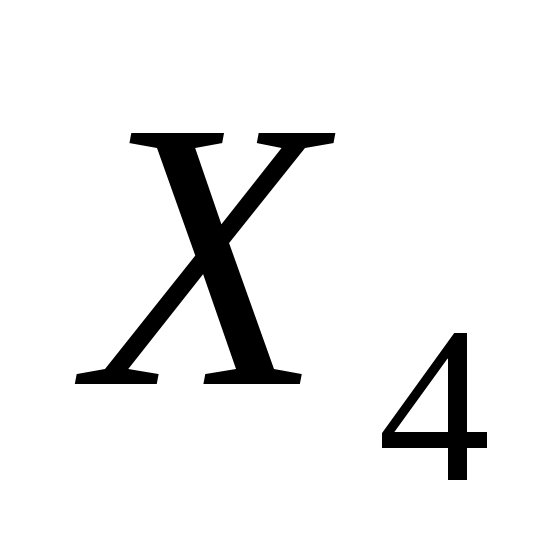 =119767 – количество тонн нефти компании “Афройл” купленной для изготовления смазочного материал “Стандарт” =119767 – количество тонн нефти компании “Афройл” купленной для изготовления смазочного материал “Стандарт”
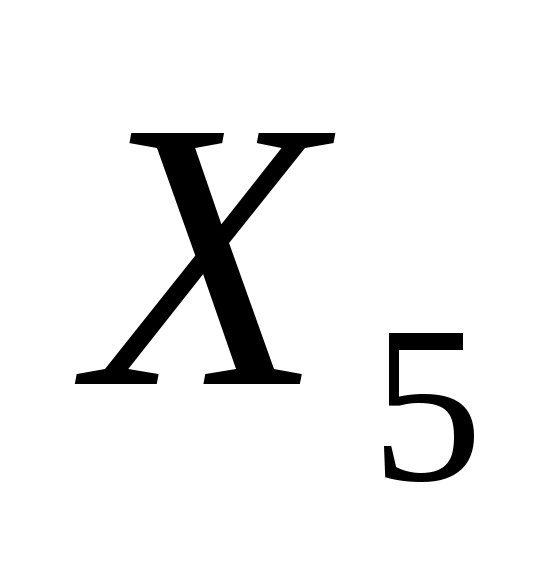 =64660 – в смазочном материале “Люкс” будет содержаться на 64660 тонн нефти компании “Севернефть” свыше установленного минимума. =64660 – в смазочном материале “Люкс” будет содержаться на 64660 тонн нефти компании “Севернефть” свыше установленного минимума.
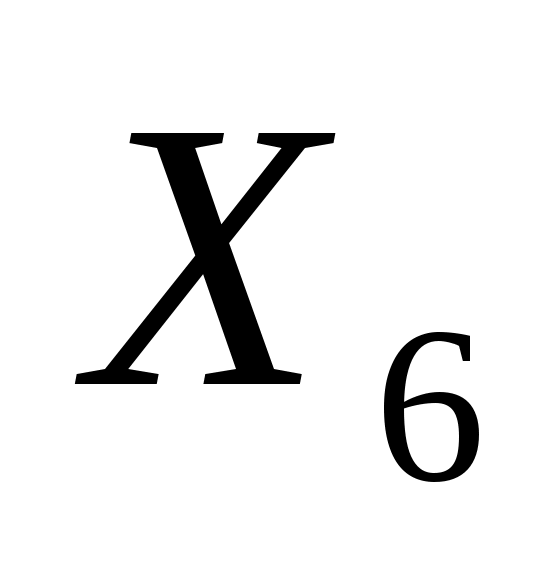 =0 – количество тонн нефти компании “Севернефть” содержащееся в смазочном материале “Стандарт” сверх установленного минимума. Ее равенство нулю означает, что в смазочном материала “Стандарт” содержание нефти компании “Севернефть” не превысит установленный минимум в 15%. =0 – количество тонн нефти компании “Севернефть” содержащееся в смазочном материале “Стандарт” сверх установленного минимума. Ее равенство нулю означает, что в смазочном материала “Стандарт” содержание нефти компании “Севернефть” не превысит установленный минимум в 15%.
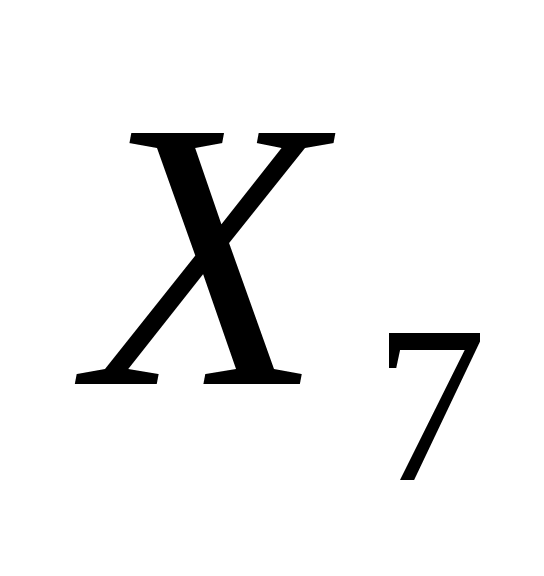 =0 – количество тонн нефти компании “Афройл”, которое можно было бы еще добавить в смазочный материал “Люкс”, не нарушив при этом ограничение на процентное содержание данного вида нефти в данном смазочном материале. Т.к. значение переменной равно нулю, то это означает что в смазочном материале “Люкс” содержится ровно 25% нефти компании “Афройл”. =0 – количество тонн нефти компании “Афройл”, которое можно было бы еще добавить в смазочный материал “Люкс”, не нарушив при этом ограничение на процентное содержание данного вида нефти в данном смазочном материале. Т.к. значение переменной равно нулю, то это означает что в смазочном материале “Люкс” содержится ровно 25% нефти компании “Афройл”.
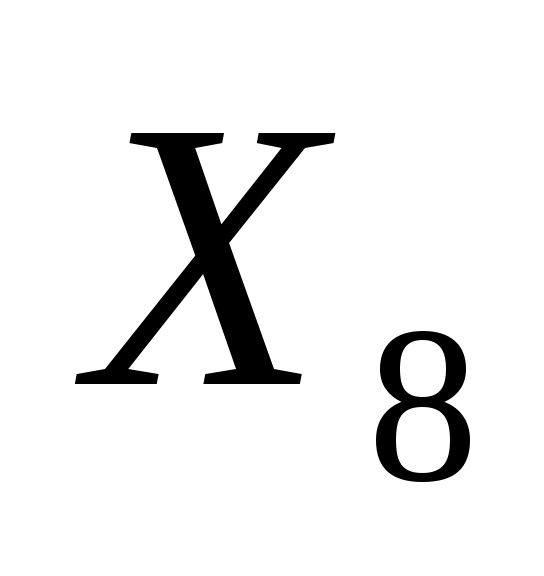 =0 – невостребованная квота на продажу смазочного материала “Люкс”. Равенство данной переменной нулю означает, что продано ровно 100000 тонн данного вида смазочного материала. =0 – невостребованная квота на продажу смазочного материала “Люкс”. Равенство данной переменной нулю означает, что продано ровно 100000 тонн данного вида смазочного материала.
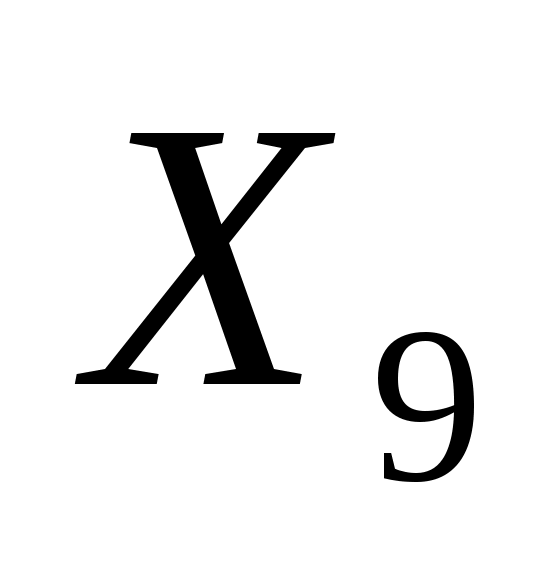 =0 – невостребованная квота на продажу смазочного материала “Стандарт”. Равенство данной переменной нулю означает, что продано ровно 120000 тонн данного вида смазочного материала. =0 – невостребованная квота на продажу смазочного материала “Стандарт”. Равенство данной переменной нулю означает, что продано ровно 120000 тонн данного вида смазочного материала.
Таким образом, при изготовлении смазочный материал “Люкс” будет содержать: 75% нефти компании “Севернефть” и 25% нефти компании “Афройл”. Смазочный материал “Стандарт” будет содержать: 15% нефти компании “Севернефть” и 85% нефти компании “Афройл”.
Прибыль от продажи смазочных материалов составит 1680051847 ден. ед.
Протокол решения оптимизационной задачи с использованием пакета SIMPLEX-M в Приложении А.
|
 Скачать 0.98 Mb.
Скачать 0.98 Mb.