Домашка по кудьтуре речи. "Функции нескольких переменных"
 Скачать 1.29 Mb. Скачать 1.29 Mb.
|
|
ТИПОВОЙ РАСЧЕТ по теме “Функции нескольких переменных” Вариант №1 Для заданной функции найти все частные производные первого порядка: а) 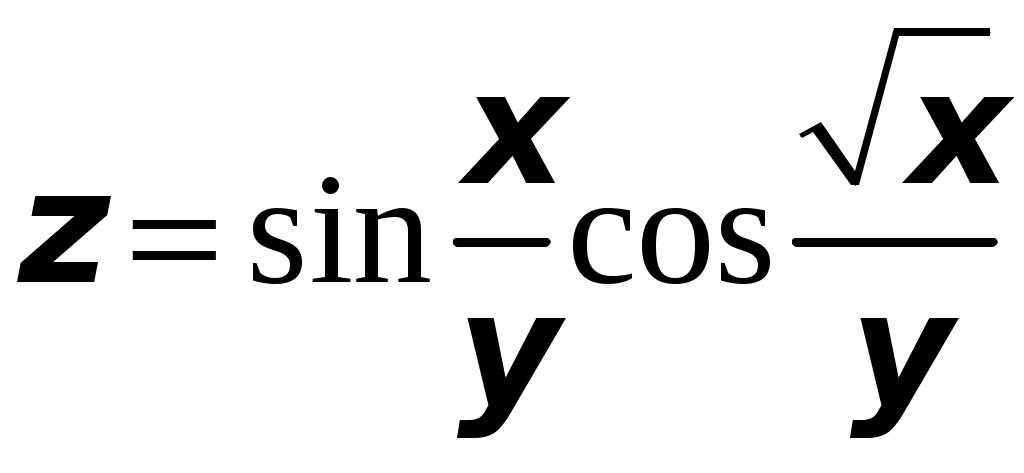 ; б) ; б) Для заданной функции найти требуемые частные и смешанные производные:  Найти производные неявно заданной функции: а) 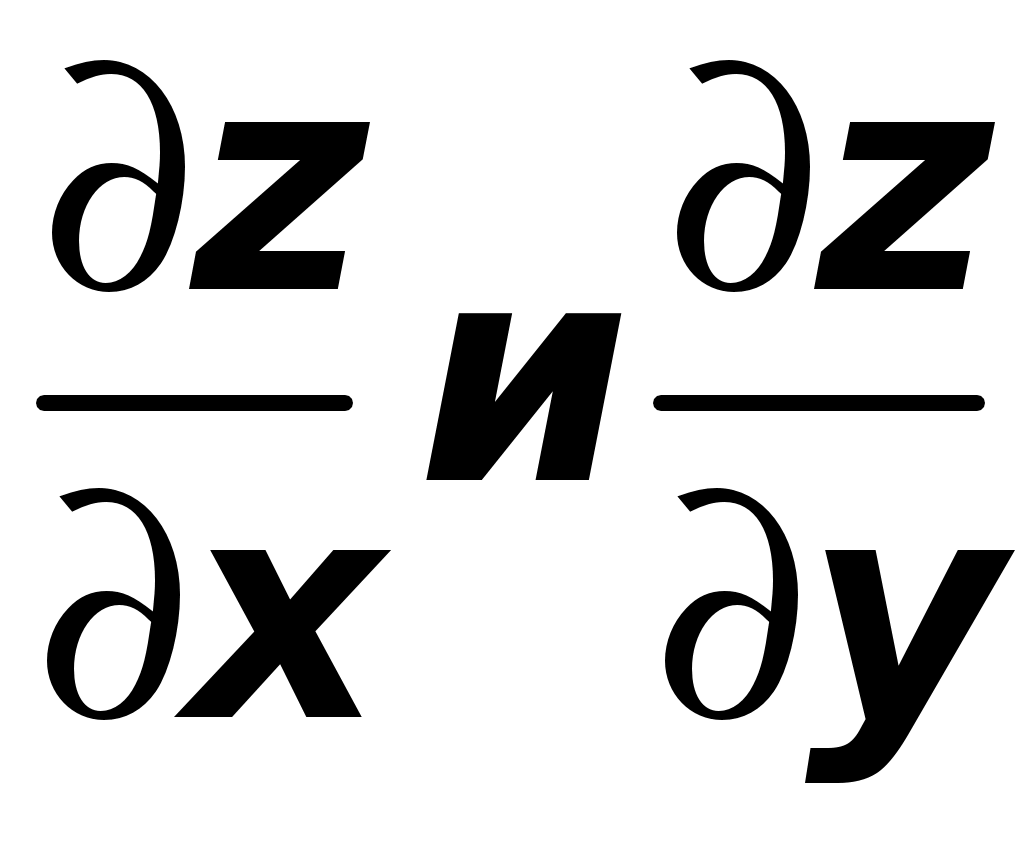 ; б) ; б) 1. Найти градиент функции Для функции С помощью полного дифференциала найти приближенное значение функции: Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке Исследовать на экстремум функцию ТИПОВОЙ РАСЧЕТ по теме “Функции нескольких переменных” Вариант №2 Для заданной функции найти все частные производные первого порядка: а) Для заданной функции найти требуемые частные и смешанные производные: 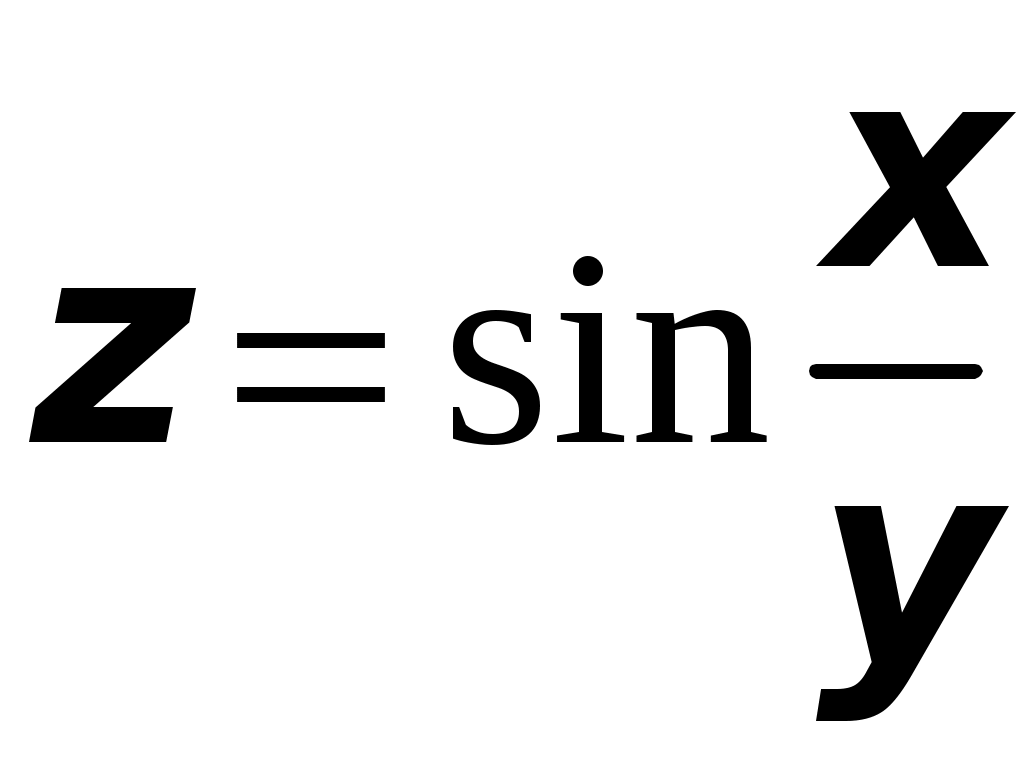 ; ; 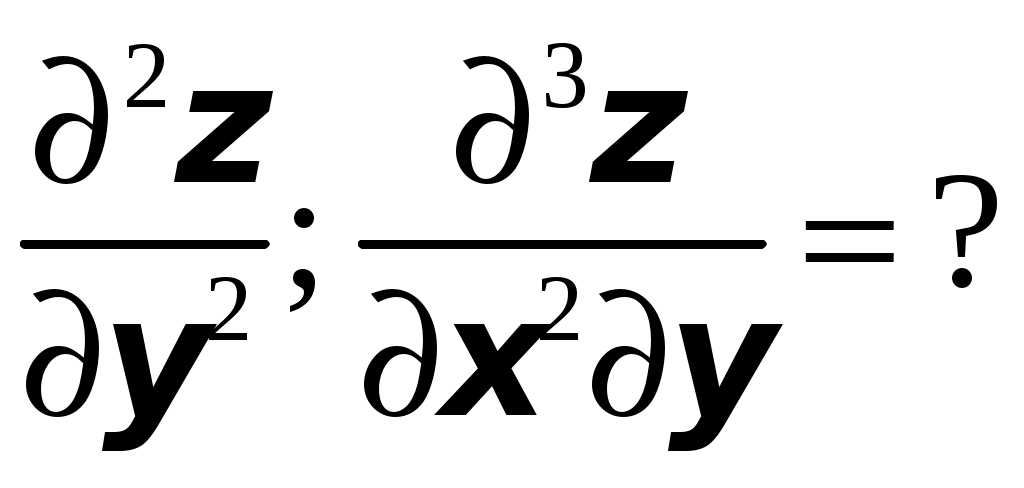 Найти производные неявно заданной функции: а) 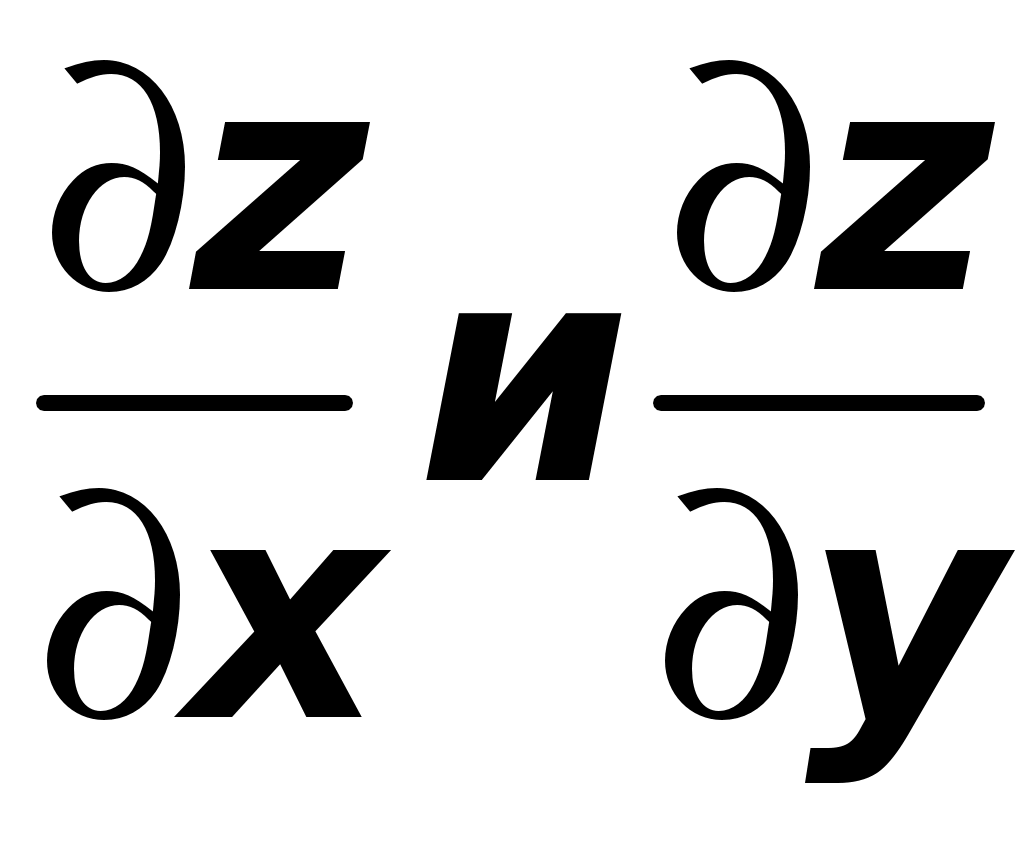 ; б) ; б) 1. Найти градиент функции Для функции 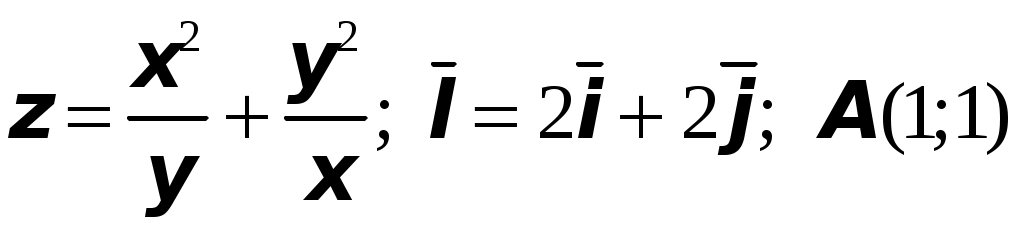 С помощью полного дифференциала найти приближенное значение функции: Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке Исследовать на экстремум функцию ТИПОВОЙ РАСЧЕТ по теме “Функции нескольких переменных” Вариант №3 Для заданной функции найти все частные производные первого порядка: а) 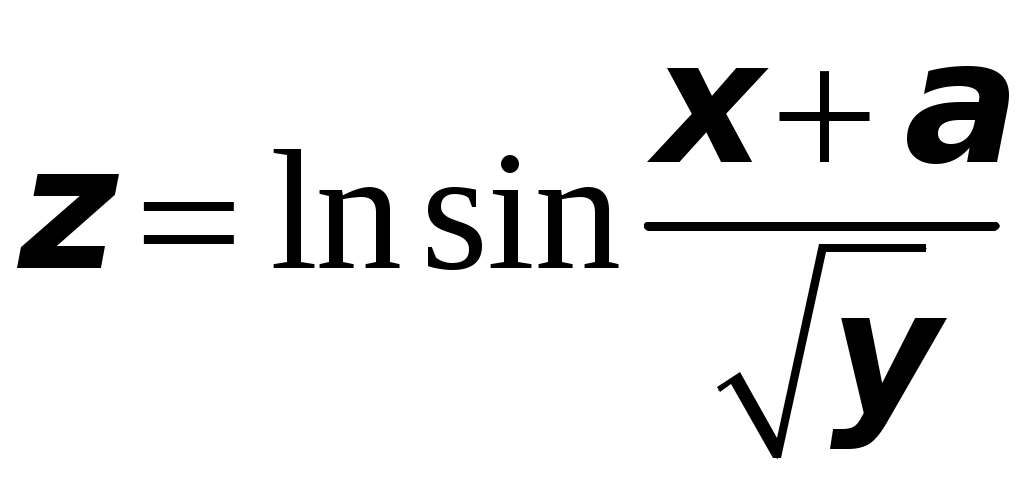 ; б) ; б) Для заданной функции найти требуемые частные и смешанные производные: 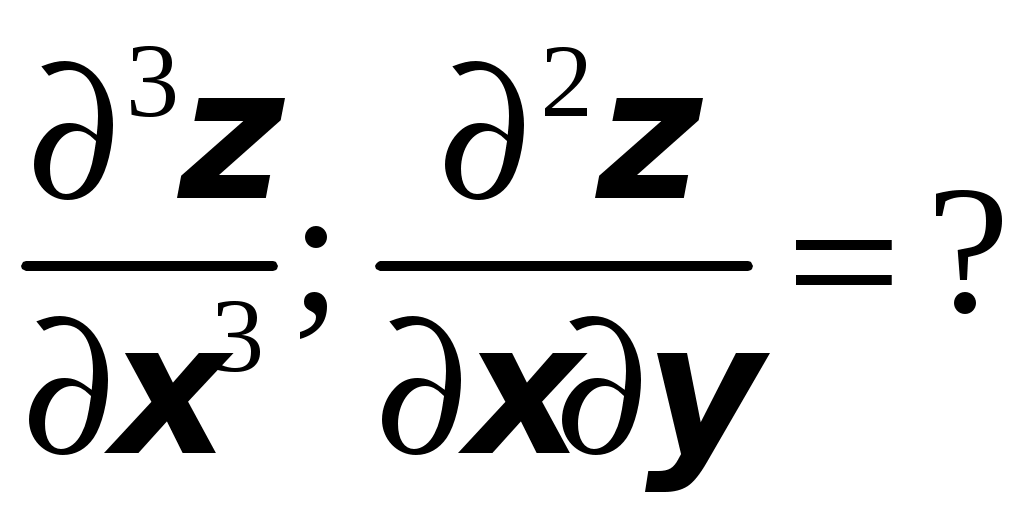 Найти производные неявно заданной функции: а) 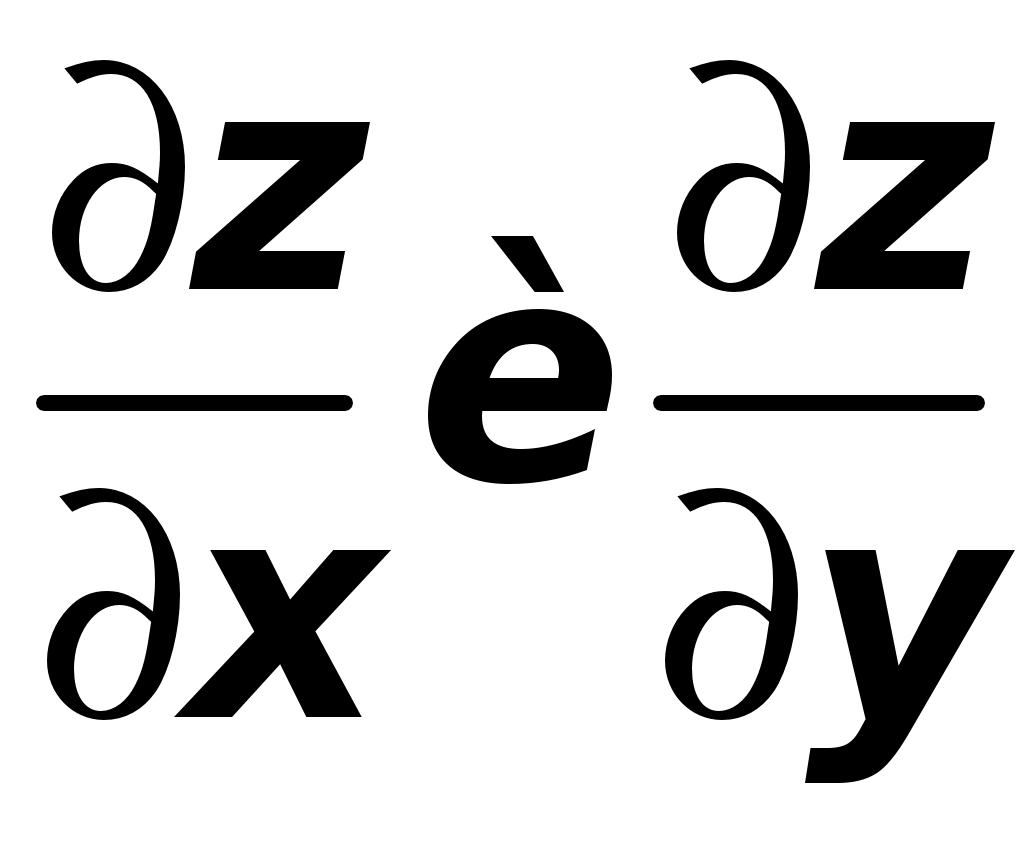 ; б) ; б) 1. Найти градиент функции Для функции С помощью полного дифференциала найти приближенное значение функции: Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке Исследовать на экстремум функцию 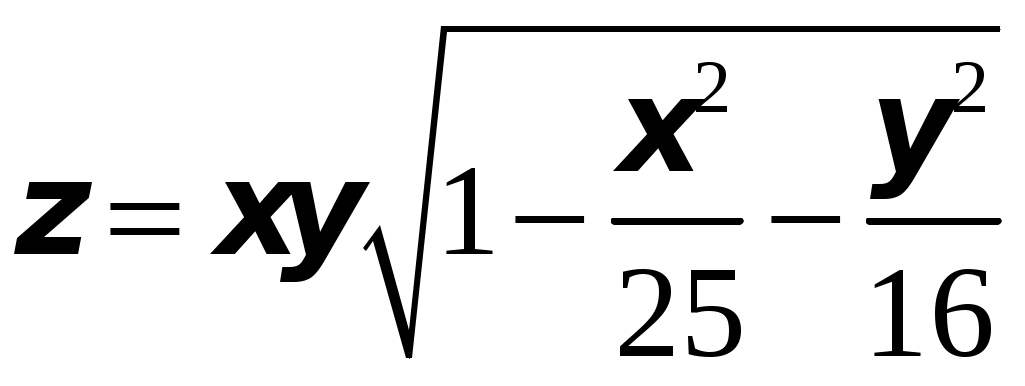 ТИПОВОЙ РАСЧЕТ по теме “Функции нескольких переменных” Вариант №4 Для заданной функции найти все частные производные первого порядка: а) 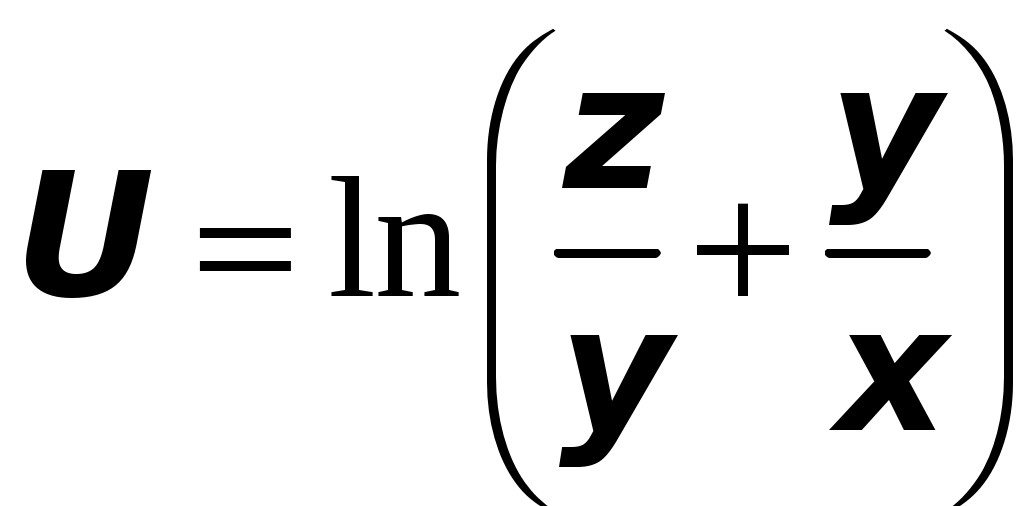 ; ; Для заданной функции найти требуемые частные и смешанные производные: 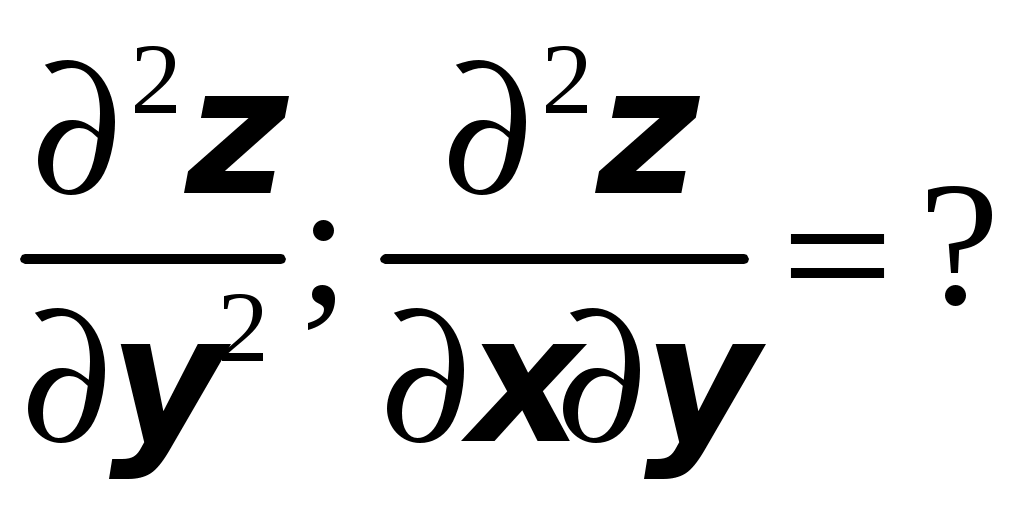 Найти производные неявно заданной функции: а) 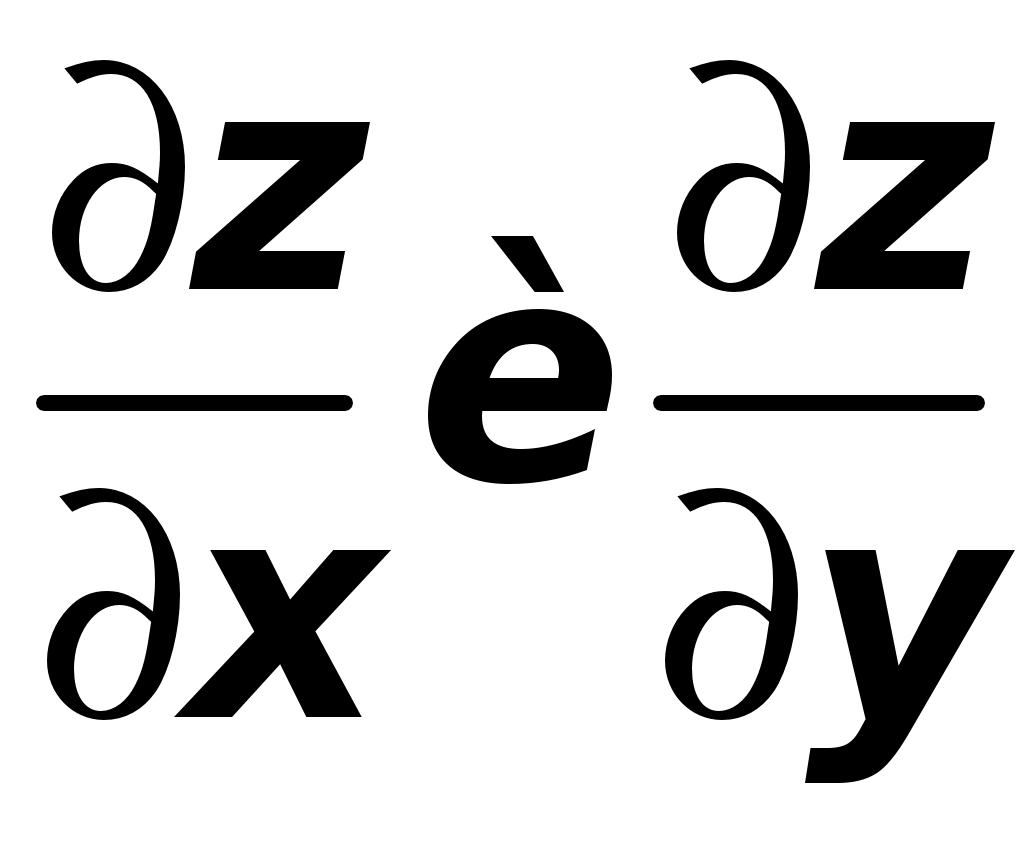 ; б) ; б) 1. Найти градиент функции Для функции С помощью полного дифференциала найти приближенное значение функции: 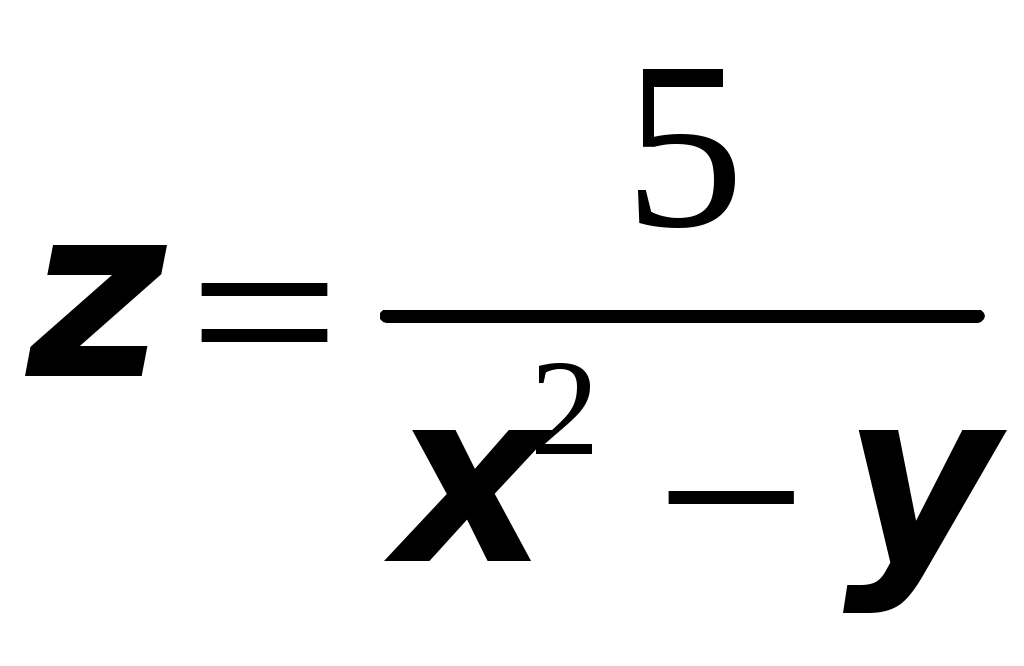 при при Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке Исследовать на экстремум функцию ТИПОВОЙ РАСЧЕТ по теме “Функции нескольких переменных” Вариант №5 Для заданной функции найти все частные производные первого порядка: а) Для заданной функции найти требуемые частные и смешанные производные: 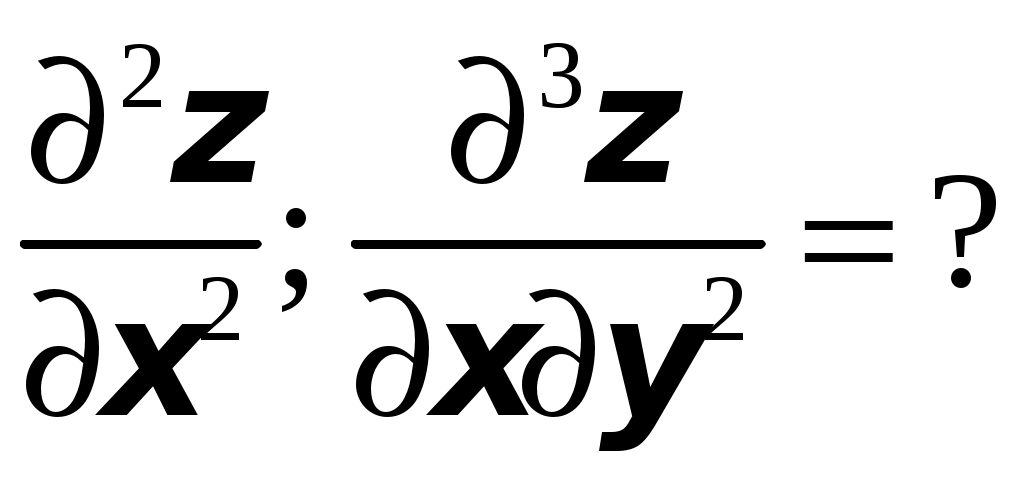 Найти производные неявно заданной функции: а) 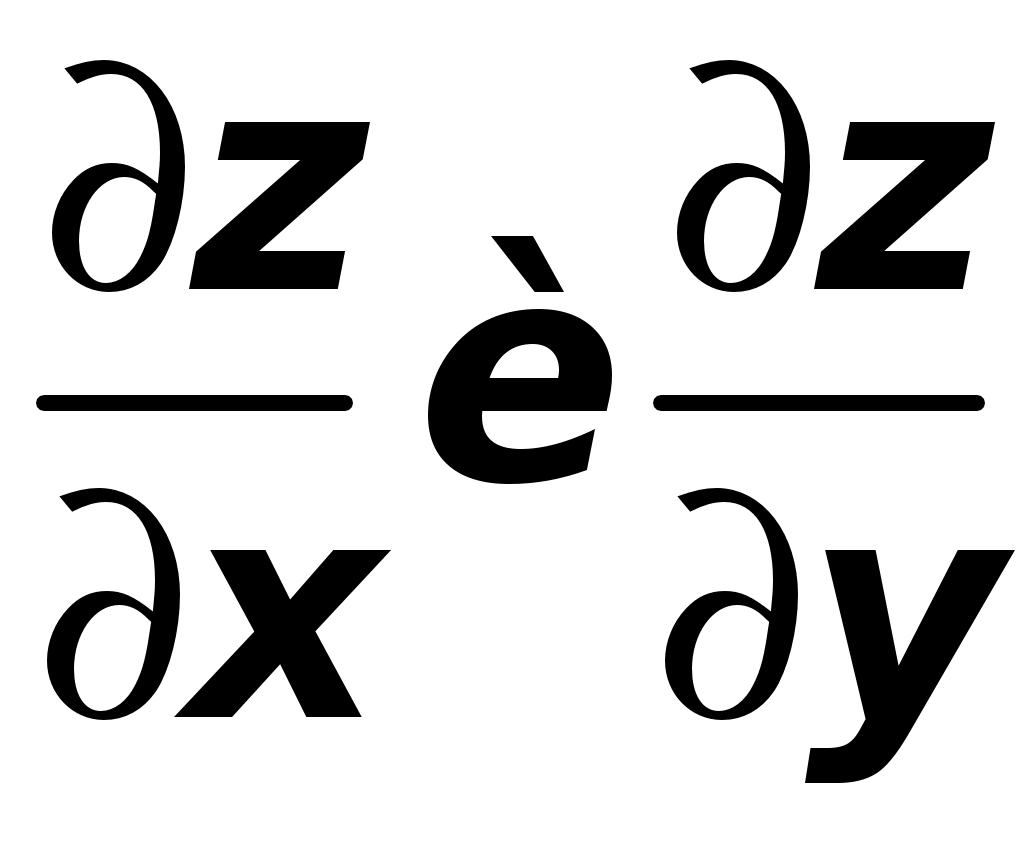 ; б) ; б) 1. Найти градиент функции Для функции С помощью полного дифференциала найти приближенное значение функции: Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке Исследовать на экстремум функцию ТИПОВОЙ РАСЧЕТ по теме “Функции нескольких переменных” Вариант №6 Для заданной функции найти все частные производные первого порядка: а) Для заданной функции найти требуемые частные и смешанные производные: 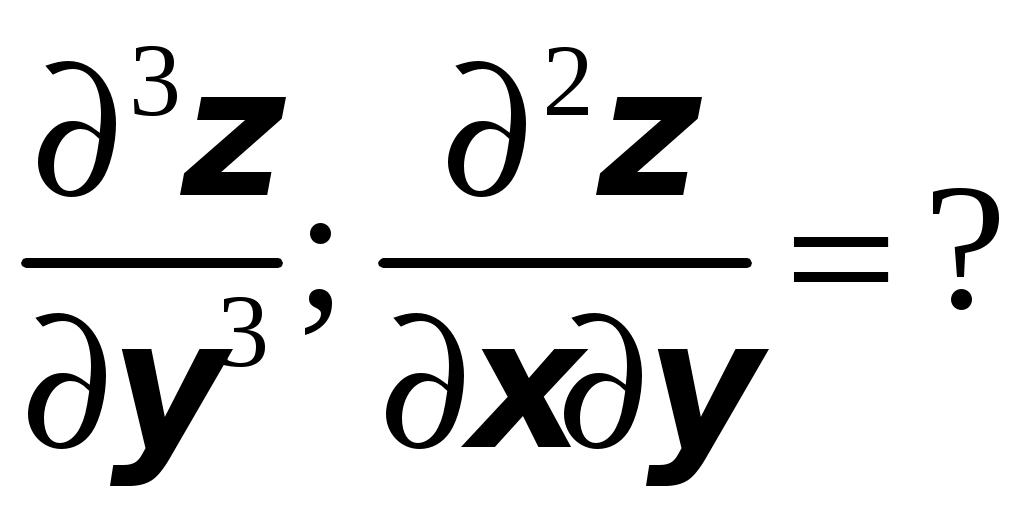 Найти производные неявно заданной функции: а) 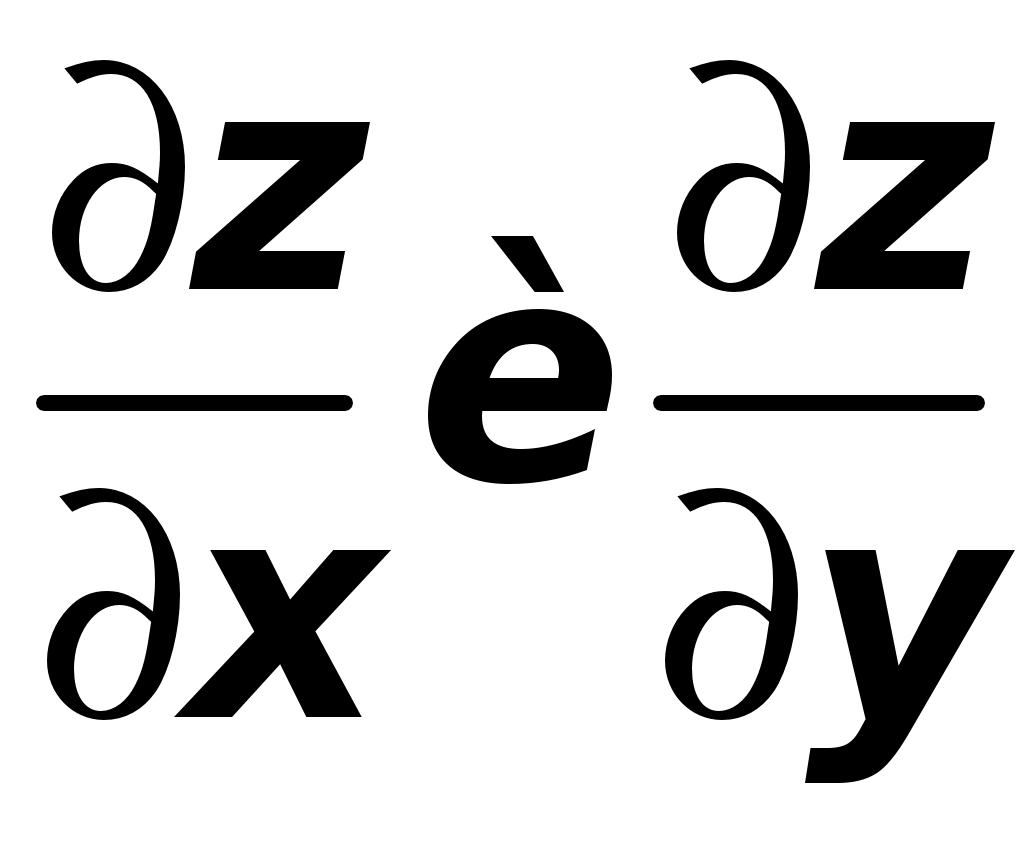 ; б) ; б) 1. 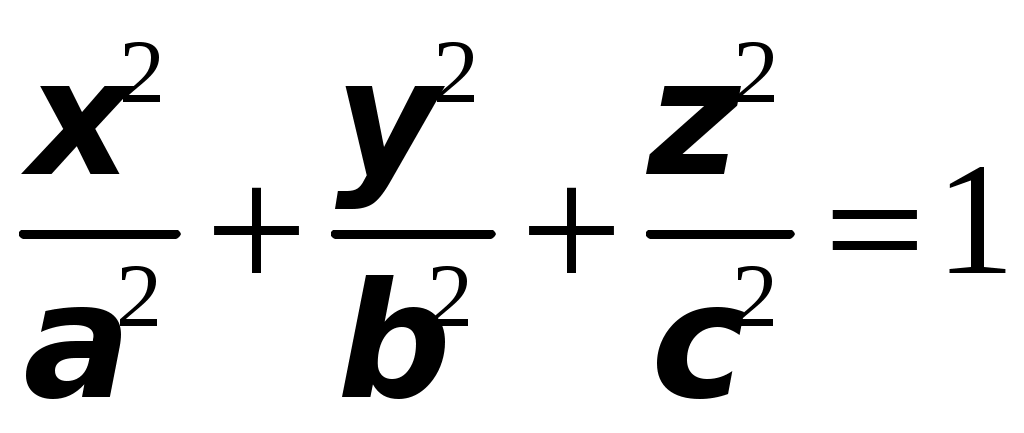 ; 2. ; 2. 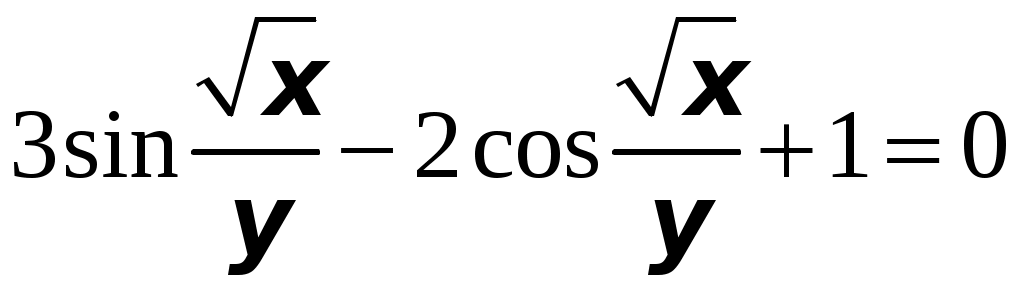 Найти градиент функции Для функции С помощью полного дифференциала найти приближенное значение функции: Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке Исследовать на экстремум функцию ТИПОВОЙ РАСЧЕТ по теме “Функции нескольких переменных” Вариант |
