Комплексное. Функция ysin(x). Свойства, график
 Скачать 91.73 Kb. Скачать 91.73 Kb.
|
|
Функция y=sin(x). Свойства, график. Зависимость, при которой каждому действительному числу х соответствует значение sinx называется функцией y=sinx. Функция y=sinx Область определения: D(x)=R y(-x)=-y(x)-нечетная Период: T=2π. Построение графика этой функции происходит таким же способом, как и графика функции y=cosx, начиная с построения, например, на отрезке [0; π.] Но можно упростить, применив формулу sinx=cos( x- 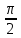 ), которая показывает, что график функции y=sinx можно получить путем сдвига графика функции y=cosx вдоль оси абсцисс вправо на ), которая показывает, что график функции y=sinx можно получить путем сдвига графика функции y=cosx вдоль оси абсцисс вправо на 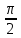 . .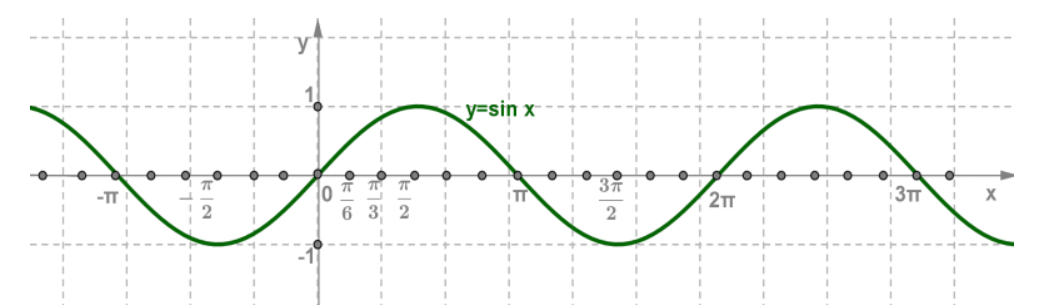 График функции y=sinx Кривая, являющаяся графиком функции y=sinx, называется синусоидной. СВОЙСТВА ФУНКЦИИ y=sinx 1. Область определения – множество R всех действительных чисел. 2. Множество значений – отрезок [-1;1]. 3. Функция y=sinx имеет период T=2π. 4. Функция y=sinx является нечетной. 5. Нули функции: x= πn, n∈Z; Наибольшее значение равно 1 при х= 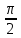 +2πn, n∈Z; +2πn, n∈Z;Наименьшее значение равно -1 при х=- 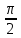 +2πn, n∈Z; +2πn, n∈Z;Значения функции положительны на интервале (0; π), с учетом периодичности функции на интервалах (2 πn; π+2πn), n∈Z; Значения функции отрицательны на интервале (π; 2π; 2π+2πn), n∈Z. 6. Функция y=sinx: -возрастает на отрезке [- 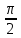 ; ; 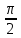 ], с учетом периодичности функции на отрезках ], с учетом периодичности функции на отрезках[- 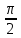 +2πn; +2πn; 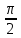 +2πn], n∈Z; +2πn], n∈Z;-убывает на отрезке [ 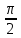 ; ; 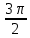 ], с учетом периодичности функции на отрезках [ ], с учетом периодичности функции на отрезках [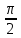 +2πn; +2πn; 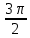 +2πn], n∈Z. +2πn], n∈Z. |
