Гармонические колебания. Гармонические колебания
 Скачать 395.62 Kb. Скачать 395.62 Kb.
|
|
Урок № ________ Дата_________ Тема: Гармонические колебания. Цель урока: Освоение учащимися знаний о гармонических колебаний на основе межпредметных связей естественно-научного и математического циклов предметов. Задачи урока: Формирование исследовательского умения через извлечение информации из графика и уравнений зависимостей координаты, скорости и ускорения от времени. Способствовать развитию умения анализировать, обобщать, делать выводы, развитию логического мышления; Продолжить формирование научного мировоззрения, способности к организации индивидуальной и коллективной учебной работы. Тип урока: урок формирования новых знаний Ход урока Организационный момент. Проверка домашнего задания. Фронтальный опрос. - Что такое механические колебания? - Какие виды колебаний вы знаете? - Какие колебания называют свободными? - Какие условия необходимы для возникновения свободных колебаний? - Какие колебания называются вынужденными? - Перечислите основные кинематические характеристики колебательного движения. Какие из перечисленных колебаний являются свободными или вынужденными: колебания листьев на деревьях во время ветра; биение сердца; колебания качелей; колебание груза на пружине; колебание струны после того, как её выведут из положения равновесия; колебания поршня в цилиндре; колебание шарика на нити; колебание травы в поле на ветру колебание голосовых связок. Изучение нового материала. Простейшим видом колебаний являются гармонические колебания. Термин «гармонические колебания» впервые был введен в науку швейцарским физиком Даниилом Бернулли. Г 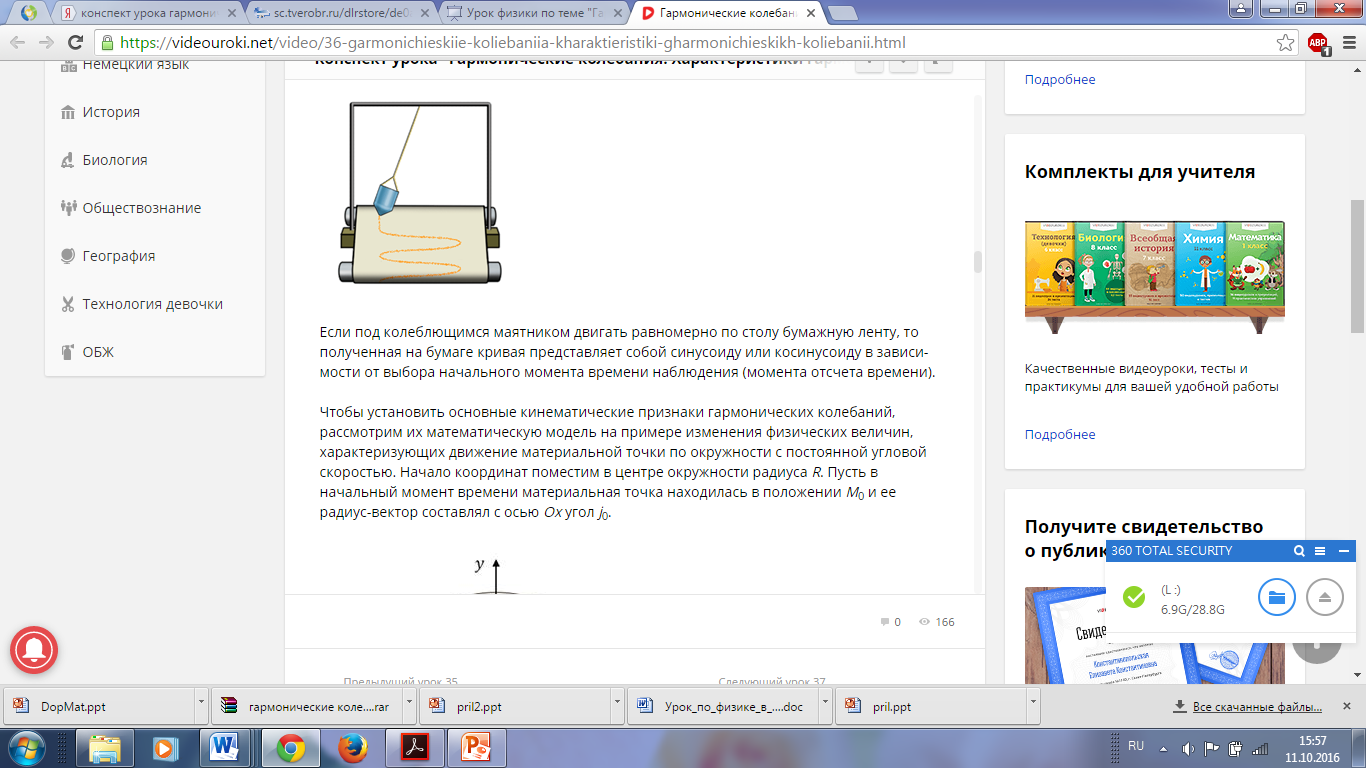 армоническими называются колебания, при которых какая-либо величина изменяется с течением времени по закону синуса или косинуса. армоническими называются колебания, при которых какая-либо величина изменяется с течением времени по закону синуса или косинуса.Например, гармонические колебания физического маятника можно зарегистрировать следующим способом. В качестве груза взять небольшой стакан с песком, который может высыпаться через очень маленькое отверстие снизу. Если под колеблющимся маятником двигать равномерно по столу бумажную ленту, то полученная на бумаге кривая представляет собой синусоиду или косинусоиду в зависимости от выбора начального момента времени наблюдения. Таким образом, кинематический закон любого гармонического движения можно представить в виде: 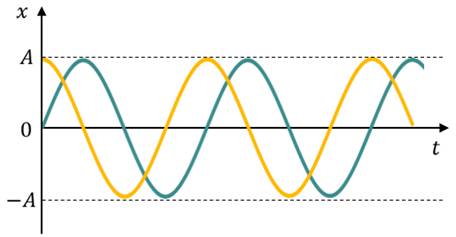 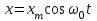 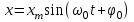 Следовательно, графически зависимость смещения колеблющейся точки от времени изображается косинусоидой или синусоидой. В записанных уравнениях 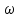 — это циклическая (или круговая) частота, которая показывает, сколько колебаний совершает материальная точка за 2π секунд. Соответственно, в системе СИ она измеряется в радианах на секунду. — это циклическая (или круговая) частота, которая показывает, сколько колебаний совершает материальная точка за 2π секунд. Соответственно, в системе СИ она измеряется в радианах на секунду.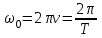 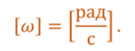 Рассмотрим, как изменяются проекции скорости и ускорения колеблющейся точки со временем для случая, когда начальная фаза колебаний равна нулю. 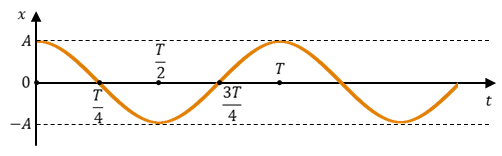 Скорость. Для этого найдем первую производную по времени от кинематического закона гармонических колебаний. 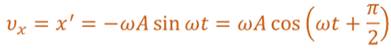 В полученном выражении произведение циклической частоты и амплитуды колебаний — это есть амплитуда проекции скорости на ось координат. Таким образом видим, что при гармонических колебаниях проекция скорости тела на координатную ось тоже изменяется по гармоническому закону с той же частотой, но с другой амплитудой и опережает по фазе смещение на π/2. 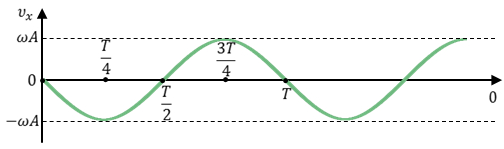 Теперь рассмотрим ускорение. Для этого найдем производную от проекции скорости по времени. Величина, равная произведению квадрата циклической частоты и амплитуды колебаний, является амплитудой проекции ускорения. Как видно из формулы, при гармонических колебаниях проекция ускорения опережает смещение по фазе на π. Говорят, что проекция ускорения изменяется с течением времени в противофазе изменению координаты. 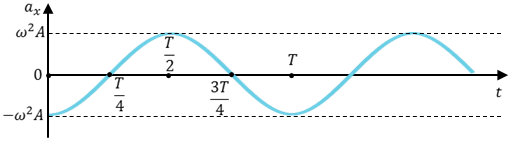 Учитывая кинематический закон гармонического движения получим, что при гармонических колебаниях проекция ускорения прямо пропорциональна смещению и противоположна ему по знаку, то есть направлено в сторону, противоположную смещению. При колебаниях периодически происходит переход потенциальной энергии в кинетическую и обратно. Полная механическая энергия такой колебательной системы равна сумме его кинетической и потенциальной энергий. 1. Уравнение колебательного движения груза на пружине С 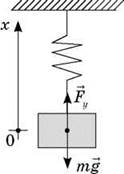 огласно второму закону Ньютона Fх = mах. Таким образом, уравнение, описывающее движение груза имеет вид: огласно второму закону Ньютона Fх = mах. Таким образом, уравнение, описывающее движение груза имеет вид: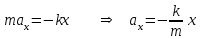 Обозначим. 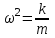 ( (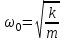 ). Тогда уравнение движения груза будет иметь вид: ). Тогда уравнение движения груза будет иметь вид: 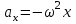 Уравнение такого вида называется дифференциальным уравнением. Решением этого уравнения является функция: 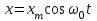 Величина 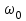 - циклическая или круговая частота колебаний. - циклическая или круговая частота колебаний. 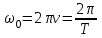 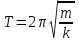 период малых колебаний пружинного маятника период малых колебаний пружинного маятника 2. Уравнение колебательного движения математического маятника. 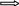 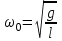 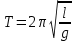 Работа с формулой. 1. Как изменится период колебаний математического маятника, если амплитуду его колебаний уменьшить в 2 раза? Трение отсутствует. 2. Как изменится период колебаний математического маятника, если длину нити увеличить в 4 раза? 3. Груз, прикреплённый к пружине, совершает гармонические колебания в горизонтальной плоскости. Как изменится период колебаний, если массу груза и жёсткость пружины увеличить в 2 раза? Вывод: Мы можем убедиться на опытах, что период колебаний математического маятника не зависит от массы груза и определяют его только длиной нити. Поскольку период колебаний математического маятника зависит от ускорения свободного падения g, то с помощью маятника можно делать точные измерения g. Известно, что в разных точках земного шара ускорение свободного падения разное. Оно зависит не только от формы Земли, но и от наличия в ее недрах тяжелых (металлы) или легких (газ, нефть) веществ. Итак, получается, что и период колебаний маятника в разных точках будет разный. Это свойство используют, в частности, для определения залежей полезных ископаемых. ФИЗМИНУТКА 3. Фаза колебаний. Величину 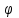 , стоящую под знаком функции косинуса или синуса, называется фазой колебаний. , стоящую под знаком функции косинуса или синуса, называется фазой колебаний.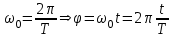 отношение отношение 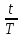 указывает, сколько периодов прошло от момента начала колебаний. Любому значению времени t , выраженному в числе периодов Т, соответствует значение фазы указывает, сколько периодов прошло от момента начала колебаний. Любому значению времени t , выраженному в числе периодов Т, соответствует значение фазы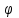 , выраженное в радианах. , выраженное в радианах.Синус отличается от косинуса сдвигом аргумента на 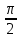 . .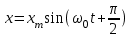 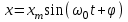 IV. Закрепление. Напишите уравнение гармонического колебания, если его амплитуда 0,5 м, а частота 25 Гц. Колебания груза на пружине описывают уравнением х = 0,1sin0,5 V. Итог урока. VI. Домашнее задание: § 22 - 24, № 427, 431 |
