йййй. Гармонический синтез сигналов
 Скачать 5.19 Mb. Скачать 5.19 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ТОР отчет по лабораторной работе № 2 по дисциплине «Радиотехнические цепи и сигналы» Тема: Гармонический синтез сигналов
Санкт-Петербург 2022 Цель работы – изучение процедуры синтеза периодических сигналов с помощью ограниченного числа гармонических колебаний. Основные теоретический положения Периодическое колебание прямоугольной формы (меандр) s1(t) имеет вид, изображенный на рис. 2.1, где τ = Т/2. Легко видеть, что в силу четности функции s1(t) и отсутствия постоянной составляющей ее разложение в ряд Фурье в форме будет содержать лишь косинусные компоненты, а именно: 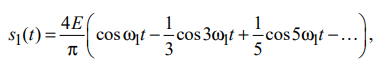 где Е – амплитуда меандра; ω1 = 2π/T – круговая частота первой гармоники. Периодическое колебание пилообразной формы s2(t) представлено на рис. 2.2. Оно, подобно предыдущему сигналу, не имеет постоянной составляющей и, в отличие от него, является нечетной функцией времени. 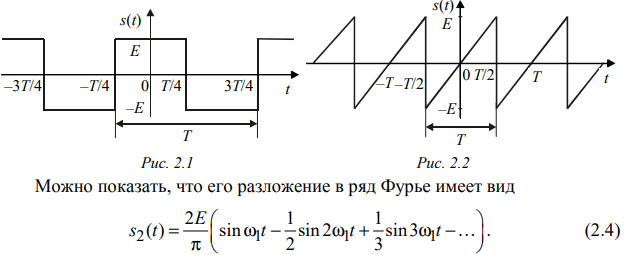 Периодическое колебание треугольной формы s3(t) изображено на рис. 2.3, особенности его представления рядом Фурье аналогичны случаю 1, а разложение таково: 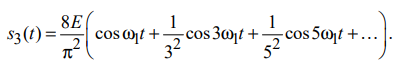 АМК с однотональной модуляцией s4(t) имеет следующее аналитическое выражение: где A0 , ω0 , ϕ0 – амплитуда, круговая частота и начальная фаза несущего колебания соответственно; 0 ≤ m ≤ 1 – коэффициент амплитудной модуляции; Ω, Ψ – круговая частота и начальная фаза модулирующего гармонического колебания. В частном случае при нулевых значениях параметров Ψ и ϕ0 формула может быть преобразована к виду Структура АМК с однотональной модуляцией изображена на рис. 2.4. 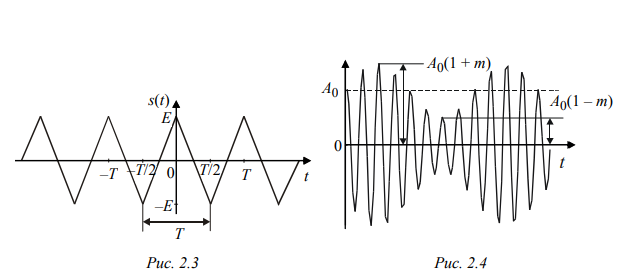 Колебание с однотональной угловой модуляцией (УМ) s5(t) в общем случае описывается таким образом: где β – индекс УМ, а остальные обозначения имеют тот же смысл, что и в формуле (2.6). В случае УМ (частотной или фазовой) с малой глубиной (β << 1) выражение (2.8) при нулевых значениях начальных фаз Ψ и ϕ0 может быть представлено в следующей форме: 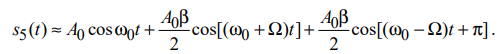 Если же условие малости глубины модуляции не выполняется, то колебание с однотональной УМ может быть разложено в бесконечный ряд: Колебание с однотональной УМ (2.8) изображено на рис. 2.5. Периодическая последовательность δ-функций s6(t), широко используемых в теоретической радиотехнике, представлена на рис. 2.6. 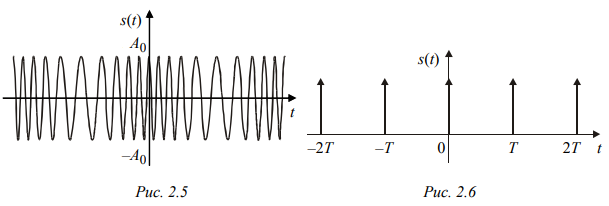 Обработка результатов Синтезированные сигналы: Последовательность прямоугольных импульсов 1 гармоника 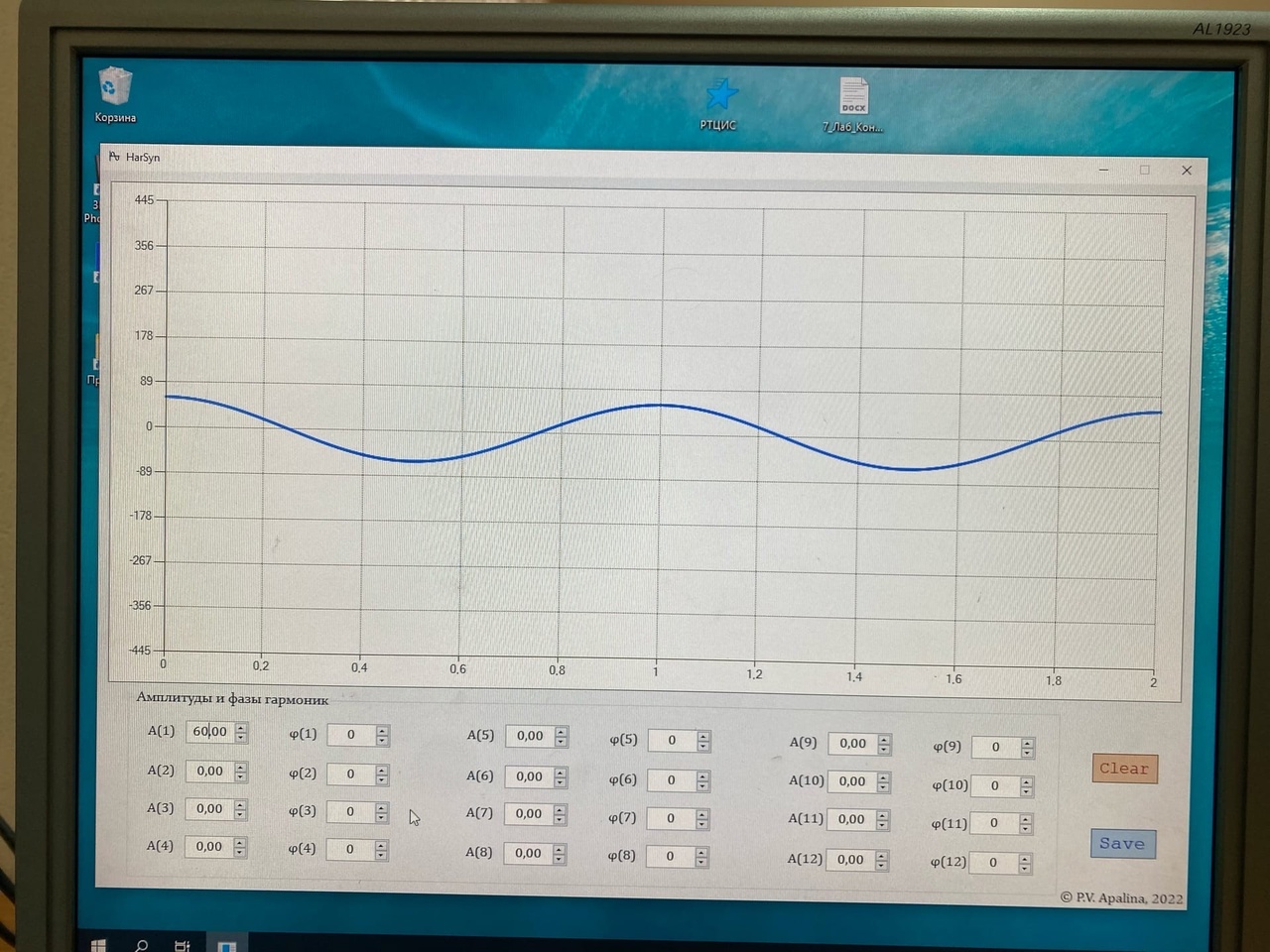 3 гармоника 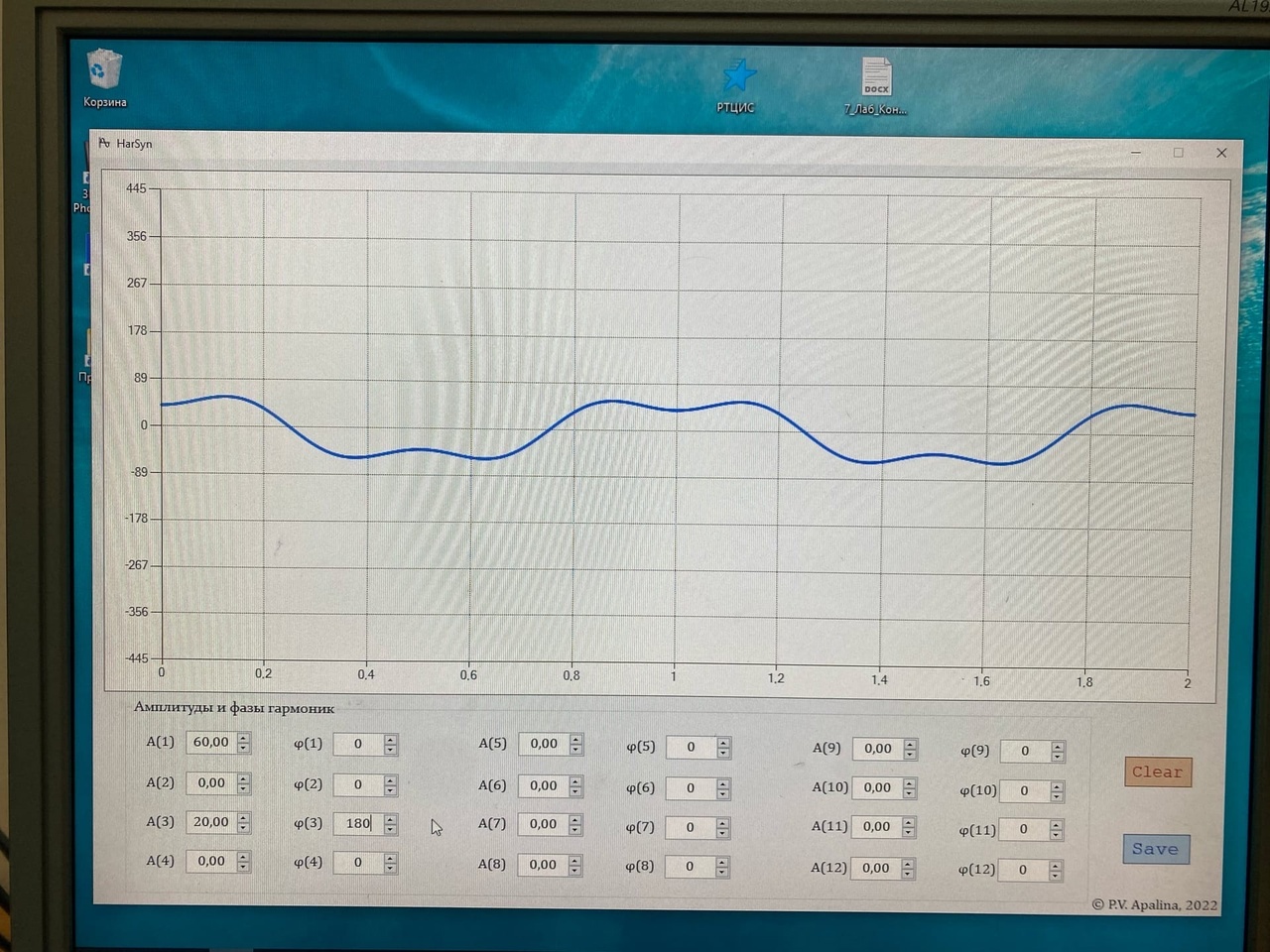 5 гармоника 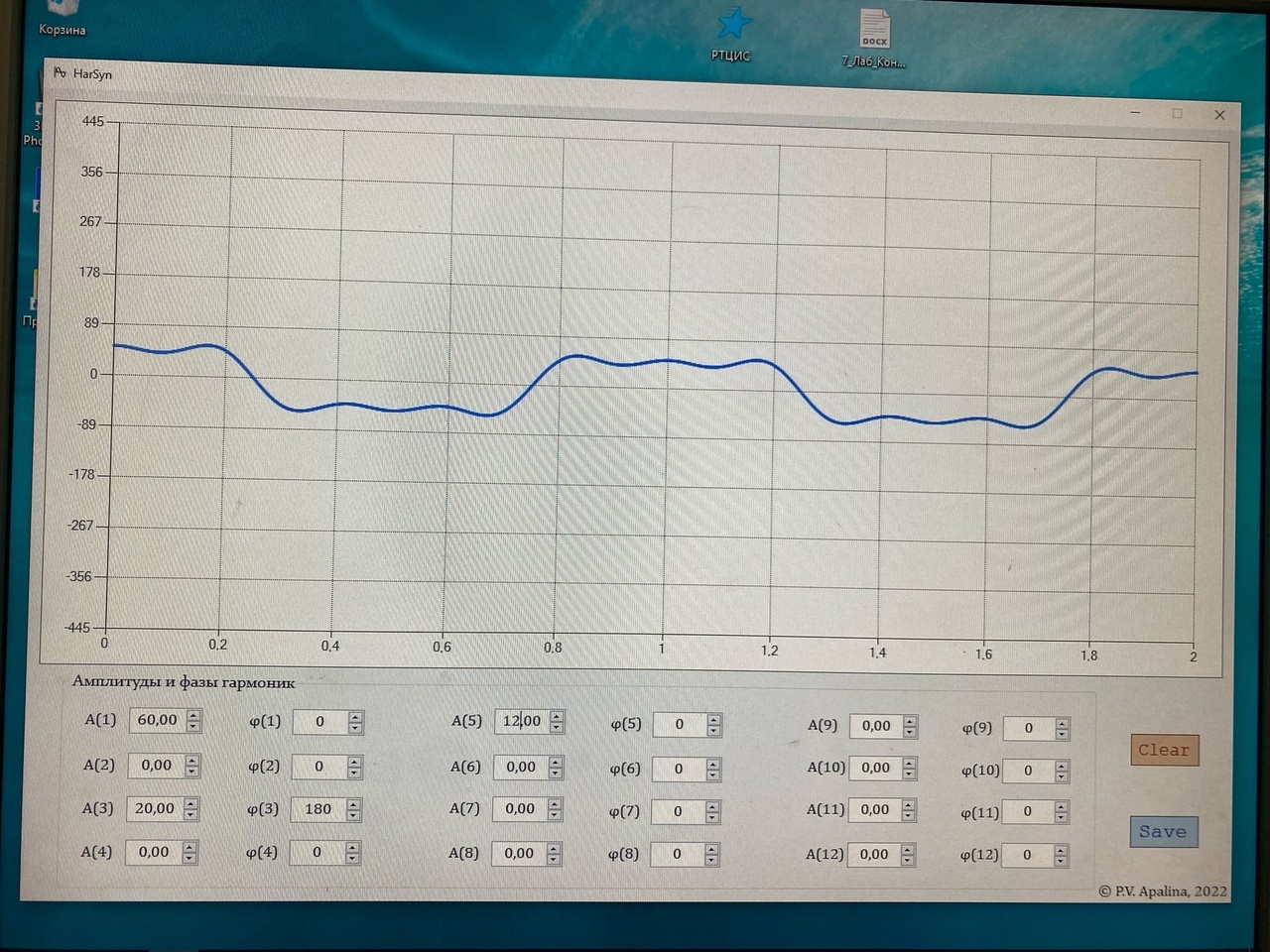 7 гармоника 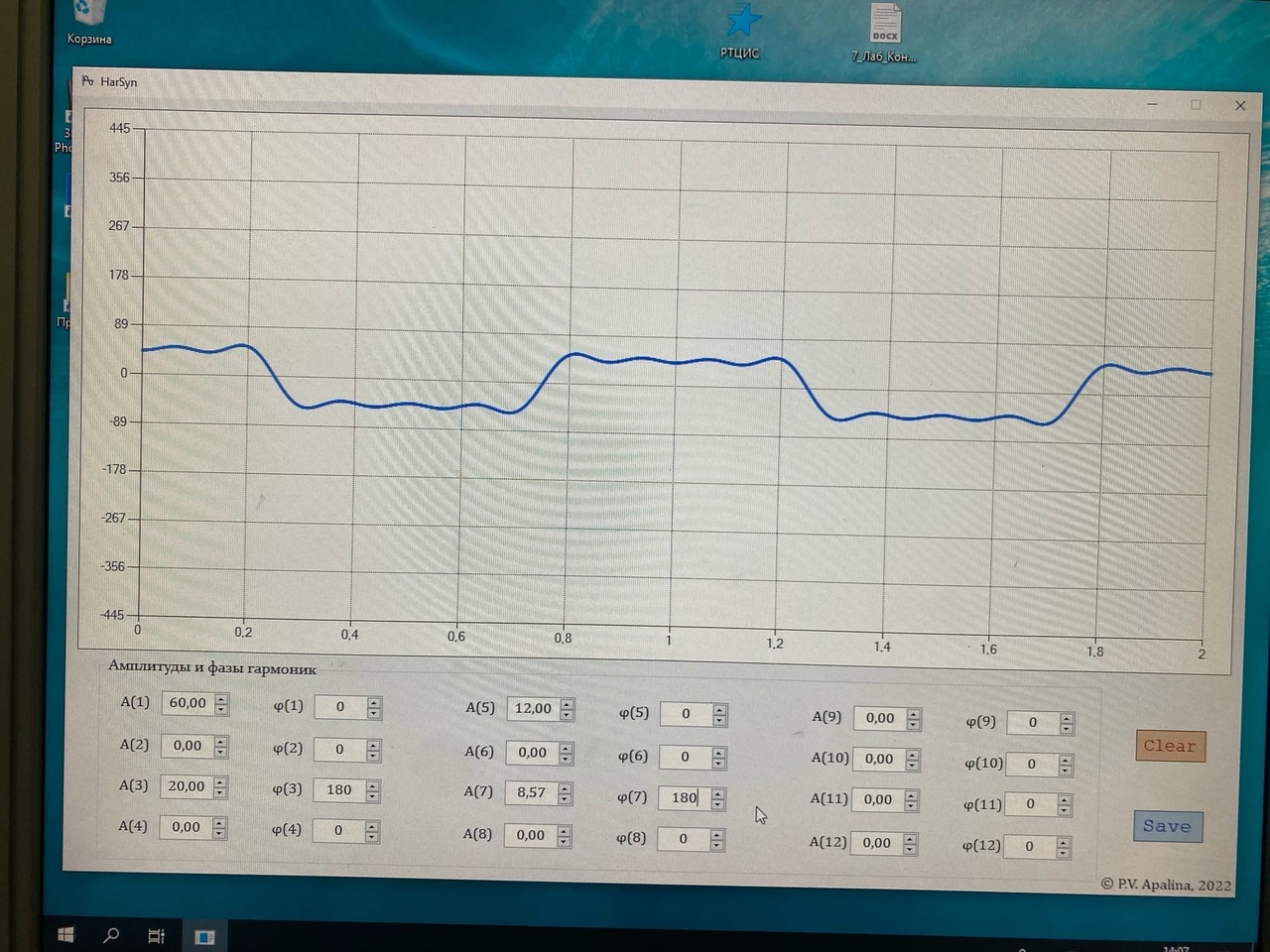 9 гармоника 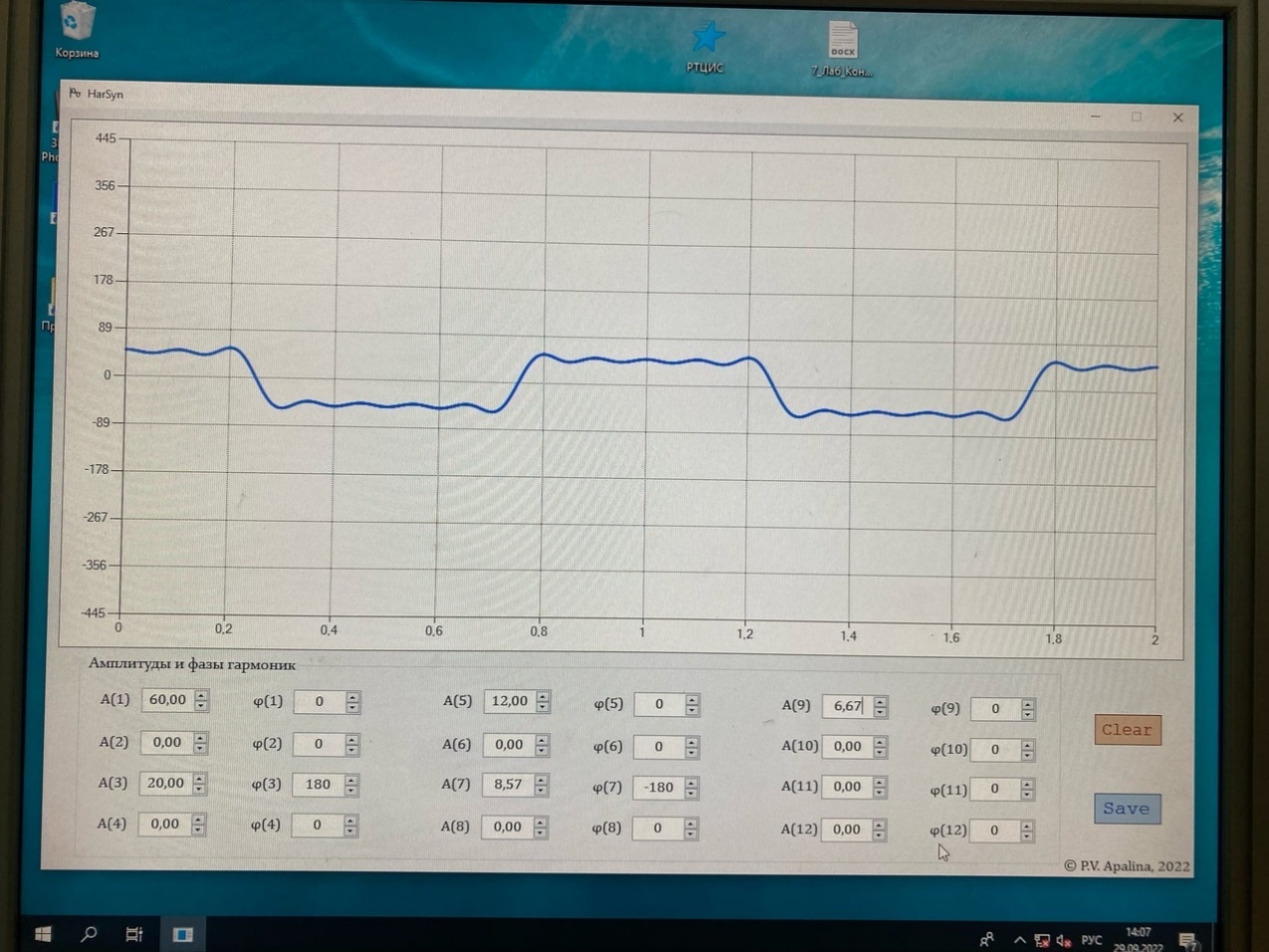 11 гармоника 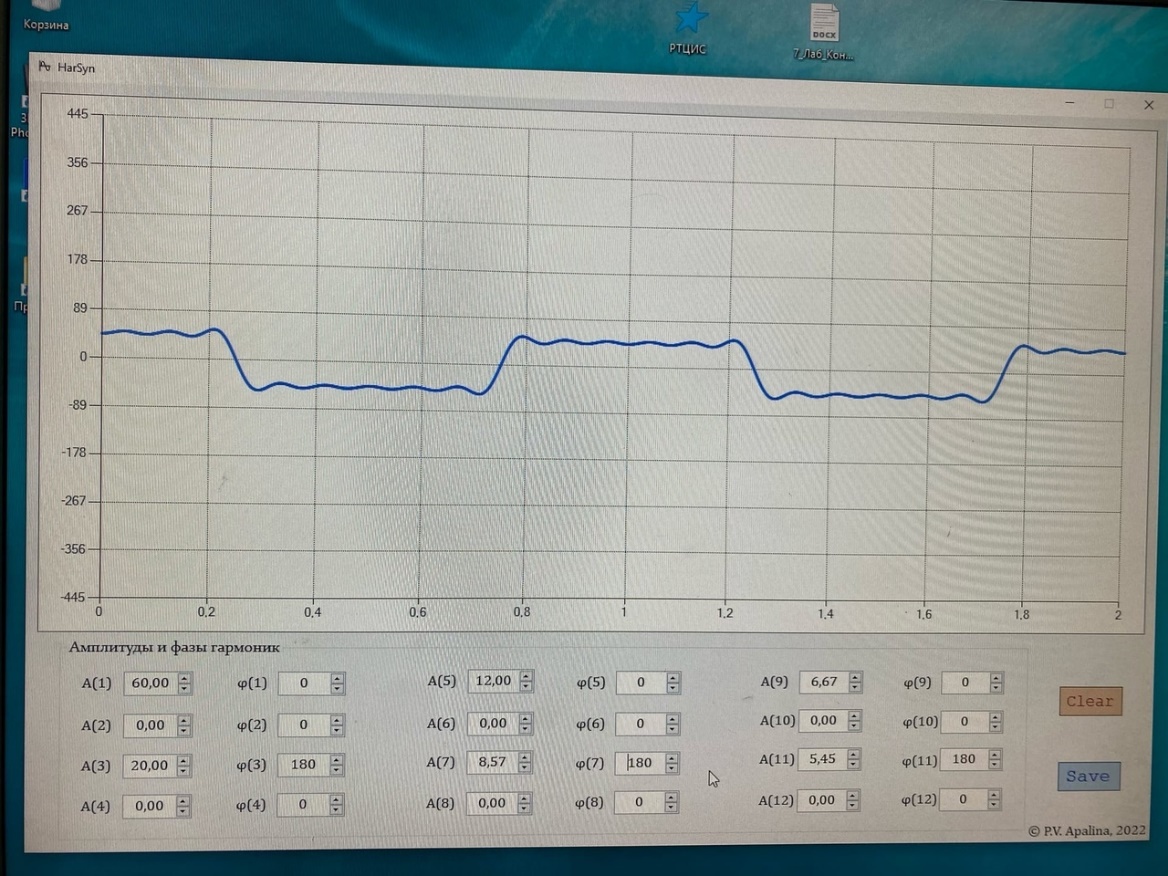 Амплитудный и фазовый спектры сигнала: 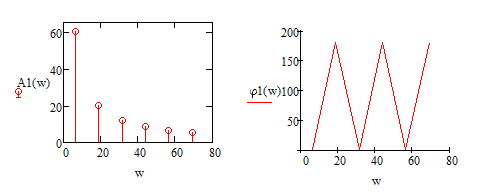 Последовательность пилообразных импульсов 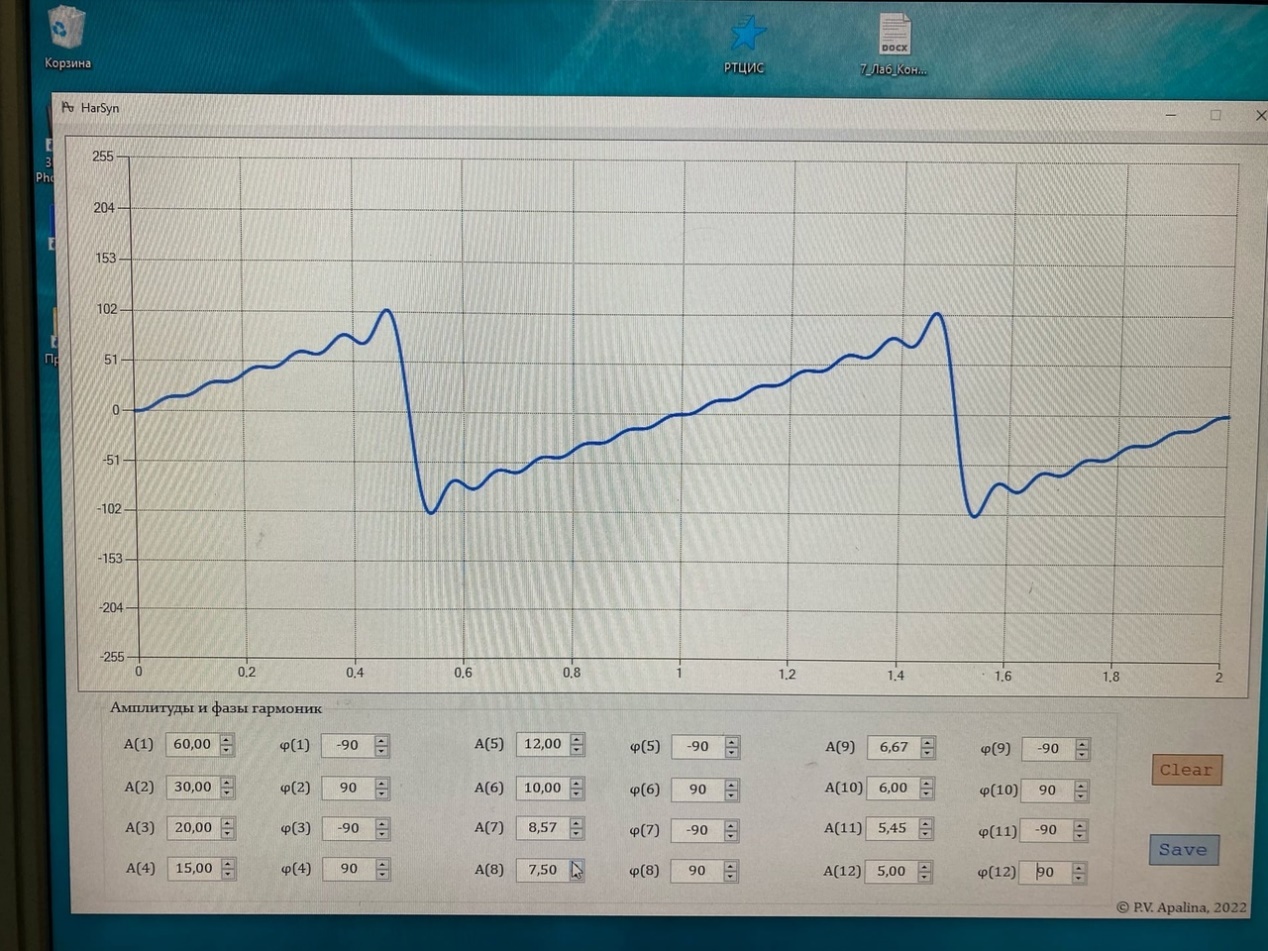 Амплитудный и фазовый спектры пилообразного сигнала: 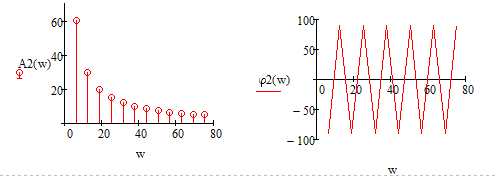 Последовательность треугольных импульсов 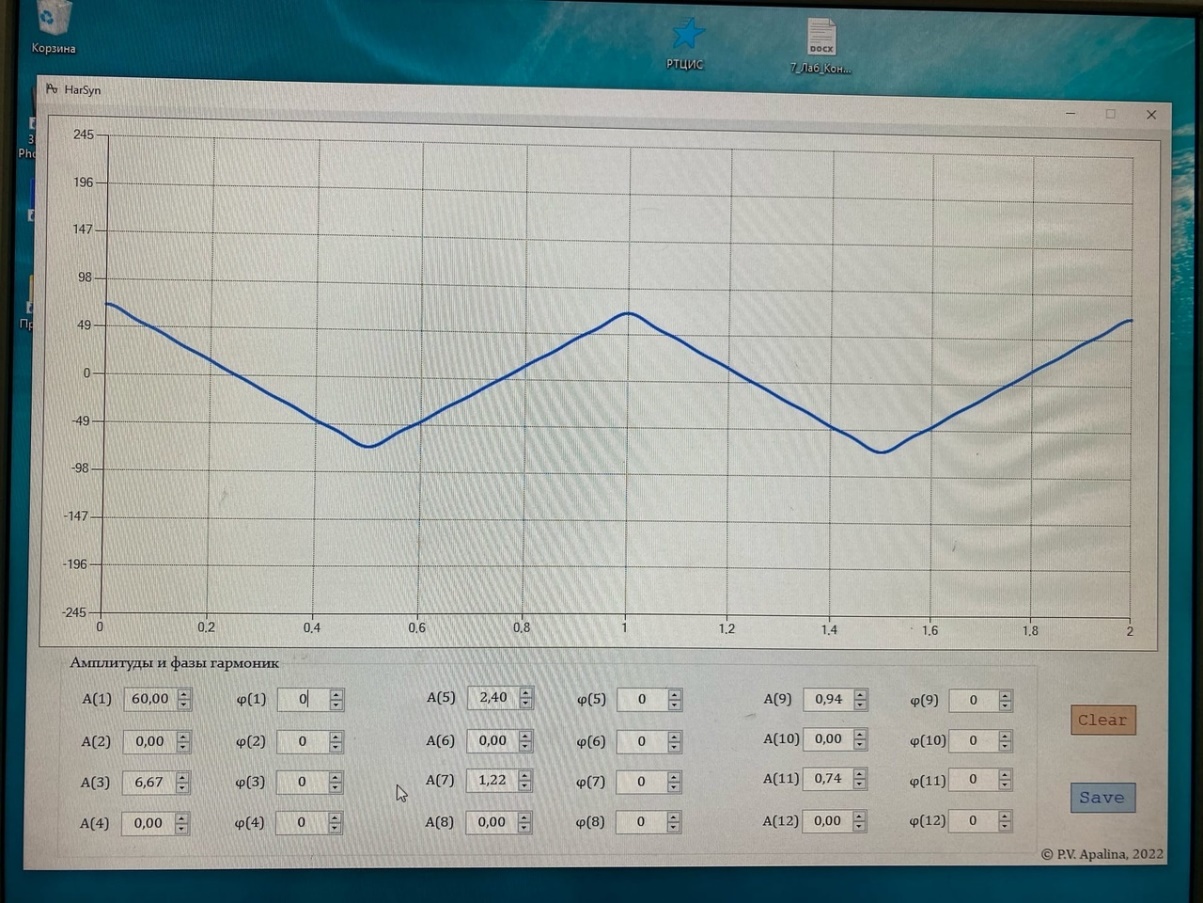 Амплитудный и фазовый спектры треугольного сигнала:  Сигнал с гармонической АМ m=0,5 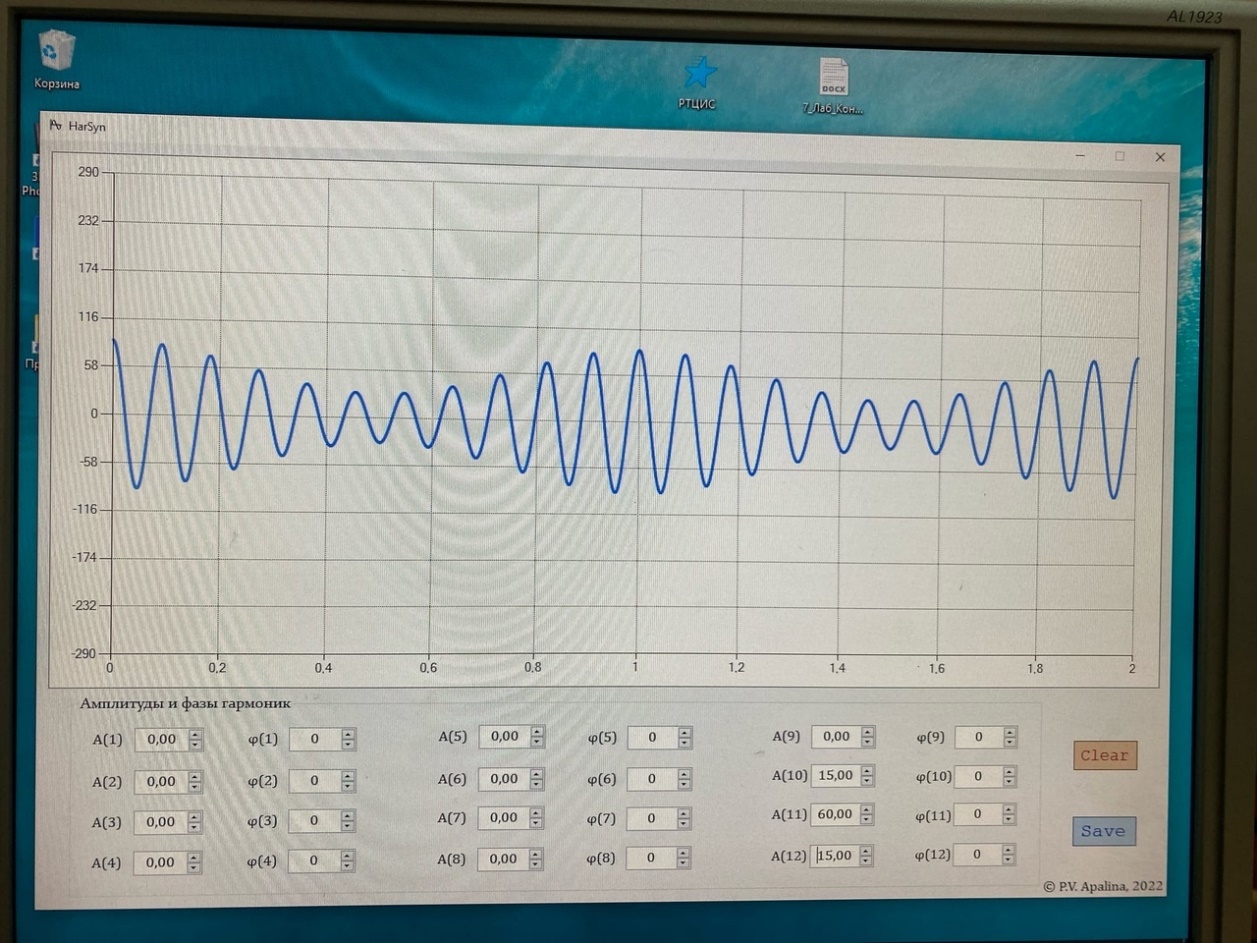 m=1 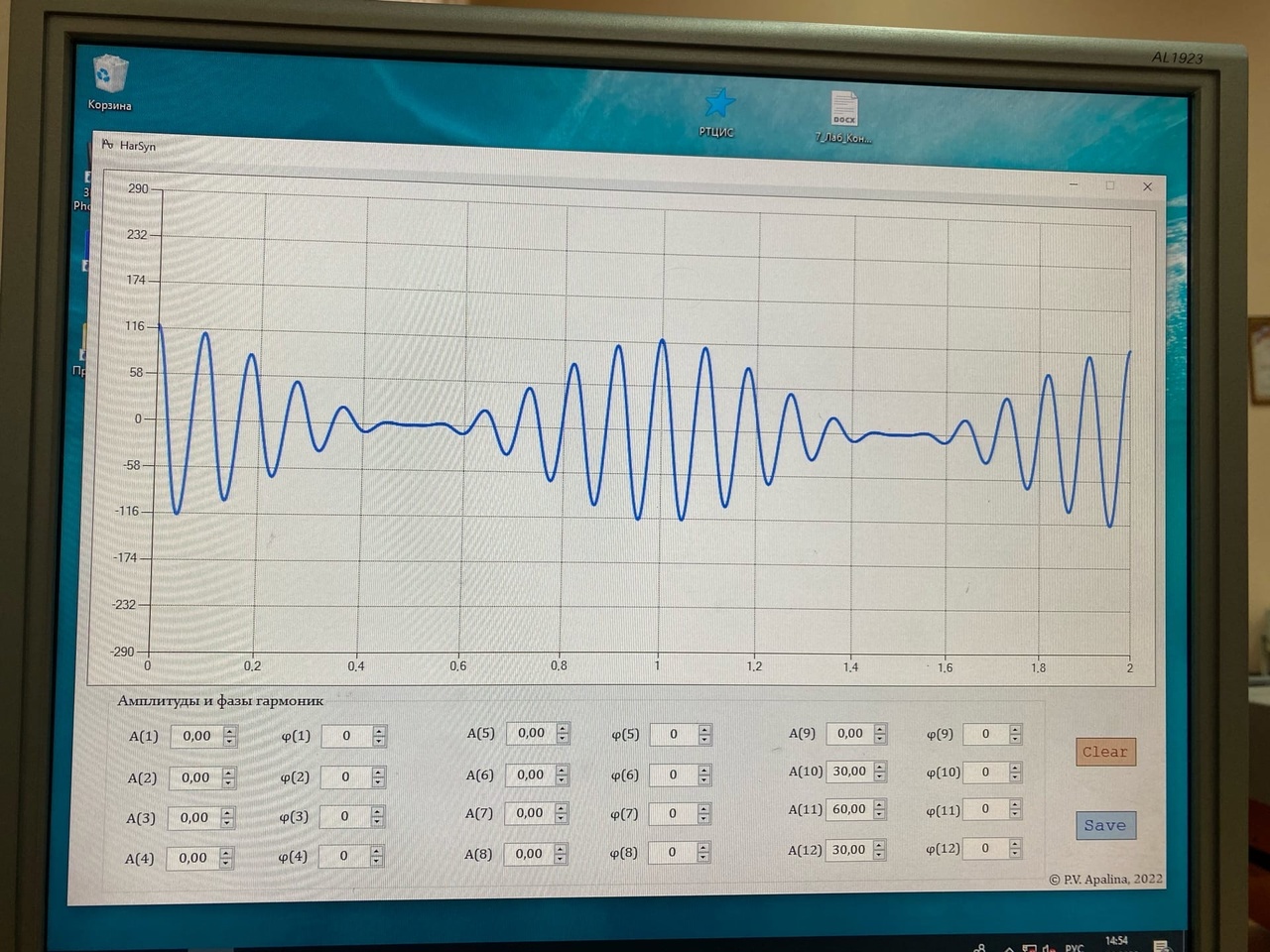 Сигнал с гармонической УМ β = 0,2 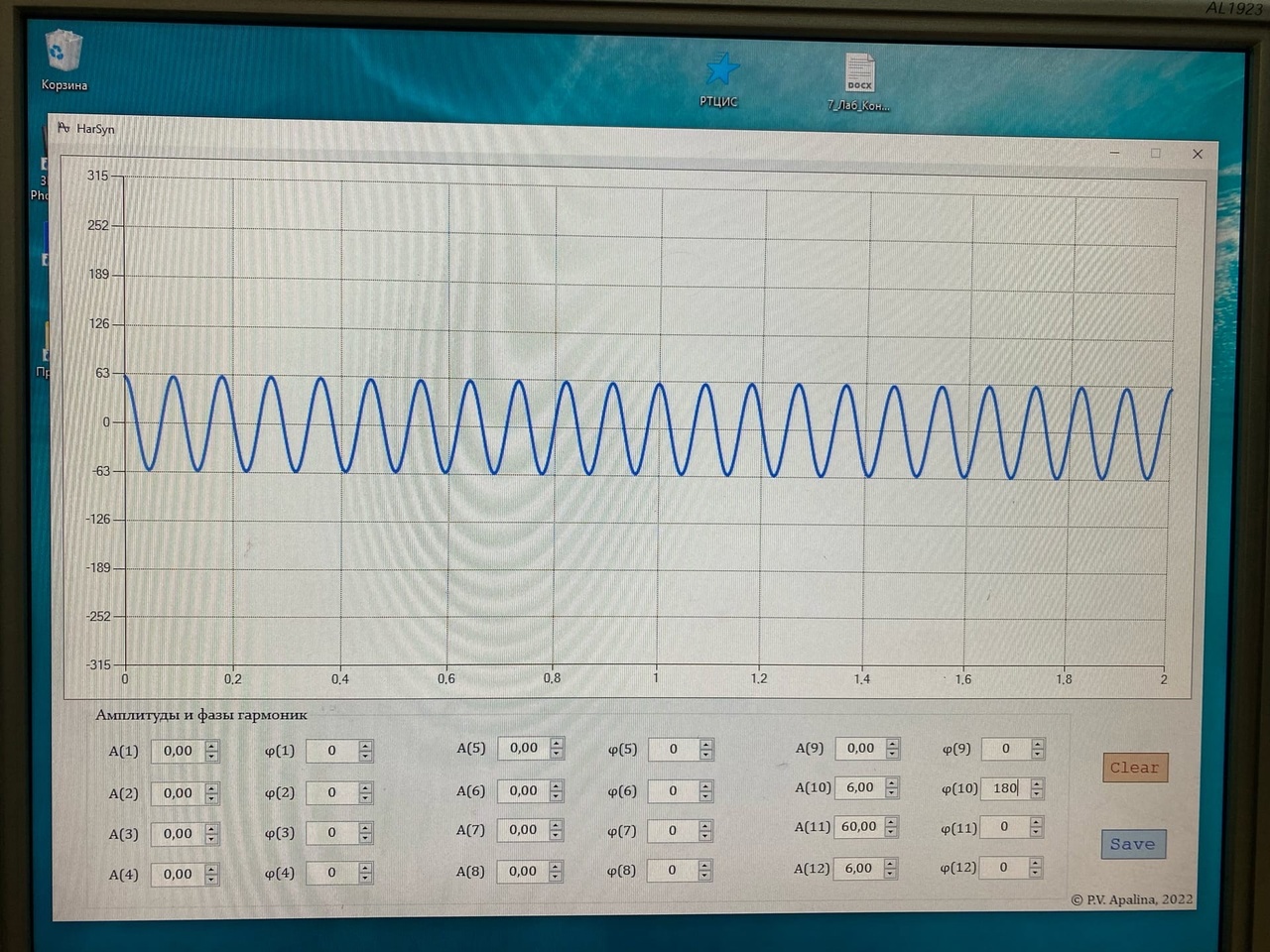 β = 2,4048 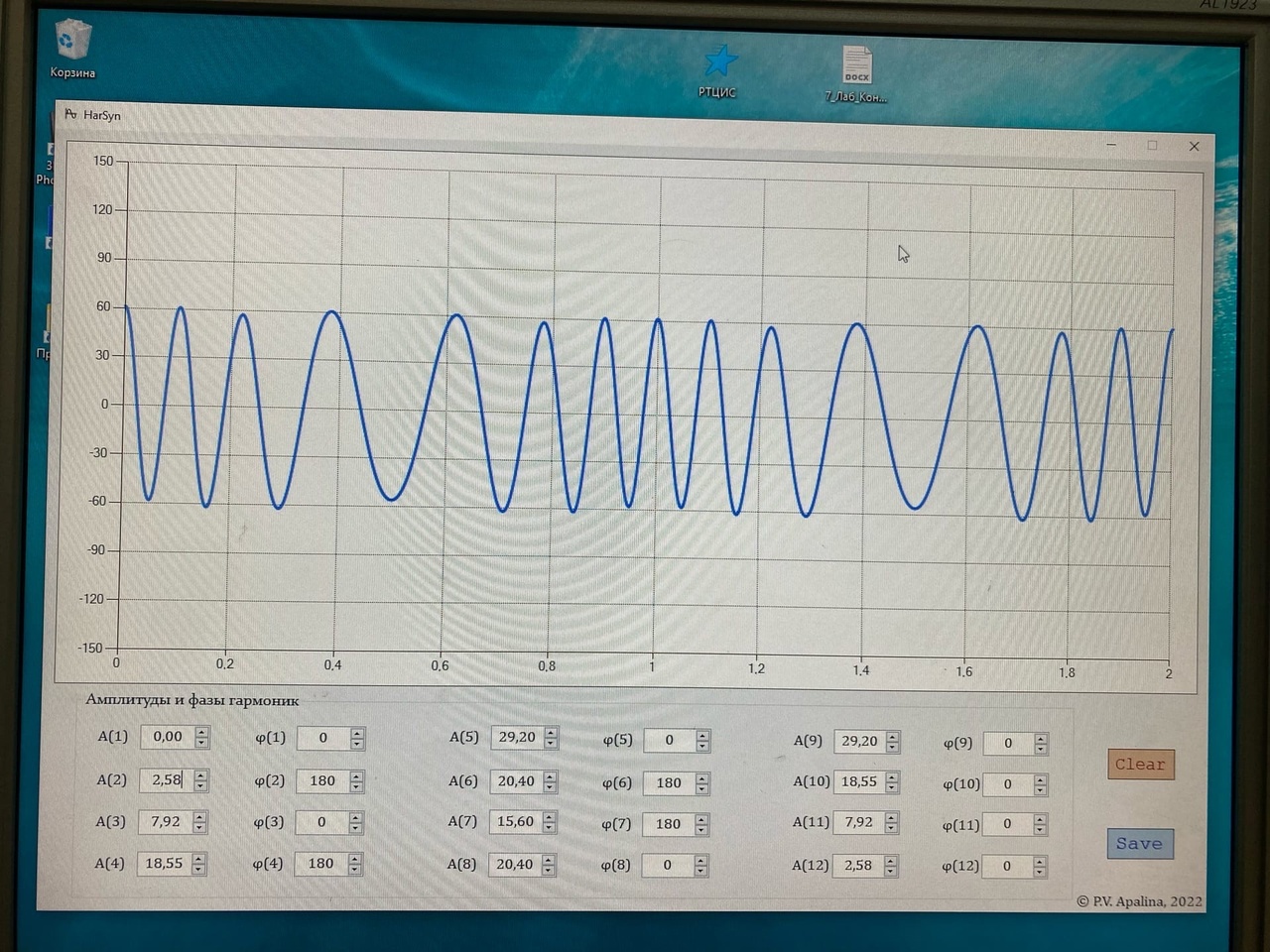 Периодическая последовательность δ-функций 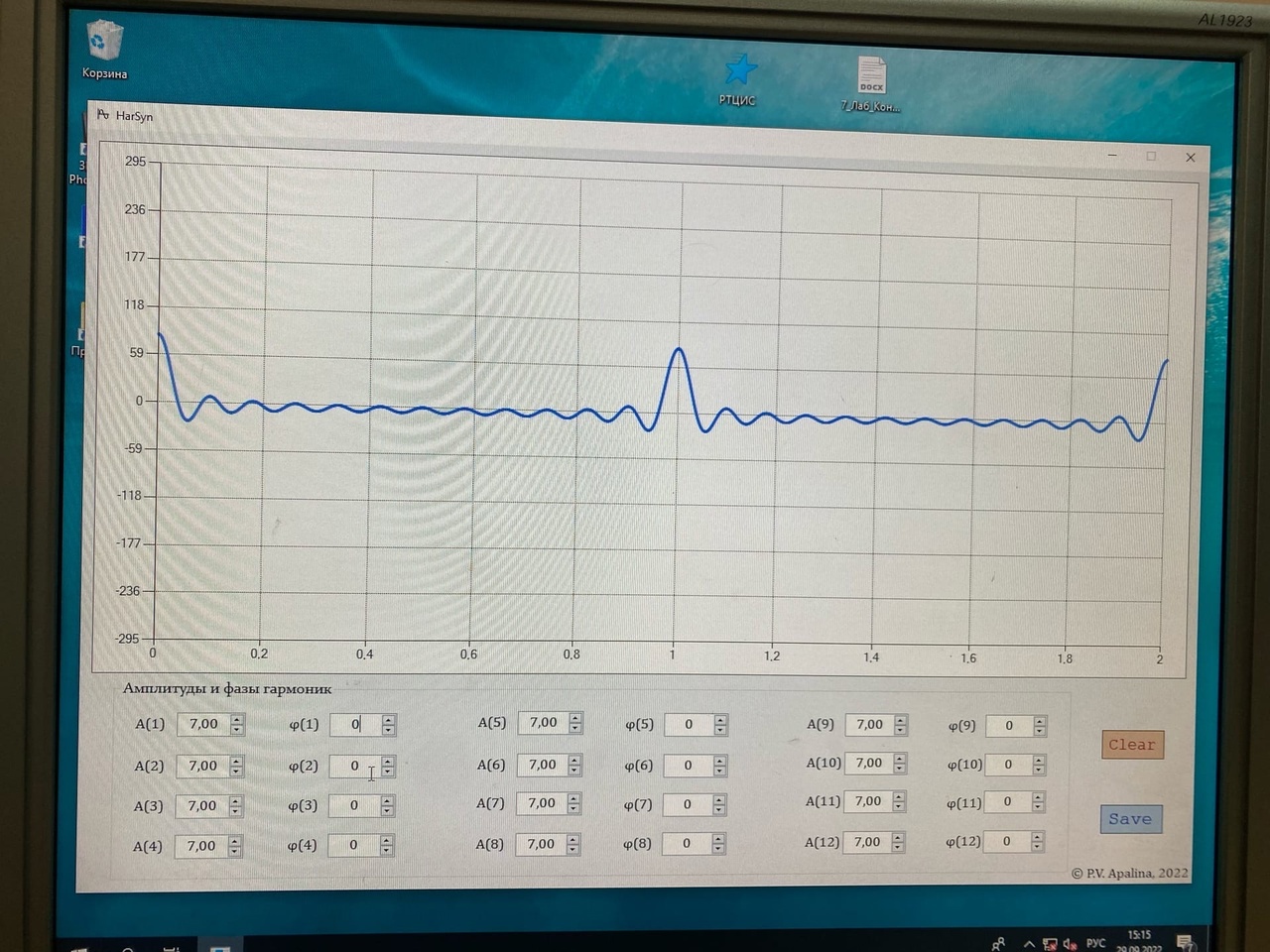 |
