Задания для для РГР 2 ТВ 2022 3. Задания для ргр 2 Теория вероятностей

• Название: Задания для ргр 2 Теория вероятностей
• Дата: 05.09.2022
• Размер: 113.14 Kb.
• Имя файла: Задания для для РГР 2 ТВ 2022 3.docx
• Тип: Документы; #662467
• страница: 1 из 3

Задания для РГР № 2 Теория вероятностей

Вариант 1

1. Из 10 рабочих первой бригады четверо имеют пятый разряд, а остальные – четвертый. Из 15 рабочих второй бригады трое имеют пятый разряд, а остальные – четвертый. Из каждой бригады наугад выбирают по одному рабочему. Найти вероятность того, что они оба имеют пятый разряд.

2. Производится посев семян пшеницы 4 сортов. При этом зерна 1 сорта составляют 15% от общего количества, второго сорта – 10%, третьего сорта – 20%, а остальные – четвертого сорта. Вероятность того, что из зерна вырастет колос, содержащий не менее 30 зерен для пшеницы первого сорта, составляет 25%, для пшеницы второго сорта – 40%, для третьего сорта – 8%, для четвертого сорта – 4%. Найти вероятность того, что из взятого наугад зерна вырастет колос, содержащий не менее 30 зерен.

3. Достигшему 71 год человеку вероятность заболеть во время эпидемии гриппа равна 0,07. Какова в этих условиях вероятность, что из 4 человек заболеют 2 человека данного возраста.

4. Преподаватель задает студенту дополнительные вопросы и прекращает задавать вопросы, как только студент не отвечает на вопрос. Всего преподаватель может задать не более трёх вопросов. Составить закон распределения случайной величины X – числа дополнительных вопросов, которые задаст преподаватель, если вероятность того, что студент ответит на дополнительный вопрос, равна 0,8. Найти математическое ожидание и дисперсию этой случайной величины.

5. Случайная величина X задана функцией распределения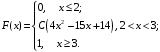



Вычислить C, М(X), D(X), σ(Х). Найти вероятность P(2,5 < X< 3,25). Построить графики плотности f(x)и функции распределения F(x).

6. Случайная величина Xраспределена равномерно на отрезке [–1; 3]. Найти ее дисперсию и вероятность попадания X в интервал [–1/2; 1/2].

7. Случайная величина X распределена по нормальному закону. Её математическое ожидание и дисперсия соответственно равны M(X) = 10,D(X) = 16. Найти вероятность попадания X в интервал (2; 13).

8. Длительность времени безошибочной работы сотрудника банка в течение рабочего дня имеет показательное распределение с параметром l = 0,2. Найти вероятность того, что за время рабочего дня (t = 8 часов): а) сотрудник сделает ошибку; б) сотрудник не сделает ошибку.
Вариант 2

1. Производится два выстрела по одной мишени. Вероятность попадания при первом выстреле равна 0,6, при втором – 0,7. Найти вероятность того, что будет ровно одно попадание.

2. В сборочный цех завода поступили детали с 3-х автоматов. Первый автомат дает 5% брака, второй – 2%, а третий – 3%. Определить вероятность попадания на сборку бракованной детали, если в цех поступило 400 деталей от первого автомата, 200 со второго и 400 от третьего.

3. В лотерее на каждые 1000 билетов приходится 25 выигрышей. Некто приобрел 3 билета. Найти вероятность того, что из трех купленных билетов один билет выигрышный.

4. Торговый агент имеет пять номеров потенциальных покупателей и обзванивает их по одному разу до тех пор, пока не получит заказ на покупку товара. Вероятность того, что потенциальный покупатель сделает заказ, равна 0,4. Составить закон распределения числа телефонных разговоров, которые предстоит провести агенту. Найти математическое ожидание и дисперсию этой случайной величины.

5. Случайная величина X задана функцией распределения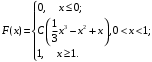



Вычислить C, М(X), D(X), σ(Х). Найти вероятность P(– 0,2 < X< 0,6). Построить графики плотности f(x)и функции распределения F(x).

6. Случайная величина X распределена равномерно на отрезке [–1; 4]. Записать её функцию распределения, найти вероятность попадания случайной величины в интервал (0; 2).

7. Расчёт себестоимости некоторого сложного изделия производится без систематических ошибок, т.е. среднее значение ошибки равно 0. Случайные ошибки расчёта подчинены нормальному распределению со средним квадратическим отклонением s = 15 у. е. Найти вероятность того, что расчет себестоимости будет произведён с ошибкой, не превосходящей по абсолютной величине 10 у. е.

8. Случайная непрерывная величина X распределена по показательному закону с параметром l = 0,2. Найти вероятность того, что в результате испытания Xпримет значение больше 4.


Вариант 3

1. В первом ящике 10 деталей, из них 7 стандартных. Во втором ящике 20 деталей, из них 12 стандартных. Из каждого ящика наугад взяли по одной детали. Найти вероятность того, что они обе стандартные.

2. Прибор может собираться из деталей двух типов. Из деталей первого типа собирается 40% приборов. Для них надежность (надежность – вероятность безотказной работы) прибора равна 0,95. Для деталей второго типа надежность составляет 0,7. Прибор работал безотказно. Найти вероятность того, что он собран из деталей первого типа.

3. Из 1000 человек 1 группу крови имеют 400 человек. Найти вероятность того, что из случайно выбранных пяти человек имеют 1 группу крови 3 человека.

4. Абонент, забыв последнюю цифру телефонного номера, набирает её наугад. Записать закон распределения случайной величины X – количества наборов номеров до угадывания. Найти математическое ожидание и дисперсию этой случайной величины.

5. Непрерывная случайная величина X задана функцией распределения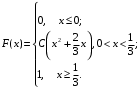



Вычислить C, М(X), D(X), σ(Х). Найти вероятность P(– 0,1 < X< 1/6). Построить графики плотности f(x)и функции распределения F(x).

6. Величина годовой прибыли некоторого предприятия распределена равномерно на отрезке [5; 15] млн. у. е. Каковы математическое ожидание и дисперсия годовой прибыли этого предприятия?

7. Случайная величина Xраспределена нормально с M(X) = 1, D(X) = 0,25. Найти, на какую величину значения случайной величины X отличаются от математического ожидания с вероятностью 0,997.

8. Случайная величина X распределена по показательному закону с параметром l = 1/3. Что вероятнее: в результате испытания X окажется меньше 2 или больше 2?

Вариант 4

1. Из 20 студентов первой группы 6 отличников, а из 21 студента второй группы – 7. Из каждой группы наугад взяли по одному студенту. Найти вероятность того, что точно один из них отличник.

2. Прибор может работать в нормальном и перегруженном режимах работы. Нормальный режим наблюдается в 80% случаев, при этом вероятность выхода прибора из строя равна 10%, а в перегруженном – 60%. Найти вероятность выхода прибора из строя.

3. В среднем 30% акций продаются на аукционе по первоначальной цене. Найти вероятность того, что из десяти пакетов акций в результате торгов будут проданы 4 пакета по первоначальной цене.

4. Сделано два высокорисковых вклада: 10 тыс. у. е. в компанию A и 15 тыс. у. е. в компанию B. Компания A обещает 50 % годовых, но может полностью разориться с вероятностью 0,2. Компания B обещает 40 % годовых, но может полностью разориться с вероятностью 0,15. Получение прибыли от каждой из компаний считать независимыми событиями. Составить закон распределения случайной величины X – общей суммы прибыли, полученной от двух компаний, найти ее математическое ожидание и дисперсию.

^{5. Случайная величина X задана функцией распределения}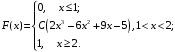



Вычислить C, М(X), D(X), σ(Х). Найти вероятность P(1,5 < X< 2,3). Построить графики плотности f(x)и функции распределения F(x).

6. Случайная величина X распределена равномерно на отрезке [–0,5; 2,5]. Найти M(X) и D(X). Что вероятнее: в результате испытания X окажется в интервале [0; 1] или вне этого интервала.

7. Случайная величина X распределена по нормальному закону с M(X) = –1,D(X) = 0,25. Найти интервал, симметричный относительно математического ожидания, которому принадлежат значения случайной величины Xс вероятностью 0,997.

8. Тупиковая станция обслуживает потребности предприятия, но принимает и грузы для других потребителей. Число таких вагонов, прибывающих в течение суток, является случайной величиной, распределенной по показательному закону с параметром l = 0,05. Определить вероятность прибытия на эту станцию в течение суток от 20 до 30 вагонов других потребителей.

Вариант 5

1. Для сигнализации установлены два независимо работающих сигнализатора. Вероятность того, что сработает первый сигнализатор, равна 0,9, а второй – 0,85. Найти вероятность того, что сработает только один сигнализатор.

2. Абитуриент может сдавать вступительный экзамен любому из трех преподавателей. Вероятность сдать экзамен первому составляет 0,45, а остальным по 0,3. Абитуриент случайным образом выбрал экзаменатора и сдал экзамен. Какова вероятность того, что абитуриент сдавал экзамен первому экзаменатору.

3. Вероятность сбоя в работе телефонной станции при каждом вызове в праздники равна 0,004. Поступило 1000 вызовов. Определить вероятность того, что было 5 сбоев.

4. Тест состоит из пяти вопросов, на каждый из которых приведено четыре варианта ответа, из которых только один правильный. Студент не знает ни одного вопроса и выбирает ответы наудачу. Составить закон распределения случайной величины X – числа правильно угаданных ответов теста. Найти ее математическое ожидание и дисперсию.

5. Случайная величина X задана функцией распределения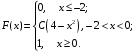



Вычислить C, М(X), D(X), σ(Х). Найти вероятность P(– 1 < X< 0,5). Построить графики плотности f(x)и функции распределения F(x).

6. Случайная величина X распределена равномерно на отрезке [–0,1; 5,3]. Найти вероятность попадания случайной величины X в интервал [3; 4].

7. Стоимость акции предприятия на рынке подчиняется нормальному закону распределения. Её средняя стоимость равна 50 у. е., а среднее квадратичное отклонение равно 1 у. е. Найти вероятность того, что удастся приобрести акцию предприятия по цене не меньше 49,5 у. е. и не больше 50,5 у. е.

8. Непрерывная случайная непрерывная величина X распределена по показательному закону с параметром l = 2. Найти вероятность попадания X в интервал (0; 3).

Вариант 6

1. Причиной разрыва электрической цепи служит выход из строя хотя бы одного элемента. Элементы могут выйти из строя с вероятностью 0,2; 0,4; 0,5. Какова вероятность разрыва электрической цепи.

2. На территории района работают три страховых агента независимо друг от друга. Вероятность выбора первого агента равна 0,2, второго –0,5, а третьего – 0,3. Известны вероятности вежливого и своевременного обслуживания клиентов: для первого агента она равна 0,1, для второго – 0,5 и для третьего – 0,7. Клиент был обслужен вовремя и вежливо. Какова вероятность того, что он обслужен вторым агентом.

3. Вероятность рождения мальчика равна 0,515. Найти вероятность того, что среди 12 новорожденных будет 9 девочек.

4. Монету бросают шесть раз. Записать закон распределения случайной величины X – числа выпадений герба. Найти математическое ожидание M(X) и дисперсию D(X).

5. Случайная величина X задана функцией распределения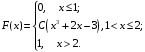



Вычислить C, М(X), D(X), σ(Х). Найти вероятность P(0,8 < X< 3/2). Построить графики плотности f(x)и функции распределения F(x).

6. Толщина конспекта по математике студента распределена равномерно от 10 до 50 листов. Какова вероятность обнаружить конспект по математике толщиной от 40 до 45 листов?

7. Случайная величина X распределена по нормальному закону с M(X) = 9,D(X) = 25.Записать её плотность распределения, найти вероятность попадания X в интервал (5; 14).

8. Случайная величина X распределена по показательному закону с параметром l = 0,5. Какова вероятность, что в результате испытания X примет значение больше 1?

Вариант 7

1. Покупатель приобрел две лампы. Вероятность того, что лампа не выйдет из строя для первой равна 0,9, а для второй – 0,8. Найти вероятность того, что обе лампы не выйдут из строя.

2. В налоговую инспекцию поданы 15 деклараций, для которых вероятность правильного оформления равна 0,8 и 10 деклараций – с вероятностью правильного оформления 0,9. Найти вероятность того, что взятая наудачу декларация правильно оформлена.

3. Вероятность победы спортсмена в матче равна 0,7. Какова вероятность того, что в 6 поединках он победит 4 раза.

4. Предприниматель обещает поставить товар по цене 50 у. е. за единицу в случае предоплаты. В случае расчетов после получения товар будет стоить дороже. Известно, что 30 % клиентов этого предпринимателя предпочитают предоплату, а в среднем товар продается по цене 78 у. е. за единицу. Определить, по какой стоимости предприниматель продает свой товар при оплате после получения. Составить закон распределения случайной величины X – стоимости единицы товара. Найти дисперсию этой случайной величины.

5. Случайная величина X задана функцией распределения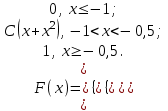



Вычислить C, М(X), D(X), σ(Х). Найти вероятность P(0,8 < X< 3/2). Построить графики плотности f(x)и функции распределения F(x).

6. Случайная величина Xраспределена равномерно на отрезке [–2; 4]. Найти её дисперсию и вероятность попадания X в интервал [–1/2; 1/2].

7. Случайная величина X распределена по нормальному закону. Её математическое ожидание и дисперсия соответственно равны M(X) = 5,D(X) = 9. Найти вероятность попадания X в интервал (0;10).

8. Секретарь совершает в среднем одну ошибку за 3 часа. Время работы до совершения ошибки имеет показательное распределение. Найти вероятность того, что за время рабочего дня (t = 8 часов) секретарь ни разу не ошибётся.

Вариант 8

1. Вероятность того, что рабочий перевыполнит план равна 0,7, а вероятность того, что в случае перевыполнения плана он не получит премию равна 0,2. Какова вероятность того, что рабочий получит премию.

2. Преподаватель проверяет контрольную работу трех групп студентов. В первой группе 10% студентов написали контрольную работу на неудовлетворительную оценку, во второй – 20%, а в третьей – 15%. Найти вероятность того, что взятая наугад работа имеет неудовлетворительную отметку, если в первой группе 18 студентов, во второй 20, а в третьей – 25.

3. Теннисист завершает вничью в среднем 25% партий. Определить вероятность завершить вничью 4 партии в турнире из 12 партий.

4. Игральную кость бросают три раза. Построить закон распределения случайной величины X – числа выпадений шестерки. Найти математическое ожидание M(X)и дисперсию D(X).

5. Случайная величина X распределена с плотностью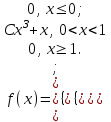



Вычислить C, М(X), D(X), σ(Х), F(x). Найти вероятность P(0,8 < X< 3/2). Построить графики плотности f(x)и функции распределения F(x).

6. Случайная величина X распределена равномерно на отрезке [–2,3; 4,0]. Найти вероятность попадания случайной величины X в интервал [3; 4].

7. Производится расчёт издержек при производстве некоторого изделия. Случайные ошибки расчета подчинены нормальному распределению с нулевым средним значением и средним квадратическим отклонением s = 10 у. е. Найти вероятность того, что расчёт себестоимости будет произведён с ошибкой, не превосходящей по абсолютной величине 15 у. е.

8. Непрерывная случайная величина X распределена по показательному закону с параметром l = 0,5. Найти вероятность того, что в результате испытания Xпопадает в интервал (1; 2).


Вариант 9

1. Вероятность безотказной работы телевизора равна 0,7. Куплено 2 телевизора. Найти вероятность того, что хотя бы один из них потребует ремонта.

2. Учителями биологии могут работать выпускники двух вузов. Первый вуз выпускает 45% общего количества биологов, а второй – 55%. Из первого вуза идут работать в школу 40% выпускников, а из второго – 60%. Какова вероятность, что данный выпускник будет работать в школе биологом?

3. Вероятность получения дивидендов по акциям равна 0,25. Некто приобрел 10 акций. Какова вероятность, что покупатель получит дивиденды по шести из них?

4. На складе фирмы три партии различного товара А и В. Стоимость товара партии A составляет 50 000 руб., партии B – 30 000 руб. При реализации товара фирма не делит партии на части. Вероятность того, что партия A будет продана равна 0,5; партия B – 0,8. Составить закон распределения суммарной выручки фирмы. Найти математическое ожидание и дисперсию этой случайной величины.

5. Случайная величина X задана функцией распределения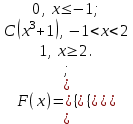



Вычислить C, М(X), D(X), σ(Х). Найти вероятность того, что X в результате испытания окажется в интервале (1/2; 3/2). Построить графики плотности f(x)и функции распределения F(x).

6. Величина годовой прибыли некоторого предприятия распределена равномерно на отрезке [1; 4] млн у. е. Каковы математическое ожидание и дисперсия годовой прибыли этого предприятия?

7. Случайная величина Xраспределена нормально с M(X) = 5, D(X) = 0,5. Найти интервал, симметричный относительно математического ожидания, которому принадлежат значения случайной величины Xс вероятностью 0,997.

8. Случайная величина X распределена по показательному закону с параметром l = 1/4. Что вероятнее: в результате испытания X окажется меньше 3 или больше 3?